人教版六年级下册数学小升初应用题综合复习 课件(共31张PPT)
文档属性
| 名称 | 人教版六年级下册数学小升初应用题综合复习 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 11:07:46 | ||
图片预览









文档简介
(共31张PPT)
应
用
题
综
合
小升初数学
公 式
简单工程问题:
三要素:
工作总量、工作效率、工作时间
若工作总量没有告诉具体的数量,
我们可以设工作总量为单位“1"。
知识小结
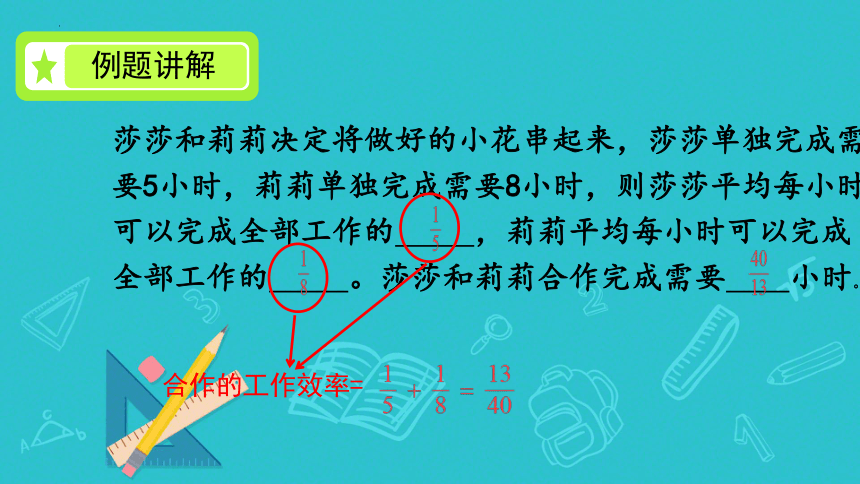
例题讲解
合作的工作效率=
莎莎和莉莉决定将做好的小花串起来,莎莎单独完成需要5小时,莉莉单独完成需要8小时,则莎莎平均每小时可以完成全部工作的 ,莉莉平均每小时可以完成全部工作的 。莎莎和莉莉合作完成需要 小时。
修一条公路,甲单独完成需要4天,乙单独完成需要12天。如果两人合作,需要 天完成。
知识探索
将整个工程看作单位“1”
甲的工作效率:1÷4 =
乙的工作效率:1÷12=
甲、乙合作的工作效率:
甲、乙合作的工作时间:1÷ = 3(天)
例题讲解
一项工程,甲队单独完成需10天,乙队单独完成需15天,可是甲、乙两队的时间不能统一,所以他们决定轮流完成,如果甲队先做4天,乙队再接着做,则乙队需 天能将这个工程完成。
9
分 工 与 合 作
小提示:分干合想,合干分想
例题讲解
一项工程,甲队单独完成需40天,若乙队先做10天,余下的工程由甲、乙两队合作,再干20天即可完成。如果乙队单独完成此工程,则需 天。
等量关系式
工作总量 = 甲的工作量 + 乙的工作量
合作20天的工作量
合作20天的工作量
单干10天的工作量
60
知识探索
玩具加工厂需要加工一批玩具,师父单独加工12天可以完成。现在师父和徒弟一起加工了7天,然后让徒弟一个人接着干3天完成了这批玩具的加工。那么,这批玩具由徒弟单独做需要 天才能完成。
24
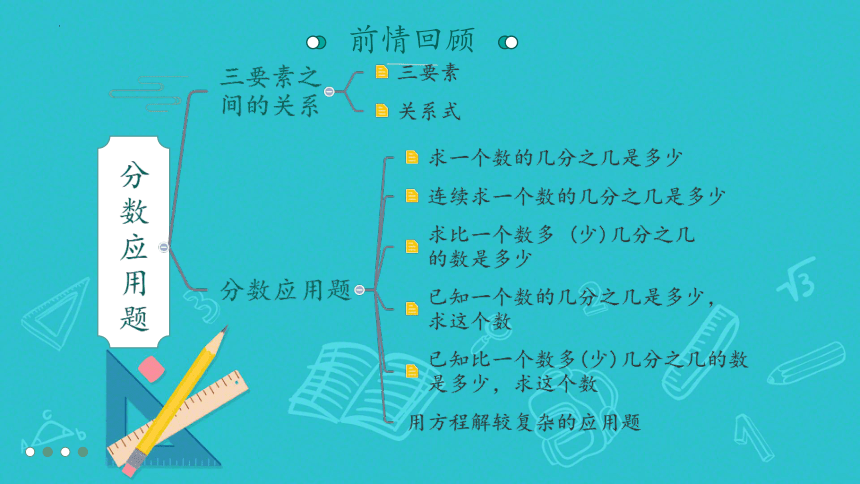
前情回顾
探索真相
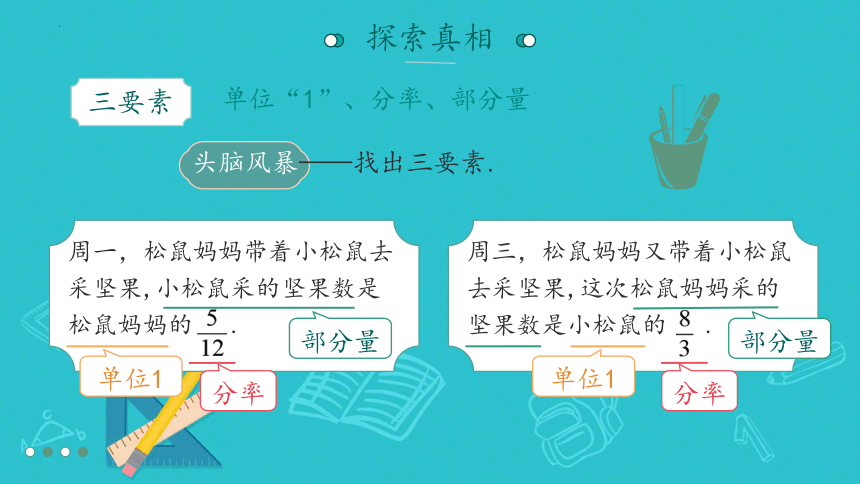
三要素
单位“1”、分率、部分量
头脑风暴——找出三要素.
周一,松鼠妈妈带着小松鼠去采坚果,小松鼠采的坚果数是松鼠妈妈的 .
周三,松鼠妈妈又带着小松鼠去采坚果,这次松鼠妈妈采的坚果数是小松鼠的 .
部分量
单位1
分率
部分量
单位1
分率
探索真相
会应用
分数应用题(只列式不计算)
某小学六年级学生报名参加兴趣小组,已知参加数学小组的有32人.
英语小组的人数是数学小组的 ,英语小组有_______人.
语文小组的人数比数学小组多 ,语文小组有___________人。
数学小组的人数是美术小组的 ,美术小组有______人.
数学小组的人数比音乐小组多 ,音乐小组有___________人.
探索真相
会应用
小高家附近新开了一家老北京糖葫芦店。店主做了一些糖葫芦,由于开业大酬宾,很快就卖出了 ,于是店主又做了38根,此时的糖葫芦比原来的还多 ,你知道店主原来做了多少根糖葫芦吗
量率对应
“38根”对应的分率是______.
单位“1”未知,用除法
单位“1”=部分量÷分率
两个部分量对应的单位“1”一样吗?
A.一样 B. 不一样
探索真相
过难关
小帅的妈妈买了苹果、香蕉、梨三种水果,共4000克,他发现苹果的质量是香蕉和梨的 ,香蕉的质量是苹果和梨的 。那么梨的质量占三种水果总量的几分之几?
想一想如何计算?
小帅灵机一动,说应该是 .
你觉得正确吗?
观察分析
单位“1”不统一,
分率不能直接相加减。
探索真相
过难关
单位“1”不统一,先统一单位“1”。
分析
将单位“1”统一为谁呢?
三种水果的总量。
苹果的质量是其余两种水果的 .
3份
5份
苹果的质量占总量的
香蕉的质量是其余两种水果的 .
香蕉的质量占总量的
梨的质量占三种水果总量的_______________.
2份
5份
3份
通过部分与整体统一单位“1”:遇到多个分率的单位“1”不统一时,先统一单位“1”.
总结
比的应用——利用不变量解决相关问题
甲、乙两个盒子中分别装有一些小球,它们的数量比是3:5.
分析下面每种情况,找准不变量,再连线。
连一连
会应用
比的应用——部分量不变
甲、乙两个盒子中分别装有一些小球,它们的数量比是3:5.再往甲盒中放入9个小球,数量比变为3:4. 原来甲、乙两个盒子中分别有多少个小球
思考:谁是不变量?
乙盒中的小球的数量是不变量.
甲 乙 统一后
原来 3 5 12 20
现在 3 4 15 20
=
=
:
:
:
:
1份:_____________(个);
原甲盒:__________(个);
原乙盒:__________(个).
9÷(15-12)=3
3x12=36
3x20=60
统一不变量的份数,关键是求1份量 ,再按比分配.
会应用
比的应用——和不变
甲、乙两个盒子中分别装有一些小球,它们的数量比是3:5. 从乙盒中拿出8个小球放入甲盒,数量比变为1:1,找到不变量统一份数.
思考:谁是不变量?
甲、乙两盒中小球的数量和是不变量.
对比分析
甲 乙 和
原来 3 5 8
现在 1 1 2
统一后 ×4 ×4 2×4=8
牛刀小试
练习
小爱养了红色、黄色、黑色三种颜色的小鱼,其中红色小鱼是其他两种小鱼总数的 ,黄色小鱼是其他两种小鱼总数的 .
红色小鱼是三种小鱼总数的________;
1
黄色小鱼是三种小鱼总数的________.
2
前情回顾
注意
设未知数的方法:
①直接设;②设单位“1”或1倍量;
③设容易表示其他量的为x.
列:根据等量关系列方程
探索真相
用字母表示数.
一站到底
A、B两袋面粉共400千克,吃了A袋面粉的40%.
设B袋面粉为x千克,那么吃了A袋面粉多少千克
40% ×(400-x)
400-40%x
探索真相
用字母表示数.
一站到底
某校六年级男生与女生人数相同,六年级女老师人数是男老师的2倍,且女老师与男生共128人.设六年级男老师有x人,那么女生有多少人
128-2x
128+2x
探索真相
用字母表示数.
一站到底
有一堆小球,每次取出6个,取了x次后,还剩10个小球那么原来这堆小球共有多少个
10-6x
10+6x
会应用
列方程解应用题.
两袋粮食共重160千克,第一袋用了 ,第二袋用了 共剩下80千克,那么原来第一袋粮食重多少千克
设谁为未知数呢?
设原来第一袋粮食重x千克
设原来第一袋粮食重x千克
设原来第二袋粮食重x千克
那么原来第二袋粮食重_______千克.
(160-x)
头脑风暴——找出等量关系列方程.
探索真相
解:设原来第一袋粮食重x千克.
解得x=_____.
100
答:原来第一袋粮食重100千克.
会应用
列方程解应用题.
小爱有55颗糖果,把这些糖果分成3份,第一份减3,第二份除以3,第三份乘3,所得的结果一致.你知道原来第三份糖果的颗数吗 (设出未知数,列方程即可,不解答)
设谁为未知数呢?
第一份
第二份
第三份
设所得的结果
设前面任意一个量,都不太好表示出另外2个量
第一份是_______颗.
(x+3)
设所得的结果为x
第二份是_______颗.
(x×3)
第三份是_______颗.
(x÷3)
会应用
列方程解应用题.
小爱有55颗糖果,把这些糖果分成3份,第一份减3,第二份除以3,第三份乘3,所得的结果一致.你知道原来第三份糖果的颗数吗 (设出未知数,列方程即可,不解答)
选择合适的量设未知数,找准等量关系.
总结
牛刀小试
过新年时,王老师给班里的学生分糖果,女生每人6块,男生每人5块,已知女生人数是男生的5分之4,且一共发了250块糖,你知道王老师班里有男生多少名吗
设男生有x名,那么女生有________名.
根据等量关系列方程_______________.
1
2
前情回顾
温故知新
容斥原理.
1
平均数问题.
2
音乐圈
舞蹈圈
只属于音乐圈
只属于舞蹈圈
既属于音乐圈
又属于舞蹈圈
平均数=总数量÷总份数
探索真相
会应用
六(1)班有30名学生,调查喜欢吃苹果和橘子的人数,发现每名学生至少喜欢其中的一种水果,调查结果是:有5分之4的学生喜欢吃苹果,有5分之3的学生喜欢吃橘子,两者都喜欢吃的学生人数占全班人数的几分之几?
法一
求出两者都喜欢吃的学生人数,再计算.
喜欢吃苹果的学生有____________(名)
喜欢吃橘子的学生有____________(名)
两者都喜欢吃的学生有___________(名)
两者都喜欢吃的学生人数占全班人数的__________.
18+24-30=12
12÷30=
探索真相
会应用
六(1)班有30名学生,调查喜欢吃苹果和橘子的人数,发现每名学生至少喜欢其中的一种水果,调查结果是:有5分之4的学生喜欢吃苹果,有5分之3的学生喜欢吃橘子,两者都喜欢吃的学生人数占全班人数的几分之几?
法二
直接计算.
两者都喜欢吃的学生人数占全班人数的_____________.
所有学生看作单位“1”
应
用
题
综
合
小升初数学
公 式
简单工程问题:
三要素:
工作总量、工作效率、工作时间
若工作总量没有告诉具体的数量,
我们可以设工作总量为单位“1"。
知识小结
例题讲解
合作的工作效率=
莎莎和莉莉决定将做好的小花串起来,莎莎单独完成需要5小时,莉莉单独完成需要8小时,则莎莎平均每小时可以完成全部工作的 ,莉莉平均每小时可以完成全部工作的 。莎莎和莉莉合作完成需要 小时。
修一条公路,甲单独完成需要4天,乙单独完成需要12天。如果两人合作,需要 天完成。
知识探索
将整个工程看作单位“1”
甲的工作效率:1÷4 =
乙的工作效率:1÷12=
甲、乙合作的工作效率:
甲、乙合作的工作时间:1÷ = 3(天)
例题讲解
一项工程,甲队单独完成需10天,乙队单独完成需15天,可是甲、乙两队的时间不能统一,所以他们决定轮流完成,如果甲队先做4天,乙队再接着做,则乙队需 天能将这个工程完成。
9
分 工 与 合 作
小提示:分干合想,合干分想
例题讲解
一项工程,甲队单独完成需40天,若乙队先做10天,余下的工程由甲、乙两队合作,再干20天即可完成。如果乙队单独完成此工程,则需 天。
等量关系式
工作总量 = 甲的工作量 + 乙的工作量
合作20天的工作量
合作20天的工作量
单干10天的工作量
60
知识探索
玩具加工厂需要加工一批玩具,师父单独加工12天可以完成。现在师父和徒弟一起加工了7天,然后让徒弟一个人接着干3天完成了这批玩具的加工。那么,这批玩具由徒弟单独做需要 天才能完成。
24
前情回顾
探索真相
三要素
单位“1”、分率、部分量
头脑风暴——找出三要素.
周一,松鼠妈妈带着小松鼠去采坚果,小松鼠采的坚果数是松鼠妈妈的 .
周三,松鼠妈妈又带着小松鼠去采坚果,这次松鼠妈妈采的坚果数是小松鼠的 .
部分量
单位1
分率
部分量
单位1
分率
探索真相
会应用
分数应用题(只列式不计算)
某小学六年级学生报名参加兴趣小组,已知参加数学小组的有32人.
英语小组的人数是数学小组的 ,英语小组有_______人.
语文小组的人数比数学小组多 ,语文小组有___________人。
数学小组的人数是美术小组的 ,美术小组有______人.
数学小组的人数比音乐小组多 ,音乐小组有___________人.
探索真相
会应用
小高家附近新开了一家老北京糖葫芦店。店主做了一些糖葫芦,由于开业大酬宾,很快就卖出了 ,于是店主又做了38根,此时的糖葫芦比原来的还多 ,你知道店主原来做了多少根糖葫芦吗
量率对应
“38根”对应的分率是______.
单位“1”未知,用除法
单位“1”=部分量÷分率
两个部分量对应的单位“1”一样吗?
A.一样 B. 不一样
探索真相
过难关
小帅的妈妈买了苹果、香蕉、梨三种水果,共4000克,他发现苹果的质量是香蕉和梨的 ,香蕉的质量是苹果和梨的 。那么梨的质量占三种水果总量的几分之几?
想一想如何计算?
小帅灵机一动,说应该是 .
你觉得正确吗?
观察分析
单位“1”不统一,
分率不能直接相加减。
探索真相
过难关
单位“1”不统一,先统一单位“1”。
分析
将单位“1”统一为谁呢?
三种水果的总量。
苹果的质量是其余两种水果的 .
3份
5份
苹果的质量占总量的
香蕉的质量是其余两种水果的 .
香蕉的质量占总量的
梨的质量占三种水果总量的_______________.
2份
5份
3份
通过部分与整体统一单位“1”:遇到多个分率的单位“1”不统一时,先统一单位“1”.
总结
比的应用——利用不变量解决相关问题
甲、乙两个盒子中分别装有一些小球,它们的数量比是3:5.
分析下面每种情况,找准不变量,再连线。
连一连
会应用
比的应用——部分量不变
甲、乙两个盒子中分别装有一些小球,它们的数量比是3:5.再往甲盒中放入9个小球,数量比变为3:4. 原来甲、乙两个盒子中分别有多少个小球
思考:谁是不变量?
乙盒中的小球的数量是不变量.
甲 乙 统一后
原来 3 5 12 20
现在 3 4 15 20
=
=
:
:
:
:
1份:_____________(个);
原甲盒:__________(个);
原乙盒:__________(个).
9÷(15-12)=3
3x12=36
3x20=60
统一不变量的份数,关键是求1份量 ,再按比分配.
会应用
比的应用——和不变
甲、乙两个盒子中分别装有一些小球,它们的数量比是3:5. 从乙盒中拿出8个小球放入甲盒,数量比变为1:1,找到不变量统一份数.
思考:谁是不变量?
甲、乙两盒中小球的数量和是不变量.
对比分析
甲 乙 和
原来 3 5 8
现在 1 1 2
统一后 ×4 ×4 2×4=8
牛刀小试
练习
小爱养了红色、黄色、黑色三种颜色的小鱼,其中红色小鱼是其他两种小鱼总数的 ,黄色小鱼是其他两种小鱼总数的 .
红色小鱼是三种小鱼总数的________;
1
黄色小鱼是三种小鱼总数的________.
2
前情回顾
注意
设未知数的方法:
①直接设;②设单位“1”或1倍量;
③设容易表示其他量的为x.
列:根据等量关系列方程
探索真相
用字母表示数.
一站到底
A、B两袋面粉共400千克,吃了A袋面粉的40%.
设B袋面粉为x千克,那么吃了A袋面粉多少千克
40% ×(400-x)
400-40%x
探索真相
用字母表示数.
一站到底
某校六年级男生与女生人数相同,六年级女老师人数是男老师的2倍,且女老师与男生共128人.设六年级男老师有x人,那么女生有多少人
128-2x
128+2x
探索真相
用字母表示数.
一站到底
有一堆小球,每次取出6个,取了x次后,还剩10个小球那么原来这堆小球共有多少个
10-6x
10+6x
会应用
列方程解应用题.
两袋粮食共重160千克,第一袋用了 ,第二袋用了 共剩下80千克,那么原来第一袋粮食重多少千克
设谁为未知数呢?
设原来第一袋粮食重x千克
设原来第一袋粮食重x千克
设原来第二袋粮食重x千克
那么原来第二袋粮食重_______千克.
(160-x)
头脑风暴——找出等量关系列方程.
探索真相
解:设原来第一袋粮食重x千克.
解得x=_____.
100
答:原来第一袋粮食重100千克.
会应用
列方程解应用题.
小爱有55颗糖果,把这些糖果分成3份,第一份减3,第二份除以3,第三份乘3,所得的结果一致.你知道原来第三份糖果的颗数吗 (设出未知数,列方程即可,不解答)
设谁为未知数呢?
第一份
第二份
第三份
设所得的结果
设前面任意一个量,都不太好表示出另外2个量
第一份是_______颗.
(x+3)
设所得的结果为x
第二份是_______颗.
(x×3)
第三份是_______颗.
(x÷3)
会应用
列方程解应用题.
小爱有55颗糖果,把这些糖果分成3份,第一份减3,第二份除以3,第三份乘3,所得的结果一致.你知道原来第三份糖果的颗数吗 (设出未知数,列方程即可,不解答)
选择合适的量设未知数,找准等量关系.
总结
牛刀小试
过新年时,王老师给班里的学生分糖果,女生每人6块,男生每人5块,已知女生人数是男生的5分之4,且一共发了250块糖,你知道王老师班里有男生多少名吗
设男生有x名,那么女生有________名.
根据等量关系列方程_______________.
1
2
前情回顾
温故知新
容斥原理.
1
平均数问题.
2
音乐圈
舞蹈圈
只属于音乐圈
只属于舞蹈圈
既属于音乐圈
又属于舞蹈圈
平均数=总数量÷总份数
探索真相
会应用
六(1)班有30名学生,调查喜欢吃苹果和橘子的人数,发现每名学生至少喜欢其中的一种水果,调查结果是:有5分之4的学生喜欢吃苹果,有5分之3的学生喜欢吃橘子,两者都喜欢吃的学生人数占全班人数的几分之几?
法一
求出两者都喜欢吃的学生人数,再计算.
喜欢吃苹果的学生有____________(名)
喜欢吃橘子的学生有____________(名)
两者都喜欢吃的学生有___________(名)
两者都喜欢吃的学生人数占全班人数的__________.
18+24-30=12
12÷30=
探索真相
会应用
六(1)班有30名学生,调查喜欢吃苹果和橘子的人数,发现每名学生至少喜欢其中的一种水果,调查结果是:有5分之4的学生喜欢吃苹果,有5分之3的学生喜欢吃橘子,两者都喜欢吃的学生人数占全班人数的几分之几?
法二
直接计算.
两者都喜欢吃的学生人数占全班人数的_____________.
所有学生看作单位“1”
同课章节目录
