苏教版2025年三年级下学期数学(期末巩固)暑假伴学营分类专训系列:应用题培优训练(含解析)
文档属性
| 名称 | 苏教版2025年三年级下学期数学(期末巩固)暑假伴学营分类专训系列:应用题培优训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 416.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 14:31:27 | ||
图片预览




文档简介
苏教版2025年三年级下学期数学(期末巩固)暑假伴学营分类专训系列:应用题培优训练
学校:___________姓名:___________班级:___________
解答题
1.哥哥拿出自己零花钱的给弟弟,弟弟用这些钱的给妈妈买了一束鲜花,还剩14元。哥哥原来有多少零花钱?
2.刘阿姨家有一块正方形菜地(如图),在扩建时把一组对边各增加8米,形成长方形后,面积增加了240平方米。原来正方形的面积是多少平方米?(先把条件和问题在示意图上表示出来,再解答)
3.2024年3月22日是第三十二届“世界水日”,3月22日-28日是第三十七届“中国水周”。水是生命之源,我们要节约每一滴水。小明家去年第二季度缴纳水费114元,第三季度每月缴纳水费32元。
(1)第二季度和第三季度一共缴纳水费多少元?
(2)第二季度比第三季度平均每月多缴纳水费多少元?
(3)如果每人每天节约2千克水,小明一家3人今年上半年一共可以节约水多少千克?
4.如图,一个长方形和一个正方形部分重合,两块没有重合的部分(涂色部分)面积相差多少平方厘米?
5.王老师给小朋友分饼干,如果每人分5块,少了15块;如果每人分3块,多了31块。小朋友有多少个?饼干有多少块?
6.你认为够不够呢?在下面写一写、画一画。
7.张叔叔用32米长的篱笆围成一个长方形或正方形的苗圃(没有剩余,长、宽为整米数),怎样围这个苗圃的面积最大?是多少平方米?怎样围这个苗圃的面积最小?是多少平方米?
8.已知大正方形的边长比小正方形的边长多2厘米,大正方形的面积比小正方形的面积大40平方厘米。大、小正方形的面积各是多少平方厘米?
9.有6个箱子,每个箱子中装着同样多的桃子,如果从每箱中取走16个桃子,那么6个箱子中剩下的桃子总数等于原来2箱的桃子数。原来每箱桃子有多少个?
10.在学校的文艺演出中,小演员们在舞台的中央排成了一个空心正方形,每条边上站了16人(四个顶点都站有1人)。这个舞台上共有多少位小演员?
11.商场的自动扶梯以均匀的速度由下往上行驶着,兄妹两人乘自动扶梯上楼,哥哥每分钟走20级,妹妹每分钟走15级,结果哥哥5分钟到达楼上,妹妹6分钟到达楼上,问该自动扶梯有多少级可见扶梯?
12.有一张长方形(不包含正方形)的周长是200厘米,且长和宽都是整数。问:当长和宽是多少时它的面积最大?当长和宽是多少时,它的面积最小?
13.王亮要从一张长10厘米、宽8厘米的纸上剪下一个最大的正方形,剩下的部分是一个什么图形?它的面积是多少平方厘米?周长呢?
14.清明节,盛明明一家去“安徒生乐园”游玩,景区内的停车场2小时内收费5元,如果超过2小时每多停1小时要多付3元(不足1小时按照1小时算)亮亮的爸爸离开停车场时付了29元,他最多停车几小时?
15.张爷爷家的菜园有一块长方形空地,如果长增加6米,或宽增加4米,面积都比原来增加48平方米。原来长方形空地的面积是多少平方米?
16.小马虎在读一个数时,把小数点丢了,结果读成了三千零九。原来的小数读出来要读两个零,你能帮小马虎正确地读出这个数吗?
17.用长36米的竹篱笆围成一个长方形菜园,围成菜园的最大面积是多少?
18.哪些动物可以一起过桥?(桥限重1吨)
19.下面是某铁路沿线A站到E站的火车里程表.
到站情况 里程/千米
A站﹣B站 164
A站﹣C站 322
A站﹣D站 448
A站﹣E站 1142
(1)根据上图完成下表
到站情况 里程/千米
B站﹣C站
C站﹣D站
D站﹣E站
(2)从B站到E站一个来回多少千米?
(3)从C站到E站和B站到D站哪段路程长?长多少千米?
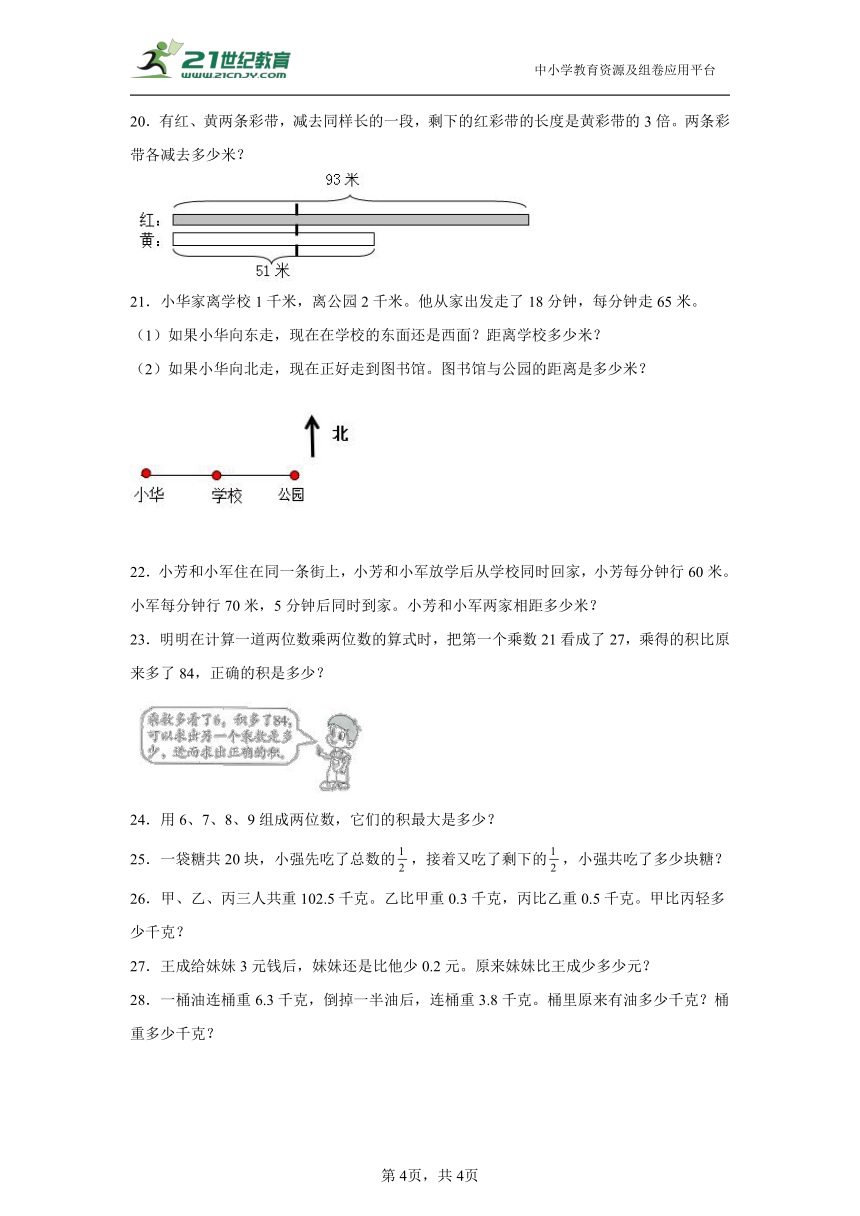
20.有红、黄两条彩带,减去同样长的一段,剩下的红彩带的长度是黄彩带的3倍。两条彩带各减去多少米?
21.小华家离学校1千米,离公园2千米。他从家出发走了18分钟,每分钟走65米。
(1)如果小华向东走,现在在学校的东面还是西面?距离学校多少米?
(2)如果小华向北走,现在正好走到图书馆。图书馆与公园的距离是多少米?
22.小芳和小军住在同一条街上,小芳和小军放学后从学校同时回家,小芳每分钟行60米。小军每分钟行70米,5分钟后同时到家。小芳和小军两家相距多少米?
23.明明在计算一道两位数乘两位数的算式时,把第一个乘数21看成了27,乘得的积比原来多了84,正确的积是多少?
24.用6、7、8、9组成两位数,它们的积最大是多少?
25.一袋糖共20块,小强先吃了总数的,接着又吃了剩下的,小强共吃了多少块糖?
26.甲、乙、丙三人共重102.5千克。乙比甲重0.3千克,丙比乙重0.5千克。甲比丙轻多少千克?
27.王成给妹妹3元钱后,妹妹还是比他少0.2元。原来妹妹比王成少多少元?
28.一桶油连桶重6.3千克,倒掉一半油后,连桶重3.8千克。桶里原来有油多少千克?桶重多少千克?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第2页,共4页
第3页,共4页
参考答案
1.245元
【分析】哥哥拿出自己的零花钱的给弟弟,则把哥哥零花钱总数看成一个整体,平均分成7份,拿出2份给弟弟,弟弟用了这些钱的,即把这些钱平均分成5份,弟弟用了其中4份,1-=,还剩下1份,是14元,则弟弟的总钱数为14×5=70(元),70元钱占哥哥零花钱总数的,用70除以2,计算出每份是多少,再乘7,即可算出哥哥有多少零花钱。据此解答。
【详解】1-=
14×5=70(元)
70÷2×7
=35×7
=245(元)
答:哥哥原来有245元零花钱。
【点睛】本题主要考查分数的简单运用,此题知道一个数的几分之几是多少,要求这个数,解答时要注意找准每个数字对应着分数中的哪一部分。
2.见详解;900平方米
【分析】根据题意,在扩建时把一组对边各增加8米,形成长方形后,面积增加了240平方米,利用长方形面积公式:S=ab计算原来正方形的边长;再利用正方形面积公式:S=a 计算正方形的面积即可。
【详解】如图所示:
240÷8=30(米)
30×30=900(平方米)
答:原来正方形的面积是900平方米。
【点睛】本题主要考查长方形面积公式的应用,需熟记公式。
3.(1)210元;
(2)6元;
(3)1092千克
【分析】(1)第三季度每月缴纳水费32元,每季度有3个月,用32×3,即可得到第三季度缴纳的水费,将第二季度和第三季度缴纳的水费相加,即可得到第二季度和第三季度一共缴纳水费多少元;
(2)第二季度缴纳水费114元,每季度有3个月,用114÷3,即可得到第二季度每月缴纳水费多少元,用第二季度每月缴纳的水费减去第三季度每月缴纳的水费,即可得到第二季度比第三季度平均每月多缴纳水费多少元;
(3)上半年一共包括1月、2月、3月、4月、5月、6月,今年是2024年,用2024÷4,若没有余数,即今年为闰年,2月有29天,否则今年为平年,2月只有28天;1月、3月、5月这个3月,每个月有31天,4月和6月每个月有30天,因此可将这六个月的天数相加,得到2024年上半年的天数。小明一家3人,每人每天节约2千克水,用上半年的天数乘人数,再乘每人每天节约水的量,即可求得小明一家3人今年上半年一共可以节约水多少千克。
【详解】(1)32×3=96(元)
114+96=210(元)
答:第二季度和第三季度一共缴纳水费210元。
(2)114÷3=38(元)
38-32=6(元)
答:第二季度比第三季度平均每月多缴纳水费6元。
(3)2024÷4=506
因此2024年为闰年,2月有29天
31×3+30×2+29=93+60+29=153+29=182(天)
182×3×2=546×2=1092(千克)
答:小明一家3人今年上半年一共可以节约水1092千克。
【点睛】此题考查了闰年和平年的判定方法,在解题的过程中需要知道一个季度为三个月,并且计算较为复杂,需要更加仔细。
4.24平方厘米
【分析】分析题意观察图可知:左面涂色部分面积=长方形的面积-重合部分面积,右面涂色部分面积=正方形的面积-重合部分面积。根据差的变化规律(被减数和减数同时减去一个相同的数,差不变),两块没有重合的部分的面积差就是长方形和正方形的面积差。
【详解】8×5=40(平方厘米)
4×4=16(平方厘米)
40-16=24(平方厘米)
答:两块没有重合的部分(涂色部分)面积相差24平方厘米。
【点睛】掌握差的变化规律是解题的关键。
5.23个;100块
【分析】按照第一种分法每人分5块,少了15块,第二种分法每人分3块,多了31块,两次分配一共相差15+31=46(块),相差46块是由于每人相差5-3=2(块),那么46中有多少个2,就是有多少小朋友参加分配。人数×5-15块=饼干的块数,依此解答。
【详解】(15+31)÷(5-3)
=46÷2
=23(个)
23×5-15
=115-15
=100(块)
答:小朋友有23个,饼干有100块。
【点睛】盈亏问题的解答思路是:通过比较已知条件,找出两个相关的差数,一是总差额,二是每份的差额,将这两个差相除,就可求出总份数,基本关系式为:总差额÷每份的差额=总人数。
6.不够(理由见解析)
【分析】如下图,假设这串葡萄有12颗,葡萄的颗数除以分母再乘分子分别求出两个小动物要拿的颗数,然后相加,如果超过这串葡萄的总颗数就不够,否则就够,据此即可解答。
【详解】假设这串葡萄有12颗。
12÷2×1
=6×1
=6(颗)
12÷6×5
=2×5
=10(颗)
6颗+10颗>12颗,所以不够分。
答:不够分。
【点睛】本题可以先设这串葡萄有多少颗,然后利用除法求一个数的几分之几是多少求出两小动物要拿的颗数,再作进一步解答。
7.边长8米的正方形面积最大,是64平方米;长15米,宽1米的长方形面积最小,是15平方米
【分析】根据长方形的周长=(长+宽)×2,正方形的周长=边长×4,篱笆长32米,围成长方形的长宽和是16米,围成正方形的边长是8米。当长方形长宽差最小时,苗圃面积最大,也就是围成正方形时苗圃面积最大。当长方形的长宽差最大时,苗圃面积最小,此时长方形长15米,宽1米。根据长方形的面积=长×宽,正方形的面积=边长×边长解答。
【详解】32÷4=8(米)
8×8=64(平方米)
(15+1)×2
=16×2
=32(米)
15×1=15(平方米)
答:围成边长为8米的正方形时,面积最大,是64平方米。围成长15米宽1米的长方形时,面积最小,是15平方米。
【点睛】长方形的周长固定,长宽差越大,面积越小,长宽差越小,面积越大,若能围成正方形,正方形的面积最大。
8.大正方形的面积是121平方厘米,小正方形的面积是81平方厘米
【分析】根据题意画图如下:大正方形比小正方形的面积大的部分由3部分组成(黄色和黑色),其中2个黄色部分一样大,且黄色长方形的长为小正方形的边长,宽为2厘米,黑色部分是一个边长为2厘米的小正方形,面积是(2×2)平方厘米。所以小正方形的边长:(40-2×2)÷2÷2厘米,根据正方形的面积=边长×边长,求出小正方形的面积。再用小正方形的面积加上40平方厘米,求出大正方形的面积。
【详解】(40-2×2)÷2÷2
=(40-4)÷2÷2
=36÷2÷2
=18÷2
=9(厘米)
9×9=81(平方厘米)
81+40=121(平方厘米)
答:大正方形的面积是121平方厘米,小正方形的面积是81平方厘米。
【点睛】本题考查正方形面积公式的应用,关键是根据题意,画出图,帮助我们分析题中面积之间的关系。
9.24个
【分析】剩下的桃子总数等于原来2箱的桃子数,那么取走的桃子数就等于原来4箱的桃子数。用16乘6求出4箱桃子的总个数,再除以4即可求出原来每箱桃子的个数。
【详解】6-2=4(个)
16×6=96(个)
96÷4=24(个)
答:原来每箱桃子有24个。
【点睛】解答此题的关键是明确取走的桃子数就等于原来4箱的桃子数。
10.60位
【分析】用16乘4的积再减去4即可求出这个舞台上共有多少位小演员,据此解答。
【详解】16×4-4
=64-4
=60(位)
答:这个舞台上共有60位小演员。
【点睛】本题考查了正方形的周长公式,学生应熟练掌握并灵活运用。
11.150级
【分析】根据“哥哥每分钟走20级,结果哥哥5分钟到达楼上,”可以求出哥哥走的扶梯的个数,列式为:20×5=100级;根据“妹每分钟走15级,妹6分钟到达楼上”可以求出妹妹走的扶梯的个数,列式为:15×6=90级;再根据哥哥和妹妹走的扶梯的个数,可以求出自动扶梯的速度为:(100-90)÷(6-5)=10级;由于人和扶梯是同向运动的所以自动扶梯可见部分的个数为:(20+10)×5=150级,问题得解。
【详解】自动扶梯的速度为:
(20×5-15×6)÷(6-5)
=(100-90)÷1
=10(级)
自动扶梯可见部分的个数为:
(20+10)×5
=30×5
=150(级)
答:该自动扶梯有150级可见扶梯。
【点睛】此题考查的是和差问题,要理解上楼的速度可以分为两部分:一部分是兄妹的自己的速度,另一部分是自动扶梯的速度,所以利用和差知识求出自动扶梯的速度是本题的关键。
12.51厘米和49厘米;99厘米和1厘米
【分析】长方形的周长一定的情况下,长与宽越接近,它的面积越大,反之它的面积就越小,据此解答。
【详解】200÷2=100(厘米)
100=51+49,当长和宽分别是51厘米和49厘米时,面积最大。
100=1+99,当长和宽分别是99厘米和1厘米时,面积最小。
答:当长和宽分别是51厘米和49厘米时,面积最大。当长和宽分别是99厘米和1厘米时,面积最小。
【点睛】此题主要考查了长方形周长一定时,长和宽的长度与长方形面积之间的关系;长与宽的差越小它的面积就越大。
13.长方形;16平方厘米;20厘米
【分析】根据题意可知,要从一个长10厘米、宽8厘米的长方形上剪下一个最大的正方形,这个正方形的边长等于长方形的宽,即8厘米;剩下的部分是一个长8厘米、宽(10-8)厘米的长方形;再根据长方形面积=长×宽、长方形周长=(长+宽)×2,即可求剩下部分的面积和周长。
【详解】根据题意可知,剪下的正方形的边长是8厘米,剩下部分是一个长8厘米、宽(10-8)厘米的长方形。
8×(10-8)
=8×2
=16(平方厘米)
[8+(10-8)]×2
=[8+2]×2
=10×2
=20(厘米)
答:剩下部分是一个长8厘米、宽2厘米的长方形,它的面积是16平方厘米,周长是20厘米。
【点睛】确定剪下的正方形的边长是解答此题的关键。
14.10小时
【分析】根据题意可得,29元超过了5元,说明停车时间超过了2小时;先算出超过2小时的部分所花的钱数,再除以3元,即可求出超过2小时的部分是多少小时,再加上2小时就是总时间,据此解答即可。
【详解】(29-5)÷3+2
=24÷3+2
=8+2
=10(小时)
答:他最多停车10小时。
【点睛】此题考查了整数的四则混合运算,关键是求出超过2小时的费用和时间即可。
15.96平方米
【分析】长方形的面积=长×宽,先假设增加的是长,然后根据增加的面积求出原来长方形的宽,再根据增加的宽,求出原来长方形的长,最后再求出原来长方形空地的面积即可。
【详解】48÷6=8(米)
48÷4=12(米)
12×8=96(平方米)
答:原来长方形空地的面积是96平方米。
【点睛】熟练掌握长方形面积的实际运用是解答此题的关键。
16.三点零零九
【分析】先把小马虎读错的数写出来,再根据小数的读法进一步推出原来的小数即可。
【详解】三千零九写作:3009,原来的小数读出来要读两个零,所以正确的小数是3.009,故读作三点零零九。
答:正确的读法是三点零零九。
【点睛】熟练掌握小数的读写知识是解答本题的关键。
17.80平方米
【分析】根据长方形的周长公式:C=(a+b)÷2,那么a+b=C÷2,据此求出长与宽的和,当长与宽的差越小时,长方形的面积就越多,由此可以求出长与宽,然后根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】36÷2=18(米)
18=17+1=16+2=15+3=14+4=13+5=12+6=11+7=10+8
10×8=80(平方米)
答:围成菜园的面积最大是80平方米。
【点睛】此题主要考查长方形的周长公式、面积公式的灵活运用,关键是熟记公式。
18.熊、猪和鹿可以一起过桥,牛、猪和鹿可以一起过桥。
【分析】根据题意可知,这座桥限重1吨,也就是1000千克,在这4种动物中,看哪几种动物合起来等于或小于1吨,就可以一起过桥,据此解答。
【详解】1吨=1000千克,
480+190+150=820(千克)
600+190+150=940(千克)
答:熊、猪和鹿可以一起过桥,牛、猪和鹿可以一起过桥。
【点睛】此题考查的目的是理解掌握质量单位吨与千克之间的进率及换算,以及整数加法的计算法则、整数大小比较的方法及应用。
19.(1)
到站情况 里程/千米
B站﹣C站 158
C站﹣D站 126
D站﹣E站 694
(2)1956千米
(3)从C站到E站的路程长,长536千米
【分析】(1)B站到C站的里程=A站到C站的里程-A站到B站的里程;C站到D站的里程=A站到D站的里程- A站到C站的里程;D站到E站的里程=A站到E站的里程-A站到D站的里程,据此代入数据作答即可.
(2)从B站到E站一个来回的距离=(A站到E站的里程- A站到B站的里程)×2,据此代入数据作答即可;
(3)C站到E站的里程=A站到E站的里程-A站到C站的里程,B站到D站的里程=A站到D站的里程-A站到B站的里程,哪个数大说明哪段路长,长出的千米数=远的那段路程的长度-短的那段路程的长度,据此代入数据作答即可.
【详解】(1)B站﹣C站:322﹣164=158(千米),
C站﹣D站:448﹣322=126(千米),
D站﹣E站:1142﹣448=694(千米),
(2)(1142﹣164)×2
=978×2
=1956(千米)
答:从B站到E站一个来回有1956千米.
(3)C站﹣E站:1142﹣322=820(千米)
B站﹣D站:448﹣164=284(千米)
820﹣284=536(千米)
答:从C站到E站的路程长,长536千米.
20.30米
【分析】因为它们减去相同的1段,差是不变的,一直是93-51=42(米),红彩带是黄彩带的3倍,所以黄彩带剩下的部分就是42÷(3-1)=21米,减去的部分就用黄彩带总的长度减去剩下的部分就可以得出答案。
【详解】根据分析:
93-51=42(米)
42÷(3-1)
=42÷2
=21(米)
51-21=30(米)
答:两条彩带各减去30米。
【点睛】本题主要考查的是整数的复合应用题,对于这类问题就要根据相互关联的数量关系找出已知数量和未知数量的联系,先解答一个或几个中间问题,也就是把它先分解成几个简单应用题,然后再根据它们的联系依次列式并求解。
21.(1)东面;170米
(2)3170米
【分析】算出每分钟走65米,18分钟走的路程为65×18=1170米;
(1)小华家离学校1千米,向东走1170米,超过到学校的距离,就到了学校的东面;
(2)小华家离公园2千米,向北走1170米,将小华家与图书馆的距离和小华家到公园的距离加起来即可。
【详解】(1)65×18=1170(米)
1千米=1000米
1000<1170
超过了学校,现在在学校东面
1170-1000=170(米)
答:现在在学校东面,距离学校170米。
(2)2千米=2000米
1170+2000=3170(米)
答:图书馆与公园的距离是3170米。
【点睛】此题考查行程问题和方向的辨别,注意结合图形,根据数据和方向确定位置。
22.650米或50米
【分析】如果他们两人在学校的两侧,用加法解答,小芳每分钟行60米,5分钟到家,小芳家离学校的距离为60×5,同理,小军家离学校的距离是70×5,要求小芳家到小军家的距离,把这两部分加起来即可;如果他们两家在学校的同一侧,根据减法的意义,用减法解答。
【详解】60×5+70×5
=300+350
=650(米)
70×5-60×5
=350-300
=50(米)
答:小芳和小军两家相距650米或50米。
【点睛】此题解答关键是明确:他们两家在学校的同一侧,还是在学校的两侧。
23.294
【分析】27比21多6,乘积多了84,说明乘积多了第一个因数的6倍,这样用84除以6即可求出第一个因数,然后用乘法计算出正确的积即可。
【详解】27-21=6
84÷6=14
21×14=294
答:正确的积是294。
24.8352
【分析】根据整数乘法计算法则,必须先使十位数最大,且使较小的十位数字后面的个位数较大,才能使它和较大的两位数相乘,确保乘积最大。
【详解】96×87=8352
答:它们的积最大应是8352。
【点睛】关键明白,要使这两个数的积最大,首先必须这两个数最大。
25.15块
【详解】20÷2+(20-20÷2)÷2=15(块)
26.0.8千克
【分析】根据题意,乙比甲重0.3千克,也就是说甲比乙少了0.3千克,丙比乙又多0.5千克,这样甲就比丙少了0.3+0.5千克,由此解答。
【详解】0.3+0.5=0.8(千克)
答:甲比丙轻0.8千克。
【点睛】解答本题的关键是找到乙作为甲和丙的中间参考量,用他们与乙的轻重关系来得出答案。
27.6.2元
【分析】王成给妹妹3元钱后,王成的钱减少了3元,这样两人的差就缩小了(3+3)元,再加上现在的相差的钱数,就是原来两人相差的钱数,由此求解。
【详解】3+3+0.2
=6+0.2
=6.2(元)
答:原来妹妹比王成少6.2元。
【点睛】解决本题关键是理解两人的钱数差减少了2个3元,而不是1个3元,然后再进一步求解。
28.5千克;1.3千克
【详解】3.8+3.8=7.6(千克)
桶重:7.6-6.3=1.3(千克)
油重:6.3-1.3=5(千克)
第12页,共12页
第11页,共12页
学校:___________姓名:___________班级:___________
解答题
1.哥哥拿出自己零花钱的给弟弟,弟弟用这些钱的给妈妈买了一束鲜花,还剩14元。哥哥原来有多少零花钱?
2.刘阿姨家有一块正方形菜地(如图),在扩建时把一组对边各增加8米,形成长方形后,面积增加了240平方米。原来正方形的面积是多少平方米?(先把条件和问题在示意图上表示出来,再解答)
3.2024年3月22日是第三十二届“世界水日”,3月22日-28日是第三十七届“中国水周”。水是生命之源,我们要节约每一滴水。小明家去年第二季度缴纳水费114元,第三季度每月缴纳水费32元。
(1)第二季度和第三季度一共缴纳水费多少元?
(2)第二季度比第三季度平均每月多缴纳水费多少元?
(3)如果每人每天节约2千克水,小明一家3人今年上半年一共可以节约水多少千克?
4.如图,一个长方形和一个正方形部分重合,两块没有重合的部分(涂色部分)面积相差多少平方厘米?
5.王老师给小朋友分饼干,如果每人分5块,少了15块;如果每人分3块,多了31块。小朋友有多少个?饼干有多少块?
6.你认为够不够呢?在下面写一写、画一画。
7.张叔叔用32米长的篱笆围成一个长方形或正方形的苗圃(没有剩余,长、宽为整米数),怎样围这个苗圃的面积最大?是多少平方米?怎样围这个苗圃的面积最小?是多少平方米?
8.已知大正方形的边长比小正方形的边长多2厘米,大正方形的面积比小正方形的面积大40平方厘米。大、小正方形的面积各是多少平方厘米?
9.有6个箱子,每个箱子中装着同样多的桃子,如果从每箱中取走16个桃子,那么6个箱子中剩下的桃子总数等于原来2箱的桃子数。原来每箱桃子有多少个?
10.在学校的文艺演出中,小演员们在舞台的中央排成了一个空心正方形,每条边上站了16人(四个顶点都站有1人)。这个舞台上共有多少位小演员?
11.商场的自动扶梯以均匀的速度由下往上行驶着,兄妹两人乘自动扶梯上楼,哥哥每分钟走20级,妹妹每分钟走15级,结果哥哥5分钟到达楼上,妹妹6分钟到达楼上,问该自动扶梯有多少级可见扶梯?
12.有一张长方形(不包含正方形)的周长是200厘米,且长和宽都是整数。问:当长和宽是多少时它的面积最大?当长和宽是多少时,它的面积最小?
13.王亮要从一张长10厘米、宽8厘米的纸上剪下一个最大的正方形,剩下的部分是一个什么图形?它的面积是多少平方厘米?周长呢?
14.清明节,盛明明一家去“安徒生乐园”游玩,景区内的停车场2小时内收费5元,如果超过2小时每多停1小时要多付3元(不足1小时按照1小时算)亮亮的爸爸离开停车场时付了29元,他最多停车几小时?
15.张爷爷家的菜园有一块长方形空地,如果长增加6米,或宽增加4米,面积都比原来增加48平方米。原来长方形空地的面积是多少平方米?
16.小马虎在读一个数时,把小数点丢了,结果读成了三千零九。原来的小数读出来要读两个零,你能帮小马虎正确地读出这个数吗?
17.用长36米的竹篱笆围成一个长方形菜园,围成菜园的最大面积是多少?
18.哪些动物可以一起过桥?(桥限重1吨)
19.下面是某铁路沿线A站到E站的火车里程表.
到站情况 里程/千米
A站﹣B站 164
A站﹣C站 322
A站﹣D站 448
A站﹣E站 1142
(1)根据上图完成下表
到站情况 里程/千米
B站﹣C站
C站﹣D站
D站﹣E站
(2)从B站到E站一个来回多少千米?
(3)从C站到E站和B站到D站哪段路程长?长多少千米?
20.有红、黄两条彩带,减去同样长的一段,剩下的红彩带的长度是黄彩带的3倍。两条彩带各减去多少米?
21.小华家离学校1千米,离公园2千米。他从家出发走了18分钟,每分钟走65米。
(1)如果小华向东走,现在在学校的东面还是西面?距离学校多少米?
(2)如果小华向北走,现在正好走到图书馆。图书馆与公园的距离是多少米?
22.小芳和小军住在同一条街上,小芳和小军放学后从学校同时回家,小芳每分钟行60米。小军每分钟行70米,5分钟后同时到家。小芳和小军两家相距多少米?
23.明明在计算一道两位数乘两位数的算式时,把第一个乘数21看成了27,乘得的积比原来多了84,正确的积是多少?
24.用6、7、8、9组成两位数,它们的积最大是多少?
25.一袋糖共20块,小强先吃了总数的,接着又吃了剩下的,小强共吃了多少块糖?
26.甲、乙、丙三人共重102.5千克。乙比甲重0.3千克,丙比乙重0.5千克。甲比丙轻多少千克?
27.王成给妹妹3元钱后,妹妹还是比他少0.2元。原来妹妹比王成少多少元?
28.一桶油连桶重6.3千克,倒掉一半油后,连桶重3.8千克。桶里原来有油多少千克?桶重多少千克?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第2页,共4页
第3页,共4页
参考答案
1.245元
【分析】哥哥拿出自己的零花钱的给弟弟,则把哥哥零花钱总数看成一个整体,平均分成7份,拿出2份给弟弟,弟弟用了这些钱的,即把这些钱平均分成5份,弟弟用了其中4份,1-=,还剩下1份,是14元,则弟弟的总钱数为14×5=70(元),70元钱占哥哥零花钱总数的,用70除以2,计算出每份是多少,再乘7,即可算出哥哥有多少零花钱。据此解答。
【详解】1-=
14×5=70(元)
70÷2×7
=35×7
=245(元)
答:哥哥原来有245元零花钱。
【点睛】本题主要考查分数的简单运用,此题知道一个数的几分之几是多少,要求这个数,解答时要注意找准每个数字对应着分数中的哪一部分。
2.见详解;900平方米
【分析】根据题意,在扩建时把一组对边各增加8米,形成长方形后,面积增加了240平方米,利用长方形面积公式:S=ab计算原来正方形的边长;再利用正方形面积公式:S=a 计算正方形的面积即可。
【详解】如图所示:
240÷8=30(米)
30×30=900(平方米)
答:原来正方形的面积是900平方米。
【点睛】本题主要考查长方形面积公式的应用,需熟记公式。
3.(1)210元;
(2)6元;
(3)1092千克
【分析】(1)第三季度每月缴纳水费32元,每季度有3个月,用32×3,即可得到第三季度缴纳的水费,将第二季度和第三季度缴纳的水费相加,即可得到第二季度和第三季度一共缴纳水费多少元;
(2)第二季度缴纳水费114元,每季度有3个月,用114÷3,即可得到第二季度每月缴纳水费多少元,用第二季度每月缴纳的水费减去第三季度每月缴纳的水费,即可得到第二季度比第三季度平均每月多缴纳水费多少元;
(3)上半年一共包括1月、2月、3月、4月、5月、6月,今年是2024年,用2024÷4,若没有余数,即今年为闰年,2月有29天,否则今年为平年,2月只有28天;1月、3月、5月这个3月,每个月有31天,4月和6月每个月有30天,因此可将这六个月的天数相加,得到2024年上半年的天数。小明一家3人,每人每天节约2千克水,用上半年的天数乘人数,再乘每人每天节约水的量,即可求得小明一家3人今年上半年一共可以节约水多少千克。
【详解】(1)32×3=96(元)
114+96=210(元)
答:第二季度和第三季度一共缴纳水费210元。
(2)114÷3=38(元)
38-32=6(元)
答:第二季度比第三季度平均每月多缴纳水费6元。
(3)2024÷4=506
因此2024年为闰年,2月有29天
31×3+30×2+29=93+60+29=153+29=182(天)
182×3×2=546×2=1092(千克)
答:小明一家3人今年上半年一共可以节约水1092千克。
【点睛】此题考查了闰年和平年的判定方法,在解题的过程中需要知道一个季度为三个月,并且计算较为复杂,需要更加仔细。
4.24平方厘米
【分析】分析题意观察图可知:左面涂色部分面积=长方形的面积-重合部分面积,右面涂色部分面积=正方形的面积-重合部分面积。根据差的变化规律(被减数和减数同时减去一个相同的数,差不变),两块没有重合的部分的面积差就是长方形和正方形的面积差。
【详解】8×5=40(平方厘米)
4×4=16(平方厘米)
40-16=24(平方厘米)
答:两块没有重合的部分(涂色部分)面积相差24平方厘米。
【点睛】掌握差的变化规律是解题的关键。
5.23个;100块
【分析】按照第一种分法每人分5块,少了15块,第二种分法每人分3块,多了31块,两次分配一共相差15+31=46(块),相差46块是由于每人相差5-3=2(块),那么46中有多少个2,就是有多少小朋友参加分配。人数×5-15块=饼干的块数,依此解答。
【详解】(15+31)÷(5-3)
=46÷2
=23(个)
23×5-15
=115-15
=100(块)
答:小朋友有23个,饼干有100块。
【点睛】盈亏问题的解答思路是:通过比较已知条件,找出两个相关的差数,一是总差额,二是每份的差额,将这两个差相除,就可求出总份数,基本关系式为:总差额÷每份的差额=总人数。
6.不够(理由见解析)
【分析】如下图,假设这串葡萄有12颗,葡萄的颗数除以分母再乘分子分别求出两个小动物要拿的颗数,然后相加,如果超过这串葡萄的总颗数就不够,否则就够,据此即可解答。
【详解】假设这串葡萄有12颗。
12÷2×1
=6×1
=6(颗)
12÷6×5
=2×5
=10(颗)
6颗+10颗>12颗,所以不够分。
答:不够分。
【点睛】本题可以先设这串葡萄有多少颗,然后利用除法求一个数的几分之几是多少求出两小动物要拿的颗数,再作进一步解答。
7.边长8米的正方形面积最大,是64平方米;长15米,宽1米的长方形面积最小,是15平方米
【分析】根据长方形的周长=(长+宽)×2,正方形的周长=边长×4,篱笆长32米,围成长方形的长宽和是16米,围成正方形的边长是8米。当长方形长宽差最小时,苗圃面积最大,也就是围成正方形时苗圃面积最大。当长方形的长宽差最大时,苗圃面积最小,此时长方形长15米,宽1米。根据长方形的面积=长×宽,正方形的面积=边长×边长解答。
【详解】32÷4=8(米)
8×8=64(平方米)
(15+1)×2
=16×2
=32(米)
15×1=15(平方米)
答:围成边长为8米的正方形时,面积最大,是64平方米。围成长15米宽1米的长方形时,面积最小,是15平方米。
【点睛】长方形的周长固定,长宽差越大,面积越小,长宽差越小,面积越大,若能围成正方形,正方形的面积最大。
8.大正方形的面积是121平方厘米,小正方形的面积是81平方厘米
【分析】根据题意画图如下:大正方形比小正方形的面积大的部分由3部分组成(黄色和黑色),其中2个黄色部分一样大,且黄色长方形的长为小正方形的边长,宽为2厘米,黑色部分是一个边长为2厘米的小正方形,面积是(2×2)平方厘米。所以小正方形的边长:(40-2×2)÷2÷2厘米,根据正方形的面积=边长×边长,求出小正方形的面积。再用小正方形的面积加上40平方厘米,求出大正方形的面积。
【详解】(40-2×2)÷2÷2
=(40-4)÷2÷2
=36÷2÷2
=18÷2
=9(厘米)
9×9=81(平方厘米)
81+40=121(平方厘米)
答:大正方形的面积是121平方厘米,小正方形的面积是81平方厘米。
【点睛】本题考查正方形面积公式的应用,关键是根据题意,画出图,帮助我们分析题中面积之间的关系。
9.24个
【分析】剩下的桃子总数等于原来2箱的桃子数,那么取走的桃子数就等于原来4箱的桃子数。用16乘6求出4箱桃子的总个数,再除以4即可求出原来每箱桃子的个数。
【详解】6-2=4(个)
16×6=96(个)
96÷4=24(个)
答:原来每箱桃子有24个。
【点睛】解答此题的关键是明确取走的桃子数就等于原来4箱的桃子数。
10.60位
【分析】用16乘4的积再减去4即可求出这个舞台上共有多少位小演员,据此解答。
【详解】16×4-4
=64-4
=60(位)
答:这个舞台上共有60位小演员。
【点睛】本题考查了正方形的周长公式,学生应熟练掌握并灵活运用。
11.150级
【分析】根据“哥哥每分钟走20级,结果哥哥5分钟到达楼上,”可以求出哥哥走的扶梯的个数,列式为:20×5=100级;根据“妹每分钟走15级,妹6分钟到达楼上”可以求出妹妹走的扶梯的个数,列式为:15×6=90级;再根据哥哥和妹妹走的扶梯的个数,可以求出自动扶梯的速度为:(100-90)÷(6-5)=10级;由于人和扶梯是同向运动的所以自动扶梯可见部分的个数为:(20+10)×5=150级,问题得解。
【详解】自动扶梯的速度为:
(20×5-15×6)÷(6-5)
=(100-90)÷1
=10(级)
自动扶梯可见部分的个数为:
(20+10)×5
=30×5
=150(级)
答:该自动扶梯有150级可见扶梯。
【点睛】此题考查的是和差问题,要理解上楼的速度可以分为两部分:一部分是兄妹的自己的速度,另一部分是自动扶梯的速度,所以利用和差知识求出自动扶梯的速度是本题的关键。
12.51厘米和49厘米;99厘米和1厘米
【分析】长方形的周长一定的情况下,长与宽越接近,它的面积越大,反之它的面积就越小,据此解答。
【详解】200÷2=100(厘米)
100=51+49,当长和宽分别是51厘米和49厘米时,面积最大。
100=1+99,当长和宽分别是99厘米和1厘米时,面积最小。
答:当长和宽分别是51厘米和49厘米时,面积最大。当长和宽分别是99厘米和1厘米时,面积最小。
【点睛】此题主要考查了长方形周长一定时,长和宽的长度与长方形面积之间的关系;长与宽的差越小它的面积就越大。
13.长方形;16平方厘米;20厘米
【分析】根据题意可知,要从一个长10厘米、宽8厘米的长方形上剪下一个最大的正方形,这个正方形的边长等于长方形的宽,即8厘米;剩下的部分是一个长8厘米、宽(10-8)厘米的长方形;再根据长方形面积=长×宽、长方形周长=(长+宽)×2,即可求剩下部分的面积和周长。
【详解】根据题意可知,剪下的正方形的边长是8厘米,剩下部分是一个长8厘米、宽(10-8)厘米的长方形。
8×(10-8)
=8×2
=16(平方厘米)
[8+(10-8)]×2
=[8+2]×2
=10×2
=20(厘米)
答:剩下部分是一个长8厘米、宽2厘米的长方形,它的面积是16平方厘米,周长是20厘米。
【点睛】确定剪下的正方形的边长是解答此题的关键。
14.10小时
【分析】根据题意可得,29元超过了5元,说明停车时间超过了2小时;先算出超过2小时的部分所花的钱数,再除以3元,即可求出超过2小时的部分是多少小时,再加上2小时就是总时间,据此解答即可。
【详解】(29-5)÷3+2
=24÷3+2
=8+2
=10(小时)
答:他最多停车10小时。
【点睛】此题考查了整数的四则混合运算,关键是求出超过2小时的费用和时间即可。
15.96平方米
【分析】长方形的面积=长×宽,先假设增加的是长,然后根据增加的面积求出原来长方形的宽,再根据增加的宽,求出原来长方形的长,最后再求出原来长方形空地的面积即可。
【详解】48÷6=8(米)
48÷4=12(米)
12×8=96(平方米)
答:原来长方形空地的面积是96平方米。
【点睛】熟练掌握长方形面积的实际运用是解答此题的关键。
16.三点零零九
【分析】先把小马虎读错的数写出来,再根据小数的读法进一步推出原来的小数即可。
【详解】三千零九写作:3009,原来的小数读出来要读两个零,所以正确的小数是3.009,故读作三点零零九。
答:正确的读法是三点零零九。
【点睛】熟练掌握小数的读写知识是解答本题的关键。
17.80平方米
【分析】根据长方形的周长公式:C=(a+b)÷2,那么a+b=C÷2,据此求出长与宽的和,当长与宽的差越小时,长方形的面积就越多,由此可以求出长与宽,然后根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】36÷2=18(米)
18=17+1=16+2=15+3=14+4=13+5=12+6=11+7=10+8
10×8=80(平方米)
答:围成菜园的面积最大是80平方米。
【点睛】此题主要考查长方形的周长公式、面积公式的灵活运用,关键是熟记公式。
18.熊、猪和鹿可以一起过桥,牛、猪和鹿可以一起过桥。
【分析】根据题意可知,这座桥限重1吨,也就是1000千克,在这4种动物中,看哪几种动物合起来等于或小于1吨,就可以一起过桥,据此解答。
【详解】1吨=1000千克,
480+190+150=820(千克)
600+190+150=940(千克)
答:熊、猪和鹿可以一起过桥,牛、猪和鹿可以一起过桥。
【点睛】此题考查的目的是理解掌握质量单位吨与千克之间的进率及换算,以及整数加法的计算法则、整数大小比较的方法及应用。
19.(1)
到站情况 里程/千米
B站﹣C站 158
C站﹣D站 126
D站﹣E站 694
(2)1956千米
(3)从C站到E站的路程长,长536千米
【分析】(1)B站到C站的里程=A站到C站的里程-A站到B站的里程;C站到D站的里程=A站到D站的里程- A站到C站的里程;D站到E站的里程=A站到E站的里程-A站到D站的里程,据此代入数据作答即可.
(2)从B站到E站一个来回的距离=(A站到E站的里程- A站到B站的里程)×2,据此代入数据作答即可;
(3)C站到E站的里程=A站到E站的里程-A站到C站的里程,B站到D站的里程=A站到D站的里程-A站到B站的里程,哪个数大说明哪段路长,长出的千米数=远的那段路程的长度-短的那段路程的长度,据此代入数据作答即可.
【详解】(1)B站﹣C站:322﹣164=158(千米),
C站﹣D站:448﹣322=126(千米),
D站﹣E站:1142﹣448=694(千米),
(2)(1142﹣164)×2
=978×2
=1956(千米)
答:从B站到E站一个来回有1956千米.
(3)C站﹣E站:1142﹣322=820(千米)
B站﹣D站:448﹣164=284(千米)
820﹣284=536(千米)
答:从C站到E站的路程长,长536千米.
20.30米
【分析】因为它们减去相同的1段,差是不变的,一直是93-51=42(米),红彩带是黄彩带的3倍,所以黄彩带剩下的部分就是42÷(3-1)=21米,减去的部分就用黄彩带总的长度减去剩下的部分就可以得出答案。
【详解】根据分析:
93-51=42(米)
42÷(3-1)
=42÷2
=21(米)
51-21=30(米)
答:两条彩带各减去30米。
【点睛】本题主要考查的是整数的复合应用题,对于这类问题就要根据相互关联的数量关系找出已知数量和未知数量的联系,先解答一个或几个中间问题,也就是把它先分解成几个简单应用题,然后再根据它们的联系依次列式并求解。
21.(1)东面;170米
(2)3170米
【分析】算出每分钟走65米,18分钟走的路程为65×18=1170米;
(1)小华家离学校1千米,向东走1170米,超过到学校的距离,就到了学校的东面;
(2)小华家离公园2千米,向北走1170米,将小华家与图书馆的距离和小华家到公园的距离加起来即可。
【详解】(1)65×18=1170(米)
1千米=1000米
1000<1170
超过了学校,现在在学校东面
1170-1000=170(米)
答:现在在学校东面,距离学校170米。
(2)2千米=2000米
1170+2000=3170(米)
答:图书馆与公园的距离是3170米。
【点睛】此题考查行程问题和方向的辨别,注意结合图形,根据数据和方向确定位置。
22.650米或50米
【分析】如果他们两人在学校的两侧,用加法解答,小芳每分钟行60米,5分钟到家,小芳家离学校的距离为60×5,同理,小军家离学校的距离是70×5,要求小芳家到小军家的距离,把这两部分加起来即可;如果他们两家在学校的同一侧,根据减法的意义,用减法解答。
【详解】60×5+70×5
=300+350
=650(米)
70×5-60×5
=350-300
=50(米)
答:小芳和小军两家相距650米或50米。
【点睛】此题解答关键是明确:他们两家在学校的同一侧,还是在学校的两侧。
23.294
【分析】27比21多6,乘积多了84,说明乘积多了第一个因数的6倍,这样用84除以6即可求出第一个因数,然后用乘法计算出正确的积即可。
【详解】27-21=6
84÷6=14
21×14=294
答:正确的积是294。
24.8352
【分析】根据整数乘法计算法则,必须先使十位数最大,且使较小的十位数字后面的个位数较大,才能使它和较大的两位数相乘,确保乘积最大。
【详解】96×87=8352
答:它们的积最大应是8352。
【点睛】关键明白,要使这两个数的积最大,首先必须这两个数最大。
25.15块
【详解】20÷2+(20-20÷2)÷2=15(块)
26.0.8千克
【分析】根据题意,乙比甲重0.3千克,也就是说甲比乙少了0.3千克,丙比乙又多0.5千克,这样甲就比丙少了0.3+0.5千克,由此解答。
【详解】0.3+0.5=0.8(千克)
答:甲比丙轻0.8千克。
【点睛】解答本题的关键是找到乙作为甲和丙的中间参考量,用他们与乙的轻重关系来得出答案。
27.6.2元
【分析】王成给妹妹3元钱后,王成的钱减少了3元,这样两人的差就缩小了(3+3)元,再加上现在的相差的钱数,就是原来两人相差的钱数,由此求解。
【详解】3+3+0.2
=6+0.2
=6.2(元)
答:原来妹妹比王成少6.2元。
【点睛】解决本题关键是理解两人的钱数差减少了2个3元,而不是1个3元,然后再进一步求解。
28.5千克;1.3千克
【详解】3.8+3.8=7.6(千克)
桶重:7.6-6.3=1.3(千克)
油重:6.3-1.3=5(千克)
第12页,共12页
第11页,共12页
同课章节目录
