苏教版2025年四年级下学期数学(期末巩固)暑假伴学营分类专训系列:图形计算题(含解析)
文档属性
| 名称 | 苏教版2025年四年级下学期数学(期末巩固)暑假伴学营分类专训系列:图形计算题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 567.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览


文档简介
苏教版2025年四年级下学期数学(期末巩固)暑假伴学营分类专训系列:图形计算题
学校:___________姓名:___________班级:___________
计算题
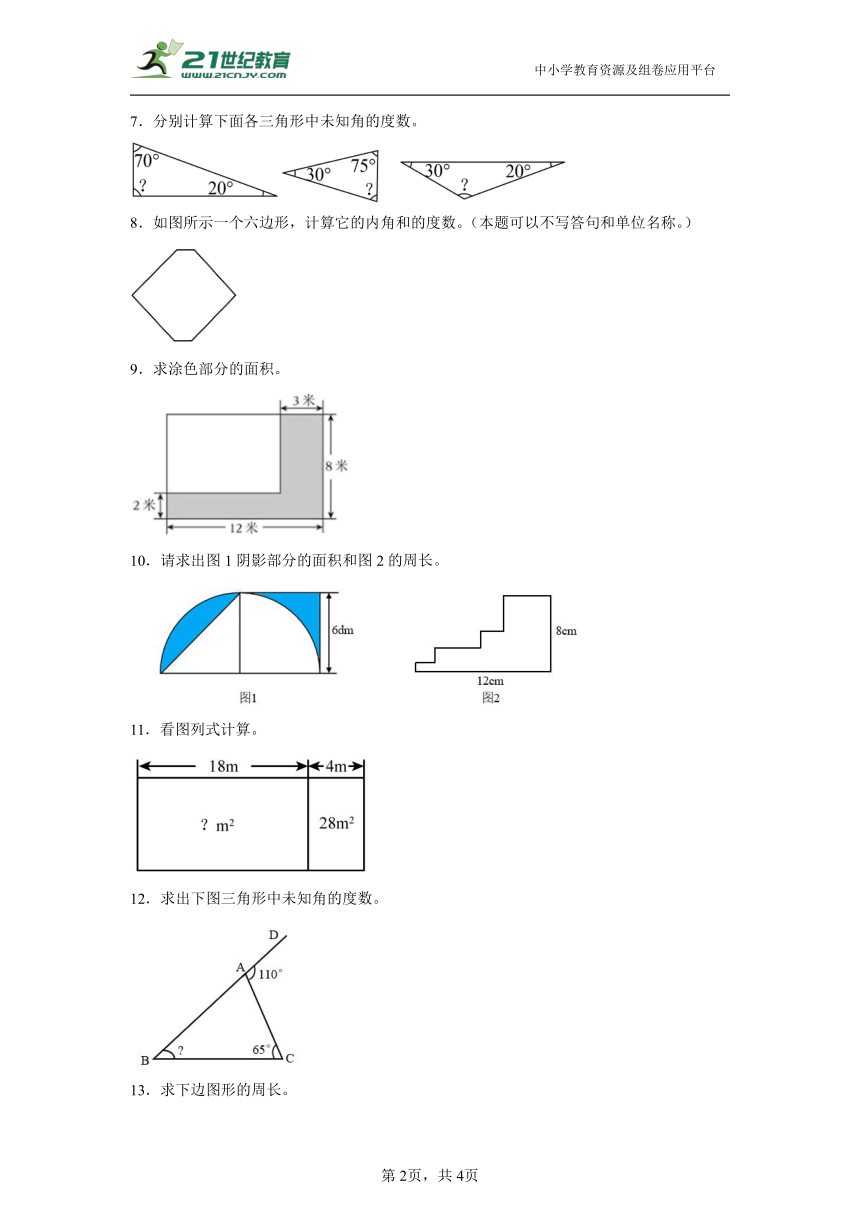
1.计算下面图形的周长。(单位:cm)
2.用两种方法计算下图中大长方形的面积。(单位:米)
3.在下图的三角形中,已知∠1=65°,∠2=60°,请求出∠4的度数。
4.求出四边形和六边形的内角和。
5.根据三角形的内角和是180°,你能求出四边形的内角和吗?
6.如图,计算梯形中∠1、∠2、∠3的度数。
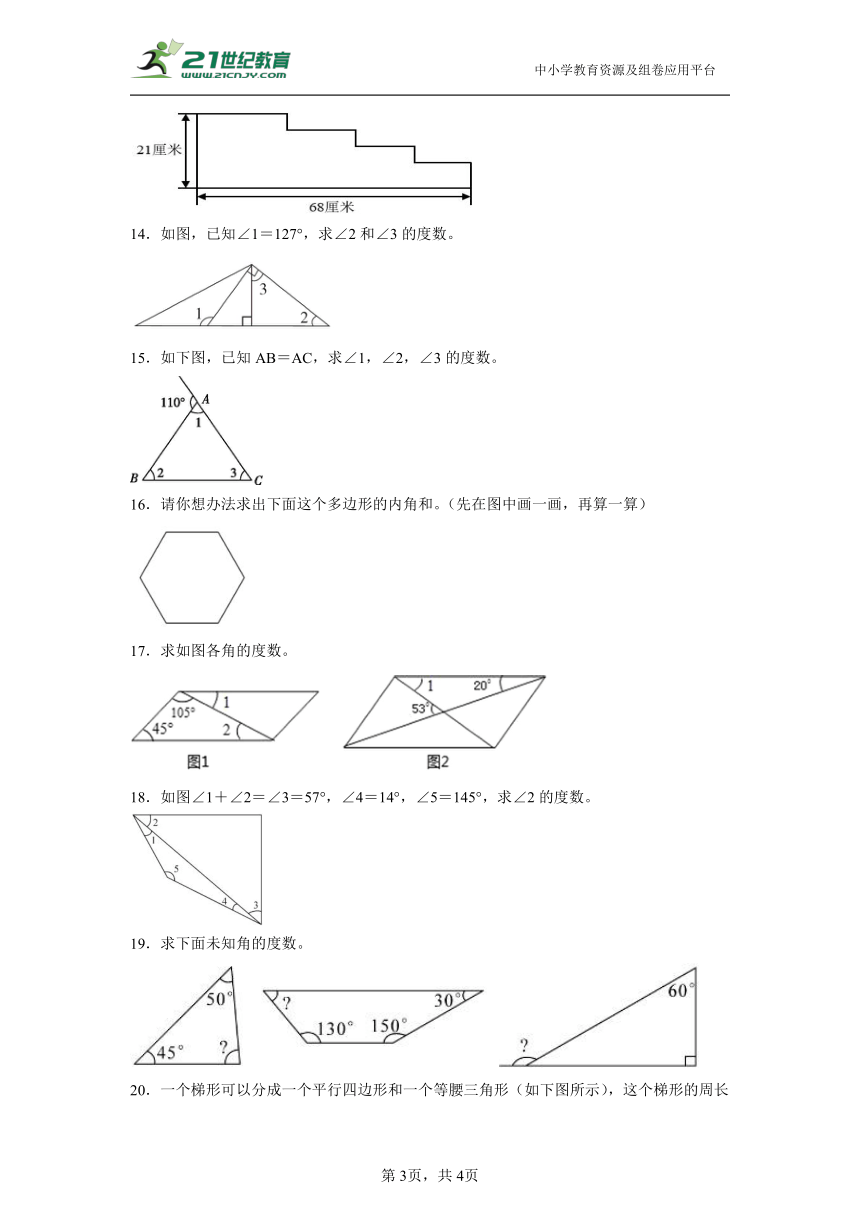
7.分别计算下面各三角形中未知角的度数。
8.如图所示一个六边形,计算它的内角和的度数。(本题可以不写答句和单位名称。)
9.求涂色部分的面积。
10.请求出图1阴影部分的面积和图2的周长。
11.看图列式计算。
12.求出下图三角形中未知角的度数。
13.求下边图形的周长。
14.如图,已知∠1=127°,求∠2和∠3的度数。
15.如下图,已知AB=AC,求∠1,∠2,∠3的度数。
16.请你想办法求出下面这个多边形的内角和。(先在图中画一画,再算一算)
17.求如图各角的度数。
18.如图∠1+∠2=∠3=57°,∠4=14°,∠5=145°,求∠2的度数。
19.求下面未知角的度数。
20.一个梯形可以分成一个平行四边形和一个等腰三角形(如下图所示),这个梯形的周长是多少厘米?
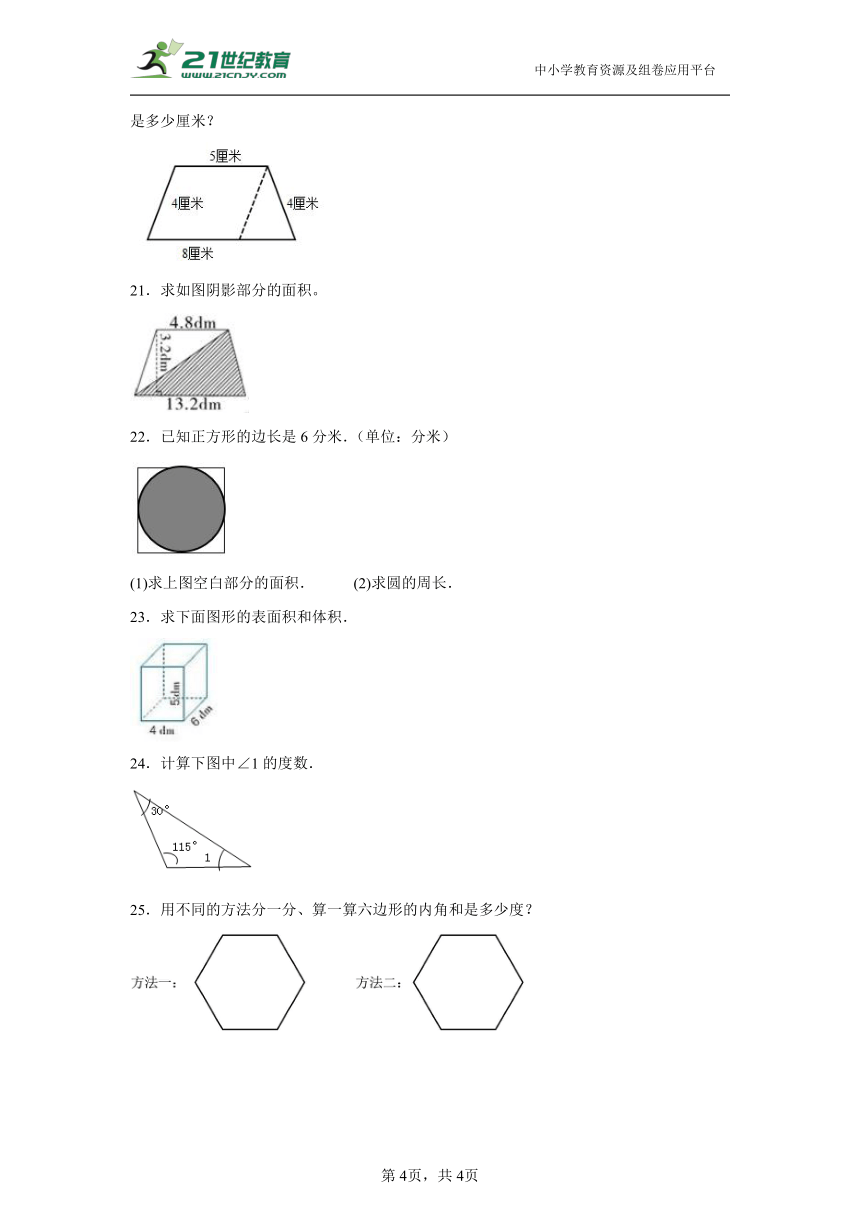
21.求如图阴影部分的面积。
22.已知正方形的边长是6分米.(单位:分米)
(1)求上图空白部分的面积. (2)求圆的周长.
23.求下面图形的表面积和体积.
24.计算下图中∠1的度数.
25.用不同的方法分一分、算一算六边形的内角和是多少度?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第2页,共4页
第3页,共4页
参考答案
1.60cm
【分析】
如图所示,将这个图形边缘往两侧平移,这个图形的周长可以看作是一个长为20cm,宽为(4+6)cm的长方形周长,根据长方形的周长=(长+宽)×2,代入相应数值计算,即可解答。
【详解】(20+4+6)×2
=30×2
=60(cm)
所以这个图形的周长是60cm。
2.312平方米
【分析】解法一:观察图可以发现,大长方形由两个小长方形组成,大长方形的长等于左边长方形的长加上右边长方形的长,宽为12米,根据长方形的面积=长×宽,即可求出大长方形的面积。
解法二:观察图可以发现,大长方形由两个小长方形组成,根据长方形的面积=长×宽,分别求出左右两边小长方形的面积,再将左右两边小长方形的面积相加,即可求出大长方形的面积。
【详解】解法一:
(16+10)×12
=26×12
=312(平方米)
解法二:
16×12+10×12
=192+120
=312(平方米)
所以大长方形的面积为312平方米。
3.125°
【分析】已知三角形的三个内角和是180°,三个内角有两个已经知道,要求未知的那一个内角,用180°连续减去两个内角的度数即可,据此可求出∠3的度数,又因为∠3和∠4组成一个平角,用180°减去∠3的度数就是∠4的度数。
【详解】∠3=180°-65°-60°=115°-60°=55°
∠4=180°-55°=125°
4.四边形360°;六边形720°
【分析】根据过同一顶点作出的对角线把多边形分成的三角形的个数,再利用三角形的内角和等于180°即可计算出四边形、六边形的内角和。
【详解】四边形分成2个三角形,则四边形的内角和是:180°×2=360°
六边形分成4个三角形,则六边形的内角和是:180°×4=720°
5.360°
【分析】三角形内角和是180°,图中的四边形由两个三角形组成,则用180°×2即可求出四边形的内角和。
【详解】180°×2=360°
四边形的内角和是360°。
6.∠1=;∠2=;∠3=
【分析】根据三角形的内角和等于180度,直角是90度,可以求出∠1的度数;∠2的度数等于90度角减去∠1的度数;根据三角形的内角和等于180度,可知∠3的度数等于180度减130度再减∠2,据此解答即可。
【详解】
=
=
=
=
=
所以。
7.90°;75°;130°;
【分析】三角形的内角和是180°,因此用三角形的内角和减去另外两个角的度数之和,即可得到第三个角的度数,依此计算。
【详解】180°-(70°+20°)
=180°-90°
=90°
180°-(30°+75°)
=180°-105°
=75°
180°-(30°+20°)
=180°-50°
=130°
8.720°
【分析】
根据多边形内角和的计算方法,从六边形的一个顶点向相对的顶点连线,把六边形分成4个三角形(如图),每个三角形的内角和是180°,所以六边形的内角和=180°×4。据此解答。
【详解】根据分析可知:
180°×4=720°
所以,六边形的内角和的度数是720°。
9.42平方米
【分析】涂色部分的面积=大长方形的面积-小长方形的面积,长方形的面积=长×宽,小长方形的长=(12-3)米,小长方形的宽=(8-2)米,据此列式解答即可。
【详解】12-3=9(米)
8-2=6(米)
涂色部分的面积:
12×8-9×6
=96-54
=42(平方米)
10.18dm2;40cm
【分析】(1)根据半圆是轴对称图形,沿对称轴折叠可以发现,阴影部分的面积等于以6dm为边长的正方形面积的一半;
(2)通过平移,其周长就是长12cm、宽8cm的长方形的周长。
【详解】(1)6×6÷2
=36÷2
=18(dm2)
图1阴影部分的面积是18dm2。
(2)(12+8)×2
=20×2
=40(cm)
图2周长是40cm。
11.126m2
【分析】长方形的面积=长×宽,则长方形的长=面积÷宽,用长方形的面积28m2除以长方形的宽4m即可算出右边小长方形的长是(28÷4)m,右边小长方形的长就是左边长方形的宽,根据长方形的面积=长×宽,把数据代入公式计算即可。
【详解】28÷4=7(m)
18×7=126(m2)
12.45°
【分析】1平角=180°,180°减110°即可求出与110°角相邻的角,这个角是这个三角形的一个内角,三角形的内角和是180°,180°减三角形的两个内角即可求出∠B的度数。
【详解】180°-110°=70°
180°-70°-65°
=110°-65°
=45°
【点睛】1平角=180°,此题的重点是先求出与110°角相邻的角的度数。
13.178厘米
【分析】
,如图所示,将图形的边平移后可知,图形的周长等于长68厘米,宽21厘米的长方形的周长,根据长方形的周长=(长+宽)×2;代入数据,即可解答。
【详解】(68+21)×2
=89×2
=178(厘米)
14.∠2=37°;∠3=53°
【分析】如下图,∠4等于180°减∠1,∠2和∠4是直角三角形中的两个锐角,所以∠2等于90°减∠4,∠3和∠2也是直角三角形的两个锐角,所以∠3等于90°减∠2,据此即可解答。
【详解】∠4=180°-127°=53°
∠2=90°-∠4
=90°-53°
=37°
∠3=90°-∠2
=90°-37°
=53°
15.70°;55°;55°
【分析】三角形中,AB=AC,则这个角是等腰三角形。∠2=∠3。∠1和110°的角组成一个平角,则∠1=180°-110°。根据三角形的内角和为180°可知,∠2=∠3=(180°-∠1)÷2。
【详解】∠1=180°-110°=70°
(180°-70°)÷2
=110°÷2
=55°
则∠2=∠3=55°。
16.720°
【分析】将这个多边形分成4个三角形。根据三角形的内角和为180°可知,这个多边形的内角和为180°×4。
【详解】
180°×4=720°
则这个多边形的内角和是720°。
17.图1:∠1=∠2=30°;
图2:∠1=33°
【分析】(1)如下图,根据平行四边形的特征,∠1=∠2,再根据三角形的内角和是180°求出∠1和∠2的度数;
(2)如下图,根据∠2+53°=180°,先求出∠2的度数,再根据∠1+∠2+20°=180°,即可求出∠1的度数。
【详解】
图1:∠1=∠2=180°-105°-45°=30°
图2:∠2=180°-53°=127°
所以∠1=180°-127°-20°=33°
【点睛】本题主要考查三角形内角和定理的灵活应用,解题的关键是要结合图形,找到各个角之间的关系,逐步进行解答。
18.36°
【分析】三角形内角和是180°,因此可用180°减去∠4、∠5的度数计算出∠1的度数,然后用57°减去∠1的度数即可。
【详解】∠1=180°-∠4-∠5
=180°-14°-145°
=166°-145°
=21°
∠2=57°-∠1
=57°-21°
=36°
19.85°;50°;150°
【分析】三角形内角和是180度,四边形内角和360度,据此求出未知角。
【详解】180°-45°-50°
=135°-50°
=85°
360°-130°-150°-30°
=230°-150°-30°
=80°-30°
=50°
180°-(90°-60°)
=180°-30°
=150°
【点睛】本题考查了三角形内角和,计算时要仔细。
20.21厘米
【分析】封闭图形一周的长度叫做周长由此解答即可。
【详解】5+8+4+4
=13+4+4
=17+4
=21(厘米)
【点睛】本题考查梯形的周长,计算时要细心。
21.21.12dm2
【分析】阴影部分的面积看作是底为13.2dm,高是3.2dm的三角形的面积,根据三角形的面积=底×高÷2,解答即可。
【详解】13.2×3.2÷2
=42.24÷2
=21.12(dm2)
答:如图阴影部分的面积为21.12dm2。
22.(1)6×6-3.14×3×3=7.74(平方分米)
(2)2×3×3.14=18.84(平方分米)
【详解】略
23.表面积:4×5×2+5×6×2+4×6×2=148()
体积:4×5×6=120()
【详解】略
24.180°-115°-30°= 35°;
【详解】本题考查学生对三角形内角的认识.分析三个图可知,都是已知三角形的两个内角,求第三个内角的度数.根据三角形内角和等于180°,∠1的度数应该是用180°分别减去另外两个角的度数就可以了,其中(2)小题中的三角形是直角三角形,也就是有一个角是90°.
25.图见详解;720°
【分析】三角形内角和是180°,可以将六边形分成几个三角形,用180°乘三角形的个数,即可求出六边形的内角和是多少度;先找出六边形的中心点,将六边形所有的顶点与这个中心点连接,则分成了几个三角形,用三角形的个数乘180°,再减去中心点所形成的周角度数,即可求出六边形的内角和是多少度。
【详解】
方法一:(画法不唯一)
180°×4=720°
方法二:(画法不唯一)
180°×6-360°
=1080°-360°
=720°
答:六边形的内角和是720°。
第8页,共9页
第9页,共9页
学校:___________姓名:___________班级:___________
计算题
1.计算下面图形的周长。(单位:cm)
2.用两种方法计算下图中大长方形的面积。(单位:米)
3.在下图的三角形中,已知∠1=65°,∠2=60°,请求出∠4的度数。
4.求出四边形和六边形的内角和。
5.根据三角形的内角和是180°,你能求出四边形的内角和吗?
6.如图,计算梯形中∠1、∠2、∠3的度数。
7.分别计算下面各三角形中未知角的度数。
8.如图所示一个六边形,计算它的内角和的度数。(本题可以不写答句和单位名称。)
9.求涂色部分的面积。
10.请求出图1阴影部分的面积和图2的周长。
11.看图列式计算。
12.求出下图三角形中未知角的度数。
13.求下边图形的周长。
14.如图,已知∠1=127°,求∠2和∠3的度数。
15.如下图,已知AB=AC,求∠1,∠2,∠3的度数。
16.请你想办法求出下面这个多边形的内角和。(先在图中画一画,再算一算)
17.求如图各角的度数。
18.如图∠1+∠2=∠3=57°,∠4=14°,∠5=145°,求∠2的度数。
19.求下面未知角的度数。
20.一个梯形可以分成一个平行四边形和一个等腰三角形(如下图所示),这个梯形的周长是多少厘米?
21.求如图阴影部分的面积。
22.已知正方形的边长是6分米.(单位:分米)
(1)求上图空白部分的面积. (2)求圆的周长.
23.求下面图形的表面积和体积.
24.计算下图中∠1的度数.
25.用不同的方法分一分、算一算六边形的内角和是多少度?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第2页,共4页
第3页,共4页
参考答案
1.60cm
【分析】
如图所示,将这个图形边缘往两侧平移,这个图形的周长可以看作是一个长为20cm,宽为(4+6)cm的长方形周长,根据长方形的周长=(长+宽)×2,代入相应数值计算,即可解答。
【详解】(20+4+6)×2
=30×2
=60(cm)
所以这个图形的周长是60cm。
2.312平方米
【分析】解法一:观察图可以发现,大长方形由两个小长方形组成,大长方形的长等于左边长方形的长加上右边长方形的长,宽为12米,根据长方形的面积=长×宽,即可求出大长方形的面积。
解法二:观察图可以发现,大长方形由两个小长方形组成,根据长方形的面积=长×宽,分别求出左右两边小长方形的面积,再将左右两边小长方形的面积相加,即可求出大长方形的面积。
【详解】解法一:
(16+10)×12
=26×12
=312(平方米)
解法二:
16×12+10×12
=192+120
=312(平方米)
所以大长方形的面积为312平方米。
3.125°
【分析】已知三角形的三个内角和是180°,三个内角有两个已经知道,要求未知的那一个内角,用180°连续减去两个内角的度数即可,据此可求出∠3的度数,又因为∠3和∠4组成一个平角,用180°减去∠3的度数就是∠4的度数。
【详解】∠3=180°-65°-60°=115°-60°=55°
∠4=180°-55°=125°
4.四边形360°;六边形720°
【分析】根据过同一顶点作出的对角线把多边形分成的三角形的个数,再利用三角形的内角和等于180°即可计算出四边形、六边形的内角和。
【详解】四边形分成2个三角形,则四边形的内角和是:180°×2=360°
六边形分成4个三角形,则六边形的内角和是:180°×4=720°
5.360°
【分析】三角形内角和是180°,图中的四边形由两个三角形组成,则用180°×2即可求出四边形的内角和。
【详解】180°×2=360°
四边形的内角和是360°。
6.∠1=;∠2=;∠3=
【分析】根据三角形的内角和等于180度,直角是90度,可以求出∠1的度数;∠2的度数等于90度角减去∠1的度数;根据三角形的内角和等于180度,可知∠3的度数等于180度减130度再减∠2,据此解答即可。
【详解】
=
=
=
=
=
所以。
7.90°;75°;130°;
【分析】三角形的内角和是180°,因此用三角形的内角和减去另外两个角的度数之和,即可得到第三个角的度数,依此计算。
【详解】180°-(70°+20°)
=180°-90°
=90°
180°-(30°+75°)
=180°-105°
=75°
180°-(30°+20°)
=180°-50°
=130°
8.720°
【分析】
根据多边形内角和的计算方法,从六边形的一个顶点向相对的顶点连线,把六边形分成4个三角形(如图),每个三角形的内角和是180°,所以六边形的内角和=180°×4。据此解答。
【详解】根据分析可知:
180°×4=720°
所以,六边形的内角和的度数是720°。
9.42平方米
【分析】涂色部分的面积=大长方形的面积-小长方形的面积,长方形的面积=长×宽,小长方形的长=(12-3)米,小长方形的宽=(8-2)米,据此列式解答即可。
【详解】12-3=9(米)
8-2=6(米)
涂色部分的面积:
12×8-9×6
=96-54
=42(平方米)
10.18dm2;40cm
【分析】(1)根据半圆是轴对称图形,沿对称轴折叠可以发现,阴影部分的面积等于以6dm为边长的正方形面积的一半;
(2)通过平移,其周长就是长12cm、宽8cm的长方形的周长。
【详解】(1)6×6÷2
=36÷2
=18(dm2)
图1阴影部分的面积是18dm2。
(2)(12+8)×2
=20×2
=40(cm)
图2周长是40cm。
11.126m2
【分析】长方形的面积=长×宽,则长方形的长=面积÷宽,用长方形的面积28m2除以长方形的宽4m即可算出右边小长方形的长是(28÷4)m,右边小长方形的长就是左边长方形的宽,根据长方形的面积=长×宽,把数据代入公式计算即可。
【详解】28÷4=7(m)
18×7=126(m2)
12.45°
【分析】1平角=180°,180°减110°即可求出与110°角相邻的角,这个角是这个三角形的一个内角,三角形的内角和是180°,180°减三角形的两个内角即可求出∠B的度数。
【详解】180°-110°=70°
180°-70°-65°
=110°-65°
=45°
【点睛】1平角=180°,此题的重点是先求出与110°角相邻的角的度数。
13.178厘米
【分析】
,如图所示,将图形的边平移后可知,图形的周长等于长68厘米,宽21厘米的长方形的周长,根据长方形的周长=(长+宽)×2;代入数据,即可解答。
【详解】(68+21)×2
=89×2
=178(厘米)
14.∠2=37°;∠3=53°
【分析】如下图,∠4等于180°减∠1,∠2和∠4是直角三角形中的两个锐角,所以∠2等于90°减∠4,∠3和∠2也是直角三角形的两个锐角,所以∠3等于90°减∠2,据此即可解答。
【详解】∠4=180°-127°=53°
∠2=90°-∠4
=90°-53°
=37°
∠3=90°-∠2
=90°-37°
=53°
15.70°;55°;55°
【分析】三角形中,AB=AC,则这个角是等腰三角形。∠2=∠3。∠1和110°的角组成一个平角,则∠1=180°-110°。根据三角形的内角和为180°可知,∠2=∠3=(180°-∠1)÷2。
【详解】∠1=180°-110°=70°
(180°-70°)÷2
=110°÷2
=55°
则∠2=∠3=55°。
16.720°
【分析】将这个多边形分成4个三角形。根据三角形的内角和为180°可知,这个多边形的内角和为180°×4。
【详解】
180°×4=720°
则这个多边形的内角和是720°。
17.图1:∠1=∠2=30°;
图2:∠1=33°
【分析】(1)如下图,根据平行四边形的特征,∠1=∠2,再根据三角形的内角和是180°求出∠1和∠2的度数;
(2)如下图,根据∠2+53°=180°,先求出∠2的度数,再根据∠1+∠2+20°=180°,即可求出∠1的度数。
【详解】
图1:∠1=∠2=180°-105°-45°=30°
图2:∠2=180°-53°=127°
所以∠1=180°-127°-20°=33°
【点睛】本题主要考查三角形内角和定理的灵活应用,解题的关键是要结合图形,找到各个角之间的关系,逐步进行解答。
18.36°
【分析】三角形内角和是180°,因此可用180°减去∠4、∠5的度数计算出∠1的度数,然后用57°减去∠1的度数即可。
【详解】∠1=180°-∠4-∠5
=180°-14°-145°
=166°-145°
=21°
∠2=57°-∠1
=57°-21°
=36°
19.85°;50°;150°
【分析】三角形内角和是180度,四边形内角和360度,据此求出未知角。
【详解】180°-45°-50°
=135°-50°
=85°
360°-130°-150°-30°
=230°-150°-30°
=80°-30°
=50°
180°-(90°-60°)
=180°-30°
=150°
【点睛】本题考查了三角形内角和,计算时要仔细。
20.21厘米
【分析】封闭图形一周的长度叫做周长由此解答即可。
【详解】5+8+4+4
=13+4+4
=17+4
=21(厘米)
【点睛】本题考查梯形的周长,计算时要细心。
21.21.12dm2
【分析】阴影部分的面积看作是底为13.2dm,高是3.2dm的三角形的面积,根据三角形的面积=底×高÷2,解答即可。
【详解】13.2×3.2÷2
=42.24÷2
=21.12(dm2)
答:如图阴影部分的面积为21.12dm2。
22.(1)6×6-3.14×3×3=7.74(平方分米)
(2)2×3×3.14=18.84(平方分米)
【详解】略
23.表面积:4×5×2+5×6×2+4×6×2=148()
体积:4×5×6=120()
【详解】略
24.180°-115°-30°= 35°;
【详解】本题考查学生对三角形内角的认识.分析三个图可知,都是已知三角形的两个内角,求第三个内角的度数.根据三角形内角和等于180°,∠1的度数应该是用180°分别减去另外两个角的度数就可以了,其中(2)小题中的三角形是直角三角形,也就是有一个角是90°.
25.图见详解;720°
【分析】三角形内角和是180°,可以将六边形分成几个三角形,用180°乘三角形的个数,即可求出六边形的内角和是多少度;先找出六边形的中心点,将六边形所有的顶点与这个中心点连接,则分成了几个三角形,用三角形的个数乘180°,再减去中心点所形成的周角度数,即可求出六边形的内角和是多少度。
【详解】
方法一:(画法不唯一)
180°×4=720°
方法二:(画法不唯一)
180°×6-360°
=1080°-360°
=720°
答:六边形的内角和是720°。
第8页,共9页
第9页,共9页
同课章节目录
