苏科版数学九年级下册 第7章 锐角三角函数 单元测试(含答案)
文档属性
| 名称 | 苏科版数学九年级下册 第7章 锐角三角函数 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 245.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 23:34:10 | ||
图片预览


文档简介
苏科版九年级下 第7章 锐角三角函数 单元测试
一.选择题(共12小题)
1.如图,在△ABC中,∠C=90°,AB=5,AC=4,则cosA的值是( )
A. B. C. D.
2.如图,在△ABC中,∠A=90°,AB=4,BC=5,则cosB等于( )
A. B. C. D.
3.如图,市政府准备修建一座高AB=5米的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为,则坡面AC的长度为( )
A. B. C. D.
4.在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,下列各式成立的是( )
A.sinB= B.cosB= C.tanB= D.tanB=
5.某兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为45°,沿同一坡面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底D处,斜面AB的坡度(或坡比)i=1:2.4,则大树CD的高度为( )
A.5米 B.12米 C.13米 D.18米
6.如图,滨海办公区东、西两栋办公楼的高度相等,且水平距离为30m.下午3时太阳光线与地面所成的角是35°.这时东楼二层离地3m的阳台与西楼的楼顶、太阳恰好在一条直线上,则这两栋办公楼的高度为( )
A.(30 tan35°)m B.(30 tan35°+3)m
C.(30 cos35°+3)m D.
7.如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
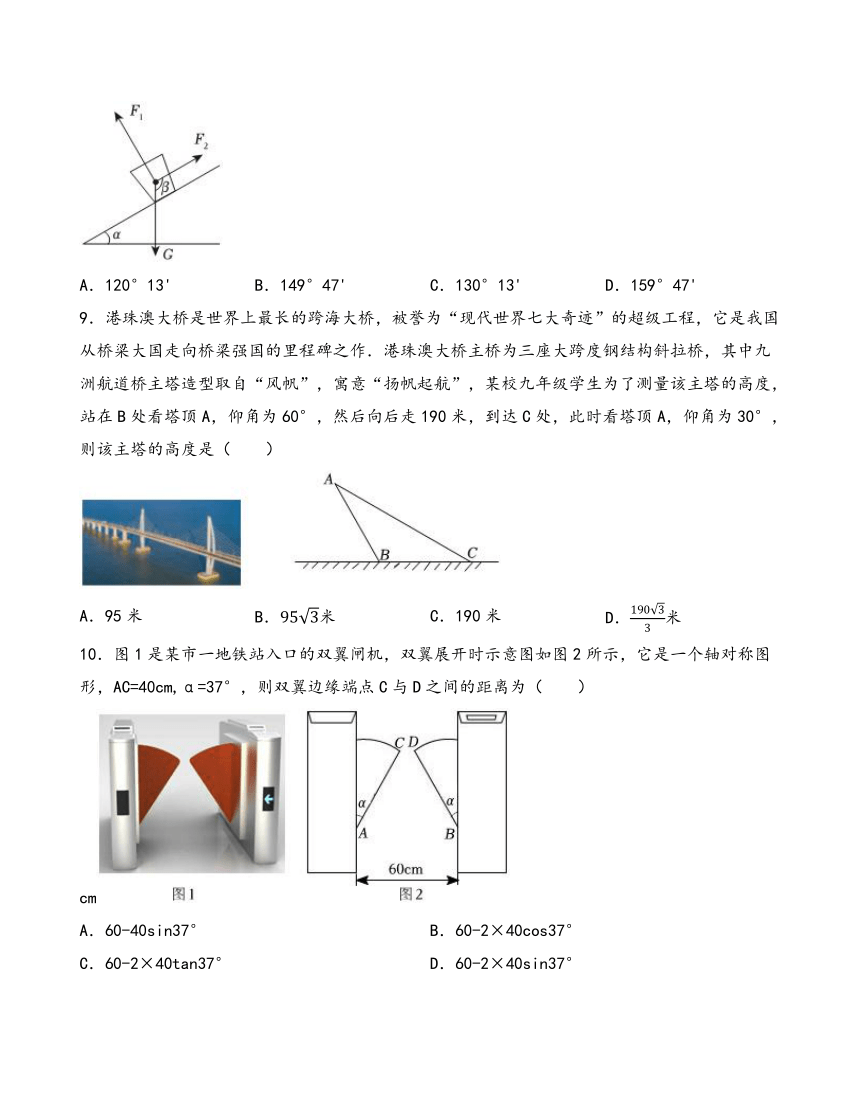
8.一个木块静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行,若斜面的坡角α=30°13',则摩擦力F2与重力G的夹角β的度数为( )
A.120°13' B.149°47' C.130°13' D.159°47'
9.港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
10.图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40cm,α=37°,则双翼边缘端点C与D之间的距离为( )cm
A.60-40sin37° B.60-2×40cos37°
C.60-2×40tan37° D.60-2×40sin37°
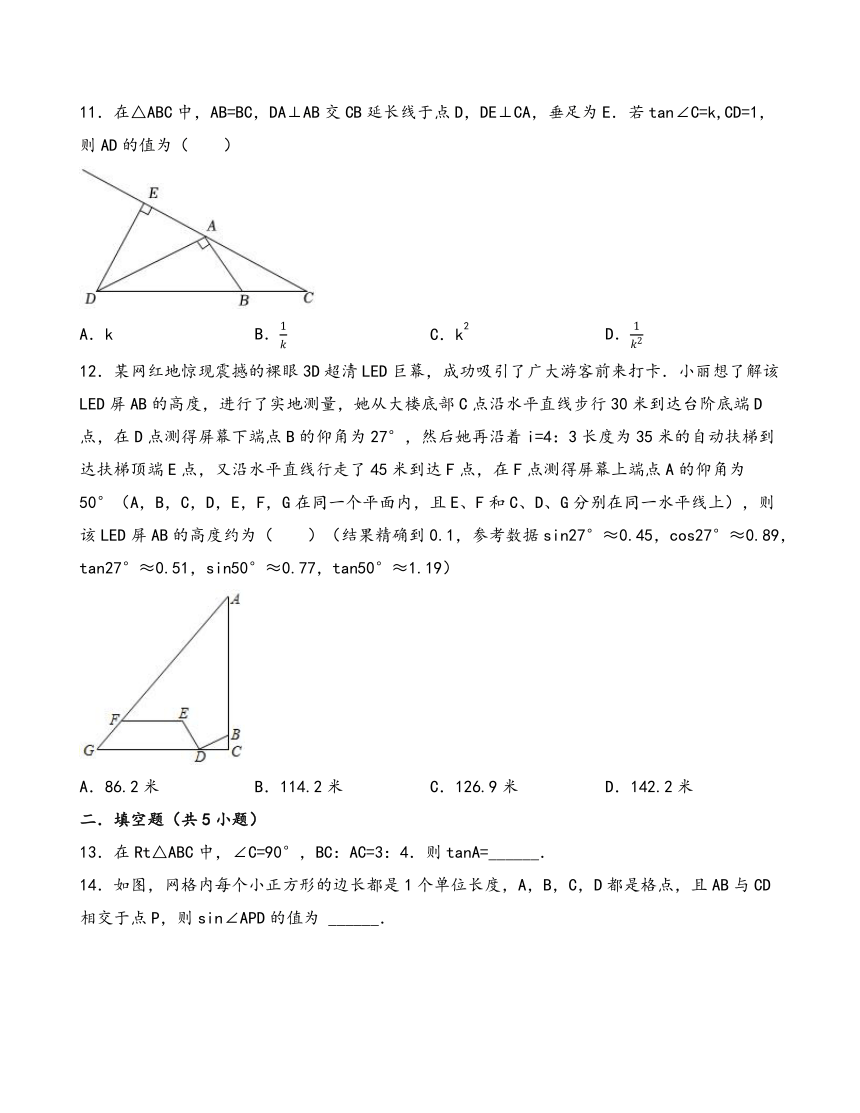
11.在△ABC中,AB=BC,DA⊥AB交CB延长线于点D,DE⊥CA,垂足为E.若tan∠C=k,CD=1,则AD的值为( )
A.k B. C.k2 D.
12.某网红地惊现震撼的裸眼3D超清LED巨幕,成功吸引了广大游客前来打卡.小丽想了解该LED屏AB的高度,进行了实地测量,她从大楼底部C点沿水平直线步行30米到达台阶底端D点,在D点测得屏幕下端点B的仰角为27°,然后她再沿着i=4:3长度为35米的自动扶梯到达扶梯顶端E点,又沿水平直线行走了45米到达F点,在F点测得屏幕上端点A的仰角为50°(A,B,C,D,E,F,G在同一个平面内,且E、F和C、D、G分别在同一水平线上),则该LED屏AB的高度约为( )(结果精确到0.1,参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin50°≈0.77,tan50°≈1.19)
A.86.2米 B.114.2米 C.126.9米 D.142.2米
二.填空题(共5小题)
13.在Rt△ABC中,∠C=90°,BC:AC=3:4.则tanA=______.
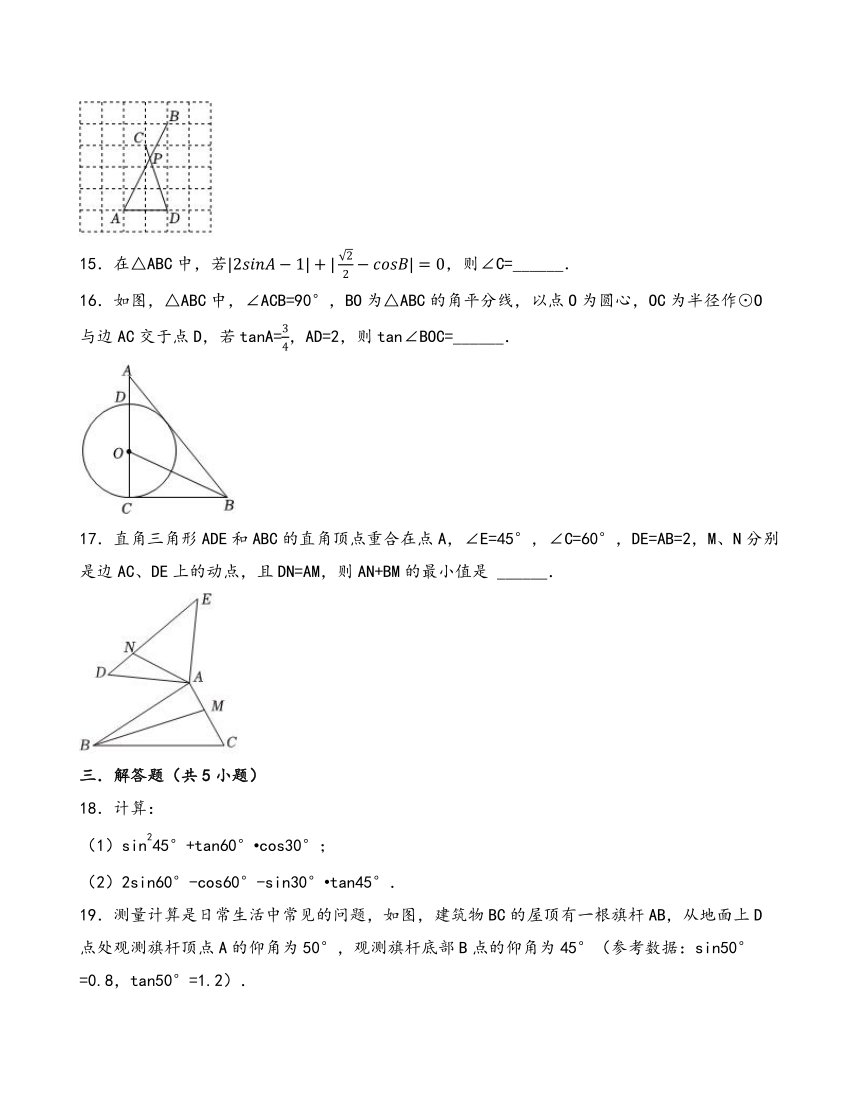
14.如图,网格内每个小正方形的边长都是1个单位长度,A,B,C,D都是格点,且AB与CD相交于点P,则sin∠APD的值为 ______.
15.在△ABC中,若,则∠C=______.
16.如图,△ABC中,∠ACB=90°,BO为△ABC的角平分线,以点O为圆心,OC为半径作⊙O与边AC交于点D,若tanA=,AD=2,则tan∠BOC=______.
17.直角三角形ADE和ABC的直角顶点重合在点A,∠E=45°,∠C=60°,DE=AB=2,M、N分别是边AC、DE上的动点,且DN=AM,则AN+BM的最小值是 ______.
三.解答题(共5小题)
18.计算:
(1)sin245°+tan60° cos30°;
(2)2sin60°-cos60°-sin30° tan45°.
19.测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°(参考数据:sin50°=0.8,tan50°=1.2).
(1)若已知CD=25米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=4米,求建筑物BC的高度.
20.2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的四边形空地.如图,已知AB=9m,BC=12m,CD=17m,AD=8m,技术人员在只有卷尺的情况下,通过测量某两点之间距离为15m,便快速确定了∠ABC=90°.
(1)请写出技术人员测量的是哪两点之间的距离,并说明他确定∠ABC=90°的理由;
(2)若平均每平方米空地的绿化费用为100元,试计算绿化这片空地共需花费多少元?
21.2025年是“健康体重管理年”,某健身俱乐部精准把握时代脉搏购进健身器械,如图(1)所示的健身器械为倒蹬机,使用方法为上身不动,腿部向前发力,双腿伸直之后再慢慢收回.图(2)为其抽象示意图,已知DE,DC在初始位置,DE=DC=60cm,点B,C,G,在同一直线上,AB⊥BG,∠A=46°,∠DCG=95°.
(1)当DE,DC在初始位置时,求点D到AC的距离;
(2)当双腿伸直后,点E,D分别从初始位置运动到点E′,D′,假设E′,D′,C三点共线,求此时点E上升的竖直高度.(结果精确到0.01cm,参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869,sin44°≈0.695,cos44°≈0.719,tan44°≈0.966)
22.综合与实践
【教材重现】北师大版九年级下册教科书第9页例2:如图1,一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01).图2是该情境建模后的图形.(本题不用解答)
实际上,当秋千向两边摆动时,由于受摩擦力等其他因素的影响,两边摆动的角度一定不相同.某兴趣小组去到公园进行实地探究,测量了若干数据.请解答下列问题:
(1)如图3,秋千没摆动时,秋千的踏板离地面是0.7m,将它往左拉1.5m,此时踏板离地面1.2m,求秋千链子OA的长度;
(2)如图4,在(1)的条件下,释放踏板,测得秋千摆动到右侧时与竖直方向的夹角∠AOD为34°,求秋千踏板在B、D处的高度差.(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675.结果精确到0.01)
苏科版九年级下 第7章 锐角三角函数 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、A 4、D 5、C 6、B 7、A 8、A 9、B 10、D 11、A 12、C
二.填空题(共5小题)
13、; 14、; 15、105°; 16、2; 17、;
三.解答题(共5小题)
18、解:(1)原式=()2+×
=+
=2;
(2)原式=2×--×1
=--
=-1.
19、解:(1)∵∠BDC=45°,∠C=90°,
∴∠CBD=∠BDC=45°,
∴BC=DC,
∵CD=25米,
∴BC=25米,
答:建筑物的高度为25米;
(2)设DC=BC=x米,
则,
∴x=20,
答:建筑物BC的高度为20米.
20、解:(1)连接AC,
技术人员测量的是A,C两点之间的距离,
理由测量的是A,C两点之间的距离,
理由如下:∵AC2+BC2=92+122=225,AC2=152=225,
∴AB2+BC2=AC2;,
∴∠ABC=90°;
(2)∵AD2+AC2=82+152=289,DC2=172=289,
∴AD2+AC2=DC2,
∴∠DAC=90°,
∴,
,
∴.
∴绿化这片空地共需花费100×114=11400元.
21、解:(1)过点D作DH⊥AC于点H,
∵AB⊥BG,
∴∠ABG=90°,
∵∠A=46°,
∴∠ACB=180°-90°-∠A=44°,
∵∠DCG=95°,
∴∠DCE=180°-∠ACB-∠DCG=41°,
∴在Rt△HDC中,HD=DC sin∠DCE=60 sin41°≈39.36(cm),
∴点D到AC的距离约为39.36cm;
(2)如图,过点E作EN⊥BG于点N,过点E'作E′M⊥BG于点M,
∵DE=DC,DH⊥AC,
∴在Rt△ENC中,EC=2HC=2×60 cos41°≈90.60(cm),
∴NE=CE sin44°=90.60 sin44°≈62.967(cm),
由题意得:CE'=2DE=120(cm),
∴在Rt△E′MC中,E′M=CE′ sin44°=120 sin44°≈83.40(cm),
83.40-62.967≈20.433≈20.43(cm),
∴点E上升的竖直高度约为20.43cm.
22、解:(1)如图,过点B作BE⊥OA,
由条件可知四边形BENM是矩形,
∴EN=1.2m,BE=MN=1.5m,
∵AN=0.7m,
∴AE=0.5m,
设秋千链子OA的长度为x m,
则OB=OA=x m,OE=OA-AE=(x-0.5)m,
在Rt△ABE中,(x-0.5)2+1.52=x2,
解得:x=2.5,
即秋千链子OA的长度为2.5m,
(2)如图,过点D作DF⊥OA于点F,
由(1)可知,OD=OA=2.5m,
在Rt△AFD中,∠AOD=34°,
∴OF=OD cos34°≈2.0725m,
∴点D离地面高度为1.1275m,
∴秋千踏板在B、D处的高度差为1.2-1.1275=0.0725≈0.07m.
一.选择题(共12小题)
1.如图,在△ABC中,∠C=90°,AB=5,AC=4,则cosA的值是( )
A. B. C. D.
2.如图,在△ABC中,∠A=90°,AB=4,BC=5,则cosB等于( )
A. B. C. D.
3.如图,市政府准备修建一座高AB=5米的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为,则坡面AC的长度为( )
A. B. C. D.
4.在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,下列各式成立的是( )
A.sinB= B.cosB= C.tanB= D.tanB=
5.某兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为45°,沿同一坡面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底D处,斜面AB的坡度(或坡比)i=1:2.4,则大树CD的高度为( )
A.5米 B.12米 C.13米 D.18米
6.如图,滨海办公区东、西两栋办公楼的高度相等,且水平距离为30m.下午3时太阳光线与地面所成的角是35°.这时东楼二层离地3m的阳台与西楼的楼顶、太阳恰好在一条直线上,则这两栋办公楼的高度为( )
A.(30 tan35°)m B.(30 tan35°+3)m
C.(30 cos35°+3)m D.
7.如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
8.一个木块静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行,若斜面的坡角α=30°13',则摩擦力F2与重力G的夹角β的度数为( )
A.120°13' B.149°47' C.130°13' D.159°47'
9.港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
10.图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40cm,α=37°,则双翼边缘端点C与D之间的距离为( )cm
A.60-40sin37° B.60-2×40cos37°
C.60-2×40tan37° D.60-2×40sin37°
11.在△ABC中,AB=BC,DA⊥AB交CB延长线于点D,DE⊥CA,垂足为E.若tan∠C=k,CD=1,则AD的值为( )
A.k B. C.k2 D.
12.某网红地惊现震撼的裸眼3D超清LED巨幕,成功吸引了广大游客前来打卡.小丽想了解该LED屏AB的高度,进行了实地测量,她从大楼底部C点沿水平直线步行30米到达台阶底端D点,在D点测得屏幕下端点B的仰角为27°,然后她再沿着i=4:3长度为35米的自动扶梯到达扶梯顶端E点,又沿水平直线行走了45米到达F点,在F点测得屏幕上端点A的仰角为50°(A,B,C,D,E,F,G在同一个平面内,且E、F和C、D、G分别在同一水平线上),则该LED屏AB的高度约为( )(结果精确到0.1,参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin50°≈0.77,tan50°≈1.19)
A.86.2米 B.114.2米 C.126.9米 D.142.2米
二.填空题(共5小题)
13.在Rt△ABC中,∠C=90°,BC:AC=3:4.则tanA=______.
14.如图,网格内每个小正方形的边长都是1个单位长度,A,B,C,D都是格点,且AB与CD相交于点P,则sin∠APD的值为 ______.
15.在△ABC中,若,则∠C=______.
16.如图,△ABC中,∠ACB=90°,BO为△ABC的角平分线,以点O为圆心,OC为半径作⊙O与边AC交于点D,若tanA=,AD=2,则tan∠BOC=______.
17.直角三角形ADE和ABC的直角顶点重合在点A,∠E=45°,∠C=60°,DE=AB=2,M、N分别是边AC、DE上的动点,且DN=AM,则AN+BM的最小值是 ______.
三.解答题(共5小题)
18.计算:
(1)sin245°+tan60° cos30°;
(2)2sin60°-cos60°-sin30° tan45°.
19.测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°(参考数据:sin50°=0.8,tan50°=1.2).
(1)若已知CD=25米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=4米,求建筑物BC的高度.
20.2020年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的四边形空地.如图,已知AB=9m,BC=12m,CD=17m,AD=8m,技术人员在只有卷尺的情况下,通过测量某两点之间距离为15m,便快速确定了∠ABC=90°.
(1)请写出技术人员测量的是哪两点之间的距离,并说明他确定∠ABC=90°的理由;
(2)若平均每平方米空地的绿化费用为100元,试计算绿化这片空地共需花费多少元?
21.2025年是“健康体重管理年”,某健身俱乐部精准把握时代脉搏购进健身器械,如图(1)所示的健身器械为倒蹬机,使用方法为上身不动,腿部向前发力,双腿伸直之后再慢慢收回.图(2)为其抽象示意图,已知DE,DC在初始位置,DE=DC=60cm,点B,C,G,在同一直线上,AB⊥BG,∠A=46°,∠DCG=95°.
(1)当DE,DC在初始位置时,求点D到AC的距离;
(2)当双腿伸直后,点E,D分别从初始位置运动到点E′,D′,假设E′,D′,C三点共线,求此时点E上升的竖直高度.(结果精确到0.01cm,参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869,sin44°≈0.695,cos44°≈0.719,tan44°≈0.966)
22.综合与实践
【教材重现】北师大版九年级下册教科书第9页例2:如图1,一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01).图2是该情境建模后的图形.(本题不用解答)
实际上,当秋千向两边摆动时,由于受摩擦力等其他因素的影响,两边摆动的角度一定不相同.某兴趣小组去到公园进行实地探究,测量了若干数据.请解答下列问题:
(1)如图3,秋千没摆动时,秋千的踏板离地面是0.7m,将它往左拉1.5m,此时踏板离地面1.2m,求秋千链子OA的长度;
(2)如图4,在(1)的条件下,释放踏板,测得秋千摆动到右侧时与竖直方向的夹角∠AOD为34°,求秋千踏板在B、D处的高度差.(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675.结果精确到0.01)
苏科版九年级下 第7章 锐角三角函数 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、A 4、D 5、C 6、B 7、A 8、A 9、B 10、D 11、A 12、C
二.填空题(共5小题)
13、; 14、; 15、105°; 16、2; 17、;
三.解答题(共5小题)
18、解:(1)原式=()2+×
=+
=2;
(2)原式=2×--×1
=--
=-1.
19、解:(1)∵∠BDC=45°,∠C=90°,
∴∠CBD=∠BDC=45°,
∴BC=DC,
∵CD=25米,
∴BC=25米,
答:建筑物的高度为25米;
(2)设DC=BC=x米,
则,
∴x=20,
答:建筑物BC的高度为20米.
20、解:(1)连接AC,
技术人员测量的是A,C两点之间的距离,
理由测量的是A,C两点之间的距离,
理由如下:∵AC2+BC2=92+122=225,AC2=152=225,
∴AB2+BC2=AC2;,
∴∠ABC=90°;
(2)∵AD2+AC2=82+152=289,DC2=172=289,
∴AD2+AC2=DC2,
∴∠DAC=90°,
∴,
,
∴.
∴绿化这片空地共需花费100×114=11400元.
21、解:(1)过点D作DH⊥AC于点H,
∵AB⊥BG,
∴∠ABG=90°,
∵∠A=46°,
∴∠ACB=180°-90°-∠A=44°,
∵∠DCG=95°,
∴∠DCE=180°-∠ACB-∠DCG=41°,
∴在Rt△HDC中,HD=DC sin∠DCE=60 sin41°≈39.36(cm),
∴点D到AC的距离约为39.36cm;
(2)如图,过点E作EN⊥BG于点N,过点E'作E′M⊥BG于点M,
∵DE=DC,DH⊥AC,
∴在Rt△ENC中,EC=2HC=2×60 cos41°≈90.60(cm),
∴NE=CE sin44°=90.60 sin44°≈62.967(cm),
由题意得:CE'=2DE=120(cm),
∴在Rt△E′MC中,E′M=CE′ sin44°=120 sin44°≈83.40(cm),
83.40-62.967≈20.433≈20.43(cm),
∴点E上升的竖直高度约为20.43cm.
22、解:(1)如图,过点B作BE⊥OA,
由条件可知四边形BENM是矩形,
∴EN=1.2m,BE=MN=1.5m,
∵AN=0.7m,
∴AE=0.5m,
设秋千链子OA的长度为x m,
则OB=OA=x m,OE=OA-AE=(x-0.5)m,
在Rt△ABE中,(x-0.5)2+1.52=x2,
解得:x=2.5,
即秋千链子OA的长度为2.5m,
(2)如图,过点D作DF⊥OA于点F,
由(1)可知,OD=OA=2.5m,
在Rt△AFD中,∠AOD=34°,
∴OF=OD cos34°≈2.0725m,
∴点D离地面高度为1.1275m,
∴秋千踏板在B、D处的高度差为1.2-1.1275=0.0725≈0.07m.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
