苏科版数学教材九年级下册 第6章 图形的相似 单元测试(含答案)
文档属性
| 名称 | 苏科版数学教材九年级下册 第6章 图形的相似 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 125.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 23:35:09 | ||
图片预览




文档简介
苏科版九年级下 第6章 图形的相似 单元测试
一.选择题(共12小题)
1.若两个相似三角形的周长比为1:3,则它们的面积比为( )
A.1:2 B.1:3 C.1:6 D.1:9
2.如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD:DB=3:2,则AE:AC等于( )
A.3:2 B.3:1 C.2:3 D.3:5
3.如图,△ABC与△DEF是以点O为位似中心的位似图形,若△ABC与△DEF的面积比为4:9,则OA:OD为( )
A.4:9 B.2:3 C.2:1 D.3:1
4.大自然是美的设计师,即使是一片小小的树叶也蕴含着“美学”.如图,枫叶的叶柄BP和主叶脉AP的比值接近黄金比.估计的值应在( )
A.0到0.5之间 B.0.5到1之间 C.1到1.5之间 D.1.5到2之间
5.如果2m=3n(n≠0),那么下列比例式中正确的是( )
A. B. C. D.
6.如图,已知AB∥CD∥EF,若AC=6,CE=3,DF=2,则BD的长为( )
A.4 B.4.5 C.5.5 D.6
7.某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,则河的宽度PQ是( )
A.70m B.80m C.90m D.100m
8.(2025 滑县校级三模)如图,已知 ABCD,E是AD的中点,连接BE,AC相交于点F,FG∥AD,若BC=6,则FG的长是( )
A.1 B.1.5 C.2 D.2.5
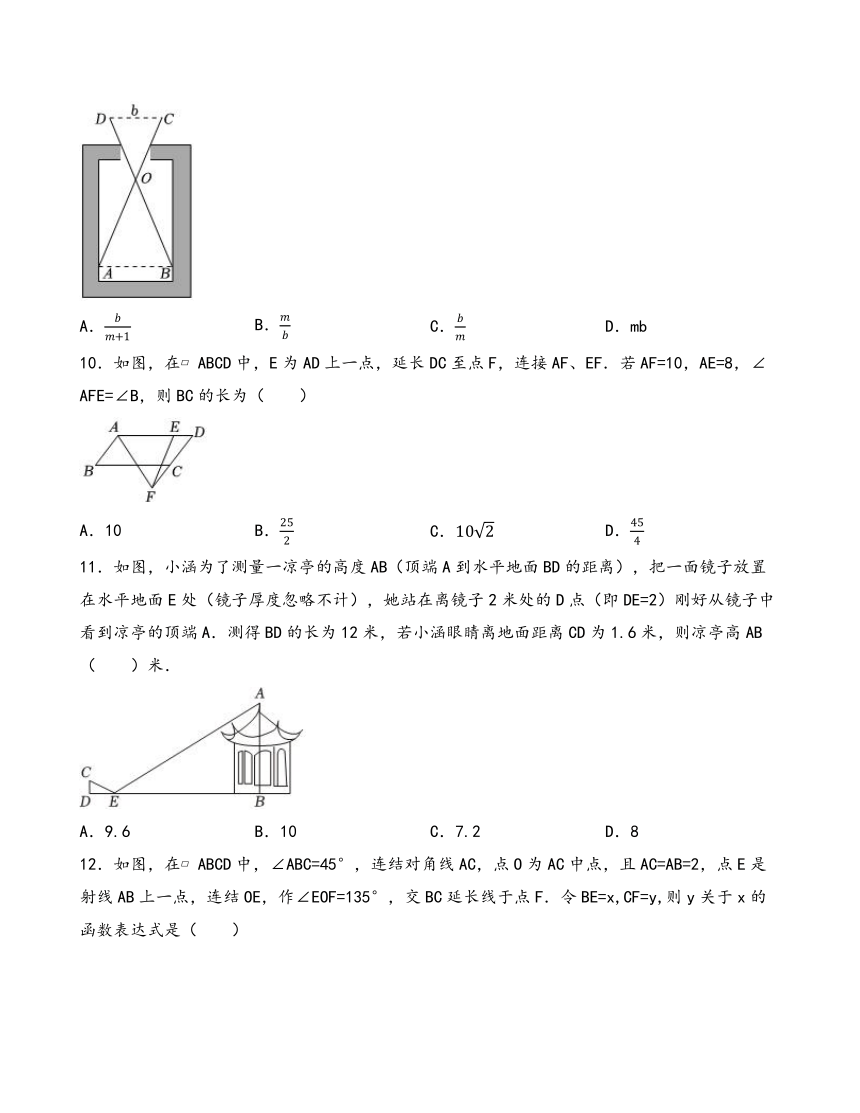
9.如图,用一个交叉卡钳(两条尺长AC和BD相等)测量零件的内孔直径AB.如果OA:OC=OB:OD=m,且量得CD=b,则AB等于( )
A. B. C. D.mb
10.如图,在 ABCD中,E为AD上一点,延长DC至点F,连接AF、EF.若AF=10,AE=8,∠AFE=∠B,则BC的长为( )
A.10 B. C. D.
11.如图,小涵为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),把一面镜子放置在水平地面E处(镜子厚度忽略不计),她站在离镜子2米处的D点(即DE=2)刚好从镜子中看到凉亭的顶端A.测得BD的长为12米,若小涵眼睛离地面距离CD为1.6米,则凉亭高AB( )米.
A.9.6 B.10 C.7.2 D.8
12.如图,在 ABCD中,∠ABC=45°,连结对角线AC,点O为AC中点,且AC=AB=2,点E是射线AB上一点,连结OE,作∠EOF=135°,交BC延长线于点F.令BE=x,CF=y,则y关于x的函数表达式是( )
A. B. C. D.
二.填空题(共5小题)
13.若a:b:c=1:2:3,则=______.
14.大自然是美的设计师,即使是一个小小的盆景,经常也会产生最具美感的黄金分割比例.如图,点B为AC的黄金分割点,即AB2=BC AC.若AC=20cm,则BC的长为 ______cm.
15.如图,正五角星中包含了许多黄金三角形,许多线段之间构成了黄金比,如点C是线段AD的黄金分割点(AC>CD)则有,已知厘米,那么AC= ______厘米.
16.如图,在四边形ABCD中,∠C=90°,,AD=CD=10,点E、F分别在边AD、BC上,连接EF,点G为EF的中点,连接AG,若AE=6,则点AG的最小长度为 ______.
17.如图,在正方形ABCD中,点E,点F分别在边BC,AB上(点E不与点B,C重合),且AF=BE.连接AC,DF交于点G,连接AE,BG交于点H.若DF=4GH,则= ______.
三.解答题(共5小题)
18.如图,在△ABC中,D是AB上一点,连接CD,已知AC2=AD AB.
(1)求证:△ACD∽△ABC;
(2)若∠A=32°,∠BDC=75°,求∠DCB的度数.
19.如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),点D,F分别在边AB和AC上,且满足∠DEF=∠B.
(1)求证:△BDE∽△CEF;
(2)若BE=CE,且BD=3,CF=2,求的值.
20.如图,AB是⊙O的直径,D是⊙O上一点,连接AD和BD,C是的中点,连接OC和AC,分别交BD于点E和F.
(1)证明:AD∥OC;
(2)若BO=5,BE=4,求DF的长.
21.如图,在△ABC中,BD平分∠ABC交AC于点D,点E在边BC上,满足∠BAE=∠ACB.连接AE交BD于点F,过点F作FG∥BC交CD于点G.
(1)求证:AF=AD;
(2)求证:△DFG∽△FBA;
(3)若BE=2EF,求的值.
22.问题情境 借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.如图1,在△ABC中,∠B=90°,AB=BC=4,分别取AB、AC的中点D、E,作△ADE.如图2所示,将△ADE绕点A逆时针旋转,连接BD、CE.
【探究发现】旋转过程中,线段BD和CE存在怎样的数量关系?写出你的猜想,并加以证明.
【类比应用】如图3,当DE所在直线首次经过点B时,求CE的长.
【延伸思考】如图4,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别取AB、BC的中点D、E.作△BDE,将△BDE绕点B逆时针旋转,连接AD、CE.当BD首次与AC平行时,求△ECB的面积.
苏科版九年级下 第6章 图形的相似 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、D 3、B 4、B 5、A 6、A 7、C 8、C 9、D 10、B 11、D 12、B
二.填空题(共5小题)
13、5; 14、; 15、2; 16、9; 17、;
三.解答题(共5小题)
18、(1)证明:∵AC2=AD AB,
∴=,
∵∠A=∠A,
∴△ACD∽△ABC.
(2)解:∵∠A=32°,∠BDC=75°,
∴∠ACD=∠BDC-∠A=75°-32°=43°,
∵△ACD∽△ABC,
∴∠ACD=∠B=43°,
∴∠DCB=180°-∠BDC-∠B=180°-75°-43°=62°,
∴∠DCB的度数是62°.
19、(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠DEC=∠B+∠BDE=∠DEF+∠CEF,∠DEF=∠B,
∴∠BDE=∠CEF,
∴△BDE∽△CEF;
(2)解:∵△BDE∽△CEF,
∴=,
∵BE=CE,BD=3,CF=2,
∴BE=CE=,
∴==.
20、(1)证明:∵AB是⊙O的直径,
∴∠D=90°,
∵C是的中点,
∴OC垂直平分BD,
∴∠OEB=90°,
∴∠D=∠OEB,
∴AD∥OC.
(2)解:∵AO=BO=CO=5,DE=BE=4,
∴AB=2AO=10,DB=2DE=8,
∴AD===6,
∴OE=AD=3,
∴CE=CO-OE=5-3=2,
∵AD∥CE,
∴△AFD∽△CFE,
∴===3,
∴EF=DF,
∴DF+DF=4,
∴DF=3,
∴DF的长为3.
21、(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵FG∥BC,
∴∠FGA=∠ACB,
∵∠BAE=∠ACB,
∴∠BAE=∠ACB=∠FGA,
∵∠AFD=∠BAE+∠ABD,∠ADB=∠CBD+∠ACB,
∴∠AFD=∠ADB,
∴AF=AD;
(2)证明:∵FG∥BC,
∴∠CBD=∠DFG,
∴∠ABD=∠DFG,∠BAE=∠FGD,
∴△DFG∽△FBA;
(3)∵∠BFE=∠AFD=∠ADF,∠ABD=∠EBD,
∴△BEF∽△BAD,
∴,
又由(1)可得AD=AF,
∴.
由(2)知△DFG∽△FBA,
故=.
22、解:【探究发现】,理由如下:
∵点D和点E为分别为AB,AC中点,
∴,,
∴,
∴,
∵∠B=90°,AB=BC=4,
∴∠BAC=45°,
∴,
根据旋转的性质可得:∠BAD=∠CAE,
∴△ABD∽△ACE,
∴,即;
【类比应用】由图1可知,
∵点D和点E为分别为AB,AC中点,
∴DE∥BC,AB=2,
∴△ABC∽△ADE,
∴∠ADE=∠ABC=90°,
∴当DE所在直线经过点B时,AD⊥BE,
根据勾股定理可得:,
由【探究发现】可得:,
∴,
解得:;
【延伸思考】过点E作EG⊥BC于点G,
根据题意可得:,
∵∠ABC=90°,AB=8,BC=6,
∴,
∴,
∵AC∥BD,
∴∠BAC=∠ABD,
根据旋转的性质可得:∠ABD=∠EBC,
∴∠CAB=∠EBC,
∴,
∴,
∴.
一.选择题(共12小题)
1.若两个相似三角形的周长比为1:3,则它们的面积比为( )
A.1:2 B.1:3 C.1:6 D.1:9
2.如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD:DB=3:2,则AE:AC等于( )
A.3:2 B.3:1 C.2:3 D.3:5
3.如图,△ABC与△DEF是以点O为位似中心的位似图形,若△ABC与△DEF的面积比为4:9,则OA:OD为( )
A.4:9 B.2:3 C.2:1 D.3:1
4.大自然是美的设计师,即使是一片小小的树叶也蕴含着“美学”.如图,枫叶的叶柄BP和主叶脉AP的比值接近黄金比.估计的值应在( )
A.0到0.5之间 B.0.5到1之间 C.1到1.5之间 D.1.5到2之间
5.如果2m=3n(n≠0),那么下列比例式中正确的是( )
A. B. C. D.
6.如图,已知AB∥CD∥EF,若AC=6,CE=3,DF=2,则BD的长为( )
A.4 B.4.5 C.5.5 D.6
7.某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,则河的宽度PQ是( )
A.70m B.80m C.90m D.100m
8.(2025 滑县校级三模)如图,已知 ABCD,E是AD的中点,连接BE,AC相交于点F,FG∥AD,若BC=6,则FG的长是( )
A.1 B.1.5 C.2 D.2.5
9.如图,用一个交叉卡钳(两条尺长AC和BD相等)测量零件的内孔直径AB.如果OA:OC=OB:OD=m,且量得CD=b,则AB等于( )
A. B. C. D.mb
10.如图,在 ABCD中,E为AD上一点,延长DC至点F,连接AF、EF.若AF=10,AE=8,∠AFE=∠B,则BC的长为( )
A.10 B. C. D.
11.如图,小涵为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),把一面镜子放置在水平地面E处(镜子厚度忽略不计),她站在离镜子2米处的D点(即DE=2)刚好从镜子中看到凉亭的顶端A.测得BD的长为12米,若小涵眼睛离地面距离CD为1.6米,则凉亭高AB( )米.
A.9.6 B.10 C.7.2 D.8
12.如图,在 ABCD中,∠ABC=45°,连结对角线AC,点O为AC中点,且AC=AB=2,点E是射线AB上一点,连结OE,作∠EOF=135°,交BC延长线于点F.令BE=x,CF=y,则y关于x的函数表达式是( )
A. B. C. D.
二.填空题(共5小题)
13.若a:b:c=1:2:3,则=______.
14.大自然是美的设计师,即使是一个小小的盆景,经常也会产生最具美感的黄金分割比例.如图,点B为AC的黄金分割点,即AB2=BC AC.若AC=20cm,则BC的长为 ______cm.
15.如图,正五角星中包含了许多黄金三角形,许多线段之间构成了黄金比,如点C是线段AD的黄金分割点(AC>CD)则有,已知厘米,那么AC= ______厘米.
16.如图,在四边形ABCD中,∠C=90°,,AD=CD=10,点E、F分别在边AD、BC上,连接EF,点G为EF的中点,连接AG,若AE=6,则点AG的最小长度为 ______.
17.如图,在正方形ABCD中,点E,点F分别在边BC,AB上(点E不与点B,C重合),且AF=BE.连接AC,DF交于点G,连接AE,BG交于点H.若DF=4GH,则= ______.
三.解答题(共5小题)
18.如图,在△ABC中,D是AB上一点,连接CD,已知AC2=AD AB.
(1)求证:△ACD∽△ABC;
(2)若∠A=32°,∠BDC=75°,求∠DCB的度数.
19.如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),点D,F分别在边AB和AC上,且满足∠DEF=∠B.
(1)求证:△BDE∽△CEF;
(2)若BE=CE,且BD=3,CF=2,求的值.
20.如图,AB是⊙O的直径,D是⊙O上一点,连接AD和BD,C是的中点,连接OC和AC,分别交BD于点E和F.
(1)证明:AD∥OC;
(2)若BO=5,BE=4,求DF的长.
21.如图,在△ABC中,BD平分∠ABC交AC于点D,点E在边BC上,满足∠BAE=∠ACB.连接AE交BD于点F,过点F作FG∥BC交CD于点G.
(1)求证:AF=AD;
(2)求证:△DFG∽△FBA;
(3)若BE=2EF,求的值.
22.问题情境 借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.如图1,在△ABC中,∠B=90°,AB=BC=4,分别取AB、AC的中点D、E,作△ADE.如图2所示,将△ADE绕点A逆时针旋转,连接BD、CE.
【探究发现】旋转过程中,线段BD和CE存在怎样的数量关系?写出你的猜想,并加以证明.
【类比应用】如图3,当DE所在直线首次经过点B时,求CE的长.
【延伸思考】如图4,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别取AB、BC的中点D、E.作△BDE,将△BDE绕点B逆时针旋转,连接AD、CE.当BD首次与AC平行时,求△ECB的面积.
苏科版九年级下 第6章 图形的相似 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、D 3、B 4、B 5、A 6、A 7、C 8、C 9、D 10、B 11、D 12、B
二.填空题(共5小题)
13、5; 14、; 15、2; 16、9; 17、;
三.解答题(共5小题)
18、(1)证明:∵AC2=AD AB,
∴=,
∵∠A=∠A,
∴△ACD∽△ABC.
(2)解:∵∠A=32°,∠BDC=75°,
∴∠ACD=∠BDC-∠A=75°-32°=43°,
∵△ACD∽△ABC,
∴∠ACD=∠B=43°,
∴∠DCB=180°-∠BDC-∠B=180°-75°-43°=62°,
∴∠DCB的度数是62°.
19、(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠DEC=∠B+∠BDE=∠DEF+∠CEF,∠DEF=∠B,
∴∠BDE=∠CEF,
∴△BDE∽△CEF;
(2)解:∵△BDE∽△CEF,
∴=,
∵BE=CE,BD=3,CF=2,
∴BE=CE=,
∴==.
20、(1)证明:∵AB是⊙O的直径,
∴∠D=90°,
∵C是的中点,
∴OC垂直平分BD,
∴∠OEB=90°,
∴∠D=∠OEB,
∴AD∥OC.
(2)解:∵AO=BO=CO=5,DE=BE=4,
∴AB=2AO=10,DB=2DE=8,
∴AD===6,
∴OE=AD=3,
∴CE=CO-OE=5-3=2,
∵AD∥CE,
∴△AFD∽△CFE,
∴===3,
∴EF=DF,
∴DF+DF=4,
∴DF=3,
∴DF的长为3.
21、(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵FG∥BC,
∴∠FGA=∠ACB,
∵∠BAE=∠ACB,
∴∠BAE=∠ACB=∠FGA,
∵∠AFD=∠BAE+∠ABD,∠ADB=∠CBD+∠ACB,
∴∠AFD=∠ADB,
∴AF=AD;
(2)证明:∵FG∥BC,
∴∠CBD=∠DFG,
∴∠ABD=∠DFG,∠BAE=∠FGD,
∴△DFG∽△FBA;
(3)∵∠BFE=∠AFD=∠ADF,∠ABD=∠EBD,
∴△BEF∽△BAD,
∴,
又由(1)可得AD=AF,
∴.
由(2)知△DFG∽△FBA,
故=.
22、解:【探究发现】,理由如下:
∵点D和点E为分别为AB,AC中点,
∴,,
∴,
∴,
∵∠B=90°,AB=BC=4,
∴∠BAC=45°,
∴,
根据旋转的性质可得:∠BAD=∠CAE,
∴△ABD∽△ACE,
∴,即;
【类比应用】由图1可知,
∵点D和点E为分别为AB,AC中点,
∴DE∥BC,AB=2,
∴△ABC∽△ADE,
∴∠ADE=∠ABC=90°,
∴当DE所在直线经过点B时,AD⊥BE,
根据勾股定理可得:,
由【探究发现】可得:,
∴,
解得:;
【延伸思考】过点E作EG⊥BC于点G,
根据题意可得:,
∵∠ABC=90°,AB=8,BC=6,
∴,
∴,
∵AC∥BD,
∴∠BAC=∠ABD,
根据旋转的性质可得:∠ABD=∠EBC,
∴∠CAB=∠EBC,
∴,
∴,
∴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
