(小升初择校分班考)小升初重点中学分班考押题卷-2024-2025学年六年级下册数学北京版(含解析)
文档属性
| 名称 | (小升初择校分班考)小升初重点中学分班考押题卷-2024-2025学年六年级下册数学北京版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 286.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 15:20:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点中学分班考押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.下列四个选项中,正确的是( )。
A.一个不透明的盒子里装了红、黑、白玻璃球各4个,要保证取出的玻璃球3种颜色都有,至少要取9个玻璃球。
B.如果y=5x(x、y≠0),那么x和y成反比例。
C.1枚硬币掷3次有2次正面朝上,1次反面朝上,那么掷第4次一定正面朝上。
D.等腰三角形的两边长分别为4厘米和2厘米,则这个三角形的周长是8厘米或10厘米。
2.把m+1个物体放进m个抽屉里,总有一个抽屉里至少放进( )个物体(m为大于0的自然数)。
A.m B. C.2 D.1
3.一条毛毛虫从幼虫长到成虫,每天长大一倍,22天能长到20厘米,当长到5厘米时,需要用( )天。
A.21 B.20 C.19 D.18
4.小明和小华用黑桃2-9做游戏,任意摸一张牌,不公平的是( )。
A.摸到奇数小明赢,摸到偶数小华赢。 B.摸到质数小明赢,摸到合数小华赢。
C.摸到大于5的小明赢,摸到小于5的小华赢。 D.摸到3或5的倍数小明赢,否则小华赢。
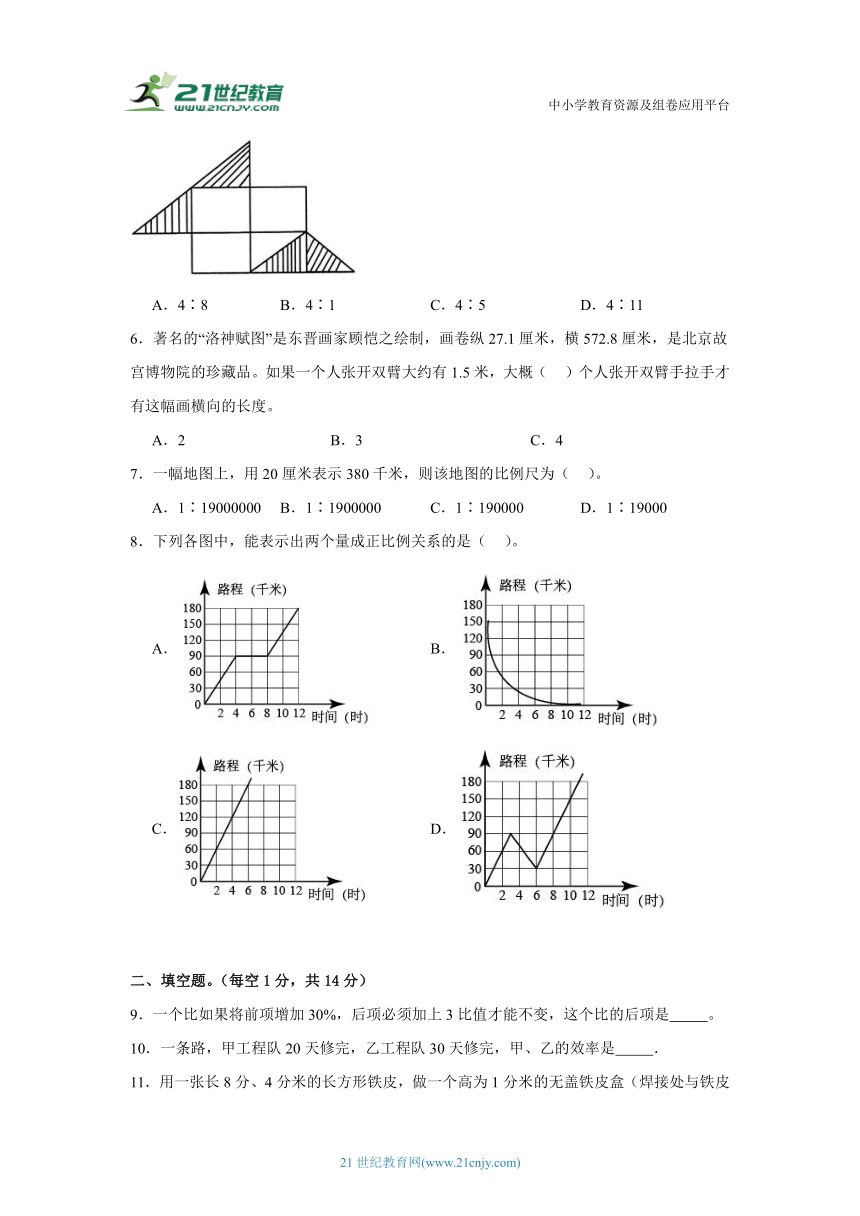
5.图示为一幅图形的密铺方案,则此阴影部分的面积和整个图形的面积比为( )。
A.4∶8 B.4∶1 C.4∶5 D.4∶11
6.著名的“洛神赋图”是东晋画家顾恺之绘制,画卷纵27.1厘米,横572.8厘米,是北京故宫博物院的珍藏品。如果一个人张开双臂大约有1.5米,大概( )个人张开双臂手拉手才有这幅画横向的长度。
A.2 B.3 C.4
7.一幅地图上,用20厘米表示380千米,则该地图的比例尺为( )。
A.1∶19000000 B.1∶1900000 C.1∶190000 D.1∶19000
8.下列各图中,能表示出两个量成正比例关系的是( )。
A. B.
C. D.
二、填空题。(每空1分,共14分)
9.一个比如果将前项增加30%,后项必须加上3比值才能不变,这个比的后项是 。
10.一条路,甲工程队20天修完,乙工程队30天修完,甲、乙的效率是 .
11.用一张长8分、4分米的长方形铁皮,做一个高为1分米的无盖铁皮盒(焊接处与铁皮厚不计),这个铁皮盒最大的容积 立方分米.
12.甲、乙、丙三名滑冰运动员在一起训练。已知,甲滑1圈时,乙能滑圈,丙能滑圈。三人同时同地出发,甲滑 圈时,三个人第一次再相遇。
13.甲、乙两城市的距离是120千米,甲、乙两城之间有一个电视塔,电视塔距甲、乙两城的距离比为1∶5,乙城和电视塔之间的距离为 千米。
14.如图,一根长2米的圆柱形木料,截去一半后,剩下的圆柱形木料的表面积比原来减少了62.8平方分米,原来圆柱形木料的底面积是 平方分米,体积是 立方分米。
15.施灵为了测量萝卜的体积,先将一个萝卜削成一个长5厘米、宽4厘米、高2厘米的长方体,并用天平称出这个长方体重20克。接着用天平称出要测量体积的萝卜重320克。这个萝卜的体积是 立方厘米。
16.在美术中,让人觉得最美的比例叫黄金比例,它的比例是1∶0.618,要让重光宝塔的高和直径成黄金比例,如果高是20m,直径应是 m。
17.图中的大圆半径等于小圆的直径。大圆周长与小圆周长的比是 。
18.某车间人数不超过100人,已知男工人数的等于女工人数的,这个车间男工与女工最多相差 人。
19.把一个高为3cm的圆柱的侧面展开得到一个长方形,这个长方形的长是12.56cm。这个圆柱的表面积是 平方厘米,体积是 立方厘米。
20.配制一种药水,在1.8千克的水中,放入200克药剂那么药剂的质量与药水总质量的比是 .
三、判断题。(每题1分,共5分)
21.收割机的台数和收割的总面积不成比例。( )
22.在比例中,两个内项分别是3和4,两个外项的和是12。( )
23.一种精密零件,长2毫米,画在一幅图上长10厘米,这幅图的比例尺是1∶50。( )
24.一个直角三角形的两条直角边都放大到原来的4倍后,面积也放大到原来的4倍。( )
25.梯形的面积一定时,上、下底之和与高成反比例。( )
四、计算题。(共33分)
26.直接写得数.(共8分)
4.8×= 598-392= 6.7+3= 1.25×0.8-1%=
5.1×= ×÷×= (3.6+7.2)÷0.9= 3.4×÷4=
27.计算下面各题.(能简算的要简算,共12分)
7.28一(1.28+0.25) 905×99+905 20×÷× 16.8÷[32×(1-)]
28.解方程或比例。(共9分)
29.计算下面图形的表面积。(共4分)
五、操作题。(共4分)
30.看图,先算出小梅家和小芳家的图上距离,再按要求在下图中标出两家的位置。
(1)小梅家在学校正南方向约300米处;
(2)小芳家在学校北偏西30°约400米处。
六、解答题。(每题6分,共36分)
31.某地为治理荒漠化,在沙漠上种植了一批沙柳树苗,1个月后树苗的死亡棵数与成活棵数的比是5∶11,如果成活了1760棵,那么这批沙柳树苗的总棵数是多少?
32.将底面积60平方厘米,高15厘米的圆柱形状水槽注满水,然后将水倒入底面积是100平方厘米,高是30厘米的圆锥形容器中。圆锥形容器能装下这些水吗?写出过程。(题目中数据都是从水槽、圆锥形容器内部测量得到的)
33.甲、乙两列火车同时从两站相对开出,相遇后又继续行驶了1.2小时,这时两车相距186千米,已知两列火车的速度比是16∶15,两车每小时各行驶多少千米?(用两种方法解)
34.如图,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和形区域乙和丙。已知三块区域甲、乙、丙的周长之比,并且区域丙的面积为48,求大正方形的面积。
35.已知三种混合物由三种成分A、B、C组成,第一种仅含成分A和B,重量比为3∶5;第二种只含成分B和C,重量比为1∶2;第三种只含成分A和C,重量之比为2∶3。以什么比例取这些混合物,才能使所得的混合物中A、B和C,这三种成分的重量比为3∶5∶2?
36.张亮在一个长方体的玻璃容器中装了一些水,他把一个底面半径为的圆柱形铁块完全浸入水中,发现水面上升了。他又把这个铁块垂直拉出水面,这时水面下降(如下图所示,玻璃厚度忽略不计)。
(1)这个铁块露出水面部分的体积是多少?(取3)
(2)这个铁块的体积是多少?(取3)
(3)这个铁块的体积占玻璃容器容积的百分之几?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】A.从最极端的情况分析,假设把红球和黑球都取完,就是取8个玻璃球,这时候,再取一个球,就可以保证取出的玻璃球3种颜色都有;
B.判断x和y之间是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例;
C.抛硬币只会出现正面朝上和反面朝上两种结果,每种结果朝上的可能性都为,不会受投掷的次数影响;
D.等腰三角形的两边长分别为4厘米和2厘米,有两种情况,腰长可能是4厘米,也可能是2厘米,当腰长是4厘米时,另一条边长是2厘米,三角形的周长是10厘米;当腰长是2厘米时,另一条边长是4厘米,周长是8厘米;但考虑三角形的三边长的关系,2+2=4,不符合三角形的三条边长的关系,所以当腰长是2厘米时不满足条件,腰长只能是4厘米。
【解析】A.4+4+1=9(个);至少要取9个玻璃球,能保证取出的玻璃球3种颜色都有。原题说法正确;
B.如果y=5x(x、y≠0),y÷x=5(一定),y和x的商一定,所以x和y成正比例,原题说法错误;
C.每次抛硬币是一个独立事件,下一次的结果不会受前一次的影响,所以可能出现1枚硬币掷3次有2次正面朝上,1次反面朝上这样的事件,但并能说明正面朝上的可能性比反面朝上的可能性大。所以原题说法错误;
D.根据分析得,腰长只能是4厘米,4+4+2=10(厘米),周长是10厘米;所以原题说法错误。
故答案为:A
【点评】此题的综合性较强,涉及各个章节的基础知识,注意平时知识的积累。
2.C
【分析】根据鸽巢原理:如果把(n+1)个物体放在n个抽屉里,那么必有一个抽屉里至少放有两个物体;据此解答即可。
【解析】由分析可得:把(m+1)个物体放进m个抽屉里,总有一个抽屉放进2个物体。
故答案为:C
【点评】本题主要考查了鸽巢原理的应用,关键是要理解巢原理。
3.B
【分析】采用倒推的方法,每天长大一倍,22天20厘米;到21天为20÷2=10厘米,20天为10÷5=5厘米,据此解答。
【解析】21天:20÷2=10(厘米)
20天:10÷2=5(厘米)
一条毛毛虫从幼虫长到成虫,每天长大一倍,22天能长到20厘米,当长到5厘米时,需要用20天。
故答案为:B
【点评】本题考查的知识点是用倒推法或者叫还原法来解答趣味数学问题,解答此题的关键条件是每天长大一倍。
4.C
【分析】在摸牌游戏中,只要双方发生的概率相等,游戏就公平,反之就不公平;据此解答。
【解析】A.2-9的数字中,奇数有3、5、7、9共4个,偶数有2、4、6、8共4个,奇数和偶数的个数相等,俩人摸到的概率相同;游戏公平;
B. 2-9的数字中,质数有2、3、5、7共4个,合数有4、6、8、9共4个,质数和合数的个数相同,俩人摸到的概率相同;游戏公平;
C. 2-9的数字中,大于5的数有6、7、8、9共4个,小于5的数有2、3、4共3个数,摸到大于5的概率比摸到小于5的概率大,游戏不公平;
D. 2-9的数字中,3或5的倍数有3、5、6、9,不是3或5的倍数有2、4、7、8,3或5的倍数与不是3或5的倍数的数的个数相同,俩人摸到的概率相同;游戏公平。
故答案为:C。
【点评】本题考查的是判断可能事件的概率的大小。
5.D
【分析】根据题图可知,整个图形可以分成11个完全相同的小三角形,阴影部分为4个小三角形,据此写出它们之间的比即可。
【解析】阴影部分的面积和整个图形的面积比为4∶11;
故答案为:D
【点评】解答本题的关键是将整个图形分成面积相等的小三角形,再进一步解答。
6.C
【分析】1米=100厘米,因此先用1.5乘100将1.5米化成厘米,然后计算出横572.8厘米的近似数,这个近似数里面大约有几个150厘米就大概有几个人张开双臂手拉手才有这幅画横向的长度。
【解析】1.5米=150厘米
572.8厘米≈573厘米;
150×4=600厘米;
573厘米≈600厘米;
因此大概4个人张开双臂手拉手才有这幅画横向的长度。
故答案为:C
【点评】此题考查的是米和厘米之间的换算、小数的近似数、整数的近似数,要熟练掌握。
7.B
【分析】比例尺=图上距离∶实际距离,据此解答。
【解析】380千米=38000000厘米
则该地图的比例尺为:20∶38000000=1∶1900000。
故选择:B
【点评】此题考查了比例尺的意义,换算单位时注意数清0的个数。
8.C
【分析】首先要知道成正比例关系的图象特点是一条经过原点的直线,相关联的两个量应是比值或商一定;据此即可作出正确选择。
【解析】A.不是一条直线,不符合题意;
B.是一条曲线,不是直线,不符合题意;
C.是一条经过原点的直线,符合题意;
D.不是一条直线,不符合题意。
故答案为:C。
【点评】本题主要考查正比例的图像,熟练掌握正比例的图像并灵活运用。
9.10
【分析】根据比的性质可知:如果比的前项增加30%,要使比值不变,那么后项也要增加30%,进而根据后项增加的30%是3,用3除以30%即得这个比的后项。
【解析】比的前项增加30%,要使比值不变,后项也要增加30%,那么3÷30%=10。
答:这个比的后项是10。
故答案为10。
【点评】解决此题关键是理解如果比的前项增加30%,要使比值不变,后项也要增加30%,进一步得解。
10.3:2.
【分析】把工作总量看作单位“1”,根据甲、乙两个工程队所用的时间,分别求出甲、乙两个工程队的工作效率,进而写出工作效率比并化简比.
【解析】甲的效率:1÷20=,
乙的效率,1,
甲、乙的效率比::=3:2;
11.12
【解析】试题分析:画图,结合图形找出长方体的长、宽、高,由体积计算公式解答即可.
解:如图,
铁皮盒的容积:
1×( 8﹣1×2)×( 4﹣1×2 ),
=1×6×2,
="12" (dm3);
答:这个铁皮盒的容积最大是12立方分米;
故答案为12.
点评:此题主要考查长方体的体积计算公式:长方体的体积=长×宽×高.
12.12
【分析】由题可得,3人的滑冰速度比为:1∶∶,化成最简整数比为:12∶16∶15。三人同时同地出发,当三人相遇时,一定是三人刚好同时回到出发点,即三人刚好同时滑了整圈数,此时甲滑了12圈。
【解析】1∶∶=12∶16∶15,当甲滑12圈时,三个人第一次再相遇。
【点评】本题考查最简整数比的应用,理解三个人何时第一次再相遇时解答此题的关键。
13.100
【分析】因为甲、乙两城之间的距离是120千米,它们之间有一个电视塔,而且电视塔距甲、乙两城的距离比为1∶5,就相当于把120千米平均分成6份,而乙城和电视塔之间的距离是6份中的5份。
【解析】120÷(1+5)×5
=120÷6×5
=20×5
=100(千米)
【点评】本题主要考查按比分配,解题关键是把总距离平均分成6份,乙城和电视塔之间的距离是其中5份。
14.3.14 62.8
【分析】减少的表面积就是截去一半圆柱的侧面积,根据底面周长=侧面积÷高,底面面积=(底面周长÷π÷2)2×π,体积=底面积×高,代入数据计算即可。
【解析】2÷2=1(米)
1米=10分米
62.8÷10÷3.14÷2
=6.28÷3.14÷2
=1(分米)
3.14×12=3.14(平方分米)
2米=20分米
3.14×20=62.8(立方分米)
【点评】这是一道关于圆柱的题目,根据圆柱的侧面积和体积公式、圆的周长和面积公式解答。
15.640
【分析】先求出长方体体积,再算出每立方厘米的重量,用总重量÷每立方厘米重量=总体积。
【解析】320÷[20÷(5×4×2)]
=320÷[20÷40]
=320÷0.5
=640(立方厘米)
【点评】本题考查了不规则物体体积的算法,通过重量求出体积,方法比较巧妙。
16.12.36
【分析】根据“它的比例是1∶0.618”,即重光宝塔的高和直径的比值是一定的,由此列出比例,解决问题。
【解析】解:设直径应是xm,
1∶0.618=20∶x
x=0.618×20
x=12.36
答:直径应是12.36m。
故答案为:12.36。
【点评】本题主要考查了比例的应用,解答此题的关键是判断出重光宝塔的高和直径成正比例。
17.2∶1
【分析】设小圆的半径是r,则小圆的直径是2r,大圆的半径是2r,根据“圆的周长=2πr”分别计算出大圆和小圆的周长,然后进行比即可。
【解析】设小圆的半径是r,则小圆的直径是2r,大圆的半径是2r,则:
[2×π×(2r)]∶(2πr)
=4πr∶2πr
=2∶1
【点评】解答此题应根据圆的周长的计算方法进行解答即可。
18.45
【分析】男工人数的等于女工人数的,所以男工人数∶女工人数=∶=8∶3,男工人数和女工人数的总份数是8+3=11,因为某车间人数不超过100人,100以内11的倍数最大是99,所以这个车间男工与女工最多相差的人数=99÷总份数×(男工人数占的人数-女工人数占的人数)。
【解析】男工人数∶女工人数=∶=8∶3
8+3=11,100以内11的倍数最大是99,99÷11×(8-3)=45,所以这个车间男工与女工最多相差45人。
19.62.8 37.68
【分析】(1)圆柱的表面积=侧面积+底面积×2;圆柱的侧面积=底面周长×高;本题圆柱侧面展开是一个长方形,长方形的长就是圆柱的底面周长。先用底面周长求出圆柱的底面半径,然后求出底面积,再求出圆柱侧面积,最后求出圆柱的表面积。
(2)圆柱的体积=底面积×高,先用底面周长求出圆柱的底面半径,然后用体积公式求出圆柱的体积。
【解析】(1)12.56÷3.14÷2=2(厘米)
3.14×2 ×2=25.12(平方厘米)
12.56×3=37.68(平方厘米)
25.12+37.68=62.8(平方厘米)
(2)12.56÷3.14÷2=2(厘米)
3.14×2 ×3=37.68(立方厘米)
20.1∶10
【解析】略
21.√
【分析】两个相关联的量,一个量变化另一个量也随着变化,然后两个量的比值一定,两个量就成正比例;如果两个量的乘积一定,就成反比例;由此判断即可。
【解析】收割的总面积÷收割机台数=每台收割机收割的面积,没有说明每台收割机收割的面积是否一定,所以无法判断二者的关系。原题说法正确。
故答案为:√
【点评】本题考查了辨识正比例和反比例的量,商一定是正比例,积一定是反比例。
22.×
【分析】根据比例的基本性质进行判断即可。
【解析】在比例中,两个内项分别是3和4,两个外项的积是3×4=12,所以原题说法错误。
【点评】本题考查了比例的基本性质,比例的两外项积=两内项积。
23.×
【分析】根据比例尺的意义,比例尺是图上距离与实际距离的比,把这幅图上的长10厘米化成100毫米,再用图上距离比实际距离,然后再化简。
【解析】10厘米=100毫米
100毫米∶2毫米=50∶1
答:这幅图的比例尺是50∶1。
原题说法错误。
故答案为:×。
【点评】本题主要考查了比例尺,根据比例尺的意义即可写出这幅图的比例尺,注意化成相同单位再比。
24.×
【解析】因为直角三角形的面积=两条直角边的乘积÷2,如果两条直角边都扩大4倍,面积就要扩大16倍。因此命题错误。故答案为:×
25.√
【分析】梯形的面积=(上底+下底)×高÷2,梯形的面积一定,梯形的上、下底之和与高的积就一定,积一定,梯形的上、下底之和与高成反比例,据此解答。
【解析】根据分析可得,梯形的面积一定时,上、下底之和与高成反比例。说法正确。
故答案为:√
26.0.4;206;9.7
0.99;2.4;
12;0.1
【解析】略
27.5.75;90500;1;2.1
【解析】7.28一(1.28+0.25)
=7.28一1.28-0.25
=6-0.25
=5.75
905×99+905
=905×(99+1)
=905×100
=90500
20×÷×
=20×××
=1
16.8÷[32×(1-)]
=16.8÷(32×)
=16.8÷8
=2.1
28.x=5;x=0.02;x=4.76
【分析】=,解比例,原式化为:3x=2.5×6,再用2.5×6的积除以3,即可解答。
∶x=5∶0.4,解比例,原式化为:5x=0.4×,再用0.4×的积除以5,即可解答;
2.5x-1.9×3=6.2,先算出1.9×3的和,再用6.2-1.9×3的差除以2.5,即可解答。
【解析】=
解:3x=2.5×6
3x=15
x=15÷3
x=5
∶x=5∶0.4
解:5x=0.4×
5x=0.1
x=0.1÷5
x=0.02
2.5x-1.9×3=6.2
解:2.5x-5.7=6.2
2.5x=6.2+5.7
2.5x=11.9
x=11.9÷2.5
x=4.76
29.3113cm2
【分析】观察图形可知,该图形的表面积等于长方体的表面积加上圆柱的侧面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,圆柱的侧面积公式:S=πdh,据此代入数值进行计算即可。
【解析】(20×30+20×5+30×5)×2+3.14×15×30
=(600+100+150)×2+3.14×15×30
=850×2+3.14×15×30
=1700+1413
=1700+1413
=3113(cm2)
30.见详解
【分析】根据实际距离×比例尺=图上距离,先算出图上距离,弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求的比例画出相应的长度。
【解析】300米=30000厘米,400米=40000厘米
30000÷20000=1.5(厘米)
40000÷20000=2(厘米)
【点评】关键是掌握图上距离与实际距离的换算方法,将方向和距离结合起来描述位置时,要注意三个要素:一是观测点,二是方向,三是距离。
31.2560棵
【分析】根据死亡棵数与成活棵数的比,用成活棵数÷对应份数,求出一份数,一份数×总份数=总棵数。
【解析】1760÷11×(5+11)
=160×16
=2560(棵)
答:这批沙柳树苗的总棵数是2560棵。
【点评】关键是理解比的意义,先求出一份数。
32.能,过程见详解
【分析】根据圆柱和圆锥的体积公式,求出圆柱形水槽和圆锥形容器的容积,比较即可。
【解析】60×15=900(立方厘米)
100×30÷3=1000(立方厘米)
900<1000
答:圆锥形容器能装下这些水。
【点评】关键是掌握圆柱和圆锥的体积公式,圆柱体积=底面积×高,圆锥体积=底面积×高÷3。
33.甲火车每小时行驶80千米,乙火车每小时行驶75千米。
【分析】速度=路程÷时间,由题意可知,两车相遇后又继续行驶了1.2小时,这时两车相距186千米,(1)由此可算出两车的速度之和,再根据两车的速度比是16∶15,即可算出两车的速度;(2)用方程解,设甲火车的速度为x,根据速度比是16∶15,可得出乙车的速度为,再由相遇后又继续行驶了1.2小时,这时两车相距186千米即可列出等式进行计算;据此解答。
【解析】由分析可得:
方法一:186÷1.2=155(千米)
155÷(16+15)×16=80(千米)
155÷(16+15)×15=75(千米)
方法二:设甲火车的速度为x,则乙车的速度为,有
(x+)×1.2=186
=155
x=80
=80×=75(千米)
答:甲火车每小时行驶80千米,乙火车每小时行驶75千米。
【点评】本题主要考查了比的应用,关键是要认真分析题意,找出题目中的等量关系进行解答。
34.98
【分析】周长之比就等于边长之比,设甲、乙、丙的边长为,,;根据“正方形的面积边长边长”分别求出大正方形和中正方形的面积,然后根据“大正方形的面积中正方形的面积丙的面积”列出方程,求出;进而求出大正方形的面积。
【解析】周长之比就等于边长之比,设甲、乙、丙的边长为,,。
,
;
大正方形的面积:;
答:大正方形的面积是98。
故答案为:98
【点评】解答此题的关键:根据题意,设出甲、乙、丙的边长,进而根据正方形的面积计算公式分别求出大正方形和中正方形的面积,找到等量关系,列出方程即可。
35.20∶6∶3
【分析】第一种混合物中A、B重量比与最终混合物的A、B重量比相同,均为3∶5。所以,先将第二种、第三种混合物的A、B重量比调整到3∶5,再将第二种、第三种混合物中A、B与第一种混合物中A、B视为单一物质D,然后求出新配成的物质中D∶C的比。最终确定三种混合物的重量比。
【解析】D∶C=(3+5)∶2=4∶1;
第二种混合物不含A,B的含量为,第三种混合物不含B,A的含量为,所以倍第三种混合物含A为3,倍第二种混合物含B为5,即第二种、第三种混合物的重量比为2∶1;于是此时含有C:,即C∶D=29∶(45-29)=29∶16,而最终混合物中C∶D=1∶4=29∶116,所以第一种混合物的质量与后两种混合质量和之比为(116-16)∶45=20∶9,所以三种混合物的重量比为20∶6∶3。
答:三种混合物的比为20∶6∶3。
【点评】本题主要考查了比的应用,关键是要认真分析题意,找出题目中的数量关系进行解答。
36.(1)240立方厘米;
(2)960立方厘米;
(3)26.7%
【分析】(1)根据圆柱的体积公式:V=Sh=πr2h,代入数据计算即可;
(2)露出水面部分的体积就是下降部分的水的体积,由此求得容器的底面积,从而可将求铁块的体积转化为求上升部分的水的体积,用容器的底面积乘水面上升的8cm即可;
(3)用铁块的体积除以容器的容积可以计算出百分比。
【解析】(1)3×42×5
=3×16×5
=48×5
=240(立方厘米)
答:这个铁块露出水面部分的体积是240立方厘米。
(2)240÷2×8
=120×8
=960(立方厘米)
答:这个铁块的体积是960立方厘米。
(3)960÷(120×30)
=960÷3600
≈26.7%
答:这个铁块的体积占玻璃容器容积的。
【点评】本题主要考查圆柱、长方体的体积公式的应用,解题的关键是理解“露出水面部分的体积就是下降部分的水的体积”。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点中学分班考押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.下列四个选项中,正确的是( )。
A.一个不透明的盒子里装了红、黑、白玻璃球各4个,要保证取出的玻璃球3种颜色都有,至少要取9个玻璃球。
B.如果y=5x(x、y≠0),那么x和y成反比例。
C.1枚硬币掷3次有2次正面朝上,1次反面朝上,那么掷第4次一定正面朝上。
D.等腰三角形的两边长分别为4厘米和2厘米,则这个三角形的周长是8厘米或10厘米。
2.把m+1个物体放进m个抽屉里,总有一个抽屉里至少放进( )个物体(m为大于0的自然数)。
A.m B. C.2 D.1
3.一条毛毛虫从幼虫长到成虫,每天长大一倍,22天能长到20厘米,当长到5厘米时,需要用( )天。
A.21 B.20 C.19 D.18
4.小明和小华用黑桃2-9做游戏,任意摸一张牌,不公平的是( )。
A.摸到奇数小明赢,摸到偶数小华赢。 B.摸到质数小明赢,摸到合数小华赢。
C.摸到大于5的小明赢,摸到小于5的小华赢。 D.摸到3或5的倍数小明赢,否则小华赢。
5.图示为一幅图形的密铺方案,则此阴影部分的面积和整个图形的面积比为( )。
A.4∶8 B.4∶1 C.4∶5 D.4∶11
6.著名的“洛神赋图”是东晋画家顾恺之绘制,画卷纵27.1厘米,横572.8厘米,是北京故宫博物院的珍藏品。如果一个人张开双臂大约有1.5米,大概( )个人张开双臂手拉手才有这幅画横向的长度。
A.2 B.3 C.4
7.一幅地图上,用20厘米表示380千米,则该地图的比例尺为( )。
A.1∶19000000 B.1∶1900000 C.1∶190000 D.1∶19000
8.下列各图中,能表示出两个量成正比例关系的是( )。
A. B.
C. D.
二、填空题。(每空1分,共14分)
9.一个比如果将前项增加30%,后项必须加上3比值才能不变,这个比的后项是 。
10.一条路,甲工程队20天修完,乙工程队30天修完,甲、乙的效率是 .
11.用一张长8分、4分米的长方形铁皮,做一个高为1分米的无盖铁皮盒(焊接处与铁皮厚不计),这个铁皮盒最大的容积 立方分米.
12.甲、乙、丙三名滑冰运动员在一起训练。已知,甲滑1圈时,乙能滑圈,丙能滑圈。三人同时同地出发,甲滑 圈时,三个人第一次再相遇。
13.甲、乙两城市的距离是120千米,甲、乙两城之间有一个电视塔,电视塔距甲、乙两城的距离比为1∶5,乙城和电视塔之间的距离为 千米。
14.如图,一根长2米的圆柱形木料,截去一半后,剩下的圆柱形木料的表面积比原来减少了62.8平方分米,原来圆柱形木料的底面积是 平方分米,体积是 立方分米。
15.施灵为了测量萝卜的体积,先将一个萝卜削成一个长5厘米、宽4厘米、高2厘米的长方体,并用天平称出这个长方体重20克。接着用天平称出要测量体积的萝卜重320克。这个萝卜的体积是 立方厘米。
16.在美术中,让人觉得最美的比例叫黄金比例,它的比例是1∶0.618,要让重光宝塔的高和直径成黄金比例,如果高是20m,直径应是 m。
17.图中的大圆半径等于小圆的直径。大圆周长与小圆周长的比是 。
18.某车间人数不超过100人,已知男工人数的等于女工人数的,这个车间男工与女工最多相差 人。
19.把一个高为3cm的圆柱的侧面展开得到一个长方形,这个长方形的长是12.56cm。这个圆柱的表面积是 平方厘米,体积是 立方厘米。
20.配制一种药水,在1.8千克的水中,放入200克药剂那么药剂的质量与药水总质量的比是 .
三、判断题。(每题1分,共5分)
21.收割机的台数和收割的总面积不成比例。( )
22.在比例中,两个内项分别是3和4,两个外项的和是12。( )
23.一种精密零件,长2毫米,画在一幅图上长10厘米,这幅图的比例尺是1∶50。( )
24.一个直角三角形的两条直角边都放大到原来的4倍后,面积也放大到原来的4倍。( )
25.梯形的面积一定时,上、下底之和与高成反比例。( )
四、计算题。(共33分)
26.直接写得数.(共8分)
4.8×= 598-392= 6.7+3= 1.25×0.8-1%=
5.1×= ×÷×= (3.6+7.2)÷0.9= 3.4×÷4=
27.计算下面各题.(能简算的要简算,共12分)
7.28一(1.28+0.25) 905×99+905 20×÷× 16.8÷[32×(1-)]
28.解方程或比例。(共9分)
29.计算下面图形的表面积。(共4分)
五、操作题。(共4分)
30.看图,先算出小梅家和小芳家的图上距离,再按要求在下图中标出两家的位置。
(1)小梅家在学校正南方向约300米处;
(2)小芳家在学校北偏西30°约400米处。
六、解答题。(每题6分,共36分)
31.某地为治理荒漠化,在沙漠上种植了一批沙柳树苗,1个月后树苗的死亡棵数与成活棵数的比是5∶11,如果成活了1760棵,那么这批沙柳树苗的总棵数是多少?
32.将底面积60平方厘米,高15厘米的圆柱形状水槽注满水,然后将水倒入底面积是100平方厘米,高是30厘米的圆锥形容器中。圆锥形容器能装下这些水吗?写出过程。(题目中数据都是从水槽、圆锥形容器内部测量得到的)
33.甲、乙两列火车同时从两站相对开出,相遇后又继续行驶了1.2小时,这时两车相距186千米,已知两列火车的速度比是16∶15,两车每小时各行驶多少千米?(用两种方法解)
34.如图,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和形区域乙和丙。已知三块区域甲、乙、丙的周长之比,并且区域丙的面积为48,求大正方形的面积。
35.已知三种混合物由三种成分A、B、C组成,第一种仅含成分A和B,重量比为3∶5;第二种只含成分B和C,重量比为1∶2;第三种只含成分A和C,重量之比为2∶3。以什么比例取这些混合物,才能使所得的混合物中A、B和C,这三种成分的重量比为3∶5∶2?
36.张亮在一个长方体的玻璃容器中装了一些水,他把一个底面半径为的圆柱形铁块完全浸入水中,发现水面上升了。他又把这个铁块垂直拉出水面,这时水面下降(如下图所示,玻璃厚度忽略不计)。
(1)这个铁块露出水面部分的体积是多少?(取3)
(2)这个铁块的体积是多少?(取3)
(3)这个铁块的体积占玻璃容器容积的百分之几?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】A.从最极端的情况分析,假设把红球和黑球都取完,就是取8个玻璃球,这时候,再取一个球,就可以保证取出的玻璃球3种颜色都有;
B.判断x和y之间是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例;
C.抛硬币只会出现正面朝上和反面朝上两种结果,每种结果朝上的可能性都为,不会受投掷的次数影响;
D.等腰三角形的两边长分别为4厘米和2厘米,有两种情况,腰长可能是4厘米,也可能是2厘米,当腰长是4厘米时,另一条边长是2厘米,三角形的周长是10厘米;当腰长是2厘米时,另一条边长是4厘米,周长是8厘米;但考虑三角形的三边长的关系,2+2=4,不符合三角形的三条边长的关系,所以当腰长是2厘米时不满足条件,腰长只能是4厘米。
【解析】A.4+4+1=9(个);至少要取9个玻璃球,能保证取出的玻璃球3种颜色都有。原题说法正确;
B.如果y=5x(x、y≠0),y÷x=5(一定),y和x的商一定,所以x和y成正比例,原题说法错误;
C.每次抛硬币是一个独立事件,下一次的结果不会受前一次的影响,所以可能出现1枚硬币掷3次有2次正面朝上,1次反面朝上这样的事件,但并能说明正面朝上的可能性比反面朝上的可能性大。所以原题说法错误;
D.根据分析得,腰长只能是4厘米,4+4+2=10(厘米),周长是10厘米;所以原题说法错误。
故答案为:A
【点评】此题的综合性较强,涉及各个章节的基础知识,注意平时知识的积累。
2.C
【分析】根据鸽巢原理:如果把(n+1)个物体放在n个抽屉里,那么必有一个抽屉里至少放有两个物体;据此解答即可。
【解析】由分析可得:把(m+1)个物体放进m个抽屉里,总有一个抽屉放进2个物体。
故答案为:C
【点评】本题主要考查了鸽巢原理的应用,关键是要理解巢原理。
3.B
【分析】采用倒推的方法,每天长大一倍,22天20厘米;到21天为20÷2=10厘米,20天为10÷5=5厘米,据此解答。
【解析】21天:20÷2=10(厘米)
20天:10÷2=5(厘米)
一条毛毛虫从幼虫长到成虫,每天长大一倍,22天能长到20厘米,当长到5厘米时,需要用20天。
故答案为:B
【点评】本题考查的知识点是用倒推法或者叫还原法来解答趣味数学问题,解答此题的关键条件是每天长大一倍。
4.C
【分析】在摸牌游戏中,只要双方发生的概率相等,游戏就公平,反之就不公平;据此解答。
【解析】A.2-9的数字中,奇数有3、5、7、9共4个,偶数有2、4、6、8共4个,奇数和偶数的个数相等,俩人摸到的概率相同;游戏公平;
B. 2-9的数字中,质数有2、3、5、7共4个,合数有4、6、8、9共4个,质数和合数的个数相同,俩人摸到的概率相同;游戏公平;
C. 2-9的数字中,大于5的数有6、7、8、9共4个,小于5的数有2、3、4共3个数,摸到大于5的概率比摸到小于5的概率大,游戏不公平;
D. 2-9的数字中,3或5的倍数有3、5、6、9,不是3或5的倍数有2、4、7、8,3或5的倍数与不是3或5的倍数的数的个数相同,俩人摸到的概率相同;游戏公平。
故答案为:C。
【点评】本题考查的是判断可能事件的概率的大小。
5.D
【分析】根据题图可知,整个图形可以分成11个完全相同的小三角形,阴影部分为4个小三角形,据此写出它们之间的比即可。
【解析】阴影部分的面积和整个图形的面积比为4∶11;
故答案为:D
【点评】解答本题的关键是将整个图形分成面积相等的小三角形,再进一步解答。
6.C
【分析】1米=100厘米,因此先用1.5乘100将1.5米化成厘米,然后计算出横572.8厘米的近似数,这个近似数里面大约有几个150厘米就大概有几个人张开双臂手拉手才有这幅画横向的长度。
【解析】1.5米=150厘米
572.8厘米≈573厘米;
150×4=600厘米;
573厘米≈600厘米;
因此大概4个人张开双臂手拉手才有这幅画横向的长度。
故答案为:C
【点评】此题考查的是米和厘米之间的换算、小数的近似数、整数的近似数,要熟练掌握。
7.B
【分析】比例尺=图上距离∶实际距离,据此解答。
【解析】380千米=38000000厘米
则该地图的比例尺为:20∶38000000=1∶1900000。
故选择:B
【点评】此题考查了比例尺的意义,换算单位时注意数清0的个数。
8.C
【分析】首先要知道成正比例关系的图象特点是一条经过原点的直线,相关联的两个量应是比值或商一定;据此即可作出正确选择。
【解析】A.不是一条直线,不符合题意;
B.是一条曲线,不是直线,不符合题意;
C.是一条经过原点的直线,符合题意;
D.不是一条直线,不符合题意。
故答案为:C。
【点评】本题主要考查正比例的图像,熟练掌握正比例的图像并灵活运用。
9.10
【分析】根据比的性质可知:如果比的前项增加30%,要使比值不变,那么后项也要增加30%,进而根据后项增加的30%是3,用3除以30%即得这个比的后项。
【解析】比的前项增加30%,要使比值不变,后项也要增加30%,那么3÷30%=10。
答:这个比的后项是10。
故答案为10。
【点评】解决此题关键是理解如果比的前项增加30%,要使比值不变,后项也要增加30%,进一步得解。
10.3:2.
【分析】把工作总量看作单位“1”,根据甲、乙两个工程队所用的时间,分别求出甲、乙两个工程队的工作效率,进而写出工作效率比并化简比.
【解析】甲的效率:1÷20=,
乙的效率,1,
甲、乙的效率比::=3:2;
11.12
【解析】试题分析:画图,结合图形找出长方体的长、宽、高,由体积计算公式解答即可.
解:如图,
铁皮盒的容积:
1×( 8﹣1×2)×( 4﹣1×2 ),
=1×6×2,
="12" (dm3);
答:这个铁皮盒的容积最大是12立方分米;
故答案为12.
点评:此题主要考查长方体的体积计算公式:长方体的体积=长×宽×高.
12.12
【分析】由题可得,3人的滑冰速度比为:1∶∶,化成最简整数比为:12∶16∶15。三人同时同地出发,当三人相遇时,一定是三人刚好同时回到出发点,即三人刚好同时滑了整圈数,此时甲滑了12圈。
【解析】1∶∶=12∶16∶15,当甲滑12圈时,三个人第一次再相遇。
【点评】本题考查最简整数比的应用,理解三个人何时第一次再相遇时解答此题的关键。
13.100
【分析】因为甲、乙两城之间的距离是120千米,它们之间有一个电视塔,而且电视塔距甲、乙两城的距离比为1∶5,就相当于把120千米平均分成6份,而乙城和电视塔之间的距离是6份中的5份。
【解析】120÷(1+5)×5
=120÷6×5
=20×5
=100(千米)
【点评】本题主要考查按比分配,解题关键是把总距离平均分成6份,乙城和电视塔之间的距离是其中5份。
14.3.14 62.8
【分析】减少的表面积就是截去一半圆柱的侧面积,根据底面周长=侧面积÷高,底面面积=(底面周长÷π÷2)2×π,体积=底面积×高,代入数据计算即可。
【解析】2÷2=1(米)
1米=10分米
62.8÷10÷3.14÷2
=6.28÷3.14÷2
=1(分米)
3.14×12=3.14(平方分米)
2米=20分米
3.14×20=62.8(立方分米)
【点评】这是一道关于圆柱的题目,根据圆柱的侧面积和体积公式、圆的周长和面积公式解答。
15.640
【分析】先求出长方体体积,再算出每立方厘米的重量,用总重量÷每立方厘米重量=总体积。
【解析】320÷[20÷(5×4×2)]
=320÷[20÷40]
=320÷0.5
=640(立方厘米)
【点评】本题考查了不规则物体体积的算法,通过重量求出体积,方法比较巧妙。
16.12.36
【分析】根据“它的比例是1∶0.618”,即重光宝塔的高和直径的比值是一定的,由此列出比例,解决问题。
【解析】解:设直径应是xm,
1∶0.618=20∶x
x=0.618×20
x=12.36
答:直径应是12.36m。
故答案为:12.36。
【点评】本题主要考查了比例的应用,解答此题的关键是判断出重光宝塔的高和直径成正比例。
17.2∶1
【分析】设小圆的半径是r,则小圆的直径是2r,大圆的半径是2r,根据“圆的周长=2πr”分别计算出大圆和小圆的周长,然后进行比即可。
【解析】设小圆的半径是r,则小圆的直径是2r,大圆的半径是2r,则:
[2×π×(2r)]∶(2πr)
=4πr∶2πr
=2∶1
【点评】解答此题应根据圆的周长的计算方法进行解答即可。
18.45
【分析】男工人数的等于女工人数的,所以男工人数∶女工人数=∶=8∶3,男工人数和女工人数的总份数是8+3=11,因为某车间人数不超过100人,100以内11的倍数最大是99,所以这个车间男工与女工最多相差的人数=99÷总份数×(男工人数占的人数-女工人数占的人数)。
【解析】男工人数∶女工人数=∶=8∶3
8+3=11,100以内11的倍数最大是99,99÷11×(8-3)=45,所以这个车间男工与女工最多相差45人。
19.62.8 37.68
【分析】(1)圆柱的表面积=侧面积+底面积×2;圆柱的侧面积=底面周长×高;本题圆柱侧面展开是一个长方形,长方形的长就是圆柱的底面周长。先用底面周长求出圆柱的底面半径,然后求出底面积,再求出圆柱侧面积,最后求出圆柱的表面积。
(2)圆柱的体积=底面积×高,先用底面周长求出圆柱的底面半径,然后用体积公式求出圆柱的体积。
【解析】(1)12.56÷3.14÷2=2(厘米)
3.14×2 ×2=25.12(平方厘米)
12.56×3=37.68(平方厘米)
25.12+37.68=62.8(平方厘米)
(2)12.56÷3.14÷2=2(厘米)
3.14×2 ×3=37.68(立方厘米)
20.1∶10
【解析】略
21.√
【分析】两个相关联的量,一个量变化另一个量也随着变化,然后两个量的比值一定,两个量就成正比例;如果两个量的乘积一定,就成反比例;由此判断即可。
【解析】收割的总面积÷收割机台数=每台收割机收割的面积,没有说明每台收割机收割的面积是否一定,所以无法判断二者的关系。原题说法正确。
故答案为:√
【点评】本题考查了辨识正比例和反比例的量,商一定是正比例,积一定是反比例。
22.×
【分析】根据比例的基本性质进行判断即可。
【解析】在比例中,两个内项分别是3和4,两个外项的积是3×4=12,所以原题说法错误。
【点评】本题考查了比例的基本性质,比例的两外项积=两内项积。
23.×
【分析】根据比例尺的意义,比例尺是图上距离与实际距离的比,把这幅图上的长10厘米化成100毫米,再用图上距离比实际距离,然后再化简。
【解析】10厘米=100毫米
100毫米∶2毫米=50∶1
答:这幅图的比例尺是50∶1。
原题说法错误。
故答案为:×。
【点评】本题主要考查了比例尺,根据比例尺的意义即可写出这幅图的比例尺,注意化成相同单位再比。
24.×
【解析】因为直角三角形的面积=两条直角边的乘积÷2,如果两条直角边都扩大4倍,面积就要扩大16倍。因此命题错误。故答案为:×
25.√
【分析】梯形的面积=(上底+下底)×高÷2,梯形的面积一定,梯形的上、下底之和与高的积就一定,积一定,梯形的上、下底之和与高成反比例,据此解答。
【解析】根据分析可得,梯形的面积一定时,上、下底之和与高成反比例。说法正确。
故答案为:√
26.0.4;206;9.7
0.99;2.4;
12;0.1
【解析】略
27.5.75;90500;1;2.1
【解析】7.28一(1.28+0.25)
=7.28一1.28-0.25
=6-0.25
=5.75
905×99+905
=905×(99+1)
=905×100
=90500
20×÷×
=20×××
=1
16.8÷[32×(1-)]
=16.8÷(32×)
=16.8÷8
=2.1
28.x=5;x=0.02;x=4.76
【分析】=,解比例,原式化为:3x=2.5×6,再用2.5×6的积除以3,即可解答。
∶x=5∶0.4,解比例,原式化为:5x=0.4×,再用0.4×的积除以5,即可解答;
2.5x-1.9×3=6.2,先算出1.9×3的和,再用6.2-1.9×3的差除以2.5,即可解答。
【解析】=
解:3x=2.5×6
3x=15
x=15÷3
x=5
∶x=5∶0.4
解:5x=0.4×
5x=0.1
x=0.1÷5
x=0.02
2.5x-1.9×3=6.2
解:2.5x-5.7=6.2
2.5x=6.2+5.7
2.5x=11.9
x=11.9÷2.5
x=4.76
29.3113cm2
【分析】观察图形可知,该图形的表面积等于长方体的表面积加上圆柱的侧面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,圆柱的侧面积公式:S=πdh,据此代入数值进行计算即可。
【解析】(20×30+20×5+30×5)×2+3.14×15×30
=(600+100+150)×2+3.14×15×30
=850×2+3.14×15×30
=1700+1413
=1700+1413
=3113(cm2)
30.见详解
【分析】根据实际距离×比例尺=图上距离,先算出图上距离,弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求的比例画出相应的长度。
【解析】300米=30000厘米,400米=40000厘米
30000÷20000=1.5(厘米)
40000÷20000=2(厘米)
【点评】关键是掌握图上距离与实际距离的换算方法,将方向和距离结合起来描述位置时,要注意三个要素:一是观测点,二是方向,三是距离。
31.2560棵
【分析】根据死亡棵数与成活棵数的比,用成活棵数÷对应份数,求出一份数,一份数×总份数=总棵数。
【解析】1760÷11×(5+11)
=160×16
=2560(棵)
答:这批沙柳树苗的总棵数是2560棵。
【点评】关键是理解比的意义,先求出一份数。
32.能,过程见详解
【分析】根据圆柱和圆锥的体积公式,求出圆柱形水槽和圆锥形容器的容积,比较即可。
【解析】60×15=900(立方厘米)
100×30÷3=1000(立方厘米)
900<1000
答:圆锥形容器能装下这些水。
【点评】关键是掌握圆柱和圆锥的体积公式,圆柱体积=底面积×高,圆锥体积=底面积×高÷3。
33.甲火车每小时行驶80千米,乙火车每小时行驶75千米。
【分析】速度=路程÷时间,由题意可知,两车相遇后又继续行驶了1.2小时,这时两车相距186千米,(1)由此可算出两车的速度之和,再根据两车的速度比是16∶15,即可算出两车的速度;(2)用方程解,设甲火车的速度为x,根据速度比是16∶15,可得出乙车的速度为,再由相遇后又继续行驶了1.2小时,这时两车相距186千米即可列出等式进行计算;据此解答。
【解析】由分析可得:
方法一:186÷1.2=155(千米)
155÷(16+15)×16=80(千米)
155÷(16+15)×15=75(千米)
方法二:设甲火车的速度为x,则乙车的速度为,有
(x+)×1.2=186
=155
x=80
=80×=75(千米)
答:甲火车每小时行驶80千米,乙火车每小时行驶75千米。
【点评】本题主要考查了比的应用,关键是要认真分析题意,找出题目中的等量关系进行解答。
34.98
【分析】周长之比就等于边长之比,设甲、乙、丙的边长为,,;根据“正方形的面积边长边长”分别求出大正方形和中正方形的面积,然后根据“大正方形的面积中正方形的面积丙的面积”列出方程,求出;进而求出大正方形的面积。
【解析】周长之比就等于边长之比,设甲、乙、丙的边长为,,。
,
;
大正方形的面积:;
答:大正方形的面积是98。
故答案为:98
【点评】解答此题的关键:根据题意,设出甲、乙、丙的边长,进而根据正方形的面积计算公式分别求出大正方形和中正方形的面积,找到等量关系,列出方程即可。
35.20∶6∶3
【分析】第一种混合物中A、B重量比与最终混合物的A、B重量比相同,均为3∶5。所以,先将第二种、第三种混合物的A、B重量比调整到3∶5,再将第二种、第三种混合物中A、B与第一种混合物中A、B视为单一物质D,然后求出新配成的物质中D∶C的比。最终确定三种混合物的重量比。
【解析】D∶C=(3+5)∶2=4∶1;
第二种混合物不含A,B的含量为,第三种混合物不含B,A的含量为,所以倍第三种混合物含A为3,倍第二种混合物含B为5,即第二种、第三种混合物的重量比为2∶1;于是此时含有C:,即C∶D=29∶(45-29)=29∶16,而最终混合物中C∶D=1∶4=29∶116,所以第一种混合物的质量与后两种混合质量和之比为(116-16)∶45=20∶9,所以三种混合物的重量比为20∶6∶3。
答:三种混合物的比为20∶6∶3。
【点评】本题主要考查了比的应用,关键是要认真分析题意,找出题目中的数量关系进行解答。
36.(1)240立方厘米;
(2)960立方厘米;
(3)26.7%
【分析】(1)根据圆柱的体积公式:V=Sh=πr2h,代入数据计算即可;
(2)露出水面部分的体积就是下降部分的水的体积,由此求得容器的底面积,从而可将求铁块的体积转化为求上升部分的水的体积,用容器的底面积乘水面上升的8cm即可;
(3)用铁块的体积除以容器的容积可以计算出百分比。
【解析】(1)3×42×5
=3×16×5
=48×5
=240(立方厘米)
答:这个铁块露出水面部分的体积是240立方厘米。
(2)240÷2×8
=120×8
=960(立方厘米)
答:这个铁块的体积是960立方厘米。
(3)960÷(120×30)
=960÷3600
≈26.7%
答:这个铁块的体积占玻璃容器容积的。
【点评】本题主要考查圆柱、长方体的体积公式的应用,解题的关键是理解“露出水面部分的体积就是下降部分的水的体积”。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
