2024-2025学年北师大版八下数学期末模拟试卷(含解析)
文档属性
| 名称 | 2024-2025学年北师大版八下数学期末模拟试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 891.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年北师大版八下数学期末模拟试卷
满分120分 时间120分钟
一.选择题(每小题3分,共12分)
1.(2024秋 思明区期末)要使分式有意义,则x应满足的条件是( )
A.x≠﹣3 B.x≠﹣1 C.x≠0 D.x≠1
2.(2024秋 锦江区校级期末)下列不等式变形正确的是( )
A.由a>b,得am>bm B.由a>b,得a﹣2024<b﹣2024
C.由ab>ac,得b<c D.由,得b>c
3.(2024秋 凤阳县期末)如图,在△ABC中,ED是AB的垂直平分线,AD=3,△ACE的周长为9.5,则△ABC的周长为( )
A.10.5 B.12.5 C.14.5 D.15.5
4.(2024秋 西安期末)下列各式不能运用平方差公式进行因式分解的是( )
A.﹣a2+b2 B.﹣x2﹣y2 C.49x2﹣z2 D.16m2﹣25n2
5.(2024秋 怀仁市期末)综合与实践活动小组的四位同学帮助某景区完成景区项目策划方案,需要解决下面的项目问题:如图,在该景区一块三角形绿地ABC的道路AB上建一个休息点M,使它到AC和BC两边的距离相等,在图中确定休息点M的位置.下列方案能满足项目要求的是( )
A.B. C.D.
6.(2024春 孝感期末)若关于x的不等式组的整数解有且只有3个,则m的取值范围为( )
A.m≥﹣1 B.m<1 C.0≤m<1 D.0<m≤1
7.(2024秋 任城区期末)如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为( )cm2
题7 题9 题12
A.6 B.9 C.18 D.24
8.(2024秋 香河县期末)如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
9.(2024秋 临淄区期末)如图4×4的正方形网格中,其中一个三角形①绕某点旋转一定的角度,得到三角形②,则其旋转中心是( )
A.点A B.点B C.点C D.点D
10.(2024秋 孝昌县期末)已知x2﹣3x+2=0,则( )
A.1 B.2 C.3 D.4
11.(2024秋 青山湖区校级期末)▲若分式方程有增根,则m的值为( )
A.2 B.4 C.2或﹣2 D.4或﹣8
12.(2024秋 福山区期末)如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
二.填空题(每小题4分,共24分)
13.(2022秋 渌口区期末)若分式的值为0,则x的值为 .
14.(2024春 五华县期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 .
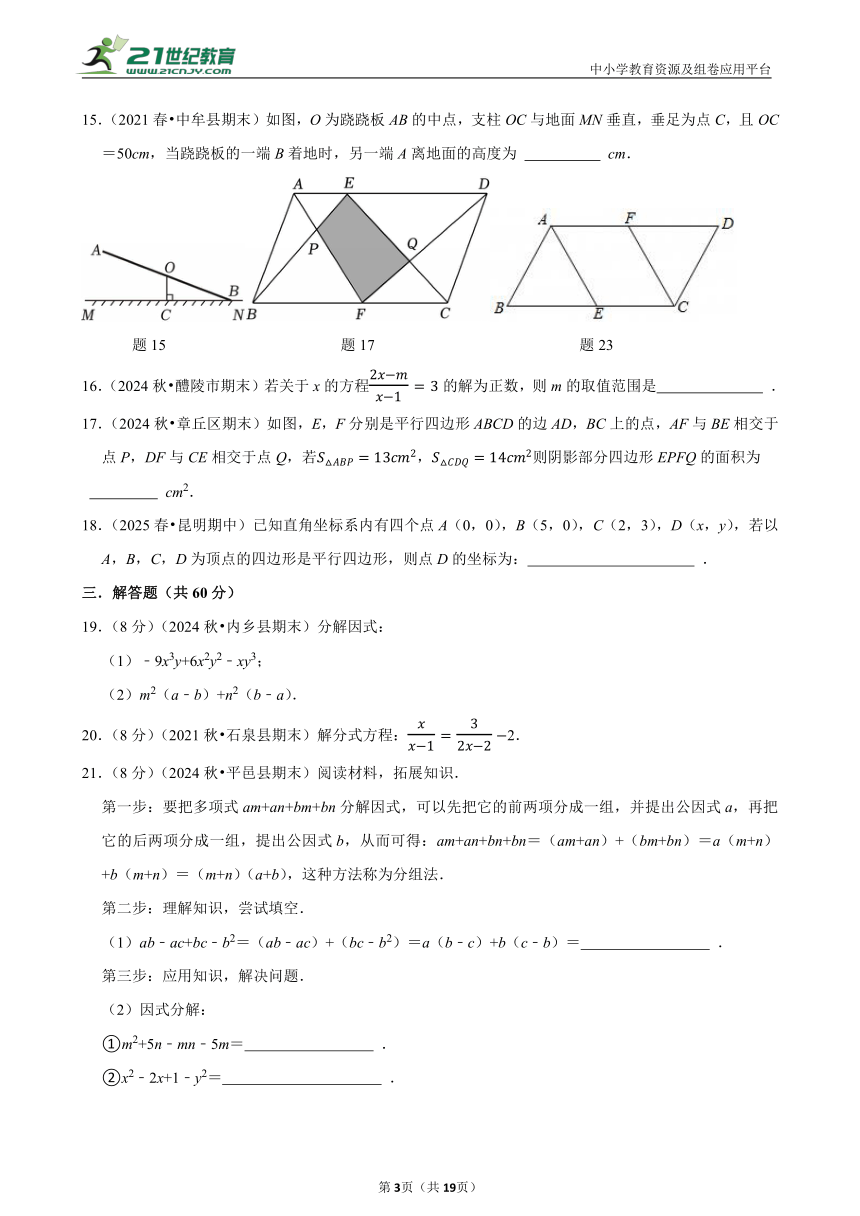
15.(2021春 中牟县期末)如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为 cm.
题15 题17 题23
16.(2024秋 醴陵市期末)若关于x的方程的解为正数,则m的取值范围是 .
17.(2024秋 章丘区期末)如图,E,F分别是平行四边形ABCD的边AD,BC上的点,AF与BE相交于点P,DF与CE相交于点Q,若,则阴影部分四边形EPFQ的面积为
cm2.
18.(2025春 昆明期中)已知直角坐标系内有四个点A(0,0),B(5,0),C(2,3),D(x,y),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为: .
三.解答题(共60分)
19.(8分)(2024秋 内乡县期末)分解因式:
(1)﹣9x3y+6x2y2﹣xy3;
(2)m2(a﹣b)+n2(b﹣a).
20.(8分)(2021秋 石泉县期末)解分式方程:2.
21.(8分)(2024秋 平邑县期末)阅读材料,拓展知识.
第一步:要把多项式am+an+bm+bn分解因式,可以先把它的前两项分成一组,并提出公因式a,再把它的后两项分成一组,提出公因式b,从而可得:am+an+bn+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b),这种方法称为分组法.
第二步:理解知识,尝试填空.
(1)ab﹣ac+bc﹣b2=(ab﹣ac)+(bc﹣b2)=a(b﹣c)+b(c﹣b)= .
第三步:应用知识,解决问题.
(2)因式分解:
①m2+5n﹣mn﹣5m= .
②x2﹣2x+1﹣y2= .
第四步:提炼思想,拓展应用.
(3)已知三角形的三边长分别是a、b、c,且满足a2+2b2+c2=2b(a+c),试判断这个三角形的形状,并说明理由.
22.(8分)(2025 龙凤区校级三模)先化简,再求值:,其中.
23.(8分)(2025 镇江模拟)如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)若AE=CE,BC=2AB,BC=6,求四边形AECF的面积.
24.(10分)(2025 成都)2025年8月7日至17日,第12届世界运动会将在成都举行,与运动会吉祥物“蜀宝”“锦仔”相关的文创产品深受大家喜爱.某文旅中心在售A,B两种吉祥物挂件,已知每个B种挂件的价格是每个A种挂件价格的,用300元购买B种挂件的数量比用200元购买A种挂件的数量多7个.
(1)求每个A种挂件的价格;
(2)某游客计划用不超过600元购买A,B两种挂件,且购买B种挂件的数量比A种挂件的数量多5个,求该游客最多购买多少个A种挂件.
25.(10分)(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
2024-2025学年北师大版八下数学期末模拟试卷
参考答案与试题解析
一.选择题
1.(2024秋 思明区期末)要使分式有意义,则x应满足的条件是( )
A.x≠﹣3 B.x≠﹣1 C.x≠0 D.x≠1
【答案】D
【分析】根据分式的分母不为零求解即可.
【解答】解:要使分式有意义,只须x﹣1≠0,即x≠1,
故选:D.
2.(2024秋 锦江区校级期末)下列不等式变形正确的是( )
A.由a>b,得am>bm
B.由a>b,得a﹣2024<b﹣2024
C.由ab>ac,得b<c
D.由,得b>c
【答案】D
【分析】不等式的基本性质:(1)等式的两边同时加上或减去同一个数或字母,不等号方向不变;(2)等式的两边同时乘以或除以同一个正数,不等号方向不变;(3)等式的两边同时乘以或除以同一个负数,不等号方向改变.据此逐项分析判断即可.
【解答】解:根据不等式的基本性质逐项分析判断如下:
A.由a>b,若m>0,则可得am>bm,故本选项变形错误,不符合题意;
B.由a>b,得a﹣2024>b﹣2024,故本选项变形错误,不符合题意;
C.由ab>ac,若a<0,则可得b<c,故本选项变形错误,不符合题意;
D. ,因为a2+1>0,所以可得b>c,故本选项变形正确,符合题意.
故选:D.
3.(2024秋 凤阳县期末)如图,在△ABC中,ED是AB的垂直平分线,AD=3,△ACE的周长为9.5,则△ABC的周长为( )
A.10.5 B.12.5 C.14.5 D.15.5
【答案】D
【分析】先利用线段垂直平分线的性质可得:BD=AD=3,EA=EB,AB=2AD=6,然后利用等量代换和三角形的周长公式进行计算,即可解答.
【解答】解:∵ED是AB的垂直平分线,AD=3,
∴BD=AD=3,EA=EB,AB=2AD=6,
∵△ACE的周长为9.5
∴AC+AE+EC=9.5,
∴AC+BE+EC=9.5,
∴AC+BC=9.5,
∴△ABC的周长为AB+AC+BC=9.5+6=15.5,
故选:D.
4.(2024秋 西安期末)下列各式不能运用平方差公式进行因式分解的是( )
A.﹣a2+b2 B.﹣x2﹣y2 C.49x2﹣z2 D.16m2﹣25n2
【答案】B
【分析】根据平方差公式的公式结构对各选项分析判断后利用排除法求解.
【解答】解:A、﹣a2+b2符合平方差公式结构,故本选项不合题意;
B、﹣x2﹣y2不符合平方差公式结构,故本选项符合题意;
C、49x2﹣z2符合平方差公式结构,故本选项不合题意;
D、16m2﹣25n2符合平方差公式结构,故本选项不合题意.
故选:B.
5.(2024秋 怀仁市期末)综合与实践活动小组的四位同学帮助某景区完成景区项目策划方案,需要解决下面的项目问题:如图,在该景区一块三角形绿地ABC的道路AB上建一个休息点M,使它到AC和BC两边的距离相等,在图中确定休息点M的位置.下列方案能满足项目要求的是( )
A. B.
C. D.
【答案】C
【分析】根据角平分线的性质、基本尺规作图判断即可.
【解答】解:∵点M到AC和BC两边的距离相等,且点M在AB上
∴点M是∠ACB的平分线与AB的交点,
∴C选项中的方案能满足项目要求,
故选:C.
6.(2024春 孝感期末)若关于x的不等式组的整数解有且只有3个,则m的取值范围为( )
A.m≥﹣1 B.m<1 C.0≤m<1 D.0<m≤1
【答案】C
【分析】根据解一元一次不等式组的步骤,表示出不等式组的解集,再根据整数解有且只有3个,得出关于m的不等式组即可解决问题.
【解答】解:解不等式x﹣m>0得,
x>m,
解不等式2x﹣3≥3(x﹣2)得,
x≤3,
因为不等式组的整数解有且只有3个,
所以0≤m<1.
故选:C.
7.(2024秋 任城区期末)如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为( )cm2
A.6 B.9 C.18 D.24
【答案】C
【分析】根据平移的性质求出空白部分的长和宽,根据矩形的面积公式计算,得到答案.
【解答】解:由平移的性质可知,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
则阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故选:C.
8.(2024秋 香河县期末)如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
【答案】B
【分析】根据分式的基本性质,进行作答,即可求解;
【解答】解:根据分式的基本性质可得:
,
分子扩大为原来的4倍,分母扩大为原来的2倍,因此分式的值整体扩大2倍;
故选:B.
9.(2024秋 临淄区期末)如图4×4的正方形网格中,其中一个三角形①绕某点旋转一定的角度,得到三角形②,则其旋转中心是( )
A.点A B.点B C.点C D.点D
【答案】B
【分析】根据旋转的性质,找出两组对应顶点的连线的垂直平分线,交点即为旋转中心.
【解答】解:如图:作出三角形①和三角形②两组对应点所连线段的垂直平分线的交点B为旋转中心.
故选:B.
10.(2024秋 孝昌县期末)已知x2﹣3x+2=0,则( )
A.1 B.2 C.3 D.4
【答案】C
【分析】将x2﹣3x+2=0两边分别除以x,进行求解即可.
【解答】解:∵x≠0,
∴,
∴,
∴;
故选:C.
11.(2024秋 青山湖区校级期末)▲若分式方程有增根,则m的值为( )
A.2 B.4 C.2或﹣2 D.4或﹣8
【答案】D
【分析】先根据解分式方程的方法求得m=3x﹣2,然后再根据分式方程有增根,可得x2﹣4=0,解得x=±2,把x的值代入3x﹣2进行计算即可.
【解答】解:去分母,得:m﹣2(x﹣2)=x+2,
去括号,得:m﹣2x+4=x+2,
移项、合并同类项,得:m=3x﹣2,
∵分式方程有增根,
∴x2﹣4=0,
∴x=±2,
当x=2时,m=3×2﹣2=4;
当x=﹣2时,m=3×(﹣2)﹣2=﹣8,
∴m的值可能为4或﹣8.
故选:D.
12.(2024秋 福山区期末)如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
【答案】A
【分析】根据三角形中位线定理得到△A1B1C1的周长a,△A2B2C2的周长aa,总结规律,根据规律解答即可.
【解答】解:∵点A1、B1、C1分别为BC、AC、AB的中点,
∴B1C1BC,A1C1AC,A1B1AB,
∴△A1B1C1的周长a,
同理,△A2B2C2的周长aa,
……
则△AnBn n的周长a,
故选:A.
二.填空题
13.(2022秋 渌口区期末)若分式的值为0,则x的值为 ﹣4 .
【答案】﹣4.
【分析】分式的值为零时,分子等于零,分母不等于零.
【解答】解:依题意,得:
|x|﹣4=0且x﹣4≠0,
解得x=﹣4.
故答案为:﹣4.
14.(2024春 五华县期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 12 .
【答案】见试题解答内容
【分析】根据多边形的外角和是360度即可求得外角的个数,即多边形的边数.
【解答】解:多边形的边数是:360°÷30°=12.
故答案为:12.
15.(2021春 中牟县期末)如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为 100 cm.
【答案】见试题解答内容
【分析】判断出OC是△ABD的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得AD=2OC.
【解答】解:如图,过点A作AD⊥MN于点D,则AD∥OC.
∵O是AB的中点,
∴OC是△ABD的中位线,
∴AD=2OC=2×50=100(cm).
故答案为:100.
16.(2024秋 醴陵市期末)若关于x的方程的解为正数,则m的取值范围是 m<3且m≠2 .
【答案】m<3且m≠2.
【分析】先解关于x的分式方程,它的解x用含量m的代数式表示,再根据“原分式方程有解”和“方程的解是正数”建立关于m的不等式,求解即可.
【解答】解:,
解得:x=3﹣m,
∵原分式方程有解,
∴x﹣1≠0,即3﹣m≠1(求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值,这个值叫方程的解),
解得:m≠2,
∵方程的解是正数,
∴3﹣m>0,
解得:m<3,
∴m<3且m≠2,
故答案为:m<3且m≠2.
17.(2024秋 章丘区期末)如图,E,F分别是平行四边形ABCD的边AD,BC上的点,AF与BE相交于点P,DF与CE相交于点Q,若,则阴影部分四边形EPFQ的面积为 27 cm2.
【答案】27.
【分析】连接EF,由三角形的面积公式我们可以推出S△EFC=S△DCF,S△BFE=S△BFA所以S△EFQ=S△DCQ,S△EFP=S△ABP,因此可以推出阴影部分的面积就是S四边形EPFQ=S△ABP+S△DCQ,解答此题关键是作出辅助线,找出同底等高的三角形.
【解答】解:如图,连接EF,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△DCF的FC边上的高相等,
∴S△EFC=S△DCF,
∴S△EFQ=S△DCQ,
同理S△BFE=S△BFA,
∴S△EFP=S△ABP,
∵,,
∴,
故答案为:27.
18.(2025春 昆明期中)已知直角坐标系内有四个点A(0,0),B(5,0),C(2,3),D(x,y),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为: (3,﹣3)或(﹣3,3)或(7,3) .
【答案】(3,﹣3)或(﹣3,3)或(7,3).
【分析】由平行四边形的性质和中点坐标公式可求解.
【解答】解:①当AB为对角线时,中点坐标为(,),即(,0),
根据平行四边形的性质,得,0,
解得x=3,y=﹣3,
∴点D的坐标为(3,﹣3);
②当AC为对角线时,中点坐标为(,),即(1,),
根据平行四边形的性质,得1,
解得x=﹣3,y=3,
∴点D的坐标为(﹣3,3);
③当BC为对角线时,中点坐标为(,),即(,),
根据平行四边形的性质,得,
解得x=7,y=3,
∴点D的坐标为(7,3);
故答案为:(3,﹣3)或(﹣3,3)或(7,3).
三.解答题
19.(2024秋 内乡县期末)分解因式:
(1)﹣9x3y+6x2y2﹣xy3;
(2)m2(a﹣b)+n2(b﹣a).
【答案】(1)﹣xy(3x﹣y)2;
(2)(a﹣b)(m+n)(m﹣n).
【分析】(1)先提公因式,再利用完全平方公式分解因式即可;
(2)先变形,再提公因式,然后利用平方差公式分解因式即可.
【解答】解:(1)﹣9x3y+6x2y2﹣xy3
=﹣xy(9x2﹣6xy+y2)
=﹣xy(3x﹣y)2;
(2)m2(a﹣b)+n2(b﹣a)
=m2(a﹣b)﹣n2(a﹣b)
=(a﹣b)(m2﹣n2)
=(a﹣b)(m+n)(m﹣n).
20.(2021秋 石泉县期末)解分式方程:2.
【答案】见试题解答内容
【分析】先把分式方程变成整式方程,求出方程的解,最后进行检验即可.
【解答】解:方程两边都乘以2(x﹣1)得:2x=3﹣4(x﹣2),
解得:x,
检验:把x代入2(x﹣1)≠0,
所以x是原方程的解,
所以原方程的解为x.
21.(2024秋 平邑县期末)阅读材料,拓展知识.
第一步:要把多项式am+an+bm+bn分解因式,可以先把它的前两项分成一组,并提出公因式a,再把它的后两项分成一组,提出公因式b,从而可得:am+an+bn+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b),这种方法称为分组法.
第二步:理解知识,尝试填空.
(1)ab﹣ac+bc﹣b2=(ab﹣ac)+(bc﹣b2)=a(b﹣c)+b(c﹣b)= (b﹣c)(a﹣b) .
第三步:应用知识,解决问题.
(2)因式分解:
①m2+5n﹣mn﹣5m= (m﹣n)(m﹣5) .
②x2﹣2x+1﹣y2= (x﹣1+y)(x﹣1﹣y) .
第四步:提炼思想,拓展应用.
(3)已知三角形的三边长分别是a、b、c,且满足a2+2b2+c2=2b(a+c),试判断这个三角形的形状,并说明理由.
【答案】(1)(b﹣c)(a﹣b);
(2)①(m﹣n)(m﹣5);②(x﹣1+y)(x﹣1﹣y);
(3)这个三角形为等边三角形,理由见解析.
【分析】(1)仿照例题,先分组,再利用提取公因式法分解即可;
(2)①先分组,用提取公因式法分解,再用平方差公式分解即可;
②先分组,用提取公因式法分解,再用平方差公式分解即可;
(3)移项后分解因式,可得出a=b=c,则可得出答案.
【解答】解:(1)ab﹣ac+bc﹣b2
=(ab﹣ac)+(bc﹣b2)
=a(b﹣c)﹣b(b﹣c)
=(b﹣c)(a﹣b),
故答案为:(b﹣c)(a﹣b);
(2)①m2+5n﹣mn﹣5m
=m2﹣mn+5n﹣5m
=m(m﹣n)+5(n﹣m)
=m(m﹣n)﹣5(m﹣n)
=(m﹣n)(m﹣5);
②x2﹣2x+1﹣y2
=(x2﹣2x+1)﹣y2
=(x﹣1)2﹣y2
=(x﹣1+y)(x﹣1﹣y);
(3)这个三角形为等边三角形.
理由如下:
∵a2+2b2+c2=2b(a+c),
∴a2+2b2+c2﹣2ba﹣2bc=0,
∴a2﹣2ba+b2+c2﹣2bc+b2=0,
∴(a﹣b)2+(b﹣c)2=0,
∵(a﹣b)2≥0,(b﹣c)2≥0,
∴a﹣b=0,b﹣c=0,
∴a=b=c,
∴这个三角形是等边三角形.
22.(2025 龙凤区校级三模)先化简,再求值:,其中.
【答案】,.
【分析】先通分括号内的式子,同时将除法转化为乘法,再约分,然后将a的值代入化简后的式子计算即可.
【解答】解:
,
当a1时,原式.
23.(2025 镇江模拟)如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)若AE=CE,BC=2AB,BC=6,求四边形AECF的面积.
【答案】见试题解答内容
【分析】(1)根据平行四边形的性质得出AB=CD,BC=AD,∠B=∠D,求出BE=DF,根据全等三角形的判定推出即可;
(2)求出△ABE是等边三角形,求出高AH的长,再求出面积即可.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠D,
∵点E、F分别是BC、AD的中点,
∴BEBC,DFAD,
∴BE=DF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS);
(2)解:作AH⊥BC于H,
∵BC=2AB=6,E为BC中点,F为AD的中点,
∴AB=BE=CE=AF=DF=3,
∴四边形AECF是平行四边形,
∵AE=EC,
∴AE=AB=BE=CE=3,
∴△ABE是等边三角形,
∴∠B=60°,
∴AH=AB×sin60°=3,
∴四边形AECF的面积是CE×AH=3.
24.(2025 成都)2025年8月7日至17日,第12届世界运动会将在成都举行,与运动会吉祥物“蜀宝”“锦仔”相关的文创产品深受大家喜爱.某文旅中心在售A,B两种吉祥物挂件,已知每个B种挂件的价格是每个A种挂件价格的,用300元购买B种挂件的数量比用200元购买A种挂件的数量多7个.
(1)求每个A种挂件的价格;
(2)某游客计划用不超过600元购买A,B两种挂件,且购买B种挂件的数量比A种挂件的数量多5个,求该游客最多购买多少个A种挂件.
【答案】(1)每个A种挂件的价格为25元;(2)该游客最多购买11个A种挂件.
【分析】(1)依据题意,设每个A种挂件的价格为x元,则每个B种挂件的价格为x元,可得7,求出x后即可判断得解;
(2)依据题意,设该游客最多购买m个A种挂件,则购买(m+5)个B种挂件,又结合(1)每个A种挂件的价格为25元,每个B种挂件的价格为25=20元,可得25m+20(m+5)≤600,进而计算可以判断得解.
【解答】解:(1)由题意,设每个A种挂件的价格为x元,
则每个B种挂件的价格为x元,
∴7.
∴x=25.
经检验:x=25是原方程的根.
答:每个A种挂件的价格为25元.
(2)由题意,设该游客最多购买m个A种挂件,
则购买(m+5)个B种挂件,
又结合(1)每个A种挂件的价格为25元,每个B种挂件的价格为25=20元,
∴25m+20(m+5)≤600.
∴m11.
又∵m为整数,
∴m=11,则该游客最多购买11个A种挂件.
25.(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
【答案】(1)证明见解答过程;
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
【分析】(1)根据小明的作法知,CF=AE,根据平行四边形的性质求出AD∥BC,根据“一组对边平行且相等的四边形是平行四边形”求出四边形AFCE是平行四边形,根据“平行四边形的对边互相平行”即可得证;
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
【解答】(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE;
(2)解:以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
第1页(共1页)
2024-2025学年北师大版八下数学期末模拟试卷
满分120分 时间120分钟
一.选择题(每小题3分,共12分)
1.(2024秋 思明区期末)要使分式有意义,则x应满足的条件是( )
A.x≠﹣3 B.x≠﹣1 C.x≠0 D.x≠1
2.(2024秋 锦江区校级期末)下列不等式变形正确的是( )
A.由a>b,得am>bm B.由a>b,得a﹣2024<b﹣2024
C.由ab>ac,得b<c D.由,得b>c
3.(2024秋 凤阳县期末)如图,在△ABC中,ED是AB的垂直平分线,AD=3,△ACE的周长为9.5,则△ABC的周长为( )
A.10.5 B.12.5 C.14.5 D.15.5
4.(2024秋 西安期末)下列各式不能运用平方差公式进行因式分解的是( )
A.﹣a2+b2 B.﹣x2﹣y2 C.49x2﹣z2 D.16m2﹣25n2
5.(2024秋 怀仁市期末)综合与实践活动小组的四位同学帮助某景区完成景区项目策划方案,需要解决下面的项目问题:如图,在该景区一块三角形绿地ABC的道路AB上建一个休息点M,使它到AC和BC两边的距离相等,在图中确定休息点M的位置.下列方案能满足项目要求的是( )
A.B. C.D.
6.(2024春 孝感期末)若关于x的不等式组的整数解有且只有3个,则m的取值范围为( )
A.m≥﹣1 B.m<1 C.0≤m<1 D.0<m≤1
7.(2024秋 任城区期末)如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为( )cm2
题7 题9 题12
A.6 B.9 C.18 D.24
8.(2024秋 香河县期末)如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
9.(2024秋 临淄区期末)如图4×4的正方形网格中,其中一个三角形①绕某点旋转一定的角度,得到三角形②,则其旋转中心是( )
A.点A B.点B C.点C D.点D
10.(2024秋 孝昌县期末)已知x2﹣3x+2=0,则( )
A.1 B.2 C.3 D.4
11.(2024秋 青山湖区校级期末)▲若分式方程有增根,则m的值为( )
A.2 B.4 C.2或﹣2 D.4或﹣8
12.(2024秋 福山区期末)如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
二.填空题(每小题4分,共24分)
13.(2022秋 渌口区期末)若分式的值为0,则x的值为 .
14.(2024春 五华县期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 .
15.(2021春 中牟县期末)如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为 cm.
题15 题17 题23
16.(2024秋 醴陵市期末)若关于x的方程的解为正数,则m的取值范围是 .
17.(2024秋 章丘区期末)如图,E,F分别是平行四边形ABCD的边AD,BC上的点,AF与BE相交于点P,DF与CE相交于点Q,若,则阴影部分四边形EPFQ的面积为
cm2.
18.(2025春 昆明期中)已知直角坐标系内有四个点A(0,0),B(5,0),C(2,3),D(x,y),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为: .
三.解答题(共60分)
19.(8分)(2024秋 内乡县期末)分解因式:
(1)﹣9x3y+6x2y2﹣xy3;
(2)m2(a﹣b)+n2(b﹣a).
20.(8分)(2021秋 石泉县期末)解分式方程:2.
21.(8分)(2024秋 平邑县期末)阅读材料,拓展知识.
第一步:要把多项式am+an+bm+bn分解因式,可以先把它的前两项分成一组,并提出公因式a,再把它的后两项分成一组,提出公因式b,从而可得:am+an+bn+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b),这种方法称为分组法.
第二步:理解知识,尝试填空.
(1)ab﹣ac+bc﹣b2=(ab﹣ac)+(bc﹣b2)=a(b﹣c)+b(c﹣b)= .
第三步:应用知识,解决问题.
(2)因式分解:
①m2+5n﹣mn﹣5m= .
②x2﹣2x+1﹣y2= .
第四步:提炼思想,拓展应用.
(3)已知三角形的三边长分别是a、b、c,且满足a2+2b2+c2=2b(a+c),试判断这个三角形的形状,并说明理由.
22.(8分)(2025 龙凤区校级三模)先化简,再求值:,其中.
23.(8分)(2025 镇江模拟)如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)若AE=CE,BC=2AB,BC=6,求四边形AECF的面积.
24.(10分)(2025 成都)2025年8月7日至17日,第12届世界运动会将在成都举行,与运动会吉祥物“蜀宝”“锦仔”相关的文创产品深受大家喜爱.某文旅中心在售A,B两种吉祥物挂件,已知每个B种挂件的价格是每个A种挂件价格的,用300元购买B种挂件的数量比用200元购买A种挂件的数量多7个.
(1)求每个A种挂件的价格;
(2)某游客计划用不超过600元购买A,B两种挂件,且购买B种挂件的数量比A种挂件的数量多5个,求该游客最多购买多少个A种挂件.
25.(10分)(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
2024-2025学年北师大版八下数学期末模拟试卷
参考答案与试题解析
一.选择题
1.(2024秋 思明区期末)要使分式有意义,则x应满足的条件是( )
A.x≠﹣3 B.x≠﹣1 C.x≠0 D.x≠1
【答案】D
【分析】根据分式的分母不为零求解即可.
【解答】解:要使分式有意义,只须x﹣1≠0,即x≠1,
故选:D.
2.(2024秋 锦江区校级期末)下列不等式变形正确的是( )
A.由a>b,得am>bm
B.由a>b,得a﹣2024<b﹣2024
C.由ab>ac,得b<c
D.由,得b>c
【答案】D
【分析】不等式的基本性质:(1)等式的两边同时加上或减去同一个数或字母,不等号方向不变;(2)等式的两边同时乘以或除以同一个正数,不等号方向不变;(3)等式的两边同时乘以或除以同一个负数,不等号方向改变.据此逐项分析判断即可.
【解答】解:根据不等式的基本性质逐项分析判断如下:
A.由a>b,若m>0,则可得am>bm,故本选项变形错误,不符合题意;
B.由a>b,得a﹣2024>b﹣2024,故本选项变形错误,不符合题意;
C.由ab>ac,若a<0,则可得b<c,故本选项变形错误,不符合题意;
D. ,因为a2+1>0,所以可得b>c,故本选项变形正确,符合题意.
故选:D.
3.(2024秋 凤阳县期末)如图,在△ABC中,ED是AB的垂直平分线,AD=3,△ACE的周长为9.5,则△ABC的周长为( )
A.10.5 B.12.5 C.14.5 D.15.5
【答案】D
【分析】先利用线段垂直平分线的性质可得:BD=AD=3,EA=EB,AB=2AD=6,然后利用等量代换和三角形的周长公式进行计算,即可解答.
【解答】解:∵ED是AB的垂直平分线,AD=3,
∴BD=AD=3,EA=EB,AB=2AD=6,
∵△ACE的周长为9.5
∴AC+AE+EC=9.5,
∴AC+BE+EC=9.5,
∴AC+BC=9.5,
∴△ABC的周长为AB+AC+BC=9.5+6=15.5,
故选:D.
4.(2024秋 西安期末)下列各式不能运用平方差公式进行因式分解的是( )
A.﹣a2+b2 B.﹣x2﹣y2 C.49x2﹣z2 D.16m2﹣25n2
【答案】B
【分析】根据平方差公式的公式结构对各选项分析判断后利用排除法求解.
【解答】解:A、﹣a2+b2符合平方差公式结构,故本选项不合题意;
B、﹣x2﹣y2不符合平方差公式结构,故本选项符合题意;
C、49x2﹣z2符合平方差公式结构,故本选项不合题意;
D、16m2﹣25n2符合平方差公式结构,故本选项不合题意.
故选:B.
5.(2024秋 怀仁市期末)综合与实践活动小组的四位同学帮助某景区完成景区项目策划方案,需要解决下面的项目问题:如图,在该景区一块三角形绿地ABC的道路AB上建一个休息点M,使它到AC和BC两边的距离相等,在图中确定休息点M的位置.下列方案能满足项目要求的是( )
A. B.
C. D.
【答案】C
【分析】根据角平分线的性质、基本尺规作图判断即可.
【解答】解:∵点M到AC和BC两边的距离相等,且点M在AB上
∴点M是∠ACB的平分线与AB的交点,
∴C选项中的方案能满足项目要求,
故选:C.
6.(2024春 孝感期末)若关于x的不等式组的整数解有且只有3个,则m的取值范围为( )
A.m≥﹣1 B.m<1 C.0≤m<1 D.0<m≤1
【答案】C
【分析】根据解一元一次不等式组的步骤,表示出不等式组的解集,再根据整数解有且只有3个,得出关于m的不等式组即可解决问题.
【解答】解:解不等式x﹣m>0得,
x>m,
解不等式2x﹣3≥3(x﹣2)得,
x≤3,
因为不等式组的整数解有且只有3个,
所以0≤m<1.
故选:C.
7.(2024秋 任城区期末)如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为( )cm2
A.6 B.9 C.18 D.24
【答案】C
【分析】根据平移的性质求出空白部分的长和宽,根据矩形的面积公式计算,得到答案.
【解答】解:由平移的性质可知,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
则阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故选:C.
8.(2024秋 香河县期末)如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
【答案】B
【分析】根据分式的基本性质,进行作答,即可求解;
【解答】解:根据分式的基本性质可得:
,
分子扩大为原来的4倍,分母扩大为原来的2倍,因此分式的值整体扩大2倍;
故选:B.
9.(2024秋 临淄区期末)如图4×4的正方形网格中,其中一个三角形①绕某点旋转一定的角度,得到三角形②,则其旋转中心是( )
A.点A B.点B C.点C D.点D
【答案】B
【分析】根据旋转的性质,找出两组对应顶点的连线的垂直平分线,交点即为旋转中心.
【解答】解:如图:作出三角形①和三角形②两组对应点所连线段的垂直平分线的交点B为旋转中心.
故选:B.
10.(2024秋 孝昌县期末)已知x2﹣3x+2=0,则( )
A.1 B.2 C.3 D.4
【答案】C
【分析】将x2﹣3x+2=0两边分别除以x,进行求解即可.
【解答】解:∵x≠0,
∴,
∴,
∴;
故选:C.
11.(2024秋 青山湖区校级期末)▲若分式方程有增根,则m的值为( )
A.2 B.4 C.2或﹣2 D.4或﹣8
【答案】D
【分析】先根据解分式方程的方法求得m=3x﹣2,然后再根据分式方程有增根,可得x2﹣4=0,解得x=±2,把x的值代入3x﹣2进行计算即可.
【解答】解:去分母,得:m﹣2(x﹣2)=x+2,
去括号,得:m﹣2x+4=x+2,
移项、合并同类项,得:m=3x﹣2,
∵分式方程有增根,
∴x2﹣4=0,
∴x=±2,
当x=2时,m=3×2﹣2=4;
当x=﹣2时,m=3×(﹣2)﹣2=﹣8,
∴m的值可能为4或﹣8.
故选:D.
12.(2024秋 福山区期末)如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
【答案】A
【分析】根据三角形中位线定理得到△A1B1C1的周长a,△A2B2C2的周长aa,总结规律,根据规律解答即可.
【解答】解:∵点A1、B1、C1分别为BC、AC、AB的中点,
∴B1C1BC,A1C1AC,A1B1AB,
∴△A1B1C1的周长a,
同理,△A2B2C2的周长aa,
……
则△AnBn n的周长a,
故选:A.
二.填空题
13.(2022秋 渌口区期末)若分式的值为0,则x的值为 ﹣4 .
【答案】﹣4.
【分析】分式的值为零时,分子等于零,分母不等于零.
【解答】解:依题意,得:
|x|﹣4=0且x﹣4≠0,
解得x=﹣4.
故答案为:﹣4.
14.(2024春 五华县期末)如果多边形的每个外角都是30°,那么这个多边形的边数是 12 .
【答案】见试题解答内容
【分析】根据多边形的外角和是360度即可求得外角的个数,即多边形的边数.
【解答】解:多边形的边数是:360°÷30°=12.
故答案为:12.
15.(2021春 中牟县期末)如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为 100 cm.
【答案】见试题解答内容
【分析】判断出OC是△ABD的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得AD=2OC.
【解答】解:如图,过点A作AD⊥MN于点D,则AD∥OC.
∵O是AB的中点,
∴OC是△ABD的中位线,
∴AD=2OC=2×50=100(cm).
故答案为:100.
16.(2024秋 醴陵市期末)若关于x的方程的解为正数,则m的取值范围是 m<3且m≠2 .
【答案】m<3且m≠2.
【分析】先解关于x的分式方程,它的解x用含量m的代数式表示,再根据“原分式方程有解”和“方程的解是正数”建立关于m的不等式,求解即可.
【解答】解:,
解得:x=3﹣m,
∵原分式方程有解,
∴x﹣1≠0,即3﹣m≠1(求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值,这个值叫方程的解),
解得:m≠2,
∵方程的解是正数,
∴3﹣m>0,
解得:m<3,
∴m<3且m≠2,
故答案为:m<3且m≠2.
17.(2024秋 章丘区期末)如图,E,F分别是平行四边形ABCD的边AD,BC上的点,AF与BE相交于点P,DF与CE相交于点Q,若,则阴影部分四边形EPFQ的面积为 27 cm2.
【答案】27.
【分析】连接EF,由三角形的面积公式我们可以推出S△EFC=S△DCF,S△BFE=S△BFA所以S△EFQ=S△DCQ,S△EFP=S△ABP,因此可以推出阴影部分的面积就是S四边形EPFQ=S△ABP+S△DCQ,解答此题关键是作出辅助线,找出同底等高的三角形.
【解答】解:如图,连接EF,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△DCF的FC边上的高相等,
∴S△EFC=S△DCF,
∴S△EFQ=S△DCQ,
同理S△BFE=S△BFA,
∴S△EFP=S△ABP,
∵,,
∴,
故答案为:27.
18.(2025春 昆明期中)已知直角坐标系内有四个点A(0,0),B(5,0),C(2,3),D(x,y),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为: (3,﹣3)或(﹣3,3)或(7,3) .
【答案】(3,﹣3)或(﹣3,3)或(7,3).
【分析】由平行四边形的性质和中点坐标公式可求解.
【解答】解:①当AB为对角线时,中点坐标为(,),即(,0),
根据平行四边形的性质,得,0,
解得x=3,y=﹣3,
∴点D的坐标为(3,﹣3);
②当AC为对角线时,中点坐标为(,),即(1,),
根据平行四边形的性质,得1,
解得x=﹣3,y=3,
∴点D的坐标为(﹣3,3);
③当BC为对角线时,中点坐标为(,),即(,),
根据平行四边形的性质,得,
解得x=7,y=3,
∴点D的坐标为(7,3);
故答案为:(3,﹣3)或(﹣3,3)或(7,3).
三.解答题
19.(2024秋 内乡县期末)分解因式:
(1)﹣9x3y+6x2y2﹣xy3;
(2)m2(a﹣b)+n2(b﹣a).
【答案】(1)﹣xy(3x﹣y)2;
(2)(a﹣b)(m+n)(m﹣n).
【分析】(1)先提公因式,再利用完全平方公式分解因式即可;
(2)先变形,再提公因式,然后利用平方差公式分解因式即可.
【解答】解:(1)﹣9x3y+6x2y2﹣xy3
=﹣xy(9x2﹣6xy+y2)
=﹣xy(3x﹣y)2;
(2)m2(a﹣b)+n2(b﹣a)
=m2(a﹣b)﹣n2(a﹣b)
=(a﹣b)(m2﹣n2)
=(a﹣b)(m+n)(m﹣n).
20.(2021秋 石泉县期末)解分式方程:2.
【答案】见试题解答内容
【分析】先把分式方程变成整式方程,求出方程的解,最后进行检验即可.
【解答】解:方程两边都乘以2(x﹣1)得:2x=3﹣4(x﹣2),
解得:x,
检验:把x代入2(x﹣1)≠0,
所以x是原方程的解,
所以原方程的解为x.
21.(2024秋 平邑县期末)阅读材料,拓展知识.
第一步:要把多项式am+an+bm+bn分解因式,可以先把它的前两项分成一组,并提出公因式a,再把它的后两项分成一组,提出公因式b,从而可得:am+an+bn+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b),这种方法称为分组法.
第二步:理解知识,尝试填空.
(1)ab﹣ac+bc﹣b2=(ab﹣ac)+(bc﹣b2)=a(b﹣c)+b(c﹣b)= (b﹣c)(a﹣b) .
第三步:应用知识,解决问题.
(2)因式分解:
①m2+5n﹣mn﹣5m= (m﹣n)(m﹣5) .
②x2﹣2x+1﹣y2= (x﹣1+y)(x﹣1﹣y) .
第四步:提炼思想,拓展应用.
(3)已知三角形的三边长分别是a、b、c,且满足a2+2b2+c2=2b(a+c),试判断这个三角形的形状,并说明理由.
【答案】(1)(b﹣c)(a﹣b);
(2)①(m﹣n)(m﹣5);②(x﹣1+y)(x﹣1﹣y);
(3)这个三角形为等边三角形,理由见解析.
【分析】(1)仿照例题,先分组,再利用提取公因式法分解即可;
(2)①先分组,用提取公因式法分解,再用平方差公式分解即可;
②先分组,用提取公因式法分解,再用平方差公式分解即可;
(3)移项后分解因式,可得出a=b=c,则可得出答案.
【解答】解:(1)ab﹣ac+bc﹣b2
=(ab﹣ac)+(bc﹣b2)
=a(b﹣c)﹣b(b﹣c)
=(b﹣c)(a﹣b),
故答案为:(b﹣c)(a﹣b);
(2)①m2+5n﹣mn﹣5m
=m2﹣mn+5n﹣5m
=m(m﹣n)+5(n﹣m)
=m(m﹣n)﹣5(m﹣n)
=(m﹣n)(m﹣5);
②x2﹣2x+1﹣y2
=(x2﹣2x+1)﹣y2
=(x﹣1)2﹣y2
=(x﹣1+y)(x﹣1﹣y);
(3)这个三角形为等边三角形.
理由如下:
∵a2+2b2+c2=2b(a+c),
∴a2+2b2+c2﹣2ba﹣2bc=0,
∴a2﹣2ba+b2+c2﹣2bc+b2=0,
∴(a﹣b)2+(b﹣c)2=0,
∵(a﹣b)2≥0,(b﹣c)2≥0,
∴a﹣b=0,b﹣c=0,
∴a=b=c,
∴这个三角形是等边三角形.
22.(2025 龙凤区校级三模)先化简,再求值:,其中.
【答案】,.
【分析】先通分括号内的式子,同时将除法转化为乘法,再约分,然后将a的值代入化简后的式子计算即可.
【解答】解:
,
当a1时,原式.
23.(2025 镇江模拟)如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)若AE=CE,BC=2AB,BC=6,求四边形AECF的面积.
【答案】见试题解答内容
【分析】(1)根据平行四边形的性质得出AB=CD,BC=AD,∠B=∠D,求出BE=DF,根据全等三角形的判定推出即可;
(2)求出△ABE是等边三角形,求出高AH的长,再求出面积即可.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠D,
∵点E、F分别是BC、AD的中点,
∴BEBC,DFAD,
∴BE=DF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS);
(2)解:作AH⊥BC于H,
∵BC=2AB=6,E为BC中点,F为AD的中点,
∴AB=BE=CE=AF=DF=3,
∴四边形AECF是平行四边形,
∵AE=EC,
∴AE=AB=BE=CE=3,
∴△ABE是等边三角形,
∴∠B=60°,
∴AH=AB×sin60°=3,
∴四边形AECF的面积是CE×AH=3.
24.(2025 成都)2025年8月7日至17日,第12届世界运动会将在成都举行,与运动会吉祥物“蜀宝”“锦仔”相关的文创产品深受大家喜爱.某文旅中心在售A,B两种吉祥物挂件,已知每个B种挂件的价格是每个A种挂件价格的,用300元购买B种挂件的数量比用200元购买A种挂件的数量多7个.
(1)求每个A种挂件的价格;
(2)某游客计划用不超过600元购买A,B两种挂件,且购买B种挂件的数量比A种挂件的数量多5个,求该游客最多购买多少个A种挂件.
【答案】(1)每个A种挂件的价格为25元;(2)该游客最多购买11个A种挂件.
【分析】(1)依据题意,设每个A种挂件的价格为x元,则每个B种挂件的价格为x元,可得7,求出x后即可判断得解;
(2)依据题意,设该游客最多购买m个A种挂件,则购买(m+5)个B种挂件,又结合(1)每个A种挂件的价格为25元,每个B种挂件的价格为25=20元,可得25m+20(m+5)≤600,进而计算可以判断得解.
【解答】解:(1)由题意,设每个A种挂件的价格为x元,
则每个B种挂件的价格为x元,
∴7.
∴x=25.
经检验:x=25是原方程的根.
答:每个A种挂件的价格为25元.
(2)由题意,设该游客最多购买m个A种挂件,
则购买(m+5)个B种挂件,
又结合(1)每个A种挂件的价格为25元,每个B种挂件的价格为25=20元,
∴25m+20(m+5)≤600.
∴m11.
又∵m为整数,
∴m=11,则该游客最多购买11个A种挂件.
25.(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
【答案】(1)证明见解答过程;
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
【分析】(1)根据小明的作法知,CF=AE,根据平行四边形的性质求出AD∥BC,根据“一组对边平行且相等的四边形是平行四边形”求出四边形AFCE是平行四边形,根据“平行四边形的对边互相平行”即可得证;
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
【解答】(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE;
(2)解:以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
第1页(共1页)
同课章节目录
