人教版六年级下册数学期末专项训练:选择题(含解析)
文档属性
| 名称 | 人教版六年级下册数学期末专项训练:选择题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 20:07:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版六年级下册数学期末专项训练:填空题
一、选择题
1.一个点,从直线上的0处出发,先向右移动4个单位,再向左移动7个单位,这时这个点所对的数是( )。
A. B. C.
2.做一个无盖的圆柱形水桶,需要铁皮的面积是( )。
A.侧面积+底面积 B.侧面积+底面积×2
C.侧面积×2+底面积
3.能与0.3∶4组成比例的是( )。
A.4∶0.3 B.3∶40 C.3∶4
4.如果用﹢3米表示高出警戒水位3米,那么低于警戒水位5米记作( )。
A.﹢5米 B.﹣5米 C.0米 D.﹣10米
5.纸片上分别写着2、6、5、8,任抽一张抽到偶数的可能性是( ).
A. B. C.
6.制作一个圆柱形的无盖铁桶需要多大的铁皮,其实是求这个圆柱形的( )。
A.表面积 B.体积 C.侧面积 D.侧面积+1个底面积
7.下图是王亮某天的微信账单,“﹣77.23”表示( )。
A.支出77.23元 B.收入77.23元 C.负77.23元
8.张阿姨把50000元存入银行,存期为3年,年利率为2.75%,到期后张阿姨可以得到多少利息?正确的列式是( )。
A.50000×2.75%×3+50000 B.50000×2.75%+50000 C.50000×2.75%×3 D.50000×2.75%
9.读作( )。
A.九分之五 B.负九分之五 C.负五分之九
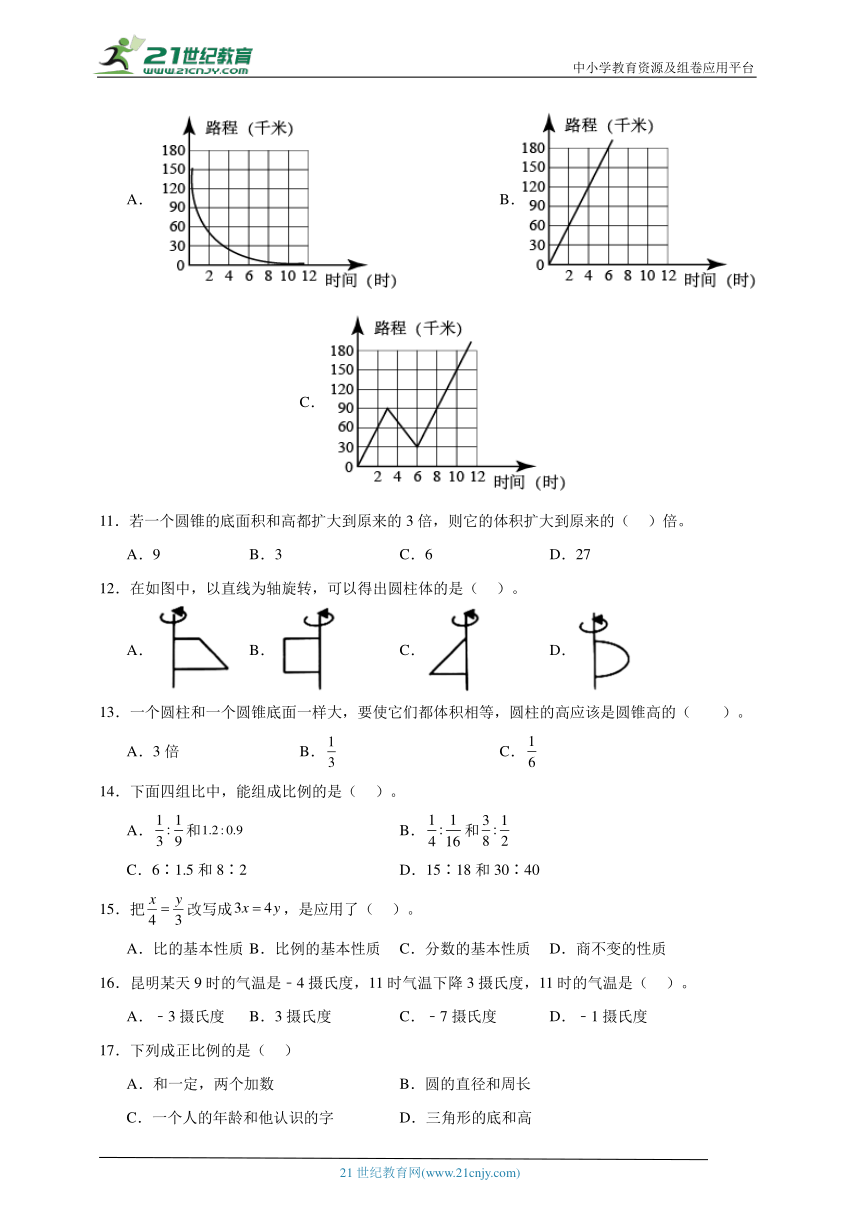
10.下列各图中,能表示出两个量成正比例关系的是( )。
A. B. C.
11.若一个圆锥的底面积和高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A.9 B.3 C.6 D.27
12.在如图中,以直线为轴旋转,可以得出圆柱体的是( )。
A. B. C. D.
13.一个圆柱和一个圆锥底面一样大,要使它们都体积相等,圆柱的高应该是圆锥高的( )。
A.3倍 B. C.
14.下面四组比中,能组成比例的是( )。
A.和 B.和
C.6∶1.5和8∶2 D.15∶18和30∶40
15.把改写成,是应用了( )。
A.比的基本性质 B.比例的基本性质 C.分数的基本性质 D.商不变的性质
16.昆明某天9时的气温是﹣4摄氏度,11时气温下降3摄氏度,11时的气温是( )。
A.﹣3摄氏度 B.3摄氏度 C.﹣7摄氏度 D.﹣1摄氏度
17.下列成正比例的是( )
A.和一定,两个加数 B.圆的直径和周长
C.一个人的年龄和他认识的字 D.三角形的底和高
18.一根木料锯成5段要用16分钟,照这样计算,把这根木料锯成10段要用多长时间?如果设需要用的时间为x分钟,列式正确的是( )。
A.= B.= C.= D.=
19.一个底面周长是125.6厘米的圆柱形容器中盛有水,水面的高度是20厘米。将一块石头浸没在容器中的水里后,水面的高度是23厘米,如图。这块石头的体积是( )立方厘米。
A.376.8 B.15072 C.3768
20.观察如图的示意图,图中各场所的方位描述正确的是( )。
A.医院在学校北偏西20°方向100m处
B.邮局在学校西偏南20°方向300m处
C.公园在学校北偏东45°方向100m处
D.学校在广场南偏东45°方向100m处
21.若圆柱的侧面积沿高展开后是一个正方形,则底面直径与高的比是( )。
A.1:1 B.:1 C.1:
22.0不是正数,也不是负数,它比所有的( )大.
A.正数 B.负数 C.小数
23.一个圆柱和一个圆锥体积相等,已知圆锥体和圆柱的高的比是9:1,圆柱体底面积和圆锥体底面积的比是( )
A.9:1 B.3:1 C.6:1
24.下列叙述中,正确的有( )个。
(1)若a∶b=c∶d,则b∶d=a∶c
(2)把一个长方形按2∶1放大后,它的面积也按2∶1放大。
(3)如果一个圆柱的体积是圆锥的3倍,那么它们一定等底等高。
(4)分数的分子和分母同时乘或除以相同的数,分数的大小不变。
A.1 B.2 C.3 D.4
25.一个圆柱的半径扩大3倍,高缩小3倍,体积( )
A.扩大3倍 B.扩大9倍 C.扩大27倍 D.不变
26.李伟将2000元存人银行,存期三年,年利率是2.75%。到期后,李伟一共可以取出( )元。
A.55 B.165 C.2055 D.2165
27.2018年1月13日,天水的气温是﹣3℃~8℃,则这天的温差是( )。
A.5℃ B.11℃ C.3℃ D.8℃
28.两张同样大小的长方形纸,分别围成一个最大的圆柱,则它们的侧面积( )。
A.一定相等 B.一定不相等 C.不一定相等 D.无法确定
29.两张中国地图。甲图的比例尺是,乙图的比例尺是,甲图上北京到上海的图距是乙图上这两地之间图距的( )。
A. B. C. D.
30.一个圆锥与一个圆柱的体积比是1:2,底面积之比是3:4,圆柱的高是9厘米.圆锥的高是( )厘米.
A.36 B.6 C.9 D.18
《人教版六年级下册数学期末专项训练:填空题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B C D A C B B
题号 11 12 13 14 15 16 17 18 19 20
答案 A B B C B C B C C C
题号 21 22 23 24 25 26 27 28 29 30
答案 C B B A A D B A B D
1.C
【分析】先画出一条标有正负数的直线,这个点从0开始,先向右移动4个单位,到﹢4处,再从﹢4开始,向左移动7个单位,到﹣3处,如图所示,据此即可选择。
【详解】由分析可知,这个点从0处出发,先向右移动4个单位,再向左移动7个单位,这时这个点所对的数是﹣3;
故答案为:C
2.A
【分析】圆柱的表面积包括侧面积和两个底面积,而无盖的圆柱形水桶没有上底面,所以求铁皮的面积就是求圆柱的侧面积与1个底面积之和。
【详解】做一个无盖的圆柱形水桶,需要铁皮的面积是侧面积+底面积。
故答案为:A
【点睛】本题考查对圆柱表面积的认识,理解圆柱形的无盖水桶是一个少了上底面的圆柱体。
3.B
【分析】根据题意,先将0.3∶4化简比,根据化简小数比的方法:比的前项和后项同时扩大相同的倍数,成为整数,如果不是最简比,再同时除以相同的数,据此解答。
【详解】求比值和化简比
0.3∶ 4=(0.3×10)∶(4×10)= 3∶40
故答案为:B
4.B
【分析】如果高出警戒水位记为正,那么低于警戒水位记为负,据此分析。
【详解】如果用﹢3米表示高出警戒水位3米,那么低于警戒水位5米记作﹣5米。
故答案为:B
【点睛】关键是理解正负数的意义,正负数可以表示相反意义的量。
5.C
【详解】略
6.D
【分析】求制作一个圆柱形的无盖铁桶需要多大的铁皮,就是求铁皮的面积;圆柱的表面积包括侧面积和两个底面积,而圆柱形无盖铁桶没有上底面,所以求铁皮的面积就是求圆柱的侧面积和1个底面积之和。
【详解】制作一个圆柱形的无盖铁桶需要多大的铁皮,其实是求这个圆柱形的侧面积+1个底面积。
故答案为:D
【点睛】本题考查对圆柱的侧面积、表面积、体积概念的认识,理解圆柱形的无盖铁桶是一个少了上底面的圆柱体。
7.A
【分析】正数、负数表示两种相反意义的量。如果规定微信收到的红包记作正,那么支出就记作负,据此解答。
【详解】王亮某天的微信账单,“﹣77.23”表示支出77.23元。
故答案为:A
8.C
【分析】根据利息的计算方法可得:利息=本金×利率×存期,本题中50000元是本金,存期为3年,年利率为2.75%,代入到公式中即可得解。
【详解】50000×2.75%×3
=1375×3
=4125(元)
故答案为:C
【点睛】此题主要考查利息的计算方法,直接根据利息公式求解。
9.B
【分析】负数的读法是:先读“负”,再读数,读分数时,先读分母,再读分子,据此分析。
【详解】读作负九分之五。
故答案为:B
10.B
【分析】根据正比例和反比例的图像的特点,正比例图像是一条直线,反比例图像是一条平滑的曲线。据此解答。
【详解】A.图像是一条平滑的曲线,所以路程与时间成反比例关系。
B.图像是一条直线,所以路程与时间成正比例关系。
C.图像是一条折线,所以路程与时间不成比例。
故答案为:B
【点睛】本题考查了正比例和反比例的图像,需熟记图像的特点及反映出的比例关系。
11.A
【分析】根据圆锥的体积公式V锥=Sh,以及积的变化规律:因数乘几或除以几(0除外),积也乘几或除以几;可知圆锥的底面积和高都扩大到原来的3倍,则它的体积扩大到原来的(3×3)倍。
【详解】3×3=9
若一个圆锥的底面积和高都扩大到原来的3倍,则它的体积扩大到原来的9倍。
故答案为:A
【点睛】掌握圆锥的体积计算公式以及积的变化规律是解题的关键。
12.B
【分析】以长方形或正方形的一边所在的直线为轴旋转一周,由于长方形或正方形的特点,它的上、下两个面是以长方形或正方形的另一条边为半径的两个完全一样的圆,与轴平行的一边通过旋转形成一个曲面,这样就得到一个圆柱。
【详解】
A.直角梯形以直线为轴旋转,可以得出圆台;
B.正方形以直线为轴旋转,可以得出圆柱体;
C.直角三角形以直线为轴旋转,可以得出圆锥体;
D.半圆以直线为轴旋转,可以得出球体。
故答案为:B
13.B
【分析】根据等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍解答即可。
【详解】一个圆柱和一个圆锥底面积和体积都相等,那么圆柱的高应该是圆锥高的。
故答案为:B
14.C
【分析】表示两个比相等的式子叫做比例,据此可先逐项求出每个比的比值,再根据两个比的比值相等,就能组成比例,比值不相等,就不能组成比例。
【详解】A.,,,所以和不能组成比例;
B.,,,所以和不能组成比例;
C.6∶1.5=6÷1.5=4,8∶2=8÷2=4,4=4,所以6∶1.5和8∶2能组成比例;
D.15∶18=15÷18=,30∶40=30÷40=,≠,所以15∶18和30∶40不能组成比例。
故答案为:C
【点睛】解决此题关键根据比例的意义,先求出每个比的比值,进而根据比值相等,就能组成比例得解。
15.B
【分析】在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质,据此解答。
【详解】由分析可知,把改写成,是应用了比例的基本性质。
故选择:B。
【点睛】如果把比例写成分数形式,等号两边的分子和分母分别交叉相乘,所得的积相等。
16.C
【分析】由题意可知,11时的气温=9时的气温-11时比9时下降的气温,求出9时去掉负号后的气温与下降气温的和,最后再加上负号即可。
【详解】4+3=7(摄氏度)
所以,11时的气温是﹣7摄氏度。
故答案为:C
【点睛】本题主要考查正负数的简单计算,掌握负数减负数的计算方法是解答题目的关键。
17.B
【分析】根据判断两种量成正比例还是成反比例的方法:关键是看这两种相关联的量中相对应的两个数的商一定还是积一定,如果商一定,就成正比例关系;如果积一定,就成反比例关系;据此对各题进行依次分析,进而得出结论。
【详解】A、和一定,两个加数不成比例;
B、因为圆的周长÷直径=π(一定),所以圆的周长和直径成正比例,符合题意;
C、一个人的年龄和他认识的字不成比例;
D、当三角形的面积一定时,三角形的底与高成反比例。
【点睛】此题考查了判断两种量成正比例还是成反比例的方法。
18.C
【分析】由题意可知,一根木料锯成5段,则需要锯5-1=4次,则锯成10段需要锯10-1=9次,锯一次所需要的时间是相同的,则锯木料用的时间与锯的次数成正比例,据此列比例解答即可。
【详解】=
解:4=
x=4×9
x=36
故答案为:C
【点睛】本题考查用比例解决实际问题,明确锯木料用的时间与锯的次数成正比例是解题的关键。
19.C
【分析】已知物体的体积=上升部分水的体积,物体的体积=底面积×上升部分的高度,根据圆柱的体积公式,用底面积×上升部分的高度即可求出石头的体积,据此解答。
【详解】125.6÷3.14÷2
=40÷2
=20(厘米)
3.14×202×(23-20)
=3.14×400×3
=1256×3
=3768(立方厘米)
这块石头的体积是3768立方厘米。
故答案为:C
20.C
【分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是学校。根据图上距离和比例尺的关系确定实际距离。
【详解】A.50×2=100(米)
医院在学校西偏北20°方向100m处。所以原说法错误。
B.50×3=150(米)
邮局在学校西偏南20°方向150m处。所以原说法错误。
C.50×2=100(米)
公园在学校北偏东45°方向100m处。所以原说法正确。
D.50×2=100(米)
广场在学校南偏东45°方向100m处,则学校在广场北偏西45°方向100m处。所以原说法错误。
故答案为:C
【点睛】本题主要考查图上距离、实际距离与比例尺之间的关系,并会根据物体的位置描述方向。
21.C
【解析】略
22.B
【详解】根据正、负数的意义,可得0不是正数,也不是负数;然后根据正数>0>负数,可得0比所有的负数大,据此解答即可.
23.B
【分析】根据圆柱的体积公式V=sh,与圆锥的体积公式V=sh,知道当圆柱与圆锥的体积相等时,底面积的比和高的比是成反比的关系,由此即可解答.
【详解】因为,圆锥体和圆柱的高的比是:9:1,
圆柱的体积公式是:V=sh,
圆锥的体积公式是:V=sh,
所以,圆锥体和圆柱的底面积的比是:1:3,
即圆柱体底面积和圆锥体底面积的比是:3:1,
24.A
【分析】根据比例的性质、图形的放大、圆柱和圆锥的体积关系以及分数的基本性质,一一判断各叙述的正误,再选出正确选项即可。
【详解】(1)根据比例的性质,比例的两内项和两外项同时变更位置,比例仍然成立。所以,原说法正确;
(2)长方形按2∶1放大后,长和宽都扩大到原来的2倍,此时面积扩大到原来的4倍。所以,原说法错误;
(3)如果一个圆柱的体积是圆锥的3倍,它们的底和高不一定存在关系。所以,原说法错误;
(4)分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。所以,原说法错误。
所以,只有一个叙述是正确的。
故答案为:A
【点睛】本题考查了比例的性质、图形的放大、圆柱和圆锥的体积关系以及分数的基本性质,明确各个性质和概念是解题的关键。
25.A
【详解】试题分析:根据题意,可设圆柱的半径为r,高为h,根据圆柱的体积=底面积×高计算出圆柱原来的体积与改变后的体积,然后再用改变后的体积除以原来的体积即可得到答案。
解:可设圆柱的半径为r,高为h
圆柱原来的体积为:πr2h
改变后的圆柱的体积为:9πr2×h=3πr2h
体积扩大了:3πr2h÷πr2h=3
即一个圆柱的半径扩大3倍,高缩小3倍,体积就会扩大3倍。
故选A。
点评:此题主要考查的是圆柱的体积公式及其灵活应用。
26.D
【分析】利息=本金×年利率×时间,由此代入数据求出利息,再加上本金即可解答。
【详解】2000×2.75%×3+2000
=2000×0.0275×3+2000
=165+2000
=2165(元)
到期后,李伟一共可以取出2165元。
故答案为:D
【点睛】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×时间(注意时间和利率的对应)。
27.B
【分析】正数、负数表示两种相反意义的量;比0℃低的温度叫零下温度,通常在数字前面加“﹣”(负号);比0℃高的温度叫零上温度,通常在数字前面加“﹢”(正号),也可以省略不写。
﹣3℃与0℃相差3℃,8℃与0℃相差8℃,所以最低气温与最高气温的温差是(3+8)℃。
【详解】3+8=11℃
故答案为:B
【点睛】掌握正负数的意义以及温差的计算方法。
28.A
【分析】用长方形的纸围成一个最大的圆柱,圆柱的侧面积等于这张纸的面积,因为这两张纸的大小一样,所以这两个长方形的面积相等,即圆柱的侧面积相等,据此解答。
【详解】分析可知,两张同样大小的长方形纸,分别围成一个最大的圆柱,圆柱的侧面积都等于长方形的面积,所以这两个圆柱的侧面积一定相等。
故答案为:A
【点睛】本题主要考查圆柱的侧面积,理解圆柱的侧面积等于长方形的面积是解答题目的关键。
29.B
【分析】图上距离∶实际距离=比例尺,因为实际距离不变,所以图上距离与实际距离成正比,则甲图上北京到上海的图距是乙图上这两地之间图距的几分之几,用甲图的比例尺除以乙图的比例尺即可。
【详解】
故答案为:B
30.D
【详解】试题分析:设圆锥的体积为V,底面积为S,则圆柱的体积是2V,底面积是S,利用圆柱和圆锥的体积公式推导出它们高的比是几比几,即可解答.
解:设圆锥的体积为V,底面积为S,则圆柱的体积是2V,底面积是S,
则圆锥的高为:,
圆柱的高为:=,
则圆锥的高与圆柱的高的比是::=2:1,
因为圆柱的高是9厘米,
所以圆锥的高是:9×2=18(厘米),
答:圆柱的高是18厘米.
故选D.
点评:此题主要考查了圆柱和圆锥的体积公式的灵活应用,利用公式推导出它们高的比是解决此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级下册数学期末专项训练:填空题
一、选择题
1.一个点,从直线上的0处出发,先向右移动4个单位,再向左移动7个单位,这时这个点所对的数是( )。
A. B. C.
2.做一个无盖的圆柱形水桶,需要铁皮的面积是( )。
A.侧面积+底面积 B.侧面积+底面积×2
C.侧面积×2+底面积
3.能与0.3∶4组成比例的是( )。
A.4∶0.3 B.3∶40 C.3∶4
4.如果用﹢3米表示高出警戒水位3米,那么低于警戒水位5米记作( )。
A.﹢5米 B.﹣5米 C.0米 D.﹣10米
5.纸片上分别写着2、6、5、8,任抽一张抽到偶数的可能性是( ).
A. B. C.
6.制作一个圆柱形的无盖铁桶需要多大的铁皮,其实是求这个圆柱形的( )。
A.表面积 B.体积 C.侧面积 D.侧面积+1个底面积
7.下图是王亮某天的微信账单,“﹣77.23”表示( )。
A.支出77.23元 B.收入77.23元 C.负77.23元
8.张阿姨把50000元存入银行,存期为3年,年利率为2.75%,到期后张阿姨可以得到多少利息?正确的列式是( )。
A.50000×2.75%×3+50000 B.50000×2.75%+50000 C.50000×2.75%×3 D.50000×2.75%
9.读作( )。
A.九分之五 B.负九分之五 C.负五分之九
10.下列各图中,能表示出两个量成正比例关系的是( )。
A. B. C.
11.若一个圆锥的底面积和高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A.9 B.3 C.6 D.27
12.在如图中,以直线为轴旋转,可以得出圆柱体的是( )。
A. B. C. D.
13.一个圆柱和一个圆锥底面一样大,要使它们都体积相等,圆柱的高应该是圆锥高的( )。
A.3倍 B. C.
14.下面四组比中,能组成比例的是( )。
A.和 B.和
C.6∶1.5和8∶2 D.15∶18和30∶40
15.把改写成,是应用了( )。
A.比的基本性质 B.比例的基本性质 C.分数的基本性质 D.商不变的性质
16.昆明某天9时的气温是﹣4摄氏度,11时气温下降3摄氏度,11时的气温是( )。
A.﹣3摄氏度 B.3摄氏度 C.﹣7摄氏度 D.﹣1摄氏度
17.下列成正比例的是( )
A.和一定,两个加数 B.圆的直径和周长
C.一个人的年龄和他认识的字 D.三角形的底和高
18.一根木料锯成5段要用16分钟,照这样计算,把这根木料锯成10段要用多长时间?如果设需要用的时间为x分钟,列式正确的是( )。
A.= B.= C.= D.=
19.一个底面周长是125.6厘米的圆柱形容器中盛有水,水面的高度是20厘米。将一块石头浸没在容器中的水里后,水面的高度是23厘米,如图。这块石头的体积是( )立方厘米。
A.376.8 B.15072 C.3768
20.观察如图的示意图,图中各场所的方位描述正确的是( )。
A.医院在学校北偏西20°方向100m处
B.邮局在学校西偏南20°方向300m处
C.公园在学校北偏东45°方向100m处
D.学校在广场南偏东45°方向100m处
21.若圆柱的侧面积沿高展开后是一个正方形,则底面直径与高的比是( )。
A.1:1 B.:1 C.1:
22.0不是正数,也不是负数,它比所有的( )大.
A.正数 B.负数 C.小数
23.一个圆柱和一个圆锥体积相等,已知圆锥体和圆柱的高的比是9:1,圆柱体底面积和圆锥体底面积的比是( )
A.9:1 B.3:1 C.6:1
24.下列叙述中,正确的有( )个。
(1)若a∶b=c∶d,则b∶d=a∶c
(2)把一个长方形按2∶1放大后,它的面积也按2∶1放大。
(3)如果一个圆柱的体积是圆锥的3倍,那么它们一定等底等高。
(4)分数的分子和分母同时乘或除以相同的数,分数的大小不变。
A.1 B.2 C.3 D.4
25.一个圆柱的半径扩大3倍,高缩小3倍,体积( )
A.扩大3倍 B.扩大9倍 C.扩大27倍 D.不变
26.李伟将2000元存人银行,存期三年,年利率是2.75%。到期后,李伟一共可以取出( )元。
A.55 B.165 C.2055 D.2165
27.2018年1月13日,天水的气温是﹣3℃~8℃,则这天的温差是( )。
A.5℃ B.11℃ C.3℃ D.8℃
28.两张同样大小的长方形纸,分别围成一个最大的圆柱,则它们的侧面积( )。
A.一定相等 B.一定不相等 C.不一定相等 D.无法确定
29.两张中国地图。甲图的比例尺是,乙图的比例尺是,甲图上北京到上海的图距是乙图上这两地之间图距的( )。
A. B. C. D.
30.一个圆锥与一个圆柱的体积比是1:2,底面积之比是3:4,圆柱的高是9厘米.圆锥的高是( )厘米.
A.36 B.6 C.9 D.18
《人教版六年级下册数学期末专项训练:填空题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B C D A C B B
题号 11 12 13 14 15 16 17 18 19 20
答案 A B B C B C B C C C
题号 21 22 23 24 25 26 27 28 29 30
答案 C B B A A D B A B D
1.C
【分析】先画出一条标有正负数的直线,这个点从0开始,先向右移动4个单位,到﹢4处,再从﹢4开始,向左移动7个单位,到﹣3处,如图所示,据此即可选择。
【详解】由分析可知,这个点从0处出发,先向右移动4个单位,再向左移动7个单位,这时这个点所对的数是﹣3;
故答案为:C
2.A
【分析】圆柱的表面积包括侧面积和两个底面积,而无盖的圆柱形水桶没有上底面,所以求铁皮的面积就是求圆柱的侧面积与1个底面积之和。
【详解】做一个无盖的圆柱形水桶,需要铁皮的面积是侧面积+底面积。
故答案为:A
【点睛】本题考查对圆柱表面积的认识,理解圆柱形的无盖水桶是一个少了上底面的圆柱体。
3.B
【分析】根据题意,先将0.3∶4化简比,根据化简小数比的方法:比的前项和后项同时扩大相同的倍数,成为整数,如果不是最简比,再同时除以相同的数,据此解答。
【详解】求比值和化简比
0.3∶ 4=(0.3×10)∶(4×10)= 3∶40
故答案为:B
4.B
【分析】如果高出警戒水位记为正,那么低于警戒水位记为负,据此分析。
【详解】如果用﹢3米表示高出警戒水位3米,那么低于警戒水位5米记作﹣5米。
故答案为:B
【点睛】关键是理解正负数的意义,正负数可以表示相反意义的量。
5.C
【详解】略
6.D
【分析】求制作一个圆柱形的无盖铁桶需要多大的铁皮,就是求铁皮的面积;圆柱的表面积包括侧面积和两个底面积,而圆柱形无盖铁桶没有上底面,所以求铁皮的面积就是求圆柱的侧面积和1个底面积之和。
【详解】制作一个圆柱形的无盖铁桶需要多大的铁皮,其实是求这个圆柱形的侧面积+1个底面积。
故答案为:D
【点睛】本题考查对圆柱的侧面积、表面积、体积概念的认识,理解圆柱形的无盖铁桶是一个少了上底面的圆柱体。
7.A
【分析】正数、负数表示两种相反意义的量。如果规定微信收到的红包记作正,那么支出就记作负,据此解答。
【详解】王亮某天的微信账单,“﹣77.23”表示支出77.23元。
故答案为:A
8.C
【分析】根据利息的计算方法可得:利息=本金×利率×存期,本题中50000元是本金,存期为3年,年利率为2.75%,代入到公式中即可得解。
【详解】50000×2.75%×3
=1375×3
=4125(元)
故答案为:C
【点睛】此题主要考查利息的计算方法,直接根据利息公式求解。
9.B
【分析】负数的读法是:先读“负”,再读数,读分数时,先读分母,再读分子,据此分析。
【详解】读作负九分之五。
故答案为:B
10.B
【分析】根据正比例和反比例的图像的特点,正比例图像是一条直线,反比例图像是一条平滑的曲线。据此解答。
【详解】A.图像是一条平滑的曲线,所以路程与时间成反比例关系。
B.图像是一条直线,所以路程与时间成正比例关系。
C.图像是一条折线,所以路程与时间不成比例。
故答案为:B
【点睛】本题考查了正比例和反比例的图像,需熟记图像的特点及反映出的比例关系。
11.A
【分析】根据圆锥的体积公式V锥=Sh,以及积的变化规律:因数乘几或除以几(0除外),积也乘几或除以几;可知圆锥的底面积和高都扩大到原来的3倍,则它的体积扩大到原来的(3×3)倍。
【详解】3×3=9
若一个圆锥的底面积和高都扩大到原来的3倍,则它的体积扩大到原来的9倍。
故答案为:A
【点睛】掌握圆锥的体积计算公式以及积的变化规律是解题的关键。
12.B
【分析】以长方形或正方形的一边所在的直线为轴旋转一周,由于长方形或正方形的特点,它的上、下两个面是以长方形或正方形的另一条边为半径的两个完全一样的圆,与轴平行的一边通过旋转形成一个曲面,这样就得到一个圆柱。
【详解】
A.直角梯形以直线为轴旋转,可以得出圆台;
B.正方形以直线为轴旋转,可以得出圆柱体;
C.直角三角形以直线为轴旋转,可以得出圆锥体;
D.半圆以直线为轴旋转,可以得出球体。
故答案为:B
13.B
【分析】根据等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍解答即可。
【详解】一个圆柱和一个圆锥底面积和体积都相等,那么圆柱的高应该是圆锥高的。
故答案为:B
14.C
【分析】表示两个比相等的式子叫做比例,据此可先逐项求出每个比的比值,再根据两个比的比值相等,就能组成比例,比值不相等,就不能组成比例。
【详解】A.,,,所以和不能组成比例;
B.,,,所以和不能组成比例;
C.6∶1.5=6÷1.5=4,8∶2=8÷2=4,4=4,所以6∶1.5和8∶2能组成比例;
D.15∶18=15÷18=,30∶40=30÷40=,≠,所以15∶18和30∶40不能组成比例。
故答案为:C
【点睛】解决此题关键根据比例的意义,先求出每个比的比值,进而根据比值相等,就能组成比例得解。
15.B
【分析】在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质,据此解答。
【详解】由分析可知,把改写成,是应用了比例的基本性质。
故选择:B。
【点睛】如果把比例写成分数形式,等号两边的分子和分母分别交叉相乘,所得的积相等。
16.C
【分析】由题意可知,11时的气温=9时的气温-11时比9时下降的气温,求出9时去掉负号后的气温与下降气温的和,最后再加上负号即可。
【详解】4+3=7(摄氏度)
所以,11时的气温是﹣7摄氏度。
故答案为:C
【点睛】本题主要考查正负数的简单计算,掌握负数减负数的计算方法是解答题目的关键。
17.B
【分析】根据判断两种量成正比例还是成反比例的方法:关键是看这两种相关联的量中相对应的两个数的商一定还是积一定,如果商一定,就成正比例关系;如果积一定,就成反比例关系;据此对各题进行依次分析,进而得出结论。
【详解】A、和一定,两个加数不成比例;
B、因为圆的周长÷直径=π(一定),所以圆的周长和直径成正比例,符合题意;
C、一个人的年龄和他认识的字不成比例;
D、当三角形的面积一定时,三角形的底与高成反比例。
【点睛】此题考查了判断两种量成正比例还是成反比例的方法。
18.C
【分析】由题意可知,一根木料锯成5段,则需要锯5-1=4次,则锯成10段需要锯10-1=9次,锯一次所需要的时间是相同的,则锯木料用的时间与锯的次数成正比例,据此列比例解答即可。
【详解】=
解:4=
x=4×9
x=36
故答案为:C
【点睛】本题考查用比例解决实际问题,明确锯木料用的时间与锯的次数成正比例是解题的关键。
19.C
【分析】已知物体的体积=上升部分水的体积,物体的体积=底面积×上升部分的高度,根据圆柱的体积公式,用底面积×上升部分的高度即可求出石头的体积,据此解答。
【详解】125.6÷3.14÷2
=40÷2
=20(厘米)
3.14×202×(23-20)
=3.14×400×3
=1256×3
=3768(立方厘米)
这块石头的体积是3768立方厘米。
故答案为:C
20.C
【分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是学校。根据图上距离和比例尺的关系确定实际距离。
【详解】A.50×2=100(米)
医院在学校西偏北20°方向100m处。所以原说法错误。
B.50×3=150(米)
邮局在学校西偏南20°方向150m处。所以原说法错误。
C.50×2=100(米)
公园在学校北偏东45°方向100m处。所以原说法正确。
D.50×2=100(米)
广场在学校南偏东45°方向100m处,则学校在广场北偏西45°方向100m处。所以原说法错误。
故答案为:C
【点睛】本题主要考查图上距离、实际距离与比例尺之间的关系,并会根据物体的位置描述方向。
21.C
【解析】略
22.B
【详解】根据正、负数的意义,可得0不是正数,也不是负数;然后根据正数>0>负数,可得0比所有的负数大,据此解答即可.
23.B
【分析】根据圆柱的体积公式V=sh,与圆锥的体积公式V=sh,知道当圆柱与圆锥的体积相等时,底面积的比和高的比是成反比的关系,由此即可解答.
【详解】因为,圆锥体和圆柱的高的比是:9:1,
圆柱的体积公式是:V=sh,
圆锥的体积公式是:V=sh,
所以,圆锥体和圆柱的底面积的比是:1:3,
即圆柱体底面积和圆锥体底面积的比是:3:1,
24.A
【分析】根据比例的性质、图形的放大、圆柱和圆锥的体积关系以及分数的基本性质,一一判断各叙述的正误,再选出正确选项即可。
【详解】(1)根据比例的性质,比例的两内项和两外项同时变更位置,比例仍然成立。所以,原说法正确;
(2)长方形按2∶1放大后,长和宽都扩大到原来的2倍,此时面积扩大到原来的4倍。所以,原说法错误;
(3)如果一个圆柱的体积是圆锥的3倍,它们的底和高不一定存在关系。所以,原说法错误;
(4)分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。所以,原说法错误。
所以,只有一个叙述是正确的。
故答案为:A
【点睛】本题考查了比例的性质、图形的放大、圆柱和圆锥的体积关系以及分数的基本性质,明确各个性质和概念是解题的关键。
25.A
【详解】试题分析:根据题意,可设圆柱的半径为r,高为h,根据圆柱的体积=底面积×高计算出圆柱原来的体积与改变后的体积,然后再用改变后的体积除以原来的体积即可得到答案。
解:可设圆柱的半径为r,高为h
圆柱原来的体积为:πr2h
改变后的圆柱的体积为:9πr2×h=3πr2h
体积扩大了:3πr2h÷πr2h=3
即一个圆柱的半径扩大3倍,高缩小3倍,体积就会扩大3倍。
故选A。
点评:此题主要考查的是圆柱的体积公式及其灵活应用。
26.D
【分析】利息=本金×年利率×时间,由此代入数据求出利息,再加上本金即可解答。
【详解】2000×2.75%×3+2000
=2000×0.0275×3+2000
=165+2000
=2165(元)
到期后,李伟一共可以取出2165元。
故答案为:D
【点睛】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×时间(注意时间和利率的对应)。
27.B
【分析】正数、负数表示两种相反意义的量;比0℃低的温度叫零下温度,通常在数字前面加“﹣”(负号);比0℃高的温度叫零上温度,通常在数字前面加“﹢”(正号),也可以省略不写。
﹣3℃与0℃相差3℃,8℃与0℃相差8℃,所以最低气温与最高气温的温差是(3+8)℃。
【详解】3+8=11℃
故答案为:B
【点睛】掌握正负数的意义以及温差的计算方法。
28.A
【分析】用长方形的纸围成一个最大的圆柱,圆柱的侧面积等于这张纸的面积,因为这两张纸的大小一样,所以这两个长方形的面积相等,即圆柱的侧面积相等,据此解答。
【详解】分析可知,两张同样大小的长方形纸,分别围成一个最大的圆柱,圆柱的侧面积都等于长方形的面积,所以这两个圆柱的侧面积一定相等。
故答案为:A
【点睛】本题主要考查圆柱的侧面积,理解圆柱的侧面积等于长方形的面积是解答题目的关键。
29.B
【分析】图上距离∶实际距离=比例尺,因为实际距离不变,所以图上距离与实际距离成正比,则甲图上北京到上海的图距是乙图上这两地之间图距的几分之几,用甲图的比例尺除以乙图的比例尺即可。
【详解】
故答案为:B
30.D
【详解】试题分析:设圆锥的体积为V,底面积为S,则圆柱的体积是2V,底面积是S,利用圆柱和圆锥的体积公式推导出它们高的比是几比几,即可解答.
解:设圆锥的体积为V,底面积为S,则圆柱的体积是2V,底面积是S,
则圆锥的高为:,
圆柱的高为:=,
则圆锥的高与圆柱的高的比是::=2:1,
因为圆柱的高是9厘米,
所以圆锥的高是:9×2=18(厘米),
答:圆柱的高是18厘米.
故选D.
点评:此题主要考查了圆柱和圆锥的体积公式的灵活应用,利用公式推导出它们高的比是解决此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
