初中数学北师大版九年级下册 第一章 直角三角形的边角关系---几何测量问题复习(第一课时)复习教案
文档属性
| 名称 | 初中数学北师大版九年级下册 第一章 直角三角形的边角关系---几何测量问题复习(第一课时)复习教案 |  | |
| 格式 | docx | ||
| 文件大小 | 379.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 15:17:47 | ||
图片预览


文档简介
几何测量问题复习
教学内容和学情分析
本节课是基于北师大版九年级下册《直角三角形的边角关系》以勾股定理、相似三角形、比例关系为基础,引入角度与边长的比值(三角函数)。也是为高中三角函数(如正弦定理、余弦定理)的学习奠定基础。学生已掌握直角三角形的性质(勾股定理、两锐角互余)。熟悉比例与相似三角形的概念(理解“比值”的数学意义)。能进行简单的代数运算和几何证明,但抽象思维和复杂问题转化能力较弱。学生也具备初步的数形结合意识,但对实际问题的数学建模缺乏经验。
学习目标
探索并认识锐角三角函数(sin A,cos A,tan A),知道 30°,45°,60°角的三角函数值
会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角
能用锐角三角函数解直角三角形.
教学重难点
重点:利用三角函数解决实际问题
难点:实际问题中如何构造直角三角形并选择正确的三角函数
教学过程
1、思路梳理
知识回顾
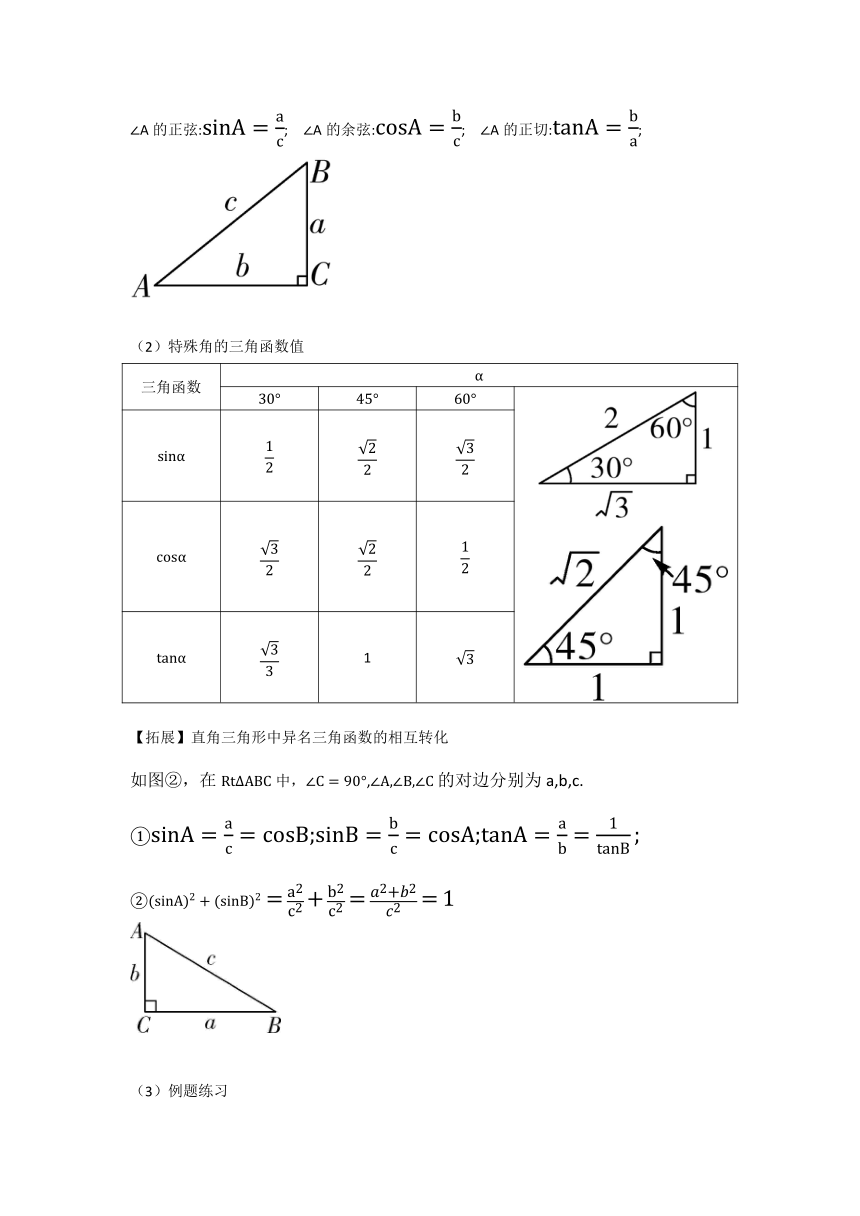
(1)锐角三角函数
定义:在中,,A为中的一锐角,则
A的正弦:; A的余弦:; A的正切:;
特殊角的三角函数值
三角函数
1
【拓展】直角三角形中异名三角函数的相互转化
如图②,在中,,的对边分别为a,b,c.
①
②
例题练习
如图,AD是△ABC的高。若BD=2CD=6,,则边AB的长为()
A、 B、 C、 D、
2. 如图,在中, 则的值为 ( )
A、 B、 C、 D、
3 . 如图,在△ABC中, AD平分,交BC于点D,DE⊥AB,垂足为E .若DE=1,则BC的长为 ( )
A、 B、 C、 D、3
4.如图,在6×7的网格中,每个小正方形的边长均为1. 若点A,B,C都在格点上,则sin B 的值为 ( )
A、 B、 C、 D、
(4)锐角三角函数的实际应用
1、 方向角:如图2,A点位于O点的北偏东30方向,B点位于O点的南偏东60°方向,C 点位于O点的北偏西45°方向 (或西北方向)
2、仰角、俯角:如图3,在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角
3、坡度(坡比)、坡角:如图4,坡面的铅直高度和水平宽度的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角 叫坡角,
例、综合与实践
数学实践活动小组要测量商业大厦MN的高度,小组成员各抒己见,提出不同的测量方案,请你结合题中数据和他们一起完成测量活动.
【方案1】 小明同学的方案,利用测角仪测量.
如图①,小明在水平面A处安置测角仪测得大厦MN顶部点N的仰角为,
小明眼睛到地面的距离AB=1.7m,BM的距离是14m,请帮助小明计算他所测量
商业大厦MN的高度. (精确到1m参考数据:)
【方案2】 小华同学的方案:差距测量法.
如图②,在点A处测得大厦MN顶端的仰角为,在点C处测得大厦MN顶端的仰角为,经测量AC=59m,试求商业大厦MN的高度.
(,结果精确到1m)
项目主题:测量学校旗杆高度
问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如标杆,镜子,测角仪…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的其中一种测量方案:
方案
测量工具 测量角度的仪器,皮尺
测量方案示意图
说明 点C、D、A在同一条直线上,
测量数据
参考数据
任务解决:计算学校旗杆的高度AB。(结果保留整数)
1、一座吊桥的钢索立柱AD两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索AB的长度.他们测得为BD为,由于B,D两点间的距离不易测得,通过探究和测量,发现CD恰好为,点B与点C之间的距离约为16m.已知点B,C,D共线,.求钢索AB的长度. (结果保留根号)
2、某景区为给游客提供更好的游览体验,计划以山脚A为起点,沿途修建AB,CD两段长
度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC(如图).索道AB与AF的夹角为,CD与水平线的夹角为,BE,DF分别垂直于水平地面AF(点A,E,F在同一水平直线上),且BE=140m,请你帮忙求出山顶D到水平地面的距离DF(结果精确到1m;参考数据:)
3、一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯(灯杆底部不可到达)的高AB.如图所示,当小明爸爸站在点D处时,他在该景观灯照射下的影子长为DF,测得DF=2.4;当小明站在爸爸影子的顶端F处时,测得点A的仰角为.已知爸爸的身高CD=1.8m,小明眼睛到地面的距离EF=1.6m,点F、D、B在同一条直线上,求该景观灯的高AB(参考数据: )
板书设计
几何测量问题复习(第一课时)
知识回顾
例题解析
实际应用
作业布置
万维分层作业本第86、87页
教学反思
教学内容和学情分析
本节课是基于北师大版九年级下册《直角三角形的边角关系》以勾股定理、相似三角形、比例关系为基础,引入角度与边长的比值(三角函数)。也是为高中三角函数(如正弦定理、余弦定理)的学习奠定基础。学生已掌握直角三角形的性质(勾股定理、两锐角互余)。熟悉比例与相似三角形的概念(理解“比值”的数学意义)。能进行简单的代数运算和几何证明,但抽象思维和复杂问题转化能力较弱。学生也具备初步的数形结合意识,但对实际问题的数学建模缺乏经验。
学习目标
探索并认识锐角三角函数(sin A,cos A,tan A),知道 30°,45°,60°角的三角函数值
会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角
能用锐角三角函数解直角三角形.
教学重难点
重点:利用三角函数解决实际问题
难点:实际问题中如何构造直角三角形并选择正确的三角函数
教学过程
1、思路梳理
知识回顾
(1)锐角三角函数
定义:在中,,A为中的一锐角,则
A的正弦:; A的余弦:; A的正切:;
特殊角的三角函数值
三角函数
1
【拓展】直角三角形中异名三角函数的相互转化
如图②,在中,,的对边分别为a,b,c.
①
②
例题练习
如图,AD是△ABC的高。若BD=2CD=6,,则边AB的长为()
A、 B、 C、 D、
2. 如图,在中, 则的值为 ( )
A、 B、 C、 D、
3 . 如图,在△ABC中, AD平分,交BC于点D,DE⊥AB,垂足为E .若DE=1,则BC的长为 ( )
A、 B、 C、 D、3
4.如图,在6×7的网格中,每个小正方形的边长均为1. 若点A,B,C都在格点上,则sin B 的值为 ( )
A、 B、 C、 D、
(4)锐角三角函数的实际应用
1、 方向角:如图2,A点位于O点的北偏东30方向,B点位于O点的南偏东60°方向,C 点位于O点的北偏西45°方向 (或西北方向)
2、仰角、俯角:如图3,在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角
3、坡度(坡比)、坡角:如图4,坡面的铅直高度和水平宽度的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角 叫坡角,
例、综合与实践
数学实践活动小组要测量商业大厦MN的高度,小组成员各抒己见,提出不同的测量方案,请你结合题中数据和他们一起完成测量活动.
【方案1】 小明同学的方案,利用测角仪测量.
如图①,小明在水平面A处安置测角仪测得大厦MN顶部点N的仰角为,
小明眼睛到地面的距离AB=1.7m,BM的距离是14m,请帮助小明计算他所测量
商业大厦MN的高度. (精确到1m参考数据:)
【方案2】 小华同学的方案:差距测量法.
如图②,在点A处测得大厦MN顶端的仰角为,在点C处测得大厦MN顶端的仰角为,经测量AC=59m,试求商业大厦MN的高度.
(,结果精确到1m)
项目主题:测量学校旗杆高度
问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如标杆,镜子,测角仪…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的其中一种测量方案:
方案
测量工具 测量角度的仪器,皮尺
测量方案示意图
说明 点C、D、A在同一条直线上,
测量数据
参考数据
任务解决:计算学校旗杆的高度AB。(结果保留整数)
1、一座吊桥的钢索立柱AD两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索AB的长度.他们测得为BD为,由于B,D两点间的距离不易测得,通过探究和测量,发现CD恰好为,点B与点C之间的距离约为16m.已知点B,C,D共线,.求钢索AB的长度. (结果保留根号)
2、某景区为给游客提供更好的游览体验,计划以山脚A为起点,沿途修建AB,CD两段长
度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC(如图).索道AB与AF的夹角为,CD与水平线的夹角为,BE,DF分别垂直于水平地面AF(点A,E,F在同一水平直线上),且BE=140m,请你帮忙求出山顶D到水平地面的距离DF(结果精确到1m;参考数据:)
3、一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯(灯杆底部不可到达)的高AB.如图所示,当小明爸爸站在点D处时,他在该景观灯照射下的影子长为DF,测得DF=2.4;当小明站在爸爸影子的顶端F处时,测得点A的仰角为.已知爸爸的身高CD=1.8m,小明眼睛到地面的距离EF=1.6m,点F、D、B在同一条直线上,求该景观灯的高AB(参考数据: )
板书设计
几何测量问题复习(第一课时)
知识回顾
例题解析
实际应用
作业布置
万维分层作业本第86、87页
教学反思
