吉林省吉林市东北三省教育教学联合体2025届5月联考模拟预测数学试题(含答案)
文档属性
| 名称 | 吉林省吉林市东北三省教育教学联合体2025届5月联考模拟预测数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 712.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 15:49:46 | ||
图片预览



文档简介
2025届吉林省吉林市东北三省教育教学联合体5月联考模拟预测数学试题
一、单选题
1.已知集合,,则( )
A. B. C. D.
2.已知 ,则( )
A. B. C. D.
3.样本数据19,20,21,23,13,16,24,28的第75百分位数为( )
A.20 B.21 C.23 D.23.5
4.已知侧棱长为,底面边长为的正三棱锥,其内切球球心为,球与球以及三棱锥的三个侧面均相切,则( )
A. B. C. D.
5.已知函数,是偶函数,则的最大值为( )
A. B. C.1 D.
6.函数,若在有最大值,则实数的取值范围是( )
A. B. C. D.
7.已知双曲线的左 右焦点分别为,以为直径的圆与双曲线在第一 三象限的交点分别为,则的周长为( )
A. B.8 C. D.
8.莫比乌斯(Mobius)环是最具有代表性的单侧曲面之一,它由德国数学家莫比乌斯于1858年发现. 就是把一根纸条扭转180°后,两头再粘接起来做成的纸带圈.现将一个长为30cm、宽为4cm的矩形纸条粘合两端(粘合两端重叠部分忽略不计),形成一个莫比乌斯环,如图:
下列关于莫比乌斯环说法正确的是( )
A.一只小虫在不跨过它的边缘情况下沿着表面至少走30cm就能回到原处
B.如果把它沿中线剪开(如图白色线的部分),曲面被分成独立的两部分
C.如果把它沿中线剪开(如图白色线的部分),最终得到纸带的边缘周长为120cm
D.一只小虫在不跨过它的边缘情况下不能爬遍整个曲面
二、多选题
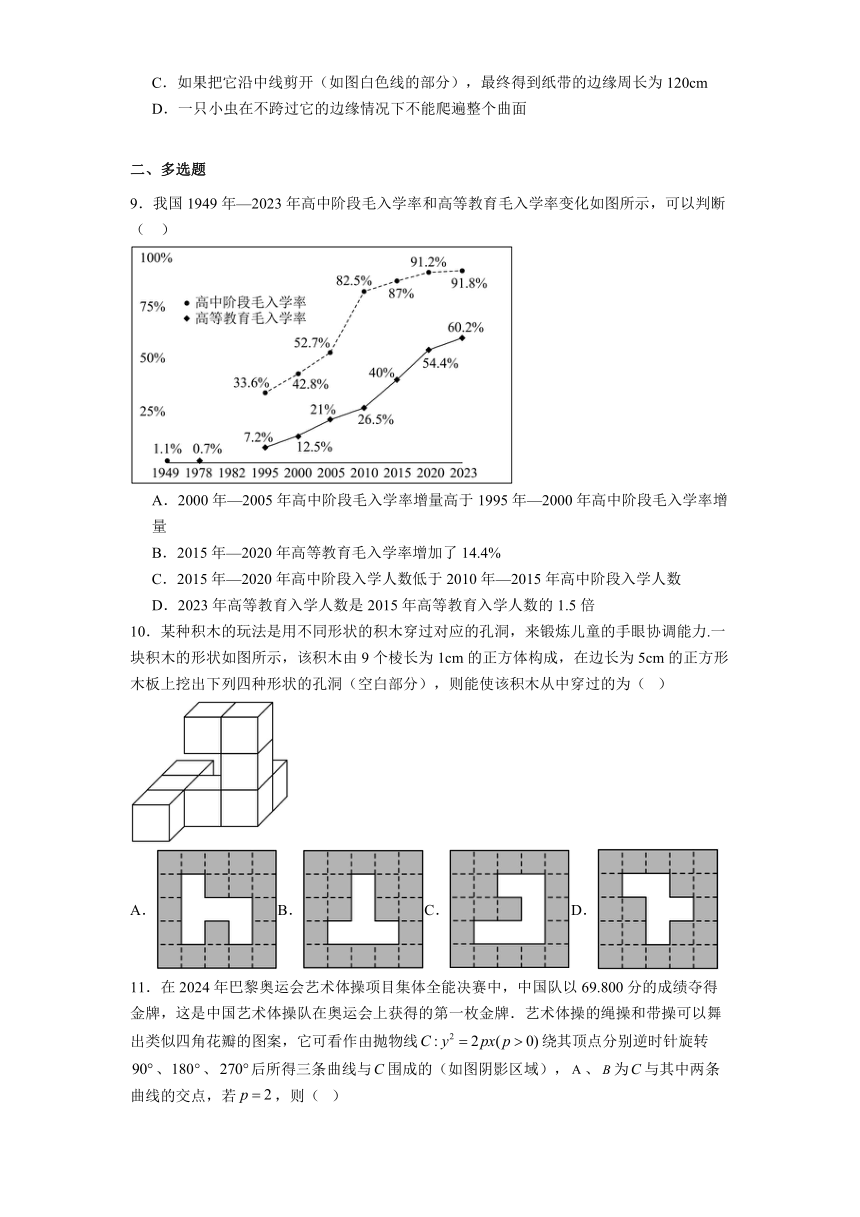
9.我国1949年—2023年高中阶段毛入学率和高等教育毛入学率变化如图所示,可以判断( )
A.2000年—2005年高中阶段毛入学率增量高于1995年—2000年高中阶段毛入学率增量
B.2015年—2020年高等教育毛入学率增加了14.4%
C.2015年—2020年高中阶段入学人数低于2010年—2015年高中阶段入学人数
D.2023年高等教育入学人数是2015年高等教育入学人数的1.5倍
10.某种积木的玩法是用不同形状的积木穿过对应的孔洞,来锻炼儿童的手眼协调能力.一块积木的形状如图所示,该积木由9个棱长为1cm的正方体构成,在边长为5cm的正方形木板上挖出下列四种形状的孔洞(空白部分),则能使该积木从中穿过的为( )
A.B.C.D.
11.在2024年巴黎奥运会艺术体操项目集体全能决赛中,中国队以69.800分的成绩夺得金牌,这是中国艺术体操队在奥运会上获得的第一枚金牌.艺术体操的绳操和带操可以舞出类似四角花瓣的图案,它可看作由抛物线绕其顶点分别逆时针旋转、、后所得三条曲线与围成的(如图阴影区域),、为与其中两条曲线的交点,若,则( )
A.开口向上的抛物线的方程为
B.
C.直线截第一象限花瓣的弦长最大值为
D.阴影区域的面积不大于32
三、填空题
12.若,则 .
13.已知圆锥与圆柱的底面半径相等,它们的高也相等,若圆柱的底面积为,侧面积为,则圆锥的表面积为 .
14.已知,,且动点满足.则的取值范围为 ;若线段PM的垂直平分线与PA交于点Q,则的正切值的最大值为 .
四、解答题
15.已知、、分别为斜中角、、的对边,.
(1)求;
(2)已知的面积为,求的最小值.
16.如图,在四棱锥中,底面是菱形,,平面.
(1)证明:;
(2)若为的中点,,求直线与平面所成角的正弦值.
17.2025年4月24日,搭载“神舟二十号”的火箭发射升空,有很多民众通过手机、电视等方式观看有关新闻.某机构将关注这件事的时间在2小时以上的人称为“航天爱好者”,否则称为“非航天爱好者”,该机构通过调查,从参与调查的人群中随机抽取200人进行分析,得到下表(单位:人):
航天爱好者 非航天爱好者 合计
女 40 60 100
男 70 30 100
合计 110 90 200
(1)能否有99%的把握认为“航天爱好者”或“非航天爱好者”与性别有关?
(2)现从这100名男生与100名女生中,按“航天爱好者”和“非航天爱好者”这两种类型分别进行分层抽样抽取男生10人,女生5人.将这15人中航天爱好者记为A组,非航天爱好者记为B组.现从这两组中各任意选取一人进行交换,求经过一次交换后,A组中女生人数的分布列和数学期望.
附:,其中,
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18.已知函数,.
(1)当时,求在上的值域;
(2)证明:曲线与在点处存在公切线.
19.17世纪,牛顿在《流数法与无穷级数》一书中,给出了代数方程的一种数值解法:如图所示,我们想要找到的根,即点的横坐标,则可以先在点附近取一个初始值,比如横坐标为处,然后在以为横坐标的点处做一条切线,并求出该切线与轴的交点,此时,我们会发现比初始值更接近点.如果重复这个过程,不断绘制切线并计算其与轴的交点,依次迭代下去,我们将得到,根据给定的精确度,直到求得满足精度的近似解为止.这就是牛顿迭代法(切线法)的原理.已知,取.
(1)根据牛顿迭代法,求;
(2)求与的关系式;
(3)牛顿迭代法中蕴含了“以直代曲”的数学思想,直线常常取曲线的切线或割线.若,求证:.
参考答案
1.B
2.C
3.D
4.B
5.B
6.B
7.C
8.C
9.AB
10.ABC
11.ACD
12.
13.
14./
15.(1)因为,
由正弦定理得,,
即,
因为为斜三角形,所以,故,
由正弦定理可得.
(2)由(1)知,,所以,
所以,
即,
因为,则,故,所以,
所以,则,
所以,
当且仅当,即时,取最小值.
16.(1)证明:连接,
是菱形,是对角线,
,
又平面平面,
,
又平面平面,
平面,
又平面.
(2)取中点,连接,则,
以为轴,以为轴,以为轴,建立如图空间直角坐标系,
令,则,
,
设平面的法向量为,
由,得,得,
.
17.(1)
所以有99.9%的把握认为“航天爱好者”或“非航天爱好者”与性别有关.
(2)按分层抽样,100名男生中,抽取“航天爱好者”有7人,“非航天爱好者”有3人,
100名女生中,抽取“航天爱好者”有2人,“非航天爱好者”有3人.
故A组有男生7人,女生2人,B组有男生3人,女生3人.
从这两组中各任意选取一人进行交换,经过一次交换后,
A组中女生人数为,则的可能值为1,2,3.
,,.
X的分布列如下表:
1 2 3
.
18(1)若,则,得,
令,解得,
所以当时,,则单调递增,
当时,,则单调递减,
所以当时,有最大值,,
当时,,当时,,
故在上的值域为.
(2)证明:由,得,则,
又,故在点处的切线方程为.
同理,由,得,则,
又,故在点处的切线方程为,
所以与在处存在公切线.
19.(1),,,
当时,,,
因此切线,
当时,可得;
(2)当切点为时切线方程为:.
当时,可得:
,
即;
(3)证明:由(1)知,函数在处的切线方程为.
①先证:当的图象恒在切线的上方,
即当时,,即.
令,则,
易知,令,
可得,易知,
在单调递减,在单调递增,
又,,,
存在使得,
在单调递增,在单调递减,在单调递增.
又,
当时,,即,即.
②下证:.
即,即.
令,
则,则在单调递减,在单调递增,
又,
显然当时,恒成立,即恒成立,
由①②可得.
一、单选题
1.已知集合,,则( )
A. B. C. D.
2.已知 ,则( )
A. B. C. D.
3.样本数据19,20,21,23,13,16,24,28的第75百分位数为( )
A.20 B.21 C.23 D.23.5
4.已知侧棱长为,底面边长为的正三棱锥,其内切球球心为,球与球以及三棱锥的三个侧面均相切,则( )
A. B. C. D.
5.已知函数,是偶函数,则的最大值为( )
A. B. C.1 D.
6.函数,若在有最大值,则实数的取值范围是( )
A. B. C. D.
7.已知双曲线的左 右焦点分别为,以为直径的圆与双曲线在第一 三象限的交点分别为,则的周长为( )
A. B.8 C. D.
8.莫比乌斯(Mobius)环是最具有代表性的单侧曲面之一,它由德国数学家莫比乌斯于1858年发现. 就是把一根纸条扭转180°后,两头再粘接起来做成的纸带圈.现将一个长为30cm、宽为4cm的矩形纸条粘合两端(粘合两端重叠部分忽略不计),形成一个莫比乌斯环,如图:
下列关于莫比乌斯环说法正确的是( )
A.一只小虫在不跨过它的边缘情况下沿着表面至少走30cm就能回到原处
B.如果把它沿中线剪开(如图白色线的部分),曲面被分成独立的两部分
C.如果把它沿中线剪开(如图白色线的部分),最终得到纸带的边缘周长为120cm
D.一只小虫在不跨过它的边缘情况下不能爬遍整个曲面
二、多选题
9.我国1949年—2023年高中阶段毛入学率和高等教育毛入学率变化如图所示,可以判断( )
A.2000年—2005年高中阶段毛入学率增量高于1995年—2000年高中阶段毛入学率增量
B.2015年—2020年高等教育毛入学率增加了14.4%
C.2015年—2020年高中阶段入学人数低于2010年—2015年高中阶段入学人数
D.2023年高等教育入学人数是2015年高等教育入学人数的1.5倍
10.某种积木的玩法是用不同形状的积木穿过对应的孔洞,来锻炼儿童的手眼协调能力.一块积木的形状如图所示,该积木由9个棱长为1cm的正方体构成,在边长为5cm的正方形木板上挖出下列四种形状的孔洞(空白部分),则能使该积木从中穿过的为( )
A.B.C.D.
11.在2024年巴黎奥运会艺术体操项目集体全能决赛中,中国队以69.800分的成绩夺得金牌,这是中国艺术体操队在奥运会上获得的第一枚金牌.艺术体操的绳操和带操可以舞出类似四角花瓣的图案,它可看作由抛物线绕其顶点分别逆时针旋转、、后所得三条曲线与围成的(如图阴影区域),、为与其中两条曲线的交点,若,则( )
A.开口向上的抛物线的方程为
B.
C.直线截第一象限花瓣的弦长最大值为
D.阴影区域的面积不大于32
三、填空题
12.若,则 .
13.已知圆锥与圆柱的底面半径相等,它们的高也相等,若圆柱的底面积为,侧面积为,则圆锥的表面积为 .
14.已知,,且动点满足.则的取值范围为 ;若线段PM的垂直平分线与PA交于点Q,则的正切值的最大值为 .
四、解答题
15.已知、、分别为斜中角、、的对边,.
(1)求;
(2)已知的面积为,求的最小值.
16.如图,在四棱锥中,底面是菱形,,平面.
(1)证明:;
(2)若为的中点,,求直线与平面所成角的正弦值.
17.2025年4月24日,搭载“神舟二十号”的火箭发射升空,有很多民众通过手机、电视等方式观看有关新闻.某机构将关注这件事的时间在2小时以上的人称为“航天爱好者”,否则称为“非航天爱好者”,该机构通过调查,从参与调查的人群中随机抽取200人进行分析,得到下表(单位:人):
航天爱好者 非航天爱好者 合计
女 40 60 100
男 70 30 100
合计 110 90 200
(1)能否有99%的把握认为“航天爱好者”或“非航天爱好者”与性别有关?
(2)现从这100名男生与100名女生中,按“航天爱好者”和“非航天爱好者”这两种类型分别进行分层抽样抽取男生10人,女生5人.将这15人中航天爱好者记为A组,非航天爱好者记为B组.现从这两组中各任意选取一人进行交换,求经过一次交换后,A组中女生人数的分布列和数学期望.
附:,其中,
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18.已知函数,.
(1)当时,求在上的值域;
(2)证明:曲线与在点处存在公切线.
19.17世纪,牛顿在《流数法与无穷级数》一书中,给出了代数方程的一种数值解法:如图所示,我们想要找到的根,即点的横坐标,则可以先在点附近取一个初始值,比如横坐标为处,然后在以为横坐标的点处做一条切线,并求出该切线与轴的交点,此时,我们会发现比初始值更接近点.如果重复这个过程,不断绘制切线并计算其与轴的交点,依次迭代下去,我们将得到,根据给定的精确度,直到求得满足精度的近似解为止.这就是牛顿迭代法(切线法)的原理.已知,取.
(1)根据牛顿迭代法,求;
(2)求与的关系式;
(3)牛顿迭代法中蕴含了“以直代曲”的数学思想,直线常常取曲线的切线或割线.若,求证:.
参考答案
1.B
2.C
3.D
4.B
5.B
6.B
7.C
8.C
9.AB
10.ABC
11.ACD
12.
13.
14./
15.(1)因为,
由正弦定理得,,
即,
因为为斜三角形,所以,故,
由正弦定理可得.
(2)由(1)知,,所以,
所以,
即,
因为,则,故,所以,
所以,则,
所以,
当且仅当,即时,取最小值.
16.(1)证明:连接,
是菱形,是对角线,
,
又平面平面,
,
又平面平面,
平面,
又平面.
(2)取中点,连接,则,
以为轴,以为轴,以为轴,建立如图空间直角坐标系,
令,则,
,
设平面的法向量为,
由,得,得,
.
17.(1)
所以有99.9%的把握认为“航天爱好者”或“非航天爱好者”与性别有关.
(2)按分层抽样,100名男生中,抽取“航天爱好者”有7人,“非航天爱好者”有3人,
100名女生中,抽取“航天爱好者”有2人,“非航天爱好者”有3人.
故A组有男生7人,女生2人,B组有男生3人,女生3人.
从这两组中各任意选取一人进行交换,经过一次交换后,
A组中女生人数为,则的可能值为1,2,3.
,,.
X的分布列如下表:
1 2 3
.
18(1)若,则,得,
令,解得,
所以当时,,则单调递增,
当时,,则单调递减,
所以当时,有最大值,,
当时,,当时,,
故在上的值域为.
(2)证明:由,得,则,
又,故在点处的切线方程为.
同理,由,得,则,
又,故在点处的切线方程为,
所以与在处存在公切线.
19.(1),,,
当时,,,
因此切线,
当时,可得;
(2)当切点为时切线方程为:.
当时,可得:
,
即;
(3)证明:由(1)知,函数在处的切线方程为.
①先证:当的图象恒在切线的上方,
即当时,,即.
令,则,
易知,令,
可得,易知,
在单调递减,在单调递增,
又,,,
存在使得,
在单调递增,在单调递减,在单调递增.
又,
当时,,即,即.
②下证:.
即,即.
令,
则,则在单调递减,在单调递增,
又,
显然当时,恒成立,即恒成立,
由①②可得.
同课章节目录
