北师大版六年级下册数学期末专题训练:作图题(含解析)
文档属性
| 名称 | 北师大版六年级下册数学期末专题训练:作图题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 12:44:25 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版六年级下册数学期末专题训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
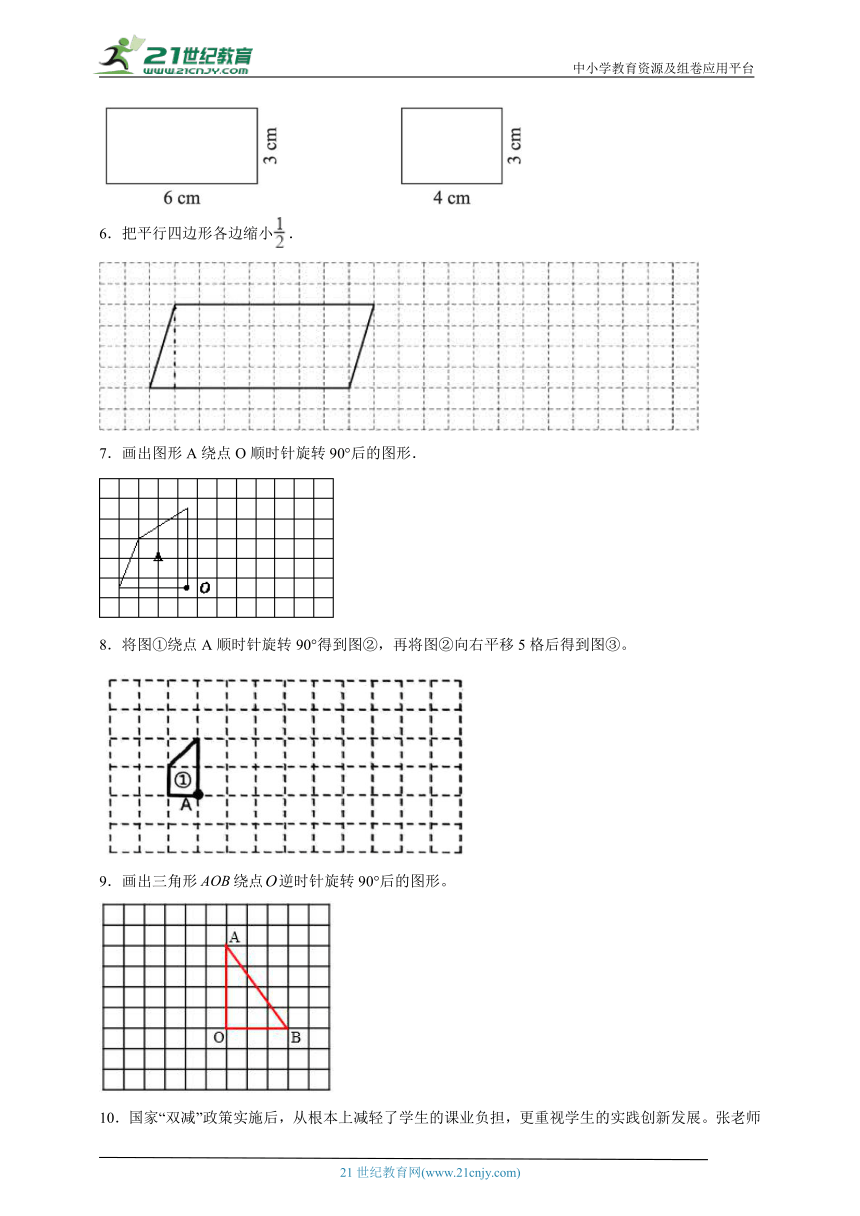
1.按要求画一画。
(1)以虚线MN为对称轴,画出图形A的轴对称图形B。
(2)将图形B绕点O逆时针旋转90°,得到图形C。
(3)将图形C向左平移6格,得到图形D。
2.自己按一定的规律设计一组图形,让同学来找一找规律。
3.如下图,剪纸是中华民族优秀的传统民间艺术之一,有很多的剪纸作品都可以看作是由一个基本图形经过平移、旋转或轴对称得到的(如下图)。你能设计这样一幅剪纸作品,并贴在下面吗?
4.按要求画一画。
(1)将图形①按1∶3缩小。
(2)将图形②按2∶1放大。
5.长方体的两个面如下图,请画出长方体的另外四个面。
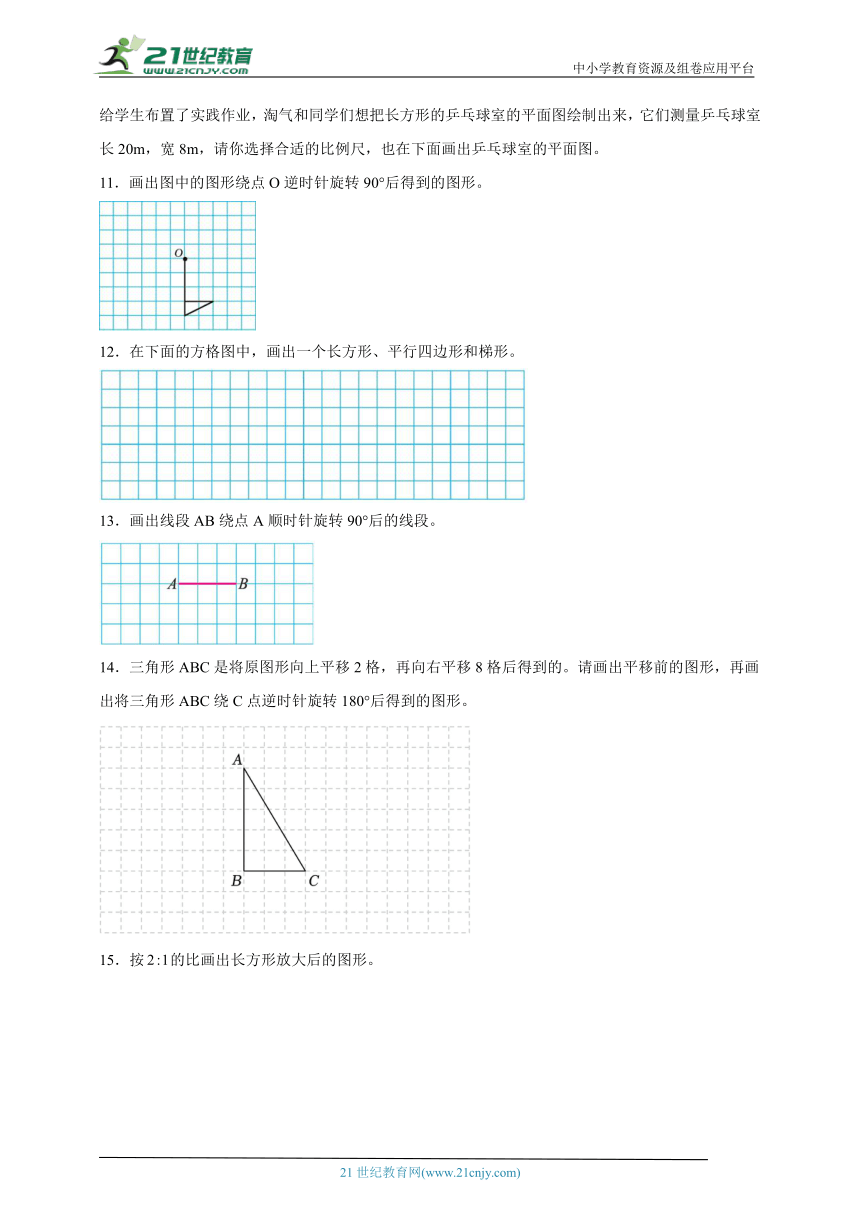
6.把平行四边形各边缩小.
7.画出图形A绕点O顺时针旋转90°后的图形.
8.将图①绕点A顺时针旋转90°得到图②,再将图②向右平移5格后得到图③。
9.画出三角形绕点逆时针旋转90°后的图形。
10.国家“双减”政策实施后,从根本上减轻了学生的课业负担,更重视学生的实践创新发展。张老师给学生布置了实践作业,淘气和同学们想把长方形的乒乓球室的平面图绘制出来,它们测量乒乓球室长20m,宽8m,请你选择合适的比例尺,也在下面画出乒乓球室的平面图。
11.画出图中的图形绕点O逆时针旋转90°后得到的图形。
12.在下面的方格图中,画出一个长方形、平行四边形和梯形。
13.画出线段AB绕点A顺时针旋转90°后的线段。
14.三角形ABC是将原图形向上平移2格,再向右平移8格后得到的。请画出平移前的图形,再画出将三角形ABC绕C点逆时针旋转180°后得到的图形。
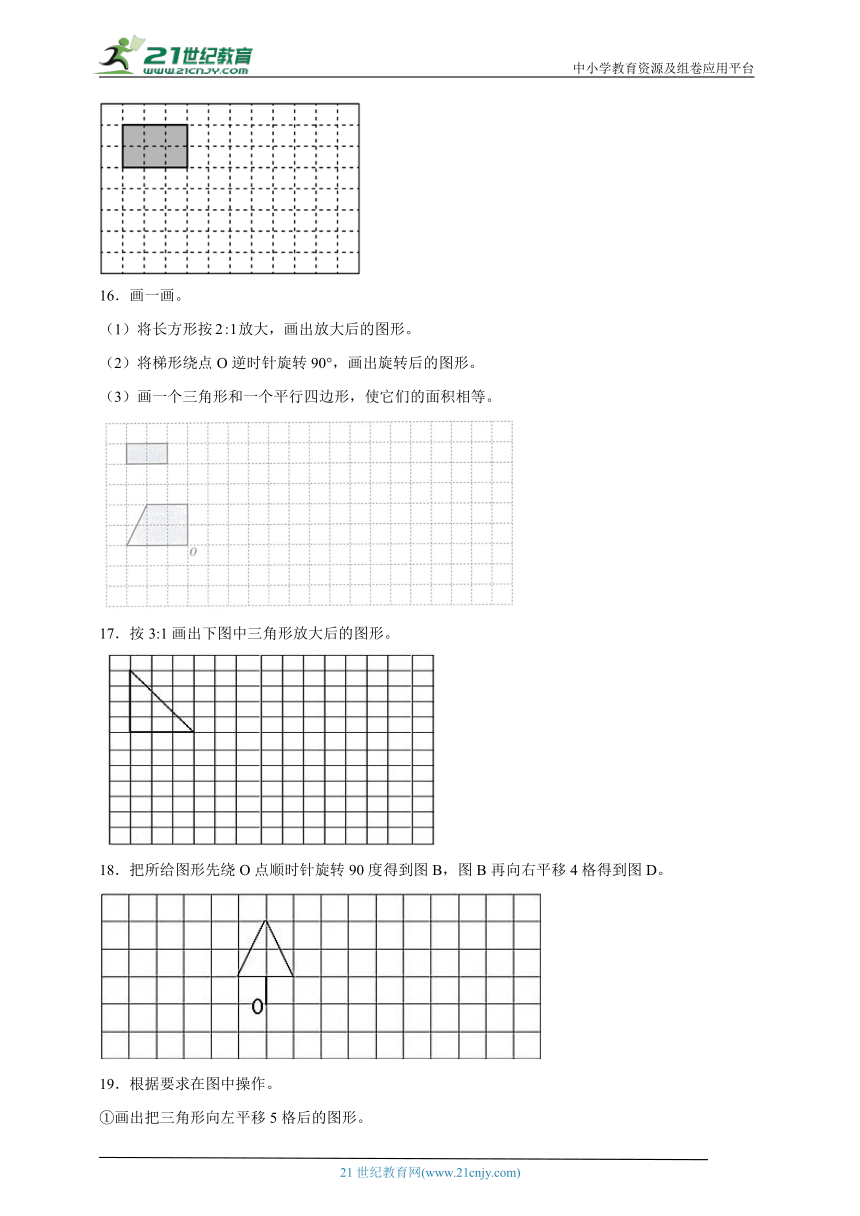
15.按的比画出长方形放大后的图形。
16.画一画。
(1)将长方形按放大,画出放大后的图形。
(2)将梯形绕点O逆时针旋转90°,画出旋转后的图形。
(3)画一个三角形和一个平行四边形,使它们的面积相等。
17.按3:1画出下图中三角形放大后的图形。
18.把所给图形先绕O点顺时针旋转90度得到图B,图B再向右平移4格得到图D。
19.根据要求在图中操作。
①画出把三角形向左平移5格后的图形。
②画出把三角形绕C点顺时针旋转90°后的图形。
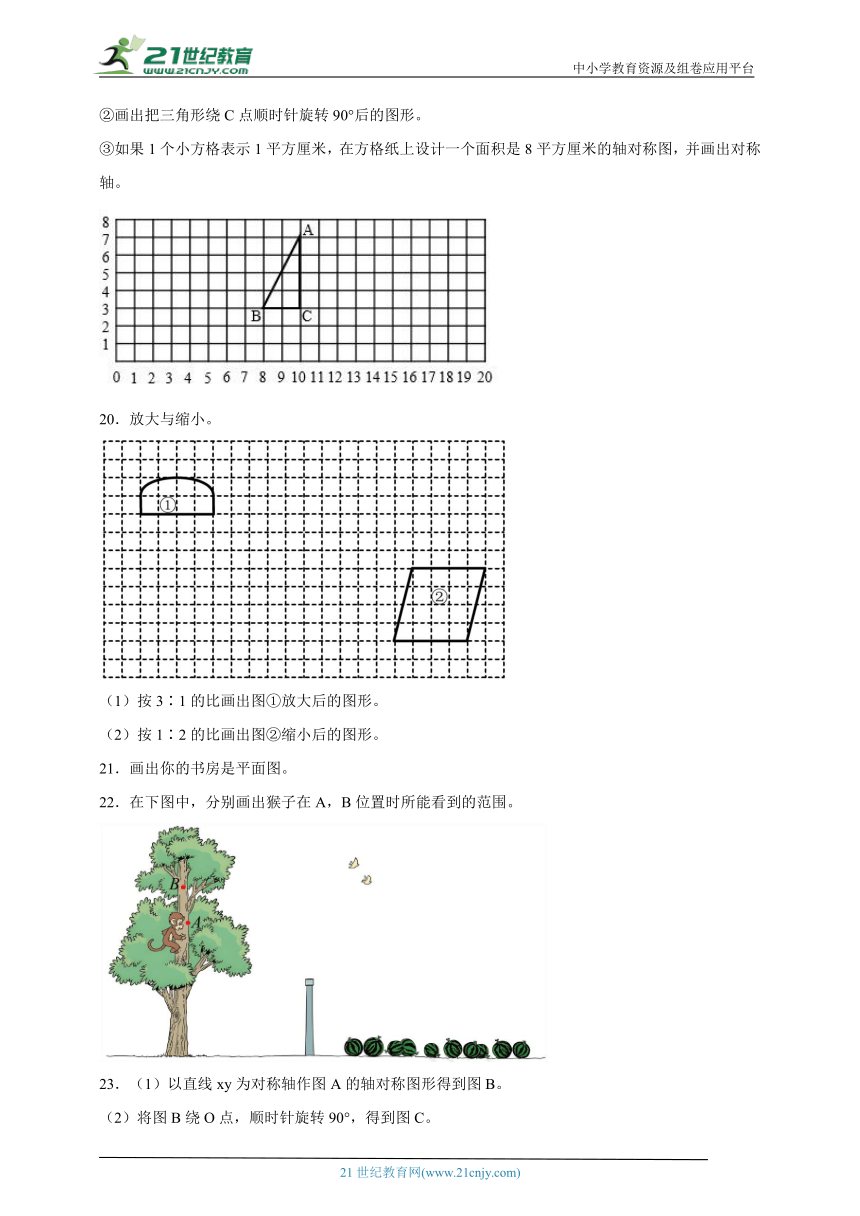
③如果1个小方格表示1平方厘米,在方格纸上设计一个面积是8平方厘米的轴对称图,并画出对称轴。
20.放大与缩小。
(1)按3∶1的比画出图①放大后的图形。
(2)按1∶2的比画出图②缩小后的图形。
21.画出你的书房是平面图。
22.在下图中,分别画出猴子在A,B位置时所能看到的范围。
23.(1)以直线xy为对称轴作图A的轴对称图形得到图B。
(2)将图B绕O点,顺时针旋转90°,得到图C。
(3)将图C向左平移7个格,得到图D。
24.画出这面小旗绕O点顺时针旋转90°后向左平移3格后得到的图形.
25.按要求画一画。
(1)画出图形A绕点O顺时针旋转90°后得到的图形B。
(2)画出图形B向右平移9格后得到的图形C。
26.画出房子的另一半。
27.将下面的正方形放大,使放大后的图形与原图形对应线段长的比为4∶1。
28.画出图形A关于直线l的轴对称图形,然后让新图绕o’点旋转900,连续旋转三次的图形.
29.在方格内按要求操作.
(i)把梯形按3:1放大,画出放大后的图形.
(ii)把三角形绕A点按逆时针方向连续旋转3次,每次都旋转 90° ,画出每次旋转后的图形,并标上序号①、②、③.
30.画出线段AB绕点B顺时针旋转90°后的线段。
31.按要求在方格纸上画图。
(1)将图形A绕O点逆时针旋转90°得到图形B。
(2)以直线L为对称轴作图形A的轴对称图形C,再将图形C向右平移4格得到图形D。
(3)画出图形E按2∶1放大后的图形F。
32.2022年6月5日10时44分,“神舟十四号”载人飞船开启了“天宫”空间站的新纪元,距地380千米高度的“天宫”空间站即将成型,我国的载人航天事业将正式进入“空间站”时代。请在下图中画出我国空间站距离地面的位置。
33.画出梯形绕点“O”逆时针旋转90°后得到的图形。
34.请你利用“图形运动”的相关知识,在如图的方格中自己设计一个图案,并把你设计图案时使用的图形的运动方式写出来。
35.画出图形ABCED绕A点顺时针旋转90°后的图形,并标出C点旋转后的位置C′点。
36.按要求画一画.
(1)把梯形绕A点顺时针旋转90°.
(2)把三角形绕B点逆时针旋转90°.
37.按要求操作.
(I)画出图(I)的另一半,使它成为一个轴对称图形.
(II)把图(II)绕O点逆时针旋转90°.
(III)把图(3)按3:1的比放大.
38.画出下面的线段AB绕点C顺时针旋转90°后的图形.
39.按要求在方格纸上画一画。
(1)将图①先向右平移8格,再向下平移3格
(2)以虚线MN为对称轴,画出图②的轴对称图形的另一半。
(3)将图③绕点O逆时针旋转
(4)将图③缩小,使得缩小后的图形与原图形对应线段长的比是1∶2。
40.王杰和同学测量了他们学校的一些主要建筑的长和宽以及方位,你能根据这些数据将这些建筑物在平面图上标出来吗?
教学楼在校门的正北方向150米处,教学楼长100米,宽60米。图书馆在校门的北偏东45度方向150米处,图书馆长60米,宽20米。体育馆在校门的西偏北40度方向200米处,体育馆长150米,宽100米。操场在校门的东偏北15度方向50米处,操场长200米,宽150米。
《北师大版六年级下册数学期末专题训练:作图题》参考答案
1.见详解
【分析】(1)根据轴对称图形的特征,各对称点到对称轴的距离相等,据此先描出各对称点的位置,然后顺次连接格点即可画出图形A的轴对称图形B;
(2)根据旋转的特征,将图形B绕点O逆时针旋转90°,点O的位置不变,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形C;
(3)根据平移的特征,将图形C各顶点向左平移6格,即可画出平移后的图形D。
【详解】画图如下:
【点睛】本题考查的目的是理解掌握图形的平移、旋转以及轴对称的性质及应用。
2.如图所示:
【详解】这个图形就是一个梯形旋转四次设计出的图形。
3.见详解
【分析】由给出的这两个图形可知,它们都是轴对称图形,都可以找到对称轴,再根据对称轴剪图形。因此要设计一幅剪纸作品,先找出对称轴,想象图形形状,再动手剪,最后摊开图形即可完成。
【详解】答案不唯一,满足条件即可,如图所示:
4.见详解
【分析】假设每个方格的边长为1,
(1)原梯形的上底、下底、高分别是6、3、6,缩小后是2、1、2。
(2)原三角形的两条直角边是2和4,扩大后分别是4和8。
【详解】(1)(2)如图:
【点睛】理解缩小与扩大的意义与方法是解决本题的关键。
5.见详解
【分析】长方体的特征:长方体有6个面,有三组相对的面完全相同,一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。
图中已知长方体的两个面分别是6×3、4×3的长方形,那么还各有一个6×3、4×3的长方形,另外有两个6×4的长方形,据此画出这四个面。
有两个相同的面
【详解】如图:
6.
【详解】各边都缩小,那么底边是4格,高是2格,由此画出缩小后的平行四边形即可.
7.
【详解】略
8.见详解
【分析】点A不动,将图形的各点绕着点A顺时针旋转90°,然后顺次连接各点,画出旋转后的图形;
将旋转后的图形各个顶点均向右平移5格,找出对应点,再依次连接,画出平移后的图形。
【详解】如图:
9.见详解
【分析】图形的旋转要满足三个条件:第一要找出图形旋转时所绕的旋转点;二要判断清楚图形的旋转方向;三是确定图形的旋转角度;在本题中,三角形是绕点O逆时针旋转90°。据此解答即可。
【详解】
【点睛】本题主要考查了旋转图形的画法,要画图形进行旋转后的图形,一定要找出图形的旋转点,旋转方向和旋转角度。
10.见详解
【分析】可以按照比例尺1∶400画出平面图。也就是图上1厘米的距离等于实际距离的400厘米。1m=100cm,高级单位转化为低级单位用乘法,则20m=2000cm,图上的距离用2000÷400=5(cm),8m=800cm,800÷400=2(cm)。再用有刻度的直尺画出平面图。
【详解】用比例尺为1∶400画图。
11.见详解
【分析】根据旋转的方法,将三角形与点O相连的边绕点O逆时针旋转90度,再将其它边连起来即可。
【详解】如图:
【点睛】做旋转后的图形时,一定要注意旋转的方向和角度,图形的大小和形状不变。
12.见详解
【分析】长方形的特征是两组对边分别平行、四个角都是直角的四边形。
平行四边形的特征是两组对边互相平行且相等。
梯形是只有一组对边互相平行的四边形;据此画图。
【详解】如图:
(画法不唯一)
13.见详解
【分析】根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°),找出点B的对应点B’,连接AB’,据此作图。
【详解】作图如下:
14.见详解
【分析】把三角形ABC按原路返回,返回时平移的方向相反,距离不变。根据平移的特征把三角形ABC的各顶点分别向左平移8格,再向下平移2格,依次连接即可得到平移前的图形;根据旋转的特征,三角形ABC绕点C逆时针旋转180°,点C的位置不动,这个图形的各部分均绕此点按逆时针方向旋转180°即可画出旋转后的图形。
【详解】根据题意画图如下:
15.见详解
【分析】根据图可知,这个长方形的长是3格,宽是2格,按2∶1的比扩大长方形,则长方形的长和宽都扩大到原来的2倍,此时的长是:3×2=6(格),宽:2×2=4(格),据此画图即可。
【详解】由分析可知:如下图所示:
【点睛】本题主要考查图形的放大,要注意是图形每条边都放大相应的倍数。
16.见详解
【分析】(1)将长方形的长和宽均放大到原来的2倍,画出放大后的图形;
(2)点O不动,将梯形的各边均逆时针旋转90°,画出旋转后的图形;
(3)三角形面积=底×高÷2,平行四边形面积=底×高,那么可以取三角形底为4,高为2,面积为4×2÷2=4,取平行四边形底为4,高为1,面积为4×1=4。此时,画出的三角形和平行四边形的面积相等。
【详解】如图:
(三角形和平行四边形的画法不唯一)
17.
【详解】略
18.见详解
【分析】(1)根据旋转的意义,图形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕点O按相同的方向旋转相同的度数,即可画出旋转后的图形B;
(2)根据图形平移的特征,把图形B的各顶点分别向右平移4格,再依次连接即可得到平移后的图形D。
【详解】
【点睛】本题考查了旋转和平移的意义,明确旋转和平移的定义是作图的关键。
19.见详解
【分析】①根据平移图形的特征,把△ABC的三个顶点分别向左平移5格,得到三个对应点A′B′C′,首尾连接这三点所得到的△A′B′C′就是△ABC的三个顶点分别向左平移5格得到的图形。
②根据旋转图形的特征,把△A′B′C′绕C′点顺时针旋转90°,C′点不动,△A′B′C′各边均绕C′点顺时针旋转90°,即A′C′旋转到A″C′的位置,B′C′旋转到B″C′R 的位置,连接A″B″,△A″B″C′就是△A′B′C′绕C′点顺时针旋转90°后的图形。
③画一个长是4厘米,宽是2厘米的长方形就是一个面积为8平方厘米的轴对称图形(答案不唯一)。
【详解】画图如下:
【点睛】本题是考查作图形的平移、旋转及轴对称图形,掌握图形的平移、旋转以及画轴对称图形的方法是解题的关键。
20.见详解
【分析】(1)根据图形放大的意义,把图形的上、下底及高均放大到原来的3倍,对应角大小不变,所得到的图形就是原图形按3∶1放大后的图形。
(2)根据图形缩小的意义,把平行四边形的各边均缩小到原来的,对应角大小不变,所得到的图形就是原图形按1∶2缩小后的图形。
【详解】(1)(2)如图:
【点睛】图形放大或缩小指对应边(线段)放大或缩小,对应角大小不变,即图形放大或缩小后,改变的是大小,形状不变。
21.
【详解】画平面图的时候,先要测量并记录数据,然后再确定以多大的比例画图,最后根据比例手工绘制样图。(答案不唯一)
22.见详解
【分析】观测点越高,观察的范围越大,观察点越低,观察的范围越小,随着观测点的变化观察范围也在变化。据此画出A、B两地和围墙外最高点连线交地平面即可。
【详解】如图:
23.(1)见详解;(2)见详解;(3)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,依次连接即可;
(2)根据旋转的特征,图B绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图C;
(3)根据平移的特征,把图C的各顶点分别向左平移7个格,依次连接即可得到平移后的图D。
【详解】如图:
【点睛】此题是考查了图形的平移、旋转以及作轴对称图形,要掌握相关知识点。
24.
【详解】本题考查平移和旋转的相关知识,将简单图形平移或旋转一定的度数.
25.(1)(2)见详解
【分析】(1)根据旋转的特征,图形A绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形B。
(2)根据平移的特征,把图形B的各顶点分别向右平移9格,依次连接即可得到平移后的图形。
【详解】
【点睛】图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。图形平移注意三要素:即原位置、平移方向、平移距离。
26.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
27.见详解
【分析】把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1。
【详解】
28.
【详解】略
29.(i)梯形按3:1放大后的图形如图红色部分;
(ii) 三角形绕A点按逆时针方向连续旋转3次的图形如图①、②、③
【分析】①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.
【详解】(1)按3:1的比例画出梯形放大后的图形,就是把原梯形的上底、下底和高分别扩大到原来的3倍,原梯形的上底、下底和高分别是2格、3格和1格,扩大后的梯形的上底、下底和高分别是6格、9格和3格.
(2)根据旋转图形的特征,三角形ABC绕点A旋转90°后,点A的位置不动,其余各部分均绕点A按相同的方向,旋转相同的度数,即可三角形ABC绕点A按逆时针方向旋转90°后得到的图形①、②、③.
30.见详解
【分析】根据题目要求确定旋转中心(点B)、旋转方向(顺时针)、旋转角度(90°),分析所作图形可知,将此线段绕B点顺时针旋转90°即可,线段AB的长度为3个小格,则旋转后的线段长度也为3个小格,依此画图即可。
【详解】画图如下:
31.(1)(2)(3)见详解
【分析】(1)根据旋转的特征,图形A绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线L)的右边画出图形A的关键对称点,依次连接、涂色即可作图形A的轴对称图形C;根据平移的特征,把图形C的各顶点分别向右平移4格,依次连接、涂色即可得到平移后的图形D。
(3)根据图形放大的意义,把图形E的长、宽均放大到原来的2倍所得到的长方形就是原图形按2∶1放大后的图形F。
【详解】根据题意画图如下:
32.见详解
【分析】先将380千米化成38000000厘米,然后根据比例尺=图上距离∶实际距离,计算出图上距离,然后在合适位置画出空间站距离地面的位置即可。
【详解】380千米=38000000厘米
38000000÷20000000=1.9(厘米)
则画图如下:
33.见详解
【分析】根据旋转的特征,梯形绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点,按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】
【点睛】本题考查如何画旋转后的图形,旋转三要素是:旋转中心、旋转方向、旋转角度。
34.见详解
【分析】可以根据所学到的简单的几何图形,先在左上角的正方形内画出两个交叉的四边形,根据平移的特点,把四边形向右平移到右边的正方形内,再用左上角正方形内两个交叉的四边形向先平移到左下角正方形内,再把左下角内两个交叉的四边形向右边右下角正方形内平移,即可得到一个图案(答案不唯一)。
【详解】
【点睛】本题主要是考查利用一个简单图形通过平移设计图案,考查学生的创新意识。
35.见详解
【分析】画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接,据此作图。
【详解】根据分析画图如下:
【点睛】本题主要考查作旋转后的图形,解题时注意旋转方向与角度。
36.如下图:
【详解】根据题意可知,经过旋转,图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等,图形旋转要注意四要素:原位置、旋转中心、旋转方向、旋转角,据此作图.
37.
【详解】(I)轴对称图形的定义是:一个图形沿某条直线对折后,直线两旁的部分能够完全重合,这个图形就是轴对称图形,由此即可画出图形(I)的另一半,使它成为一个轴对称图形;(II)根据图形旋转的方法,先把与点O相连的两条边逆时针旋转90°,即可画出旋转后的图形;(III)根据图形的放大与缩小的方法,将这个图(III)长方形的长、宽各扩大3倍即可画出这个符合题意的图形
38.
【详解】略
39.见详解
【分析】(1)看清平移的方向和距离,画出平移后的图形即可;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可;
(3)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(4)将图③的底和高同时缩小到原来的,画出缩小后的图形。
【详解】如图:
【点睛】本题考查了图形的平移、画轴对称图形、旋转、图形的放大与缩小,关键是能准确画图。
40.
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版六年级下册数学期末专题训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
1.按要求画一画。
(1)以虚线MN为对称轴,画出图形A的轴对称图形B。
(2)将图形B绕点O逆时针旋转90°,得到图形C。
(3)将图形C向左平移6格,得到图形D。
2.自己按一定的规律设计一组图形,让同学来找一找规律。
3.如下图,剪纸是中华民族优秀的传统民间艺术之一,有很多的剪纸作品都可以看作是由一个基本图形经过平移、旋转或轴对称得到的(如下图)。你能设计这样一幅剪纸作品,并贴在下面吗?
4.按要求画一画。
(1)将图形①按1∶3缩小。
(2)将图形②按2∶1放大。
5.长方体的两个面如下图,请画出长方体的另外四个面。
6.把平行四边形各边缩小.
7.画出图形A绕点O顺时针旋转90°后的图形.
8.将图①绕点A顺时针旋转90°得到图②,再将图②向右平移5格后得到图③。
9.画出三角形绕点逆时针旋转90°后的图形。
10.国家“双减”政策实施后,从根本上减轻了学生的课业负担,更重视学生的实践创新发展。张老师给学生布置了实践作业,淘气和同学们想把长方形的乒乓球室的平面图绘制出来,它们测量乒乓球室长20m,宽8m,请你选择合适的比例尺,也在下面画出乒乓球室的平面图。
11.画出图中的图形绕点O逆时针旋转90°后得到的图形。
12.在下面的方格图中,画出一个长方形、平行四边形和梯形。
13.画出线段AB绕点A顺时针旋转90°后的线段。
14.三角形ABC是将原图形向上平移2格,再向右平移8格后得到的。请画出平移前的图形,再画出将三角形ABC绕C点逆时针旋转180°后得到的图形。
15.按的比画出长方形放大后的图形。
16.画一画。
(1)将长方形按放大,画出放大后的图形。
(2)将梯形绕点O逆时针旋转90°,画出旋转后的图形。
(3)画一个三角形和一个平行四边形,使它们的面积相等。
17.按3:1画出下图中三角形放大后的图形。
18.把所给图形先绕O点顺时针旋转90度得到图B,图B再向右平移4格得到图D。
19.根据要求在图中操作。
①画出把三角形向左平移5格后的图形。
②画出把三角形绕C点顺时针旋转90°后的图形。
③如果1个小方格表示1平方厘米,在方格纸上设计一个面积是8平方厘米的轴对称图,并画出对称轴。
20.放大与缩小。
(1)按3∶1的比画出图①放大后的图形。
(2)按1∶2的比画出图②缩小后的图形。
21.画出你的书房是平面图。
22.在下图中,分别画出猴子在A,B位置时所能看到的范围。
23.(1)以直线xy为对称轴作图A的轴对称图形得到图B。
(2)将图B绕O点,顺时针旋转90°,得到图C。
(3)将图C向左平移7个格,得到图D。
24.画出这面小旗绕O点顺时针旋转90°后向左平移3格后得到的图形.
25.按要求画一画。
(1)画出图形A绕点O顺时针旋转90°后得到的图形B。
(2)画出图形B向右平移9格后得到的图形C。
26.画出房子的另一半。
27.将下面的正方形放大,使放大后的图形与原图形对应线段长的比为4∶1。
28.画出图形A关于直线l的轴对称图形,然后让新图绕o’点旋转900,连续旋转三次的图形.
29.在方格内按要求操作.
(i)把梯形按3:1放大,画出放大后的图形.
(ii)把三角形绕A点按逆时针方向连续旋转3次,每次都旋转 90° ,画出每次旋转后的图形,并标上序号①、②、③.
30.画出线段AB绕点B顺时针旋转90°后的线段。
31.按要求在方格纸上画图。
(1)将图形A绕O点逆时针旋转90°得到图形B。
(2)以直线L为对称轴作图形A的轴对称图形C,再将图形C向右平移4格得到图形D。
(3)画出图形E按2∶1放大后的图形F。
32.2022年6月5日10时44分,“神舟十四号”载人飞船开启了“天宫”空间站的新纪元,距地380千米高度的“天宫”空间站即将成型,我国的载人航天事业将正式进入“空间站”时代。请在下图中画出我国空间站距离地面的位置。
33.画出梯形绕点“O”逆时针旋转90°后得到的图形。
34.请你利用“图形运动”的相关知识,在如图的方格中自己设计一个图案,并把你设计图案时使用的图形的运动方式写出来。
35.画出图形ABCED绕A点顺时针旋转90°后的图形,并标出C点旋转后的位置C′点。
36.按要求画一画.
(1)把梯形绕A点顺时针旋转90°.
(2)把三角形绕B点逆时针旋转90°.
37.按要求操作.
(I)画出图(I)的另一半,使它成为一个轴对称图形.
(II)把图(II)绕O点逆时针旋转90°.
(III)把图(3)按3:1的比放大.
38.画出下面的线段AB绕点C顺时针旋转90°后的图形.
39.按要求在方格纸上画一画。
(1)将图①先向右平移8格,再向下平移3格
(2)以虚线MN为对称轴,画出图②的轴对称图形的另一半。
(3)将图③绕点O逆时针旋转
(4)将图③缩小,使得缩小后的图形与原图形对应线段长的比是1∶2。
40.王杰和同学测量了他们学校的一些主要建筑的长和宽以及方位,你能根据这些数据将这些建筑物在平面图上标出来吗?
教学楼在校门的正北方向150米处,教学楼长100米,宽60米。图书馆在校门的北偏东45度方向150米处,图书馆长60米,宽20米。体育馆在校门的西偏北40度方向200米处,体育馆长150米,宽100米。操场在校门的东偏北15度方向50米处,操场长200米,宽150米。
《北师大版六年级下册数学期末专题训练:作图题》参考答案
1.见详解
【分析】(1)根据轴对称图形的特征,各对称点到对称轴的距离相等,据此先描出各对称点的位置,然后顺次连接格点即可画出图形A的轴对称图形B;
(2)根据旋转的特征,将图形B绕点O逆时针旋转90°,点O的位置不变,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形C;
(3)根据平移的特征,将图形C各顶点向左平移6格,即可画出平移后的图形D。
【详解】画图如下:
【点睛】本题考查的目的是理解掌握图形的平移、旋转以及轴对称的性质及应用。
2.如图所示:
【详解】这个图形就是一个梯形旋转四次设计出的图形。
3.见详解
【分析】由给出的这两个图形可知,它们都是轴对称图形,都可以找到对称轴,再根据对称轴剪图形。因此要设计一幅剪纸作品,先找出对称轴,想象图形形状,再动手剪,最后摊开图形即可完成。
【详解】答案不唯一,满足条件即可,如图所示:
4.见详解
【分析】假设每个方格的边长为1,
(1)原梯形的上底、下底、高分别是6、3、6,缩小后是2、1、2。
(2)原三角形的两条直角边是2和4,扩大后分别是4和8。
【详解】(1)(2)如图:
【点睛】理解缩小与扩大的意义与方法是解决本题的关键。
5.见详解
【分析】长方体的特征:长方体有6个面,有三组相对的面完全相同,一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。
图中已知长方体的两个面分别是6×3、4×3的长方形,那么还各有一个6×3、4×3的长方形,另外有两个6×4的长方形,据此画出这四个面。
有两个相同的面
【详解】如图:
6.
【详解】各边都缩小,那么底边是4格,高是2格,由此画出缩小后的平行四边形即可.
7.
【详解】略
8.见详解
【分析】点A不动,将图形的各点绕着点A顺时针旋转90°,然后顺次连接各点,画出旋转后的图形;
将旋转后的图形各个顶点均向右平移5格,找出对应点,再依次连接,画出平移后的图形。
【详解】如图:
9.见详解
【分析】图形的旋转要满足三个条件:第一要找出图形旋转时所绕的旋转点;二要判断清楚图形的旋转方向;三是确定图形的旋转角度;在本题中,三角形是绕点O逆时针旋转90°。据此解答即可。
【详解】
【点睛】本题主要考查了旋转图形的画法,要画图形进行旋转后的图形,一定要找出图形的旋转点,旋转方向和旋转角度。
10.见详解
【分析】可以按照比例尺1∶400画出平面图。也就是图上1厘米的距离等于实际距离的400厘米。1m=100cm,高级单位转化为低级单位用乘法,则20m=2000cm,图上的距离用2000÷400=5(cm),8m=800cm,800÷400=2(cm)。再用有刻度的直尺画出平面图。
【详解】用比例尺为1∶400画图。
11.见详解
【分析】根据旋转的方法,将三角形与点O相连的边绕点O逆时针旋转90度,再将其它边连起来即可。
【详解】如图:
【点睛】做旋转后的图形时,一定要注意旋转的方向和角度,图形的大小和形状不变。
12.见详解
【分析】长方形的特征是两组对边分别平行、四个角都是直角的四边形。
平行四边形的特征是两组对边互相平行且相等。
梯形是只有一组对边互相平行的四边形;据此画图。
【详解】如图:
(画法不唯一)
13.见详解
【分析】根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°),找出点B的对应点B’,连接AB’,据此作图。
【详解】作图如下:
14.见详解
【分析】把三角形ABC按原路返回,返回时平移的方向相反,距离不变。根据平移的特征把三角形ABC的各顶点分别向左平移8格,再向下平移2格,依次连接即可得到平移前的图形;根据旋转的特征,三角形ABC绕点C逆时针旋转180°,点C的位置不动,这个图形的各部分均绕此点按逆时针方向旋转180°即可画出旋转后的图形。
【详解】根据题意画图如下:
15.见详解
【分析】根据图可知,这个长方形的长是3格,宽是2格,按2∶1的比扩大长方形,则长方形的长和宽都扩大到原来的2倍,此时的长是:3×2=6(格),宽:2×2=4(格),据此画图即可。
【详解】由分析可知:如下图所示:
【点睛】本题主要考查图形的放大,要注意是图形每条边都放大相应的倍数。
16.见详解
【分析】(1)将长方形的长和宽均放大到原来的2倍,画出放大后的图形;
(2)点O不动,将梯形的各边均逆时针旋转90°,画出旋转后的图形;
(3)三角形面积=底×高÷2,平行四边形面积=底×高,那么可以取三角形底为4,高为2,面积为4×2÷2=4,取平行四边形底为4,高为1,面积为4×1=4。此时,画出的三角形和平行四边形的面积相等。
【详解】如图:
(三角形和平行四边形的画法不唯一)
17.
【详解】略
18.见详解
【分析】(1)根据旋转的意义,图形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕点O按相同的方向旋转相同的度数,即可画出旋转后的图形B;
(2)根据图形平移的特征,把图形B的各顶点分别向右平移4格,再依次连接即可得到平移后的图形D。
【详解】
【点睛】本题考查了旋转和平移的意义,明确旋转和平移的定义是作图的关键。
19.见详解
【分析】①根据平移图形的特征,把△ABC的三个顶点分别向左平移5格,得到三个对应点A′B′C′,首尾连接这三点所得到的△A′B′C′就是△ABC的三个顶点分别向左平移5格得到的图形。
②根据旋转图形的特征,把△A′B′C′绕C′点顺时针旋转90°,C′点不动,△A′B′C′各边均绕C′点顺时针旋转90°,即A′C′旋转到A″C′的位置,B′C′旋转到B″C′R 的位置,连接A″B″,△A″B″C′就是△A′B′C′绕C′点顺时针旋转90°后的图形。
③画一个长是4厘米,宽是2厘米的长方形就是一个面积为8平方厘米的轴对称图形(答案不唯一)。
【详解】画图如下:
【点睛】本题是考查作图形的平移、旋转及轴对称图形,掌握图形的平移、旋转以及画轴对称图形的方法是解题的关键。
20.见详解
【分析】(1)根据图形放大的意义,把图形的上、下底及高均放大到原来的3倍,对应角大小不变,所得到的图形就是原图形按3∶1放大后的图形。
(2)根据图形缩小的意义,把平行四边形的各边均缩小到原来的,对应角大小不变,所得到的图形就是原图形按1∶2缩小后的图形。
【详解】(1)(2)如图:
【点睛】图形放大或缩小指对应边(线段)放大或缩小,对应角大小不变,即图形放大或缩小后,改变的是大小,形状不变。
21.
【详解】画平面图的时候,先要测量并记录数据,然后再确定以多大的比例画图,最后根据比例手工绘制样图。(答案不唯一)
22.见详解
【分析】观测点越高,观察的范围越大,观察点越低,观察的范围越小,随着观测点的变化观察范围也在变化。据此画出A、B两地和围墙外最高点连线交地平面即可。
【详解】如图:
23.(1)见详解;(2)见详解;(3)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点,依次连接即可;
(2)根据旋转的特征,图B绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图C;
(3)根据平移的特征,把图C的各顶点分别向左平移7个格,依次连接即可得到平移后的图D。
【详解】如图:
【点睛】此题是考查了图形的平移、旋转以及作轴对称图形,要掌握相关知识点。
24.
【详解】本题考查平移和旋转的相关知识,将简单图形平移或旋转一定的度数.
25.(1)(2)见详解
【分析】(1)根据旋转的特征,图形A绕点O顺时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形B。
(2)根据平移的特征,把图形B的各顶点分别向右平移9格,依次连接即可得到平移后的图形。
【详解】
【点睛】图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。图形平移注意三要素:即原位置、平移方向、平移距离。
26.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
27.见详解
【分析】把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1。
【详解】
28.
【详解】略
29.(i)梯形按3:1放大后的图形如图红色部分;
(ii) 三角形绕A点按逆时针方向连续旋转3次的图形如图①、②、③
【分析】①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.
【详解】(1)按3:1的比例画出梯形放大后的图形,就是把原梯形的上底、下底和高分别扩大到原来的3倍,原梯形的上底、下底和高分别是2格、3格和1格,扩大后的梯形的上底、下底和高分别是6格、9格和3格.
(2)根据旋转图形的特征,三角形ABC绕点A旋转90°后,点A的位置不动,其余各部分均绕点A按相同的方向,旋转相同的度数,即可三角形ABC绕点A按逆时针方向旋转90°后得到的图形①、②、③.
30.见详解
【分析】根据题目要求确定旋转中心(点B)、旋转方向(顺时针)、旋转角度(90°),分析所作图形可知,将此线段绕B点顺时针旋转90°即可,线段AB的长度为3个小格,则旋转后的线段长度也为3个小格,依此画图即可。
【详解】画图如下:
31.(1)(2)(3)见详解
【分析】(1)根据旋转的特征,图形A绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线L)的右边画出图形A的关键对称点,依次连接、涂色即可作图形A的轴对称图形C;根据平移的特征,把图形C的各顶点分别向右平移4格,依次连接、涂色即可得到平移后的图形D。
(3)根据图形放大的意义,把图形E的长、宽均放大到原来的2倍所得到的长方形就是原图形按2∶1放大后的图形F。
【详解】根据题意画图如下:
32.见详解
【分析】先将380千米化成38000000厘米,然后根据比例尺=图上距离∶实际距离,计算出图上距离,然后在合适位置画出空间站距离地面的位置即可。
【详解】380千米=38000000厘米
38000000÷20000000=1.9(厘米)
则画图如下:
33.见详解
【分析】根据旋转的特征,梯形绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点,按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】
【点睛】本题考查如何画旋转后的图形,旋转三要素是:旋转中心、旋转方向、旋转角度。
34.见详解
【分析】可以根据所学到的简单的几何图形,先在左上角的正方形内画出两个交叉的四边形,根据平移的特点,把四边形向右平移到右边的正方形内,再用左上角正方形内两个交叉的四边形向先平移到左下角正方形内,再把左下角内两个交叉的四边形向右边右下角正方形内平移,即可得到一个图案(答案不唯一)。
【详解】
【点睛】本题主要是考查利用一个简单图形通过平移设计图案,考查学生的创新意识。
35.见详解
【分析】画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接,据此作图。
【详解】根据分析画图如下:
【点睛】本题主要考查作旋转后的图形,解题时注意旋转方向与角度。
36.如下图:
【详解】根据题意可知,经过旋转,图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等,图形旋转要注意四要素:原位置、旋转中心、旋转方向、旋转角,据此作图.
37.
【详解】(I)轴对称图形的定义是:一个图形沿某条直线对折后,直线两旁的部分能够完全重合,这个图形就是轴对称图形,由此即可画出图形(I)的另一半,使它成为一个轴对称图形;(II)根据图形旋转的方法,先把与点O相连的两条边逆时针旋转90°,即可画出旋转后的图形;(III)根据图形的放大与缩小的方法,将这个图(III)长方形的长、宽各扩大3倍即可画出这个符合题意的图形
38.
【详解】略
39.见详解
【分析】(1)看清平移的方向和距离,画出平移后的图形即可;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可;
(3)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(4)将图③的底和高同时缩小到原来的,画出缩小后的图形。
【详解】如图:
【点睛】本题考查了图形的平移、画轴对称图形、旋转、图形的放大与缩小,关键是能准确画图。
40.
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
