期末计算题专项训练(含解析)-2024-2025学年数学五年级下册北师大版
文档属性
| 名称 | 期末计算题专项训练(含解析)-2024-2025学年数学五年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 923.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 19:31:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末计算题专项训练-2024-2025学年数学五年级下册北师大版
1.计算下面各题,能简算的要简算。
2.观察数据特点,用适当的方法计算。
3.观察数据特点,用适当的方法计算。
4.选择合适的方法计算。
5.计算下列各题。
6.脱式计算。(能简算的要简算)
7.计算下面各题,能简算的要简算。
8.用自己喜欢的方法计算下面各题。
12-- -+- -(-)
9.计算下面各题,怎样简便就怎样计算。
10.计算下列各题,能简算的要简算。
-+ 2--
× ÷40
11.脱式计算。
12.计算下面各题,能简算的要简算。
-(+) --
××24 ÷+×15
13.解方程。
(1) (2) (3)
14.解方程。
15.解方程。
(1) (2) (3)
16.解方程。
y+y=29
17.求正方体的体积。
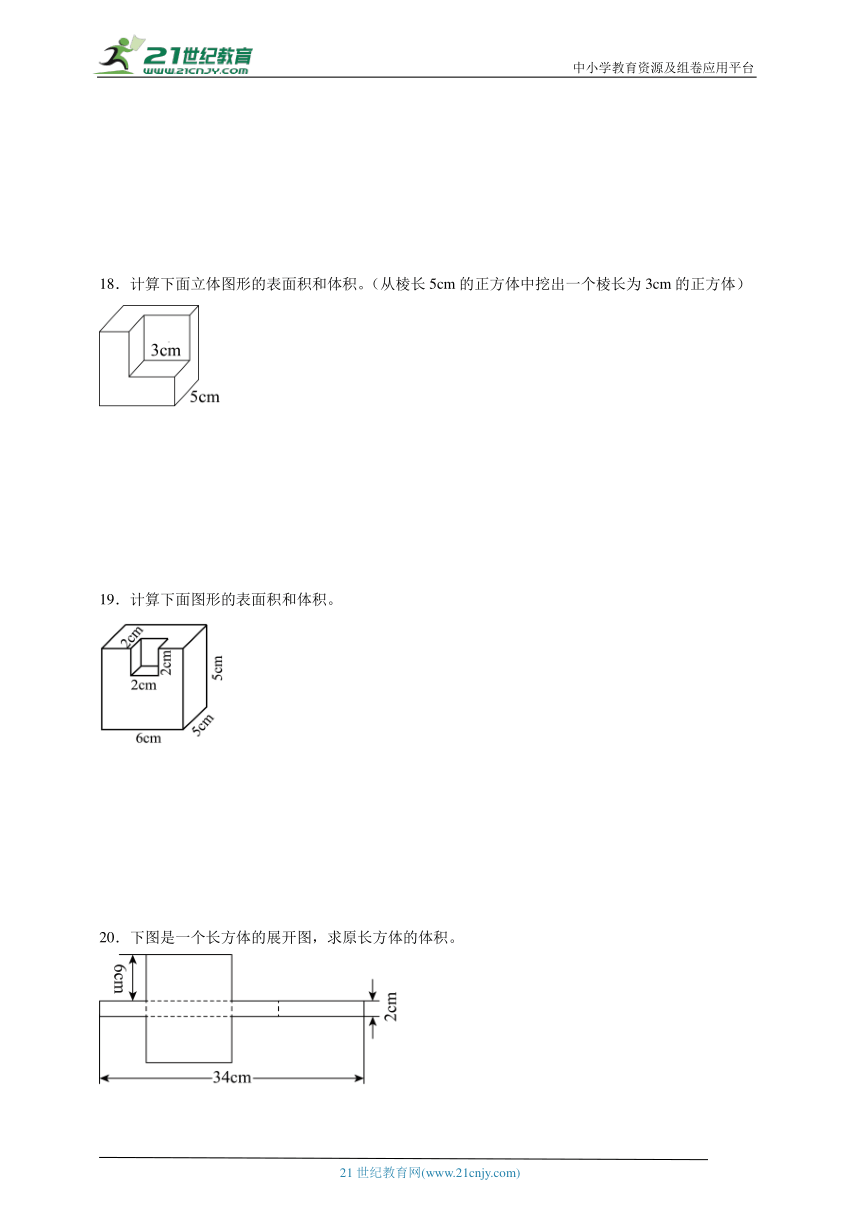
18.计算下面立体图形的表面积和体积。(从棱长5cm的正方体中挖出一个棱长为3cm的正方体)
19.计算下面图形的表面积和体积。
20.下图是一个长方体的展开图,求原长方体的体积。
21.计算下面图形的表面积和体积。(单位:dm)
22.求下面图形的体积。
23.求出下面图形的表面积和体积。
24.求下面图形的表面积和体积。
《期末计算题专项训练-2024-2025学年数学五年级下册北师大版》参考答案
1.;;2
【分析】分数与分数的乘法:分子乘分子的积作为积的分子,分母乘分母的积作为积的分母,能约分的先进行约分;
运用加法交换律进行简便计算即可;
运用加法交换律和加法结合律进行简便计算即可。
【详解】
2.;1;
【分析】“”先通分,将分母都化成12,再计算;
“”同级运算,先带符号交换和的位置,再根据减法的性质计算。减法的性质:连续减去两个数,就等于减去这两个数的和;
“”根据减法的性质去括号,再带符号交换和的位置,再计算。
【详解】
=
=
=
=
=
=
=1
=
=
=
=
3.;
;2
【分析】+(-),去掉括号,原式化为:+-,再进行计算。
-+,根据加法交换律,原式化为:+-,再进行计算。
--,根据减法性质,原式化为:-(+),再进行计算。
(+)+(+),去掉括号,原式化为:+++,再根据加法交换律,原式化为:+++,再根据加法结合律,原式化为:(+)+(+),再进行计算。
【详解】+(-)
=+-
=1-
=
-+
=+-
=1-
=
--
=-(+)
=-1
=
(+)+(+)
=+++
=+++
=(+)+(+)
=1+1
=2
4.;;;4
【分析】(1)利用加法交换律进行简便计算;
(2)先算加法,再算减法,从左往右依次计算;
(3)先去括号,括号前是减号,括号内符号要变号,再从左往右依次计算即可;
(4)利用减法的性质进行简便计算即可。
【详解】
5.;;
【分析】分数四则混合运算和整数四则混合运算顺序相同,有加减和乘除,先算乘除后算加减,有括号先算括号里面的,按照从左往右的顺序依次计算。异分母分数相加减,要先通分成同分母分数,按照同分母分数加减法进行计算。
【详解】
6.;
【分析】(1)根据加法交换律交换与的位置,再去掉小括号,去掉小括号时括号里面的加号变减号,再进行计算即可;
(2)先去掉小括号,去掉小括号后括号里面的加号变减号,再算除法,最后根据异分母分数减法的方法计算。
【详解】
=
=
=1-
=
=
=
=
=
=
=
7.;;
【分析】应用加法结合律先计算分母是13的两个同分母分数的和,再与第一个分数相加求和;
12、3、8的最小公倍数是24,一次性通分后再从左往右依次计算;
应用减法的性质,用第一个分数减去后两个分数的和。
【详解】
8.11;0;
【分析】(1)根据减法的性质a-b-c=a-(b+c)进行简算;
(2)先交换“-”和“+”的位置,再根据加法结合律(a+b)+c=a+(b+c),减法的性质a-b-c=a-(b+c)进行简算;
(3)先算括号里面的减法,再算括号外面的减法。
【详解】(1)12--
=12-(+)
=12-1
=11
(2)-+-
=+--
=(+)-(+)
=1-1
=0
(3)-(-)
=-(-)
=-
=-
=
9.;8;
【分析】(1)根据“带着符号搬家”的方法,把原式改写为,再根据减法的性质a-b-c=a-(b+c),把式子改为简算;
(2)先把除法改写成乘法,再运用乘法交换律简算;
(3)根据减法的性质a-(b-c)=a+c-b,原式改写为简算。
【详解】
=
=
=1-
=
=
=
=1×8
=8
=
=1-
=
10.;1
;
【分析】(1)同级运算,从左向右进行计算;
(2)运用减法的性质:连续减去两个数,相当于减去它们的和,进行简便计算;
(3)按照分数乘法的计算方法计算即可;
(4)根据除以一个不为0的数,相当于乘这个数的倒数,把除法改成乘法,再按照分数乘法的计算方法计算。
【详解】(1)-+
=+
=
(2)2--
=2-(+)
=2-1
=1
(3)×
=
=
(4)÷40
=×
=
11.;;
20;;
【分析】(1)按照从左到右的运算顺序进行计算即可;
(2)化除法为乘法,然后运用乘法交换律进行计算即可;
(3)按照从左到右的运算顺序进行计算即可;
(4)先算小括号里面的除法,再算括号外面的乘法;
(5)先算小括号里面的除法,再算括号外面的除法;
(6)先算小括号里面的乘法,再算括号外面的除法。
【详解】
=
=
=
=
=
=
=
=
=
=
=20
=
=
=
=
=
12.;
;15
【分析】(1)先算小括号里面的加法,再算括号外的减法;
(2)根据减法的性质,先算+,再算减法;
(3)根据乘法结合律,先运算×24,再用乘它们的乘积;
(4)先把除以改写成乘15,再根据乘法分配律简算。
【详解】-(+)
=-(+)
=-
=-
=
--
=-(+)
=-1
=
××24
=×3
=
÷+×15
=×15+×15
=(+)×15
=1×15
=15
13.(1);(2);(3)
【分析】(1)根据等式的性质1,将方程左右两边同时加上即可;
(2)根据等式的性质1,将方程左右两边同时减去即可;
(3)根据等式的性质2,将方程左右两边同时乘即可。
【详解】(1)
解:
(2)
解:
(3)
解:
14.;;;
【分析】方程两边同时除以3解出未知数;
方程两边同时除以解出未知数;
方程两边同时除以解出未知数;
方程两边同时除以解出未知数,据此解答。
【详解】
解:
解:
解:
解:
15.(1);(2);(3)
【分析】(1)根据等式的性质,方程两边同时除以即可;
(2)根据等式的性质,方程两边同时乘即可;
(3)根据等式的性质,方程两边同时乘,再同时除以即可。
【详解】(1)
解:
(2)
解:
(3)
解:
16.x=;y=35
【分析】先把方程的左右两边同时减去,再同时除以即可;
先把方程的左边相加,再把方程的左右两边同时除以()的和即可。
【详解】x+=
解:x+-=
x=-
x=
x÷=
x=×
x=
y+y=29
解:()y=29
(+)y=29
y=29
y÷=29÷
y=29×
y=35
17.125dm3
【分析】根据正方体体积=边长×边长×边长,代入数据,即可解答。
【详解】5×5×5
=25×5
=125(dm3)
正方体体积是125dm3。
18.表面积:150cm2;体积:98cm3
【分析】从图中可知,大正方体的右上角挖去一个小正方体,露出3个面,这3个面可以向外平移,正好补齐缺口,所以这个立体图形的表面积=大正方体的表面积,根据正方体的表面积公式S=6a2,代入数据计算,求出立体图形的表面积。
立体图形的体积=大正方体的体积-小正方体的体积,根据正方体的体积公式V=a3,代入数据计算,求出立体图形的体积。
【详解】表面积:
5×5×6
=25×6
=150(cm2)
体积:
5×5×5-3×3×3
=125-27
=98(cm3)
立体图形的表面积是150cm2,体积是98cm3。
19.178;142
【分析】图形的表面积等于长是6cm、宽是5cm、高是5cm的长方体的表面积加上边长为2cm的两个正方形的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方形的面积=边长×边长,代入数据计算即可;
图形的体积等于长是6cm、宽是5cm、高是5cm的长方体的体积减去棱长是2cm的正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】(6×5+6×5+5×5)×2+2×2×2
=(30+30+25)×2+4×2
=(60+25)×2+8
=85×2+8
=170+8
=178()
6×5×5-2×2×2
=30×5-4×2
=150-8
=142()
20.132cm3
【分析】观察长方体的展开图,原长方体的长=(34-6×2)÷2cm,长方体的宽6cm,长方体的高2cm,根据长方体体积=长×宽×高,列式计算即可。
【详解】(34-6×2)÷2
=(34-12)÷2
=22÷2
=11(cm)
11×6×2=132(cm3)
原长方体的体积是132cm3。
21.表面积为198,体积为149。
【分析】观察图形可知,下方是一个棱长为5dm的正方体,上方是一个长2dm、宽2dm、高为6dm的长方体,将长方体放在正方体的上面。先根据表面积的公式:长方体的表面积=(长×宽+长×高+宽×高)×2,正方体表面积=棱长×棱长×6可得,整个图形的表面积比两个图形的表面积之和减少了2个正方形的面积,那么用长方体和正方体的表面积之和,减去2个正方形的面积。再根据体积的公式:长方体的体积=长×宽×高,正方体体积=棱长×棱长×棱长可得,用长方体的体积加上正方体的体积即可求出整个图形的体积;据此计算即可。
【详解】正方体表面积:5×5×6
=25×6
=150()
长方体表面积:(2×2+2×6+2×6)×2
=(4+12+12)×2
=(16+12)×2
=28×2
=56()
150+56-2×2×2
=150+56-4×2
=150+56-8
=206-8
=198()
正方体体积:5×5×5
=25×5
=125()
长方体体积:2×2×6
=4×6
=24()
125+24=149()
答:该图形的表面积为198,体积为149。
22.12.5cm3;40cm3;480dm3
【分析】
根据长方体的体积=长×宽×高=底面积×高,代入数据解答即可。
【详解】
左图:6.25×2=12.5(cm3)
第一个的体积是12.5cm3。
中间:25×1.6=40(cm3)
第二个的体积是40cm3。
右图:96×5=480(dm3)
第三个的体积是480dm3。
23.表面积:260cm2;体积:219cm3
【分析】表面积=长是8cm,宽是8cm,高是3cm的长方体的表面积+棱长是3cm的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;正方体侧面积公式:棱长×棱长×4,代入数据,即可解答。
体积=长是8cm,宽是8cm,高是3cm的长方体的体积+棱长是3cm的正方体的体积;根据长方体的体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:(8×8+8×3+8×3)×2+3×3×4
=(64+24+24)×2+9×4
=(88+24)×2+36
=112×2+36
=224+36
=260(cm2)
体积:8×8×3+3×3×3
=64×3+9×3
=192+27
=219(cm3)
24.表面积:246cm2;体积:190cm3
【分析】组合体的表面积=左边长方体的表面积+右边长方体上、下、前、后四个面的面积;
组合体的体积=两个长方体的体积和;据此解答。
【详解】表面积:(4×6+5×6+4×5)×2+(7×2+5×7)×2
=(24+30+20)×2+(14+35)×2
=148+98
=246(平方厘米)
体积:4×5×6+7×5×2
=120+70
=190(立方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末计算题专项训练-2024-2025学年数学五年级下册北师大版
1.计算下面各题,能简算的要简算。
2.观察数据特点,用适当的方法计算。
3.观察数据特点,用适当的方法计算。
4.选择合适的方法计算。
5.计算下列各题。
6.脱式计算。(能简算的要简算)
7.计算下面各题,能简算的要简算。
8.用自己喜欢的方法计算下面各题。
12-- -+- -(-)
9.计算下面各题,怎样简便就怎样计算。
10.计算下列各题,能简算的要简算。
-+ 2--
× ÷40
11.脱式计算。
12.计算下面各题,能简算的要简算。
-(+) --
××24 ÷+×15
13.解方程。
(1) (2) (3)
14.解方程。
15.解方程。
(1) (2) (3)
16.解方程。
y+y=29
17.求正方体的体积。
18.计算下面立体图形的表面积和体积。(从棱长5cm的正方体中挖出一个棱长为3cm的正方体)
19.计算下面图形的表面积和体积。
20.下图是一个长方体的展开图,求原长方体的体积。
21.计算下面图形的表面积和体积。(单位:dm)
22.求下面图形的体积。
23.求出下面图形的表面积和体积。
24.求下面图形的表面积和体积。
《期末计算题专项训练-2024-2025学年数学五年级下册北师大版》参考答案
1.;;2
【分析】分数与分数的乘法:分子乘分子的积作为积的分子,分母乘分母的积作为积的分母,能约分的先进行约分;
运用加法交换律进行简便计算即可;
运用加法交换律和加法结合律进行简便计算即可。
【详解】
2.;1;
【分析】“”先通分,将分母都化成12,再计算;
“”同级运算,先带符号交换和的位置,再根据减法的性质计算。减法的性质:连续减去两个数,就等于减去这两个数的和;
“”根据减法的性质去括号,再带符号交换和的位置,再计算。
【详解】
=
=
=
=
=
=
=1
=
=
=
=
3.;
;2
【分析】+(-),去掉括号,原式化为:+-,再进行计算。
-+,根据加法交换律,原式化为:+-,再进行计算。
--,根据减法性质,原式化为:-(+),再进行计算。
(+)+(+),去掉括号,原式化为:+++,再根据加法交换律,原式化为:+++,再根据加法结合律,原式化为:(+)+(+),再进行计算。
【详解】+(-)
=+-
=1-
=
-+
=+-
=1-
=
--
=-(+)
=-1
=
(+)+(+)
=+++
=+++
=(+)+(+)
=1+1
=2
4.;;;4
【分析】(1)利用加法交换律进行简便计算;
(2)先算加法,再算减法,从左往右依次计算;
(3)先去括号,括号前是减号,括号内符号要变号,再从左往右依次计算即可;
(4)利用减法的性质进行简便计算即可。
【详解】
5.;;
【分析】分数四则混合运算和整数四则混合运算顺序相同,有加减和乘除,先算乘除后算加减,有括号先算括号里面的,按照从左往右的顺序依次计算。异分母分数相加减,要先通分成同分母分数,按照同分母分数加减法进行计算。
【详解】
6.;
【分析】(1)根据加法交换律交换与的位置,再去掉小括号,去掉小括号时括号里面的加号变减号,再进行计算即可;
(2)先去掉小括号,去掉小括号后括号里面的加号变减号,再算除法,最后根据异分母分数减法的方法计算。
【详解】
=
=
=1-
=
=
=
=
=
=
=
7.;;
【分析】应用加法结合律先计算分母是13的两个同分母分数的和,再与第一个分数相加求和;
12、3、8的最小公倍数是24,一次性通分后再从左往右依次计算;
应用减法的性质,用第一个分数减去后两个分数的和。
【详解】
8.11;0;
【分析】(1)根据减法的性质a-b-c=a-(b+c)进行简算;
(2)先交换“-”和“+”的位置,再根据加法结合律(a+b)+c=a+(b+c),减法的性质a-b-c=a-(b+c)进行简算;
(3)先算括号里面的减法,再算括号外面的减法。
【详解】(1)12--
=12-(+)
=12-1
=11
(2)-+-
=+--
=(+)-(+)
=1-1
=0
(3)-(-)
=-(-)
=-
=-
=
9.;8;
【分析】(1)根据“带着符号搬家”的方法,把原式改写为,再根据减法的性质a-b-c=a-(b+c),把式子改为简算;
(2)先把除法改写成乘法,再运用乘法交换律简算;
(3)根据减法的性质a-(b-c)=a+c-b,原式改写为简算。
【详解】
=
=
=1-
=
=
=
=1×8
=8
=
=1-
=
10.;1
;
【分析】(1)同级运算,从左向右进行计算;
(2)运用减法的性质:连续减去两个数,相当于减去它们的和,进行简便计算;
(3)按照分数乘法的计算方法计算即可;
(4)根据除以一个不为0的数,相当于乘这个数的倒数,把除法改成乘法,再按照分数乘法的计算方法计算。
【详解】(1)-+
=+
=
(2)2--
=2-(+)
=2-1
=1
(3)×
=
=
(4)÷40
=×
=
11.;;
20;;
【分析】(1)按照从左到右的运算顺序进行计算即可;
(2)化除法为乘法,然后运用乘法交换律进行计算即可;
(3)按照从左到右的运算顺序进行计算即可;
(4)先算小括号里面的除法,再算括号外面的乘法;
(5)先算小括号里面的除法,再算括号外面的除法;
(6)先算小括号里面的乘法,再算括号外面的除法。
【详解】
=
=
=
=
=
=
=
=
=
=
=20
=
=
=
=
=
12.;
;15
【分析】(1)先算小括号里面的加法,再算括号外的减法;
(2)根据减法的性质,先算+,再算减法;
(3)根据乘法结合律,先运算×24,再用乘它们的乘积;
(4)先把除以改写成乘15,再根据乘法分配律简算。
【详解】-(+)
=-(+)
=-
=-
=
--
=-(+)
=-1
=
××24
=×3
=
÷+×15
=×15+×15
=(+)×15
=1×15
=15
13.(1);(2);(3)
【分析】(1)根据等式的性质1,将方程左右两边同时加上即可;
(2)根据等式的性质1,将方程左右两边同时减去即可;
(3)根据等式的性质2,将方程左右两边同时乘即可。
【详解】(1)
解:
(2)
解:
(3)
解:
14.;;;
【分析】方程两边同时除以3解出未知数;
方程两边同时除以解出未知数;
方程两边同时除以解出未知数;
方程两边同时除以解出未知数,据此解答。
【详解】
解:
解:
解:
解:
15.(1);(2);(3)
【分析】(1)根据等式的性质,方程两边同时除以即可;
(2)根据等式的性质,方程两边同时乘即可;
(3)根据等式的性质,方程两边同时乘,再同时除以即可。
【详解】(1)
解:
(2)
解:
(3)
解:
16.x=;y=35
【分析】先把方程的左右两边同时减去,再同时除以即可;
先把方程的左边相加,再把方程的左右两边同时除以()的和即可。
【详解】x+=
解:x+-=
x=-
x=
x÷=
x=×
x=
y+y=29
解:()y=29
(+)y=29
y=29
y÷=29÷
y=29×
y=35
17.125dm3
【分析】根据正方体体积=边长×边长×边长,代入数据,即可解答。
【详解】5×5×5
=25×5
=125(dm3)
正方体体积是125dm3。
18.表面积:150cm2;体积:98cm3
【分析】从图中可知,大正方体的右上角挖去一个小正方体,露出3个面,这3个面可以向外平移,正好补齐缺口,所以这个立体图形的表面积=大正方体的表面积,根据正方体的表面积公式S=6a2,代入数据计算,求出立体图形的表面积。
立体图形的体积=大正方体的体积-小正方体的体积,根据正方体的体积公式V=a3,代入数据计算,求出立体图形的体积。
【详解】表面积:
5×5×6
=25×6
=150(cm2)
体积:
5×5×5-3×3×3
=125-27
=98(cm3)
立体图形的表面积是150cm2,体积是98cm3。
19.178;142
【分析】图形的表面积等于长是6cm、宽是5cm、高是5cm的长方体的表面积加上边长为2cm的两个正方形的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方形的面积=边长×边长,代入数据计算即可;
图形的体积等于长是6cm、宽是5cm、高是5cm的长方体的体积减去棱长是2cm的正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】(6×5+6×5+5×5)×2+2×2×2
=(30+30+25)×2+4×2
=(60+25)×2+8
=85×2+8
=170+8
=178()
6×5×5-2×2×2
=30×5-4×2
=150-8
=142()
20.132cm3
【分析】观察长方体的展开图,原长方体的长=(34-6×2)÷2cm,长方体的宽6cm,长方体的高2cm,根据长方体体积=长×宽×高,列式计算即可。
【详解】(34-6×2)÷2
=(34-12)÷2
=22÷2
=11(cm)
11×6×2=132(cm3)
原长方体的体积是132cm3。
21.表面积为198,体积为149。
【分析】观察图形可知,下方是一个棱长为5dm的正方体,上方是一个长2dm、宽2dm、高为6dm的长方体,将长方体放在正方体的上面。先根据表面积的公式:长方体的表面积=(长×宽+长×高+宽×高)×2,正方体表面积=棱长×棱长×6可得,整个图形的表面积比两个图形的表面积之和减少了2个正方形的面积,那么用长方体和正方体的表面积之和,减去2个正方形的面积。再根据体积的公式:长方体的体积=长×宽×高,正方体体积=棱长×棱长×棱长可得,用长方体的体积加上正方体的体积即可求出整个图形的体积;据此计算即可。
【详解】正方体表面积:5×5×6
=25×6
=150()
长方体表面积:(2×2+2×6+2×6)×2
=(4+12+12)×2
=(16+12)×2
=28×2
=56()
150+56-2×2×2
=150+56-4×2
=150+56-8
=206-8
=198()
正方体体积:5×5×5
=25×5
=125()
长方体体积:2×2×6
=4×6
=24()
125+24=149()
答:该图形的表面积为198,体积为149。
22.12.5cm3;40cm3;480dm3
【分析】
根据长方体的体积=长×宽×高=底面积×高,代入数据解答即可。
【详解】
左图:6.25×2=12.5(cm3)
第一个的体积是12.5cm3。
中间:25×1.6=40(cm3)
第二个的体积是40cm3。
右图:96×5=480(dm3)
第三个的体积是480dm3。
23.表面积:260cm2;体积:219cm3
【分析】表面积=长是8cm,宽是8cm,高是3cm的长方体的表面积+棱长是3cm的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;正方体侧面积公式:棱长×棱长×4,代入数据,即可解答。
体积=长是8cm,宽是8cm,高是3cm的长方体的体积+棱长是3cm的正方体的体积;根据长方体的体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:(8×8+8×3+8×3)×2+3×3×4
=(64+24+24)×2+9×4
=(88+24)×2+36
=112×2+36
=224+36
=260(cm2)
体积:8×8×3+3×3×3
=64×3+9×3
=192+27
=219(cm3)
24.表面积:246cm2;体积:190cm3
【分析】组合体的表面积=左边长方体的表面积+右边长方体上、下、前、后四个面的面积;
组合体的体积=两个长方体的体积和;据此解答。
【详解】表面积:(4×6+5×6+4×5)×2+(7×2+5×7)×2
=(24+30+20)×2+(14+35)×2
=148+98
=246(平方厘米)
体积:4×5×6+7×5×2
=120+70
=190(立方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
