期末计算题专项训练(含解析)-2024-2025学年数学五年级下册人教版
文档属性
| 名称 | 期末计算题专项训练(含解析)-2024-2025学年数学五年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 959.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 19:31:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末计算题专项训练-2024-2025学年数学五年级下册人教版
1.能简便的要简便运算。
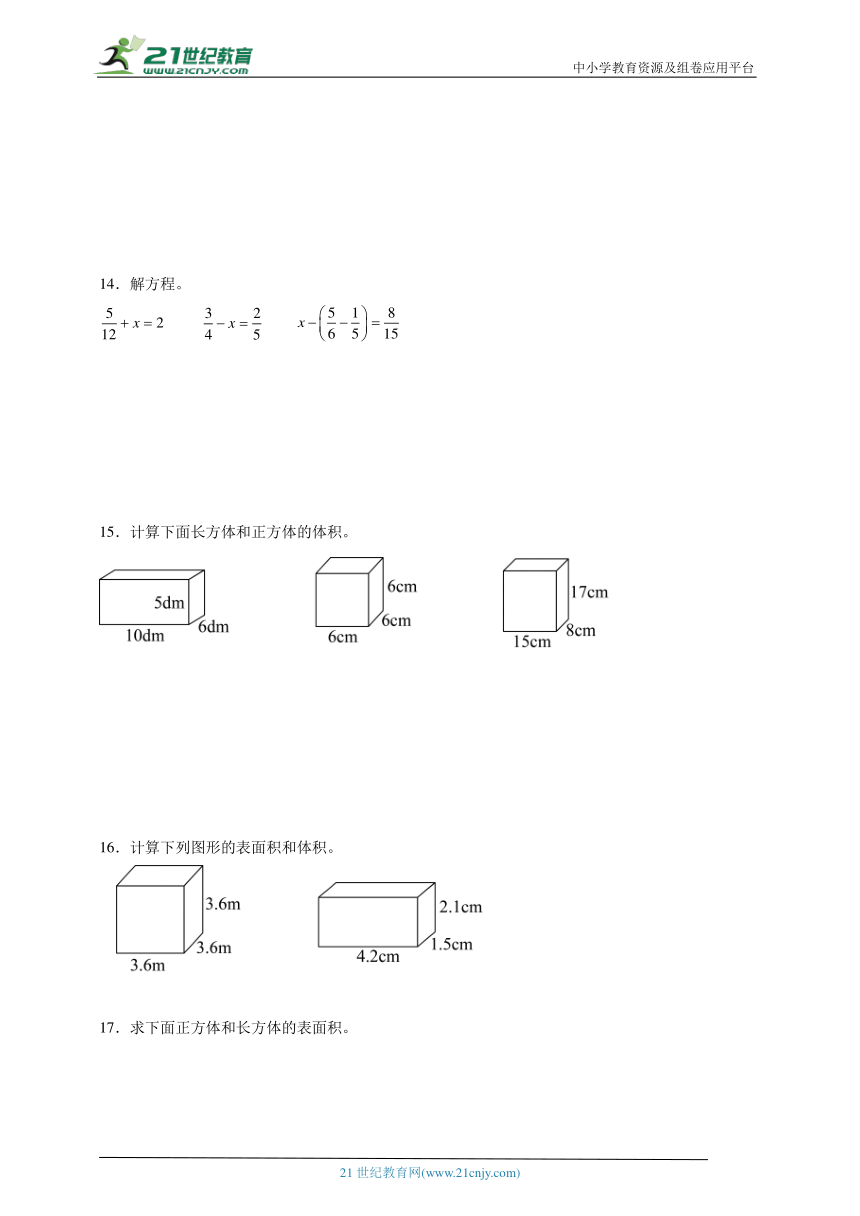
2.脱式计算,能简算的要简算。
0.9+0.99+0.999
3.加减混合计算。(能简算的要简算)
4.用递等式计算,能用简便方法的用简便方法。
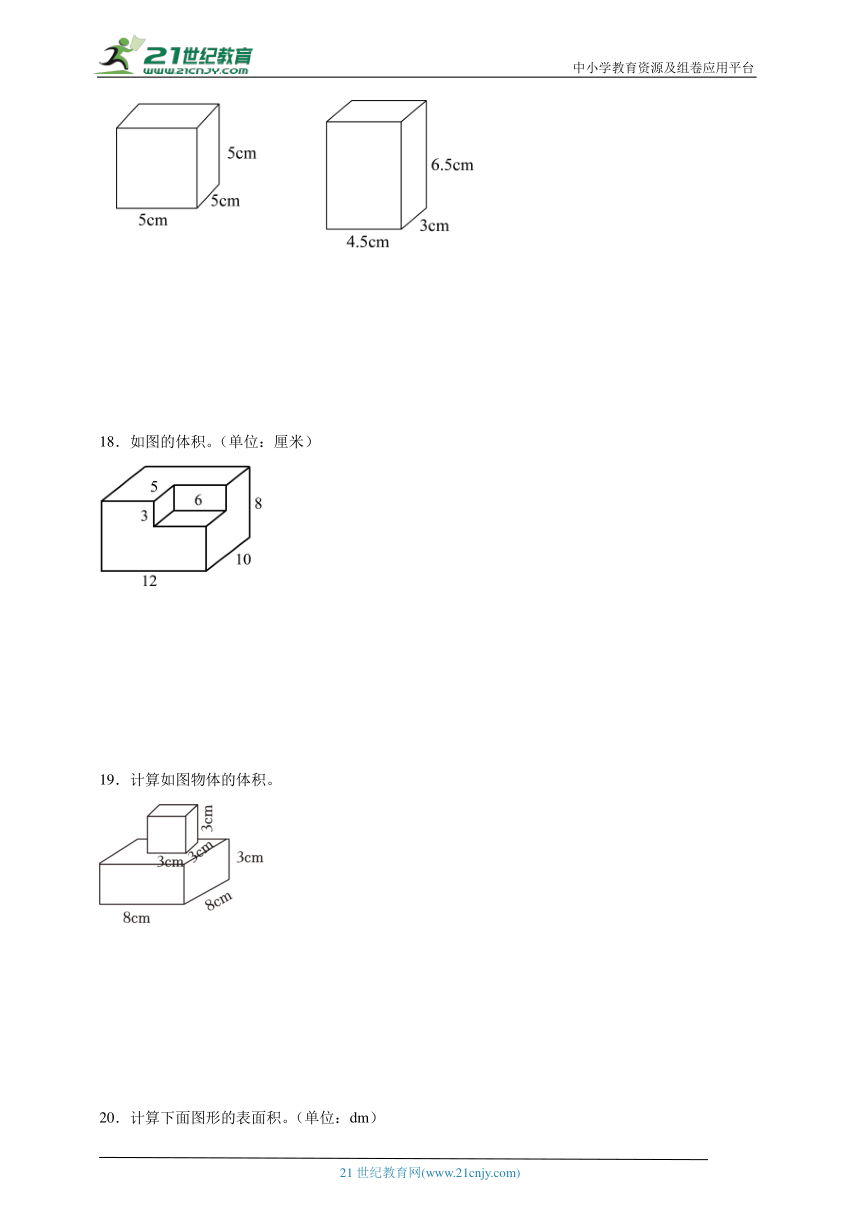
5.计算下面各题,能简算的要简算。
+(+) ++
6-(-) +-+
6.脱式计算,能用简便方法计算的用简便方法计算。
-+ 2-(+) 6.12++2.88+
+-+ ++0.1 -(+)-
7.解方程。
8.解方程。
9.解方程。
10.解方程。
11.解方程。
12.解方程
13.解方程。
= = ()=
14.解方程。
15.计算下面长方体和正方体的体积。
16.计算下列图形的表面积和体积。
17.求下面正方体和长方体的表面积。
18.如图的体积。(单位:厘米)
19.计算如图物体的体积。
20.计算下面图形的表面积。(单位:dm)
21.计算如图图形的表面积和体积。
22.下图为一个长方体展开图,计算这个长方体的体积。(单位:cm)
《期末计算题专项训练-2024-2025学年数学五年级下册人教版》参考答案
1.;1
;2
【分析】(1)去括号,运用减法的性质,式子变为--;
(2)用到减法的性质,把后两个数相加再减,3-(+);
(3)先通分再从左至右依次计算,+-;
(4)用到加法交换律和结合律,先算同分母的加法,式子变为(+)+(+)。
【详解】(1)
=--
=-
=
(2)
=2-(+)
=2-1
=1
(3)
=+-
=-
=
(4)
=(+)+(+)
=1+1
=2
2.2;
;2.889
【分析】(1)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(2)根据减法的性质a-b-c=a-(b+c)进行简算;
(3)先算括号里面的减法,再算括号外面的加法;
(4)把0.9改写成1-0.1,0.99改写成1-0.01,0.999改写成1-0.001,然后根据加法交换律a+b=b+a,减法的性质a-b-c=a-(b+c)进行简算。
【详解】(1)
=
=
=
(2)
=
=
=
(3)
=
=
=
(4)0.9+0.99+0.999
=1-0.1+1-0.01+1-0.001
=1+1+1-0.1-0.01-0.001
=(1+1+1)-(0.1+0.01+0.001)
=3-0.111
=2.889
3.3;;
【分析】,利用加法交换结合律进行简算;
,去括号,括号里的减号变加号,再从左往右算;
,将小数化成分数,从左往右算。
【详解】
4.;
;
【分析】第一个式子利用加法结合律和交换律将同分母的相加可得,再根据解答即可;
第二式子将通分可得,再利用异分母分数的减法法则可得,最后利用分数的减法法则解答即可;
第三个式子去括号得,再通分可得,最后利用异分母分数的减法法则解答即可;
第四个式子先利用异分母分数的加法法则可得,再利用异分母分数的减法法则解答即可。
【详解】
5.;
;1
【分析】+(+),先算小括号里的加法,再算括号外的加法,异分母分数相加减,先通分再计算;
++,利用加法交换律进行简算;
6-(-),先算小括号里的减法,再算括号外的减法;
+-+,交换中间加数和减数的位置,将分母相同的分数结合到一块再计算。
【详解】+(+)
=+(+)
=+
=
=
++
=++
=1+
=
6-(-)
=6-(-)
=6-
=
+-+
=(-)+(+)
=0+1
=1
6.;;10
;;2
【分析】(1)通分后,先算减法,再算加法;
(2)先算括号里面的加法,再算括号外面的减法;
(3)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(4)先交换“+”和“-”的位置,再根据加法结合律(a+b)+c=a+(b+c)进行简算;
(5)先把0.1化成,根据加法交换律a+b=b+a进行简算;
(6)先根据减法的性质逆运算a-(b+c)=a-b-c去掉括号,再根据减法的性质a-b-c=a-(b+c)进行简算。
【详解】(1)-+
=-+
=+
=
(2)2-(+)
=2-(+)
=2-
=
(3)6.12++2.88+
=(6.12+2.88)+(+)
=9+1
=10
(4)+-+
=-++
=(-)+(+)
=+2
=
(5)++0.1
=++
=++
=1+
=
(6)-(+)-
=---
=(-)-(+)
=3-1
=2
7.x=2;;
【分析】“”将等式两边同时减去,解出;
“”将等式两边同时减去,解出;
“”将等式两边同时加上,解出。
【详解】
解:
解:
解:
8.;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上x,然后交换左右两边的位置,再根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上即可。
【详解】
解:
解:
解:
9.;;;
【分析】等式的基本性质1:等式的两边同时加或者减去一个相同的数,等式仍然成立。
异分母分数相加减通分转化为同分母分数相加减。
根据等式的性质1,将等式的两边同时加上;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时加上。
【详解】
解:
解:
解:
解:
10.;;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边同时加上,求出方程的解;
(3)先把方程化简成,然后方程两边先同时加上,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
11.;;
【分析】根据等式性质1,方程两边同时减去,即可求解。
根据等式性质1,方程两边同时加上,即可求解。
根据等式性质1,方程两边同时加上,再同时减去,即可求解。
【详解】
解:
解:
解:
12.;;
【分析】,根据等式的性质1,两边同时-即可;
,根据等式的性质1,两边同时+即可;
,根据等式的性质1,两边同时+,再同时-即可。
【详解】
解:
解:
解:
13.;;
【分析】(1)根据等式的基本性质,方程两边同时减去求解;
(2)根据等式的基本性质,方程两边同时减去求解;
(3)先化简(),再根据等式的基本性质,方程两边同时加上()求解。
【详解】(1)
解:
(2)
解:
(3)
解:
14.;;
【分析】根据等式的性质1,方程的两边同时减去,即可求解;
根据等式的性质1,方程的两边同时加上,再同时减去,即可求解;
先化简为,再根据等式的性质1,方程的两边同时加上,即可求解。
【详解】
解:
解:
解:
15.300;216;2040
【分析】根据长方体的体积=长×宽×高和正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】(1)10×6×5
=60×5
=300()
此长方体的体积是300。
(2)6×6×6
=36×6
=216()
此正方体的体积是216。
(3)15×8×17
=120×17
=2040()
此长方体的体积是2040。
16.正方体的表面积是77.76m2,体积是46.656m3;
长方体的表面积是36.54cm2,体积是13.23cm3
【分析】根据正方体的表面积=棱长×棱长×6、正方体的体积=棱长×棱长×棱长、长方体的表面积=(长×宽+长×高+宽×高)×2、长方体的体积=长×宽×高,代入数据即可解答。
【详解】表面积:3.6×3.6×6
=12.96×6
=77.76(m2)
体积:3.6×3.6×3.6
=12.96×3.6
=46.656(m3)
正方体的表面积是77.76m2,体积是46.656m3。
表面积:(4.2×1.5+4.2×2.1+1.5×2.1)×2
=(6.3+8.82+3.15)×2
=18.27×2
=36.54(cm2)
体积:4.2×1.5×2.1
=6.3×2.1
=13.23(cm3)
长方体的表面积是36.54cm2,体积是13.23cm3。
17.150cm2;124.5cm2
【分析】根据正方体的表面积和长方体的表面积公式,代入数据计算即可。
【详解】正方体表面积:
5×5×6=150(cm2)
(4.5×3+4.5×6.5+3×6.5)×2
=(13.5+29.25+19.5)×2
=62.25×2
=124.5(cm2)
正方体的体积是150cm2,长方体的表面积是124.5cm2
18.870立方厘米
【分析】由图意可知,该立体图形的体积等于长是12厘米,宽是10厘米,高是8厘米的大长方体体积减去长是6厘米,宽是5厘米,高是3厘米的小长方体体积,根据,代入数据计算即可。
【详解】
(立方厘米)
这个图形的体积是870立方厘米。
19.
219cm3
【分析】由图可知,物体的体积是正方体体积与长方体体积的和,根据和计算即可。
【详解】
(cm3)
20.1020dm2
【分析】图形的表面积等于长是20dm、宽是6dm、高是15dm的长方体的表面积加上长是6dm、宽是20-7×2=6(dm)的两个正方形的面积,再减去边长为6dm的两个正方形的面积;所以图形的表面积就是长是20dm、宽是6dm、高是15dm的长方体的表面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】20-7×2
=20-14
=6(dm)
(20×6+20×15+15×6)×2
=(120+300+90)×2
=(420+90)×2
=510×2
=1020(dm2)
21.328平方分米;336立方分米
【分析】根据正方体的表面积=棱长×棱长×6,长方体的表面积=(长×宽+长×高+宽×高)×2,先算出正方体和长方体的表面积再加起来,再减去长方体和正方体相连那里的两个正方形的面积,算出来就是这个图形的表面积。
根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,算出正方体和长方体的体积再相加,就可以求出这个图形的体积。据此解答。
【详解】表面积:
6×6×6=216(平方分米)
(2×6+2×10+6×10)×2
=(12+20+60)×2
=92×2
=184(平方分米)
6×6×2=72(平方分米)
216+184-72=328(平方分米)
体积:
6×6×6+2×6×10
=216+120
=336(立方分米)
22.120cm3
【分析】观察长方体展开图可知,长方体的高4cm,宽是(9-4)cm,长是(20÷2-4)cm,根据长方体体积=长×宽×高,列式计算即可。
【详解】9-4=5(cm)
20÷2-4
=10-4
=6(cm)
6×5×4=120(cm3)
这个长方体的体积是120cm3。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末计算题专项训练-2024-2025学年数学五年级下册人教版
1.能简便的要简便运算。
2.脱式计算,能简算的要简算。
0.9+0.99+0.999
3.加减混合计算。(能简算的要简算)
4.用递等式计算,能用简便方法的用简便方法。
5.计算下面各题,能简算的要简算。
+(+) ++
6-(-) +-+
6.脱式计算,能用简便方法计算的用简便方法计算。
-+ 2-(+) 6.12++2.88+
+-+ ++0.1 -(+)-
7.解方程。
8.解方程。
9.解方程。
10.解方程。
11.解方程。
12.解方程
13.解方程。
= = ()=
14.解方程。
15.计算下面长方体和正方体的体积。
16.计算下列图形的表面积和体积。
17.求下面正方体和长方体的表面积。
18.如图的体积。(单位:厘米)
19.计算如图物体的体积。
20.计算下面图形的表面积。(单位:dm)
21.计算如图图形的表面积和体积。
22.下图为一个长方体展开图,计算这个长方体的体积。(单位:cm)
《期末计算题专项训练-2024-2025学年数学五年级下册人教版》参考答案
1.;1
;2
【分析】(1)去括号,运用减法的性质,式子变为--;
(2)用到减法的性质,把后两个数相加再减,3-(+);
(3)先通分再从左至右依次计算,+-;
(4)用到加法交换律和结合律,先算同分母的加法,式子变为(+)+(+)。
【详解】(1)
=--
=-
=
(2)
=2-(+)
=2-1
=1
(3)
=+-
=-
=
(4)
=(+)+(+)
=1+1
=2
2.2;
;2.889
【分析】(1)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(2)根据减法的性质a-b-c=a-(b+c)进行简算;
(3)先算括号里面的减法,再算括号外面的加法;
(4)把0.9改写成1-0.1,0.99改写成1-0.01,0.999改写成1-0.001,然后根据加法交换律a+b=b+a,减法的性质a-b-c=a-(b+c)进行简算。
【详解】(1)
=
=
=
(2)
=
=
=
(3)
=
=
=
(4)0.9+0.99+0.999
=1-0.1+1-0.01+1-0.001
=1+1+1-0.1-0.01-0.001
=(1+1+1)-(0.1+0.01+0.001)
=3-0.111
=2.889
3.3;;
【分析】,利用加法交换结合律进行简算;
,去括号,括号里的减号变加号,再从左往右算;
,将小数化成分数,从左往右算。
【详解】
4.;
;
【分析】第一个式子利用加法结合律和交换律将同分母的相加可得,再根据解答即可;
第二式子将通分可得,再利用异分母分数的减法法则可得,最后利用分数的减法法则解答即可;
第三个式子去括号得,再通分可得,最后利用异分母分数的减法法则解答即可;
第四个式子先利用异分母分数的加法法则可得,再利用异分母分数的减法法则解答即可。
【详解】
5.;
;1
【分析】+(+),先算小括号里的加法,再算括号外的加法,异分母分数相加减,先通分再计算;
++,利用加法交换律进行简算;
6-(-),先算小括号里的减法,再算括号外的减法;
+-+,交换中间加数和减数的位置,将分母相同的分数结合到一块再计算。
【详解】+(+)
=+(+)
=+
=
=
++
=++
=1+
=
6-(-)
=6-(-)
=6-
=
+-+
=(-)+(+)
=0+1
=1
6.;;10
;;2
【分析】(1)通分后,先算减法,再算加法;
(2)先算括号里面的加法,再算括号外面的减法;
(3)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(4)先交换“+”和“-”的位置,再根据加法结合律(a+b)+c=a+(b+c)进行简算;
(5)先把0.1化成,根据加法交换律a+b=b+a进行简算;
(6)先根据减法的性质逆运算a-(b+c)=a-b-c去掉括号,再根据减法的性质a-b-c=a-(b+c)进行简算。
【详解】(1)-+
=-+
=+
=
(2)2-(+)
=2-(+)
=2-
=
(3)6.12++2.88+
=(6.12+2.88)+(+)
=9+1
=10
(4)+-+
=-++
=(-)+(+)
=+2
=
(5)++0.1
=++
=++
=1+
=
(6)-(+)-
=---
=(-)-(+)
=3-1
=2
7.x=2;;
【分析】“”将等式两边同时减去,解出;
“”将等式两边同时减去,解出;
“”将等式两边同时加上,解出。
【详解】
解:
解:
解:
8.;;
【分析】,根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上x,然后交换左右两边的位置,再根据等式的性质1,将方程左右两边同时减去即可;
,根据等式的性质1,将方程左右两边同时加上即可。
【详解】
解:
解:
解:
9.;;;
【分析】等式的基本性质1:等式的两边同时加或者减去一个相同的数,等式仍然成立。
异分母分数相加减通分转化为同分母分数相加减。
根据等式的性质1,将等式的两边同时加上;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时减;
根据等式的性质1,将等式的两边同时加上。
【详解】
解:
解:
解:
解:
10.;;
【分析】根据等式的性质解方程。
(1)方程两边同时减去,求出方程的解;
(2)方程两边同时加上,求出方程的解;
(3)先把方程化简成,然后方程两边先同时加上,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
11.;;
【分析】根据等式性质1,方程两边同时减去,即可求解。
根据等式性质1,方程两边同时加上,即可求解。
根据等式性质1,方程两边同时加上,再同时减去,即可求解。
【详解】
解:
解:
解:
12.;;
【分析】,根据等式的性质1,两边同时-即可;
,根据等式的性质1,两边同时+即可;
,根据等式的性质1,两边同时+,再同时-即可。
【详解】
解:
解:
解:
13.;;
【分析】(1)根据等式的基本性质,方程两边同时减去求解;
(2)根据等式的基本性质,方程两边同时减去求解;
(3)先化简(),再根据等式的基本性质,方程两边同时加上()求解。
【详解】(1)
解:
(2)
解:
(3)
解:
14.;;
【分析】根据等式的性质1,方程的两边同时减去,即可求解;
根据等式的性质1,方程的两边同时加上,再同时减去,即可求解;
先化简为,再根据等式的性质1,方程的两边同时加上,即可求解。
【详解】
解:
解:
解:
15.300;216;2040
【分析】根据长方体的体积=长×宽×高和正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】(1)10×6×5
=60×5
=300()
此长方体的体积是300。
(2)6×6×6
=36×6
=216()
此正方体的体积是216。
(3)15×8×17
=120×17
=2040()
此长方体的体积是2040。
16.正方体的表面积是77.76m2,体积是46.656m3;
长方体的表面积是36.54cm2,体积是13.23cm3
【分析】根据正方体的表面积=棱长×棱长×6、正方体的体积=棱长×棱长×棱长、长方体的表面积=(长×宽+长×高+宽×高)×2、长方体的体积=长×宽×高,代入数据即可解答。
【详解】表面积:3.6×3.6×6
=12.96×6
=77.76(m2)
体积:3.6×3.6×3.6
=12.96×3.6
=46.656(m3)
正方体的表面积是77.76m2,体积是46.656m3。
表面积:(4.2×1.5+4.2×2.1+1.5×2.1)×2
=(6.3+8.82+3.15)×2
=18.27×2
=36.54(cm2)
体积:4.2×1.5×2.1
=6.3×2.1
=13.23(cm3)
长方体的表面积是36.54cm2,体积是13.23cm3。
17.150cm2;124.5cm2
【分析】根据正方体的表面积和长方体的表面积公式,代入数据计算即可。
【详解】正方体表面积:
5×5×6=150(cm2)
(4.5×3+4.5×6.5+3×6.5)×2
=(13.5+29.25+19.5)×2
=62.25×2
=124.5(cm2)
正方体的体积是150cm2,长方体的表面积是124.5cm2
18.870立方厘米
【分析】由图意可知,该立体图形的体积等于长是12厘米,宽是10厘米,高是8厘米的大长方体体积减去长是6厘米,宽是5厘米,高是3厘米的小长方体体积,根据,代入数据计算即可。
【详解】
(立方厘米)
这个图形的体积是870立方厘米。
19.
219cm3
【分析】由图可知,物体的体积是正方体体积与长方体体积的和,根据和计算即可。
【详解】
(cm3)
20.1020dm2
【分析】图形的表面积等于长是20dm、宽是6dm、高是15dm的长方体的表面积加上长是6dm、宽是20-7×2=6(dm)的两个正方形的面积,再减去边长为6dm的两个正方形的面积;所以图形的表面积就是长是20dm、宽是6dm、高是15dm的长方体的表面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】20-7×2
=20-14
=6(dm)
(20×6+20×15+15×6)×2
=(120+300+90)×2
=(420+90)×2
=510×2
=1020(dm2)
21.328平方分米;336立方分米
【分析】根据正方体的表面积=棱长×棱长×6,长方体的表面积=(长×宽+长×高+宽×高)×2,先算出正方体和长方体的表面积再加起来,再减去长方体和正方体相连那里的两个正方形的面积,算出来就是这个图形的表面积。
根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,算出正方体和长方体的体积再相加,就可以求出这个图形的体积。据此解答。
【详解】表面积:
6×6×6=216(平方分米)
(2×6+2×10+6×10)×2
=(12+20+60)×2
=92×2
=184(平方分米)
6×6×2=72(平方分米)
216+184-72=328(平方分米)
体积:
6×6×6+2×6×10
=216+120
=336(立方分米)
22.120cm3
【分析】观察长方体展开图可知,长方体的高4cm,宽是(9-4)cm,长是(20÷2-4)cm,根据长方体体积=长×宽×高,列式计算即可。
【详解】9-4=5(cm)
20÷2-4
=10-4
=6(cm)
6×5×4=120(cm3)
这个长方体的体积是120cm3。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
