期末计算题专项训练(含解析)-2024-2025学年数学五年级下册苏教版
文档属性
| 名称 | 期末计算题专项训练(含解析)-2024-2025学年数学五年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 956.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 19:32:51 | ||
图片预览


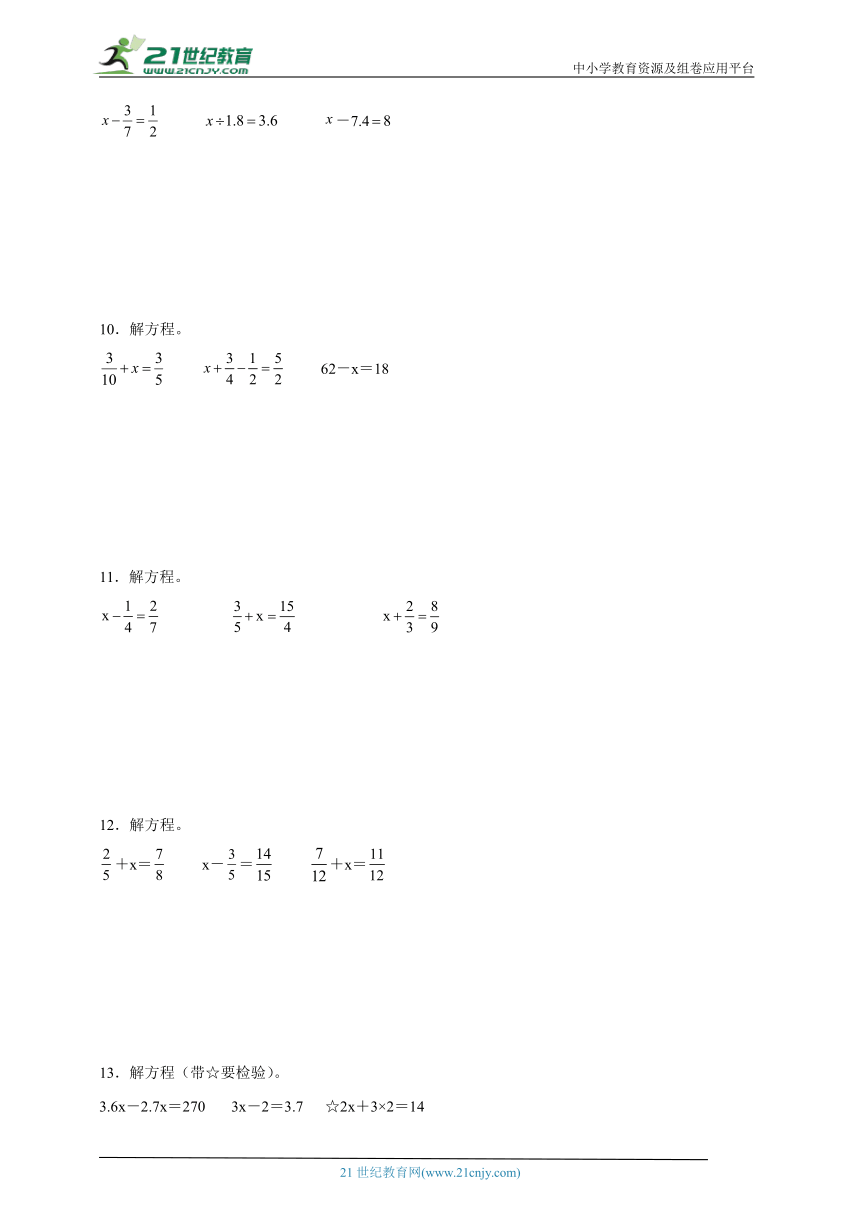


文档简介
中小学教育资源及组卷应用平台
期末计算题专项训练-2024-2025学年数学五年级下册苏教版
1.计算下面各题。
2.下面各题,怎样算简便就怎样算。
3.计算下面各题,能简算的要简算。
4.计算下面各题,能简算的要简算。
5.计算下面各题,能简算的要简算。
6.计算下面各题。
7.怎样算简便就怎样算。
8.计算下面各题。
9.解方程。
-7.4
10.解方程。
62-x=18
11.解方程。
12.解方程。
+x= x-= +x=
13.解方程(带☆要检验)。
3.6x-2.7x=270 3x-2=3.7 ☆2x+3×2=14
14.解方程。
3(x+4.8)=16.5 3.5x-6×2.8=4.2
15.解方程。
0.9+0.3=2.4 1.8-2.7=15.3
16.解方程。
17.求涂色部分的周长。
18.求下面大正方形中涂色部分的面积。(单位:厘米)
19.求涂色部分的面积。(单位:厘米)
20.求涂色部分的面积。
21.求涂色部分的面积。
22.求涂色部分的面积。
23.求涂色部分的面积。
24.求涂色部分的面积。(单位:厘米)
《期末计算题专项训练-2024-2025学年数学五年级下册苏教版》参考答案
1.;;
【分析】(1)先通分为分母是12的分数,再根据四则运算的顺序,先算加法,再算减法;
(2)先通分为分母是72的分数,再根据四则运算的顺序,先算减法,再算加法;
(3)根据四则运算的顺序,先算括号里的减法,把括号里的分母化成是9的分数,最后算括号外的减法,把分母化成是18的分数再进行计算。
【详解】(1)
=
=
=
=
(2)
=
=
=
(3)
=
=
=
=
2.;;
【分析】(1)从左往右依次计算;
(2)先算括号里面的加法,再算括号外面的减法;
(3)先交换“”和“”的位置,然后根据减法的性质a-b+c=a-(b-c)把变成,再按顺序计算。
【详解】(1)
(2)
(3)
3.1;0;(或)
【分析】先观察分数分母,4、6、12的最小公倍数是12,将所有分数通分为分母是12的分数,然后按照从左到右的顺序进行同分母分数的加减运算;
观察式子发现,后面两个分数分母相同,一个数连续减去两个数,等于这个数减去这两个数的和,可先将后面两个分数相加,再用1减去它们的和,这样计算更简便;
观察到式子中和分母相同,根据加法交换律,交换和的位置,先计算+,得到整数1后,再加上,可简化计算过程。
【详解】
=
=
=
=
=
=
=
=
=
=(或)
4.;4;
【分析】(1)先通分,把分数化成同分母分数,再按照从左往右的顺序计算即可;
(2)根据减法的性质a-b-c=a-(b+c)把算式写成5-(+),再进一步计算即可;
(3)先把算式写成+-+,再利用带符号搬家和加法结合律把算式写成-+(+),再进一步计算即可。
【详解】-+
=-+
=+
=
5--
=5-(+)
=5-1
=4
+(-)+
=+-+
=-+(+)
=-+(+)
=+1
=
5.;;
【分析】(1)先逆用减法的性质去括号,再同分母分数结合简算。
(2)先带着运算符号交换减数和加数的位置,交换和的位置,同分母分数进行计算,再根据加法结合律、减法的性质,变原式为:进行简便计算即可。
(3)根据减法的性质,变原式为:进行简便计算即可。
【详解】
6.;;;
【分析】-(-),先计算括号里的减法,再计算括号外的减法;
4-(-),先计算括号里的减法,再计算括号外的减法;
+(-),先计算括号里的减法,再计算括号外的加法;
1--,按照运算顺序,从左向右进行计算。
【详解】-(-)
=-(-)
=-
=-
=
4-(-)
=4-(-)
=4-
=
+(-)
=+(-)
=+
=+
=
1--
=-
=-
=
7.;5;;
【分析】(1)运用加法交换律和加法结合律,把原式化为,依此进行计算即可;
(2)运用减法的性质,把原式化为,依此进行计算即可;
(3)运用加法交换律,把原式化为,然后先算括号里面的,再算括号外面即可;
(4)运用带符号搬家和减法的性质,把原式化为,依此进行计算即可。
【详解】
=
=
=
=
=
=
=5
=
=
=
=
=
=
=
8.;;;
【分析】(1)(2)(3)按照从左到右的运算顺序进行计算即可;
(4)运用带符号搬家,把原式化为,依此进行计算即可。
【详解】
=
=
=
=
=
=
=
=
=
9.;;
【分析】(1)根据等式的基本性质1,等式两边同时加,计算即可得解。
(2)根据等式的基本性质2,等式两边同时乘1.8,计算即可得解。
(3)根据等式的基本性质1,等式两边同时加7.4,计算即可得解。
【详解】(1)
解:
(2)
解:
(3)
解:
10.x=;x=;x=44
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
(1)根据等式的性质1,方程两边同时减去,解出方程;
(2)根据等式的性质1,方程两边同时加上再同时减去,解出方程;
(3)根据等式的性质1和减法的性质,方程转化为x=62-18,解出方程。
【详解】
解:
解:
62-x=18
解:x=62-18
x=44
11.x=;x=;x=
【分析】(1)根据等式的基本性质1给方程两边同时加上即可;
(2)根据等式的基本性质1给方程两边同时减去即可;
(3)根据等式的基本性质1给方程两边同时减去即可。
【详解】x-=
解:x-+=+
x=+
x=
+x=
解:+x-=-
x=-
x=
x+=
解:x+-=-
x=-
x=
12.x=;x=;x=
【分析】+x=,根据等式的性质1,方程两边同时减去即可。
x-=,根据等式的性质1,方程两边同时加上即可。
+x=,根据等式的性质1,方程两边同时减去即可。
【详解】+x=
解:+x-=-
x=-
x=
x-=
解:x-+=+
x=+
x=
+x=
解:+x-=-
x=
13.x=300;x=1.9;x=4
【分析】根据等式的性质求出方程的解。
(1)先把方程化简成0.9x=270,然后方程两边同时除以0.9,求出方程的解;
(2)方程两边先同时加上2,再同时除以3,求出方程的解;
(3)先把方程化简成2x+6=14,然后方程两边先同时减去6,再同时除以2,求出方程的解。
【详解】(1)3.6x-2.7x=270
解:0.9x=270
0.9x÷0.9=270÷0.9
x=300
(2)3x-2=3.7
解:3x-2+2=3.7+2
3x=5.7
3x÷3=5.7÷3
x=1.9
(3)2x+3×2=14
解:2x+6=14
2x+6-6=14-6
2x=8
2x÷2=8÷2
x=4
检验:方程左边=2x+3×2
=2×4+3×2
=8+6
=14
=方程右边
所以,x=4是方程的解。
14.;x=0.7;x=6
【分析】(1)利用等式的性质1,方程两边同时加上即可求解;
(2)利用等式的性质2,方程两边同时除以3,再利用等式的性质1,方程两边同时减去4.8即可求解;
(3)先计算6×2.8=16.8,再利用等式的性质1,方程两边同时加上16.8,最后利用等式的性质2,方程两边同时除以3.5即可求解。
【详解】
解:
3(x+4.8)=16.5
解:3(x+4.8)÷3=16.5÷3
x+4.8=16.5÷3
x+4.8=5.5
x+4.8-4.8=5.5-4.8
x=0.7
3.5x-6×2.8=4.2
解:3.5x-16.8=4.2
3.5x-16.8+16.8=4.2+16.8
3.5x=21
3.5x÷3.5=21÷3.5
x=6
15.;=2;=10
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)先把方程化简成1.2=2.4,然后方程两边同时除以1.2,求出方程的解;
(3)方程两边先同时加上2.7,再同时除以1.8,求出方程的解。
【详解】(1)
解:
(2)0.9+0.3=2.4
解:1.2=2.4
1.2÷1.2=2.4÷1.2
=2
(3)1.8-2.7=15.3
解:1.8-2.7+2.7=15.3+2.7
1.8=18
1.8÷1.8=18÷1.8
=10
16.;;;
;;
【分析】(1)方程的两边同时减去37即可得到未知数的值。
(2)先计算方程的左边,方程的两边同时除以62即可得到未知数的值。
(3)先计算方程的左边,方程的两边同时除以1.8即可得到未知数的值。
(4)方程的两边同时乘12即可得到未知数的值。
(5)方程的两边同时加上6.2,再同时除以0.9即可得到未知数的值。
(6)先计算方程的左边为,然后方程的两边同时加上4,再同时除以2.5即可得到未知数的值。
【详解】
解:
解:
解:
解:
解:
解:
17.102.8米;35.7厘米
【分析】第一个图形:周长=直径是20米的圆的周长+两条直径的长;根据圆的周长公式:周长=π×直径,据此求出阴影部分的周长。
第二个图形:周长=长是10厘米,宽是(10÷2)厘米的长方形长+两条宽+直径是10厘米圆的周长的一半,据此求出阴影部分的周长。
【详解】第一个图形:
3.14×20+20×2
=62.8+40
=102.8(米)
阴影部分周长是102.8米。
第二个图形:
10+(10÷2)×2+3.14×10÷2
=10+5×2+31.4÷2
=10+10+15.7
=20+15.7
=35.7(厘米)
阴影部分周长是35.7厘米。
18.30.96平方厘米;72平方厘米
【分析】(1)观察图形,4个完全一样的圆可以组成一个圆,则涂色部分的面积=正方形的面积-圆的面积,根据正方形的面积公式S=a2,圆的面积公式S=πr2,代入数据计算求解。
(2)如下图,把右边的涂色部分移补到左边,这样涂色部分合起来是一个长方形,面积是正方形面积的一半,根据正方形的面积公式S=a2,代入数据计算求解。
【详解】(1)6+6=12(厘米)
12×12-3.14×62
=12×12-3.14×36
=144-113.04
=30.96(平方厘米)
涂色部分的面积是30.96平方厘米。
(2)12×12÷2
=144÷2
=72(平方厘米)
涂色部分的面积是72平方厘米。
19.7.74平方厘米;4平方厘米
【分析】左图:观察图形可知,涂色部分的面积等于正方形的面积减去两个半圆的面积,而两个半圆正好可以组成一个完整的圆,所以用正方形面积减去圆的面积即可;
右图:观察发现,通过割补法,可将左边半圆内的涂色部分移到右边,此时涂色部分组合成一个三角形,三角形的底是右边竖线段的长度4厘米,高是圆的半径4÷2=2(厘米),根据“三角形面积=底×高÷2”算出面积即可。
【详解】左图:6×6=36(平方厘米)
6÷2=3(厘米)
3.14×32=28.26(平方厘米)
36-28.26=7.74(平方厘米)
所以左图涂色部分面积是7.74平方厘米。
右图:4÷2=2(厘米)
4×2÷2=4(平方厘米)
所以右图涂色部分面积是4平方厘米。
【点睛】在解决这类求涂色部分面积的问题时,核心在于把不规则图形转化为规则图形,将复杂问题简单化。左图需要捕捉到两个半圆能拼成一个完整的圆;右图则需要合理割补,将分散的涂色部分重新组合,化零为整,降低计算难度。
20.43.74dm2;25.12dm2
【分析】(1)观察图形,两个完全一样的半圆可以组成一个圆;则涂色部分的面积=长方形的面积-圆的面积,根据长方形的面积公式S=ab,圆的面积公式S=πr2,代入数据计算求解。
(2)观察图形可知,涂色部分的面积=大圆的面积-2个小圆的面积,根据圆的面积公式S=πr2,代入数据计算求解。
【详解】(1)12×6-3.14×(6÷2)2
=12×6-3.14×32
=12×6-3.14×9
=72-28.26
=43.74(dm2)
涂色部分的面积是43.74dm2。
(2)大圆半径:8÷2=4(dm)
小圆半径:8÷4=2(dm)
3.14×42-3.14×22×2
=3.14×16-3.14×4×2
=50.24-25.12
=25.12(dm2)
涂色部分的面积是25.12dm2。
21.12.56
【分析】由图可知,通过旋转涂色半圆可将涂色部分变成半径是4 的圆的,要求涂色部分的面积,可求出半径是4 的圆的面积,再除以4即可。
【详解】3.14×42÷4
=3.14×16÷4
=50.24÷4
=12.56
22.15.25
【分析】涂色部分的面积等于直径为10的半圆的面积减去底为8、高为6的直角三角形的面积,根据圆的面积=圆周率×半径的平方,求出圆的面积,再除以2求出半圆的面积,根据三角形的面积=底×高÷2求出三角形的面积,再用半圆的面积减去三角形的面积即可解答。
【详解】10÷2=5
3.14×52÷2-6×8÷2
=3.14×25÷2-48÷2
=78.5÷2-24
=39.25-24
=15.25
23.5.375
【分析】根据题意可知,每个扇形的半径相当于正方形边长的一半,也就是(5÷2),空白部分的面积可以组合成一个圆的面积,所以阴影部分的面积等于正方形的面积减去圆的面积;根据正方形的面积=边长×边长、圆的面积公式:S=πr2,代入数据分别求出正方形的面积、圆的面积,进而求出阴影部分的面积。
【详解】5÷2=2.5
5×5-3.14×2.52
=5×5-3.14×6.25
=25-19.625
=5.375
阴影部分的面积是5.375。
24.28.26平方厘米
【分析】通过旋转,涂色部分可以拼成圆,涂色部分的面积=圆周率×半径的平方×,据此列式计算。
【详解】3.14×62×
=3.14×36×
=3.14×(36×)
=3.14×9
=28.26(平方厘米)
涂色部分的面积是28.26平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末计算题专项训练-2024-2025学年数学五年级下册苏教版
1.计算下面各题。
2.下面各题,怎样算简便就怎样算。
3.计算下面各题,能简算的要简算。
4.计算下面各题,能简算的要简算。
5.计算下面各题,能简算的要简算。
6.计算下面各题。
7.怎样算简便就怎样算。
8.计算下面各题。
9.解方程。
-7.4
10.解方程。
62-x=18
11.解方程。
12.解方程。
+x= x-= +x=
13.解方程(带☆要检验)。
3.6x-2.7x=270 3x-2=3.7 ☆2x+3×2=14
14.解方程。
3(x+4.8)=16.5 3.5x-6×2.8=4.2
15.解方程。
0.9+0.3=2.4 1.8-2.7=15.3
16.解方程。
17.求涂色部分的周长。
18.求下面大正方形中涂色部分的面积。(单位:厘米)
19.求涂色部分的面积。(单位:厘米)
20.求涂色部分的面积。
21.求涂色部分的面积。
22.求涂色部分的面积。
23.求涂色部分的面积。
24.求涂色部分的面积。(单位:厘米)
《期末计算题专项训练-2024-2025学年数学五年级下册苏教版》参考答案
1.;;
【分析】(1)先通分为分母是12的分数,再根据四则运算的顺序,先算加法,再算减法;
(2)先通分为分母是72的分数,再根据四则运算的顺序,先算减法,再算加法;
(3)根据四则运算的顺序,先算括号里的减法,把括号里的分母化成是9的分数,最后算括号外的减法,把分母化成是18的分数再进行计算。
【详解】(1)
=
=
=
=
(2)
=
=
=
(3)
=
=
=
=
2.;;
【分析】(1)从左往右依次计算;
(2)先算括号里面的加法,再算括号外面的减法;
(3)先交换“”和“”的位置,然后根据减法的性质a-b+c=a-(b-c)把变成,再按顺序计算。
【详解】(1)
(2)
(3)
3.1;0;(或)
【分析】先观察分数分母,4、6、12的最小公倍数是12,将所有分数通分为分母是12的分数,然后按照从左到右的顺序进行同分母分数的加减运算;
观察式子发现,后面两个分数分母相同,一个数连续减去两个数,等于这个数减去这两个数的和,可先将后面两个分数相加,再用1减去它们的和,这样计算更简便;
观察到式子中和分母相同,根据加法交换律,交换和的位置,先计算+,得到整数1后,再加上,可简化计算过程。
【详解】
=
=
=
=
=
=
=
=
=
=(或)
4.;4;
【分析】(1)先通分,把分数化成同分母分数,再按照从左往右的顺序计算即可;
(2)根据减法的性质a-b-c=a-(b+c)把算式写成5-(+),再进一步计算即可;
(3)先把算式写成+-+,再利用带符号搬家和加法结合律把算式写成-+(+),再进一步计算即可。
【详解】-+
=-+
=+
=
5--
=5-(+)
=5-1
=4
+(-)+
=+-+
=-+(+)
=-+(+)
=+1
=
5.;;
【分析】(1)先逆用减法的性质去括号,再同分母分数结合简算。
(2)先带着运算符号交换减数和加数的位置,交换和的位置,同分母分数进行计算,再根据加法结合律、减法的性质,变原式为:进行简便计算即可。
(3)根据减法的性质,变原式为:进行简便计算即可。
【详解】
6.;;;
【分析】-(-),先计算括号里的减法,再计算括号外的减法;
4-(-),先计算括号里的减法,再计算括号外的减法;
+(-),先计算括号里的减法,再计算括号外的加法;
1--,按照运算顺序,从左向右进行计算。
【详解】-(-)
=-(-)
=-
=-
=
4-(-)
=4-(-)
=4-
=
+(-)
=+(-)
=+
=+
=
1--
=-
=-
=
7.;5;;
【分析】(1)运用加法交换律和加法结合律,把原式化为,依此进行计算即可;
(2)运用减法的性质,把原式化为,依此进行计算即可;
(3)运用加法交换律,把原式化为,然后先算括号里面的,再算括号外面即可;
(4)运用带符号搬家和减法的性质,把原式化为,依此进行计算即可。
【详解】
=
=
=
=
=
=
=5
=
=
=
=
=
=
=
8.;;;
【分析】(1)(2)(3)按照从左到右的运算顺序进行计算即可;
(4)运用带符号搬家,把原式化为,依此进行计算即可。
【详解】
=
=
=
=
=
=
=
=
=
9.;;
【分析】(1)根据等式的基本性质1,等式两边同时加,计算即可得解。
(2)根据等式的基本性质2,等式两边同时乘1.8,计算即可得解。
(3)根据等式的基本性质1,等式两边同时加7.4,计算即可得解。
【详解】(1)
解:
(2)
解:
(3)
解:
10.x=;x=;x=44
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
(1)根据等式的性质1,方程两边同时减去,解出方程;
(2)根据等式的性质1,方程两边同时加上再同时减去,解出方程;
(3)根据等式的性质1和减法的性质,方程转化为x=62-18,解出方程。
【详解】
解:
解:
62-x=18
解:x=62-18
x=44
11.x=;x=;x=
【分析】(1)根据等式的基本性质1给方程两边同时加上即可;
(2)根据等式的基本性质1给方程两边同时减去即可;
(3)根据等式的基本性质1给方程两边同时减去即可。
【详解】x-=
解:x-+=+
x=+
x=
+x=
解:+x-=-
x=-
x=
x+=
解:x+-=-
x=-
x=
12.x=;x=;x=
【分析】+x=,根据等式的性质1,方程两边同时减去即可。
x-=,根据等式的性质1,方程两边同时加上即可。
+x=,根据等式的性质1,方程两边同时减去即可。
【详解】+x=
解:+x-=-
x=-
x=
x-=
解:x-+=+
x=+
x=
+x=
解:+x-=-
x=
13.x=300;x=1.9;x=4
【分析】根据等式的性质求出方程的解。
(1)先把方程化简成0.9x=270,然后方程两边同时除以0.9,求出方程的解;
(2)方程两边先同时加上2,再同时除以3,求出方程的解;
(3)先把方程化简成2x+6=14,然后方程两边先同时减去6,再同时除以2,求出方程的解。
【详解】(1)3.6x-2.7x=270
解:0.9x=270
0.9x÷0.9=270÷0.9
x=300
(2)3x-2=3.7
解:3x-2+2=3.7+2
3x=5.7
3x÷3=5.7÷3
x=1.9
(3)2x+3×2=14
解:2x+6=14
2x+6-6=14-6
2x=8
2x÷2=8÷2
x=4
检验:方程左边=2x+3×2
=2×4+3×2
=8+6
=14
=方程右边
所以,x=4是方程的解。
14.;x=0.7;x=6
【分析】(1)利用等式的性质1,方程两边同时加上即可求解;
(2)利用等式的性质2,方程两边同时除以3,再利用等式的性质1,方程两边同时减去4.8即可求解;
(3)先计算6×2.8=16.8,再利用等式的性质1,方程两边同时加上16.8,最后利用等式的性质2,方程两边同时除以3.5即可求解。
【详解】
解:
3(x+4.8)=16.5
解:3(x+4.8)÷3=16.5÷3
x+4.8=16.5÷3
x+4.8=5.5
x+4.8-4.8=5.5-4.8
x=0.7
3.5x-6×2.8=4.2
解:3.5x-16.8=4.2
3.5x-16.8+16.8=4.2+16.8
3.5x=21
3.5x÷3.5=21÷3.5
x=6
15.;=2;=10
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)先把方程化简成1.2=2.4,然后方程两边同时除以1.2,求出方程的解;
(3)方程两边先同时加上2.7,再同时除以1.8,求出方程的解。
【详解】(1)
解:
(2)0.9+0.3=2.4
解:1.2=2.4
1.2÷1.2=2.4÷1.2
=2
(3)1.8-2.7=15.3
解:1.8-2.7+2.7=15.3+2.7
1.8=18
1.8÷1.8=18÷1.8
=10
16.;;;
;;
【分析】(1)方程的两边同时减去37即可得到未知数的值。
(2)先计算方程的左边,方程的两边同时除以62即可得到未知数的值。
(3)先计算方程的左边,方程的两边同时除以1.8即可得到未知数的值。
(4)方程的两边同时乘12即可得到未知数的值。
(5)方程的两边同时加上6.2,再同时除以0.9即可得到未知数的值。
(6)先计算方程的左边为,然后方程的两边同时加上4,再同时除以2.5即可得到未知数的值。
【详解】
解:
解:
解:
解:
解:
解:
17.102.8米;35.7厘米
【分析】第一个图形:周长=直径是20米的圆的周长+两条直径的长;根据圆的周长公式:周长=π×直径,据此求出阴影部分的周长。
第二个图形:周长=长是10厘米,宽是(10÷2)厘米的长方形长+两条宽+直径是10厘米圆的周长的一半,据此求出阴影部分的周长。
【详解】第一个图形:
3.14×20+20×2
=62.8+40
=102.8(米)
阴影部分周长是102.8米。
第二个图形:
10+(10÷2)×2+3.14×10÷2
=10+5×2+31.4÷2
=10+10+15.7
=20+15.7
=35.7(厘米)
阴影部分周长是35.7厘米。
18.30.96平方厘米;72平方厘米
【分析】(1)观察图形,4个完全一样的圆可以组成一个圆,则涂色部分的面积=正方形的面积-圆的面积,根据正方形的面积公式S=a2,圆的面积公式S=πr2,代入数据计算求解。
(2)如下图,把右边的涂色部分移补到左边,这样涂色部分合起来是一个长方形,面积是正方形面积的一半,根据正方形的面积公式S=a2,代入数据计算求解。
【详解】(1)6+6=12(厘米)
12×12-3.14×62
=12×12-3.14×36
=144-113.04
=30.96(平方厘米)
涂色部分的面积是30.96平方厘米。
(2)12×12÷2
=144÷2
=72(平方厘米)
涂色部分的面积是72平方厘米。
19.7.74平方厘米;4平方厘米
【分析】左图:观察图形可知,涂色部分的面积等于正方形的面积减去两个半圆的面积,而两个半圆正好可以组成一个完整的圆,所以用正方形面积减去圆的面积即可;
右图:观察发现,通过割补法,可将左边半圆内的涂色部分移到右边,此时涂色部分组合成一个三角形,三角形的底是右边竖线段的长度4厘米,高是圆的半径4÷2=2(厘米),根据“三角形面积=底×高÷2”算出面积即可。
【详解】左图:6×6=36(平方厘米)
6÷2=3(厘米)
3.14×32=28.26(平方厘米)
36-28.26=7.74(平方厘米)
所以左图涂色部分面积是7.74平方厘米。
右图:4÷2=2(厘米)
4×2÷2=4(平方厘米)
所以右图涂色部分面积是4平方厘米。
【点睛】在解决这类求涂色部分面积的问题时,核心在于把不规则图形转化为规则图形,将复杂问题简单化。左图需要捕捉到两个半圆能拼成一个完整的圆;右图则需要合理割补,将分散的涂色部分重新组合,化零为整,降低计算难度。
20.43.74dm2;25.12dm2
【分析】(1)观察图形,两个完全一样的半圆可以组成一个圆;则涂色部分的面积=长方形的面积-圆的面积,根据长方形的面积公式S=ab,圆的面积公式S=πr2,代入数据计算求解。
(2)观察图形可知,涂色部分的面积=大圆的面积-2个小圆的面积,根据圆的面积公式S=πr2,代入数据计算求解。
【详解】(1)12×6-3.14×(6÷2)2
=12×6-3.14×32
=12×6-3.14×9
=72-28.26
=43.74(dm2)
涂色部分的面积是43.74dm2。
(2)大圆半径:8÷2=4(dm)
小圆半径:8÷4=2(dm)
3.14×42-3.14×22×2
=3.14×16-3.14×4×2
=50.24-25.12
=25.12(dm2)
涂色部分的面积是25.12dm2。
21.12.56
【分析】由图可知,通过旋转涂色半圆可将涂色部分变成半径是4 的圆的,要求涂色部分的面积,可求出半径是4 的圆的面积,再除以4即可。
【详解】3.14×42÷4
=3.14×16÷4
=50.24÷4
=12.56
22.15.25
【分析】涂色部分的面积等于直径为10的半圆的面积减去底为8、高为6的直角三角形的面积,根据圆的面积=圆周率×半径的平方,求出圆的面积,再除以2求出半圆的面积,根据三角形的面积=底×高÷2求出三角形的面积,再用半圆的面积减去三角形的面积即可解答。
【详解】10÷2=5
3.14×52÷2-6×8÷2
=3.14×25÷2-48÷2
=78.5÷2-24
=39.25-24
=15.25
23.5.375
【分析】根据题意可知,每个扇形的半径相当于正方形边长的一半,也就是(5÷2),空白部分的面积可以组合成一个圆的面积,所以阴影部分的面积等于正方形的面积减去圆的面积;根据正方形的面积=边长×边长、圆的面积公式:S=πr2,代入数据分别求出正方形的面积、圆的面积,进而求出阴影部分的面积。
【详解】5÷2=2.5
5×5-3.14×2.52
=5×5-3.14×6.25
=25-19.625
=5.375
阴影部分的面积是5.375。
24.28.26平方厘米
【分析】通过旋转,涂色部分可以拼成圆,涂色部分的面积=圆周率×半径的平方×,据此列式计算。
【详解】3.14×62×
=3.14×36×
=3.14×(36×)
=3.14×9
=28.26(平方厘米)
涂色部分的面积是28.26平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
