湖北省荆州市沙市中学2024-2025学年高二下学期6月月考数学试卷(含解析)
文档属性
| 名称 | 湖北省荆州市沙市中学2024-2025学年高二下学期6月月考数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 639.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览




文档简介
2024—2025学年度下学期2023级6月月考数学试卷
考试时间:2025年6月12日
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设是可导函数,且,则
A.2 B. C. D.
2.某市对机动车单双号限行进行了调查,在参加调查的2748名有车人中有1760名持反对意见,2652名无车人中有1400名持反对意见,在运用这些数据说明“拥有车辆”与“反对机动车单双号限行”是否相关时,用下列哪种方法最有说服力( )
A.平均数 B.方差 C.独立性检验 D.回归直线方程
3.设随机变量X,Y满足:,,则( )
A.4 B.5 C.6 D.7
4.某龙舟队有9名队员,其中3人只会划左舷,4人只会划右舷,2人既会划左舷又会划右舷.现要选派划左舷的3人、右舷的3人共6人去参加比赛,则不同的选派方法共有( )
A.56种 B.68种 C.74种 D.92种
5.已知,则曲线在点处的切线方程为( )
A. B. C. D.
6.的展开式中,所有不含z的项的系数之和为
A.16 B.32 C.27 D.81
7.一只蚂蚁从点A出发沿着水平面的网格线爬行到点B,再由点B沿着长方体的棱爬行至顶点C处,则它可以爬行的不同最短路径条数有
A.40 B.60
C.80 D.120
8.已知,,,则a,b,c的大小关系为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.阳山水蜜桃迄今已有近七十年的栽培历史,产于中国著名桃乡江苏无锡阳山镇.水蜜桃果形大、色泽美,皮韧易剥、香气浓郁,汁多味甜,入口即化,有“水做骨肉”的美誉,阳山水蜜桃早桃品种5月底开始上市,7月15日前后,甜度最高的湖景桃也将大量上市.已知甲、乙两个品种的阳山水蜜桃的质量单位:斤分别服从正态分布,,其正态分布的密度曲线如图所示则下列说法正确的是
A.乙品种水蜜桃的平均质量
B.甲品种水蜜桃的质量比乙类水果的质量更集中于平均值左右
C.甲品种水蜜桃的平均质量比乙类水果的平均质量小
D.乙品种水蜜桃的质量服从的正态分布的参数
10.下列结论中正确的是( )
A. B.
C. D.
11.如图,数轴上的点A,B分别对应实数2,,质点从原点O出发,每次随机地向左或向右移动1个单位长度,移动了4次.以下结论正确的是( )
A.质点移动过程中每次离点O的距离都不超过1个单位长度的概率为
B.质点最终移动到点A的概率为
C.质点在经过点A的条件下,最终回到点O的概率为
D.质点在经过点B的条件下,最终回到点O的概率为
三、填空题:本题共3小题,每小题5分,共15分。
12.某班教室一排有6个座位,如果每个座位只能坐1人,现安排三人就座,恰有两个空位相邻的不同坐法有 种用数字作答
13.在A,B,C三个地区暴发了流感,这三个地区分别有,,人患了流感.假设这三个地区的人口数的比为,现从这三个地区中任取一人,则这个人患流感的概率是 ;如果此人患流感,此人选自A地区的概率 .
14.切比雪夫不等式是19世纪俄国数学家切比雪夫在研究统计规律时发现的,其内容是:对于任一随机变量X,若其数学期望和方差均存在,则对任意正实数,有根据该不等式可以对事件的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号n次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量X,为了至少有的把握使发射信号“1”的频率在区间内,估计信号发射次数n的值至少为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题13分已知一道数学多项选择题有4个选项,其中有3个是正确选项,每选对1个得2分,全选对得满分6分,但是有选错的得0分.学生甲对这4个选项都无法判断是否正确,故其只能猜答案.他有3个方案:猜1个选项猜2个选项猜3个选项.若甲猜每一个选项都是等可能的,请你根据得分期望的大小帮他确定哪一个方案最好.
16.本小题15分红旗淀粉厂2024年之前只生产食品淀粉,下表为年投入资金万元与年收益万元的8组数据:
x 10 20 30 40 50 60 70 80
y 19 23
(1)用模拟生产食品淀粉年收益y与年投入资金x的关系,求出回归方程;
(2)为响应国家“加快调整产业结构”的号召,该企业又自主研发出一种药用淀粉,预计其收益为投入的年该企业计划投入200万元用于生产两种淀粉,求年收益的最大值精确到万元
附:①回归直线中斜率和截距的最小二乘估计公式分别为:
②
161 29 20400 109 603
③,
17.本小题15分设函数,a,,若曲线在点处的切线方程为
(1)求a,b的值;
(2)若关于x的不等式只有唯一实数解,求实数m的值.
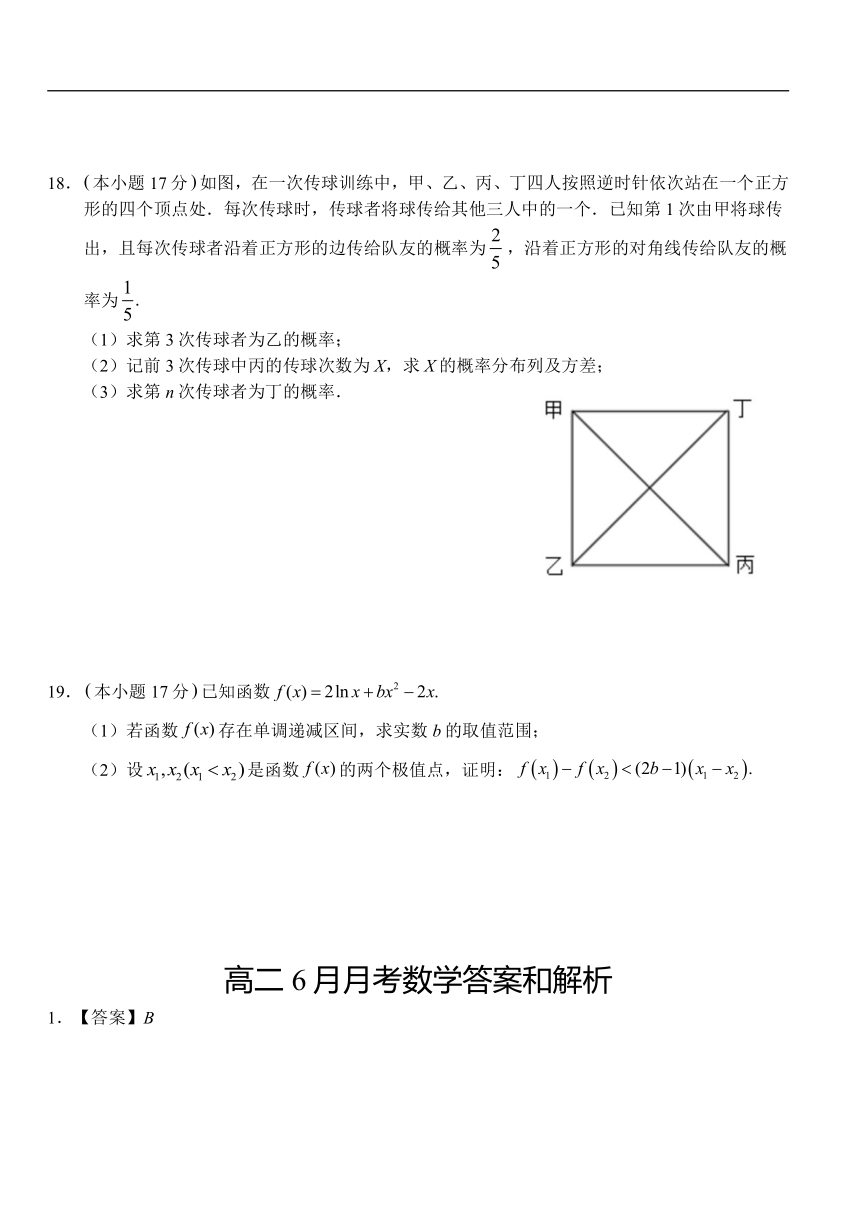
18.本小题17分如图,在一次传球训练中,甲、乙、丙、丁四人按照逆时针依次站在一个正方形的四个顶点处.每次传球时,传球者将球传给其他三人中的一个.已知第1次由甲将球传出,且每次传球者沿着正方形的边传给队友的概率为,沿着正方形的对角线传给队友的概率为
(1)求第3次传球者为乙的概率;
(2)记前3次传球中丙的传球次数为X,求X的概率分布列及方差;
(3)求第n次传球者为丁的概率.
19.本小题17分已知函数
(1)若函数存在单调递减区间,求实数b的取值范围;
(2)设是函数的两个极值点,证明:
高二6月月考数学答案和解析
1.【答案】B
【解答】
解:,
故选
2.【答案】C
【解答】解:在检验两个变量是否相关时,
最有说服力的方法是独立性检验,
故选
3.【答案】A
解:因为,
则,
又,
所以
故选:
4.【答案】D
解:设只会划左舷的3人,只会划右舷的4人,既会划左舷又会划右舷的2人
先分类:以A为标准,划左舷的3人中.
①A中有3人,划右舷的在中选取,有种;
②A中有2人,C中有1人,划右舷的在中剩下的人中选取,有种;
③A中有1人,C中有2人,划右舷的在中剩下的人中选取,有种,
所以共有种,
故选:
5.【答案】B
【解析】解:由于,
则令,可得,
解得,
由,
可得,
令,可得,
解得,
所以曲线在点处的切线方程为,
即
故选:
6.【答案】D
解:由二项式定理知:的展开式的通项为,
若展开式中的项不含z,则,
此时符合条件的项为展开式中的所有项,
令,,
所以的展开式中所有不含z的项的系数之和为
故选
7.【答案】B
解:由题意,从A到B最短路径有条,
由点B沿着置于水平面的长方体的棱爬行至顶点C,最短路径有条,
它可以爬行的不同的最短路径有条
故选
8.【答案】D
【解析】解:,,,
设,则,所以在上单调递增,
则,所以,
则a,b,c的大小关系为
故选:
9.【答案】ABC
解:对于选项A:,故A对;
对于选项B:甲图像相对乙更高瘦,故B对;
对于选项C:,故C对;
对于选项D:乙图像的最高点为,故对称轴时取值为,所以,故D错.
故选
10.【答案】BCD
解:由二项式定理得:,
令得,,
,故A错误;
由二项式定理得:,
令得,,即,
令得,,
,
故B正确;
当且时,由等比数列的求和公式得:
,
根据等号左右两边的展开式中的系数相等,
利用二项式定理得到,故C正确;
由于,
,
根据恒等式等号左右两边的展开式中的系数相等,
利用二项式定理得,
,故D正确.
故选
11.【答案】ABD
【解析】解:选项每次从点O离开,下次必须回到点O,概率为,选项A正确;
选项质点最终移动到点A的概率为,选项B正确;
选项C,由A,B两点关于点O对称可知两个选项的答案相同,
记质点经过点A或点B为事件M,质点最终回到点O为事件N,求条件概率,
从而选项C错误,选项D正确,
故选:
12.【答案】72
解:可看成3个坐着人的座位和3个空座位排队,
因为恰有两个空座位相邻,故和另外两个空座位均不相邻,
先安排3个坐着人的座位,共有种坐法,
产生4个空,然后安排空座位到空中,相邻的两个空座位捆在一起,看作一个元素,有种坐法,
然后再从剩余的3个空中选择两个将空座位安上,因为空座位相同,所以只需要选出1个空位即可,有种坐法,
所以共有种坐法.
故答案为
13.【答案】 ;
【解答】解:设“任取一人,此人患流感”,“此人来自A地区”,“此人来自B地区”,“此人来自C地区”,
,且,,互斥,根据题意有,,,
,,,
根据全概率公式有
由贝叶斯公式有
14.【答案】1250
【解答】
解:由题意知,所以,,
若,则,
即,即,
由切比雪夫不等式可知 ,
要使得至少有的把握使发射信号“1”的频率在区间内,
则,解,
所以估计信号发射次数n的最小值为
故答案为
15.【答案】解:设方案,,的得分分别为随机变量X,Y,Z,
方案:X的所有可能取值为0,2,
,
,
则,
方案:Y的所有可能取值为0,4,
,
,
则,
方案:Z的所有可能取值为0,6,
,
,
则,
,
选择方案最好.
16.【答案】解:有题意得
,
,
所以回归方程为;
设投入x万元生产食品淀粉,万元生产药用淀粉,
所以
,
设,
则,
易得在上单调递增,
上单调递减,
所以
,
又因为,
所以年收益最大值约为万元.
17.【答案】解:由题意得,
所以,
又,
解得
由可得,,
令,解得,
当时,,则为增函数,
当时,,则为减函数,
所以,
所以,
则只有唯一实数解,整理可得,
令,,
则,
因为,
所以恒成立,
令,解得,
当时,,则为减函数,
当时,,则为增函数,
所以,
因为只有唯一实数解使得成立,所以
所以关于x的不等式只有唯一实数解,实数 m的值为
18.【答案】解:甲丙乙的概率为:,
甲丁乙的概率为:,
记事件“第3次传球者为乙”,则
的可能取值为:0,1,
,
,
所以X的概率分布列为
x 0 1
P
设第n次传球者为甲的概率为,第n次传球者为丁的概率为,
则,因为乙和丁相对于甲,地位是相等的,所以第n次传球者为乙的概率也为,
第n次传球者为丙的概率也为,
因为,
所以,因为,
所以是以为首项,为公比的等比数列,
所以,
即
19.【答案】解: ,
函数 存在单调递减区间, 在 上有解,
,设 ,则 ,
当 时,显然 在 上有解;
当 时, , ,设两个根分别为,
由韦达定理知 , ,所以必有一个正根,满足条件.
当 时,有 ,解得 ,综上: .
由题意可知, ,
有两个极值点 , 是 的两个根,则 ,
,
要证 ,即证 ,
即证 ,即证 ,即证 ,
令 ,则证明 ,
令 ,则 , 在 上单调递增,
则 ,即 , 所以原不等式 成立.
考试时间:2025年6月12日
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设是可导函数,且,则
A.2 B. C. D.
2.某市对机动车单双号限行进行了调查,在参加调查的2748名有车人中有1760名持反对意见,2652名无车人中有1400名持反对意见,在运用这些数据说明“拥有车辆”与“反对机动车单双号限行”是否相关时,用下列哪种方法最有说服力( )
A.平均数 B.方差 C.独立性检验 D.回归直线方程
3.设随机变量X,Y满足:,,则( )
A.4 B.5 C.6 D.7
4.某龙舟队有9名队员,其中3人只会划左舷,4人只会划右舷,2人既会划左舷又会划右舷.现要选派划左舷的3人、右舷的3人共6人去参加比赛,则不同的选派方法共有( )
A.56种 B.68种 C.74种 D.92种
5.已知,则曲线在点处的切线方程为( )
A. B. C. D.
6.的展开式中,所有不含z的项的系数之和为
A.16 B.32 C.27 D.81
7.一只蚂蚁从点A出发沿着水平面的网格线爬行到点B,再由点B沿着长方体的棱爬行至顶点C处,则它可以爬行的不同最短路径条数有
A.40 B.60
C.80 D.120
8.已知,,,则a,b,c的大小关系为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.阳山水蜜桃迄今已有近七十年的栽培历史,产于中国著名桃乡江苏无锡阳山镇.水蜜桃果形大、色泽美,皮韧易剥、香气浓郁,汁多味甜,入口即化,有“水做骨肉”的美誉,阳山水蜜桃早桃品种5月底开始上市,7月15日前后,甜度最高的湖景桃也将大量上市.已知甲、乙两个品种的阳山水蜜桃的质量单位:斤分别服从正态分布,,其正态分布的密度曲线如图所示则下列说法正确的是
A.乙品种水蜜桃的平均质量
B.甲品种水蜜桃的质量比乙类水果的质量更集中于平均值左右
C.甲品种水蜜桃的平均质量比乙类水果的平均质量小
D.乙品种水蜜桃的质量服从的正态分布的参数
10.下列结论中正确的是( )
A. B.
C. D.
11.如图,数轴上的点A,B分别对应实数2,,质点从原点O出发,每次随机地向左或向右移动1个单位长度,移动了4次.以下结论正确的是( )
A.质点移动过程中每次离点O的距离都不超过1个单位长度的概率为
B.质点最终移动到点A的概率为
C.质点在经过点A的条件下,最终回到点O的概率为
D.质点在经过点B的条件下,最终回到点O的概率为
三、填空题:本题共3小题,每小题5分,共15分。
12.某班教室一排有6个座位,如果每个座位只能坐1人,现安排三人就座,恰有两个空位相邻的不同坐法有 种用数字作答
13.在A,B,C三个地区暴发了流感,这三个地区分别有,,人患了流感.假设这三个地区的人口数的比为,现从这三个地区中任取一人,则这个人患流感的概率是 ;如果此人患流感,此人选自A地区的概率 .
14.切比雪夫不等式是19世纪俄国数学家切比雪夫在研究统计规律时发现的,其内容是:对于任一随机变量X,若其数学期望和方差均存在,则对任意正实数,有根据该不等式可以对事件的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号n次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量X,为了至少有的把握使发射信号“1”的频率在区间内,估计信号发射次数n的值至少为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题13分已知一道数学多项选择题有4个选项,其中有3个是正确选项,每选对1个得2分,全选对得满分6分,但是有选错的得0分.学生甲对这4个选项都无法判断是否正确,故其只能猜答案.他有3个方案:猜1个选项猜2个选项猜3个选项.若甲猜每一个选项都是等可能的,请你根据得分期望的大小帮他确定哪一个方案最好.
16.本小题15分红旗淀粉厂2024年之前只生产食品淀粉,下表为年投入资金万元与年收益万元的8组数据:
x 10 20 30 40 50 60 70 80
y 19 23
(1)用模拟生产食品淀粉年收益y与年投入资金x的关系,求出回归方程;
(2)为响应国家“加快调整产业结构”的号召,该企业又自主研发出一种药用淀粉,预计其收益为投入的年该企业计划投入200万元用于生产两种淀粉,求年收益的最大值精确到万元
附:①回归直线中斜率和截距的最小二乘估计公式分别为:
②
161 29 20400 109 603
③,
17.本小题15分设函数,a,,若曲线在点处的切线方程为
(1)求a,b的值;
(2)若关于x的不等式只有唯一实数解,求实数m的值.
18.本小题17分如图,在一次传球训练中,甲、乙、丙、丁四人按照逆时针依次站在一个正方形的四个顶点处.每次传球时,传球者将球传给其他三人中的一个.已知第1次由甲将球传出,且每次传球者沿着正方形的边传给队友的概率为,沿着正方形的对角线传给队友的概率为
(1)求第3次传球者为乙的概率;
(2)记前3次传球中丙的传球次数为X,求X的概率分布列及方差;
(3)求第n次传球者为丁的概率.
19.本小题17分已知函数
(1)若函数存在单调递减区间,求实数b的取值范围;
(2)设是函数的两个极值点,证明:
高二6月月考数学答案和解析
1.【答案】B
【解答】
解:,
故选
2.【答案】C
【解答】解:在检验两个变量是否相关时,
最有说服力的方法是独立性检验,
故选
3.【答案】A
解:因为,
则,
又,
所以
故选:
4.【答案】D
解:设只会划左舷的3人,只会划右舷的4人,既会划左舷又会划右舷的2人
先分类:以A为标准,划左舷的3人中.
①A中有3人,划右舷的在中选取,有种;
②A中有2人,C中有1人,划右舷的在中剩下的人中选取,有种;
③A中有1人,C中有2人,划右舷的在中剩下的人中选取,有种,
所以共有种,
故选:
5.【答案】B
【解析】解:由于,
则令,可得,
解得,
由,
可得,
令,可得,
解得,
所以曲线在点处的切线方程为,
即
故选:
6.【答案】D
解:由二项式定理知:的展开式的通项为,
若展开式中的项不含z,则,
此时符合条件的项为展开式中的所有项,
令,,
所以的展开式中所有不含z的项的系数之和为
故选
7.【答案】B
解:由题意,从A到B最短路径有条,
由点B沿着置于水平面的长方体的棱爬行至顶点C,最短路径有条,
它可以爬行的不同的最短路径有条
故选
8.【答案】D
【解析】解:,,,
设,则,所以在上单调递增,
则,所以,
则a,b,c的大小关系为
故选:
9.【答案】ABC
解:对于选项A:,故A对;
对于选项B:甲图像相对乙更高瘦,故B对;
对于选项C:,故C对;
对于选项D:乙图像的最高点为,故对称轴时取值为,所以,故D错.
故选
10.【答案】BCD
解:由二项式定理得:,
令得,,
,故A错误;
由二项式定理得:,
令得,,即,
令得,,
,
故B正确;
当且时,由等比数列的求和公式得:
,
根据等号左右两边的展开式中的系数相等,
利用二项式定理得到,故C正确;
由于,
,
根据恒等式等号左右两边的展开式中的系数相等,
利用二项式定理得,
,故D正确.
故选
11.【答案】ABD
【解析】解:选项每次从点O离开,下次必须回到点O,概率为,选项A正确;
选项质点最终移动到点A的概率为,选项B正确;
选项C,由A,B两点关于点O对称可知两个选项的答案相同,
记质点经过点A或点B为事件M,质点最终回到点O为事件N,求条件概率,
从而选项C错误,选项D正确,
故选:
12.【答案】72
解:可看成3个坐着人的座位和3个空座位排队,
因为恰有两个空座位相邻,故和另外两个空座位均不相邻,
先安排3个坐着人的座位,共有种坐法,
产生4个空,然后安排空座位到空中,相邻的两个空座位捆在一起,看作一个元素,有种坐法,
然后再从剩余的3个空中选择两个将空座位安上,因为空座位相同,所以只需要选出1个空位即可,有种坐法,
所以共有种坐法.
故答案为
13.【答案】 ;
【解答】解:设“任取一人,此人患流感”,“此人来自A地区”,“此人来自B地区”,“此人来自C地区”,
,且,,互斥,根据题意有,,,
,,,
根据全概率公式有
由贝叶斯公式有
14.【答案】1250
【解答】
解:由题意知,所以,,
若,则,
即,即,
由切比雪夫不等式可知 ,
要使得至少有的把握使发射信号“1”的频率在区间内,
则,解,
所以估计信号发射次数n的最小值为
故答案为
15.【答案】解:设方案,,的得分分别为随机变量X,Y,Z,
方案:X的所有可能取值为0,2,
,
,
则,
方案:Y的所有可能取值为0,4,
,
,
则,
方案:Z的所有可能取值为0,6,
,
,
则,
,
选择方案最好.
16.【答案】解:有题意得
,
,
所以回归方程为;
设投入x万元生产食品淀粉,万元生产药用淀粉,
所以
,
设,
则,
易得在上单调递增,
上单调递减,
所以
,
又因为,
所以年收益最大值约为万元.
17.【答案】解:由题意得,
所以,
又,
解得
由可得,,
令,解得,
当时,,则为增函数,
当时,,则为减函数,
所以,
所以,
则只有唯一实数解,整理可得,
令,,
则,
因为,
所以恒成立,
令,解得,
当时,,则为减函数,
当时,,则为增函数,
所以,
因为只有唯一实数解使得成立,所以
所以关于x的不等式只有唯一实数解,实数 m的值为
18.【答案】解:甲丙乙的概率为:,
甲丁乙的概率为:,
记事件“第3次传球者为乙”,则
的可能取值为:0,1,
,
,
所以X的概率分布列为
x 0 1
P
设第n次传球者为甲的概率为,第n次传球者为丁的概率为,
则,因为乙和丁相对于甲,地位是相等的,所以第n次传球者为乙的概率也为,
第n次传球者为丙的概率也为,
因为,
所以,因为,
所以是以为首项,为公比的等比数列,
所以,
即
19.【答案】解: ,
函数 存在单调递减区间, 在 上有解,
,设 ,则 ,
当 时,显然 在 上有解;
当 时, , ,设两个根分别为,
由韦达定理知 , ,所以必有一个正根,满足条件.
当 时,有 ,解得 ,综上: .
由题意可知, ,
有两个极值点 , 是 的两个根,则 ,
,
要证 ,即证 ,
即证 ,即证 ,即证 ,
令 ,则证明 ,
令 ,则 , 在 上单调递增,
则 ,即 , 所以原不等式 成立.
同课章节目录
