【期末提升讲义】专题五:长方形和正方形的面积-2024-2025学年三年级数学下册北京版
文档属性
| 名称 | 【期末提升讲义】专题五:长方形和正方形的面积-2024-2025学年三年级数学下册北京版 |
|
|
| 格式 | docx | ||
| 文件大小 | 432.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 00:00:00 | ||
图片预览





文档简介
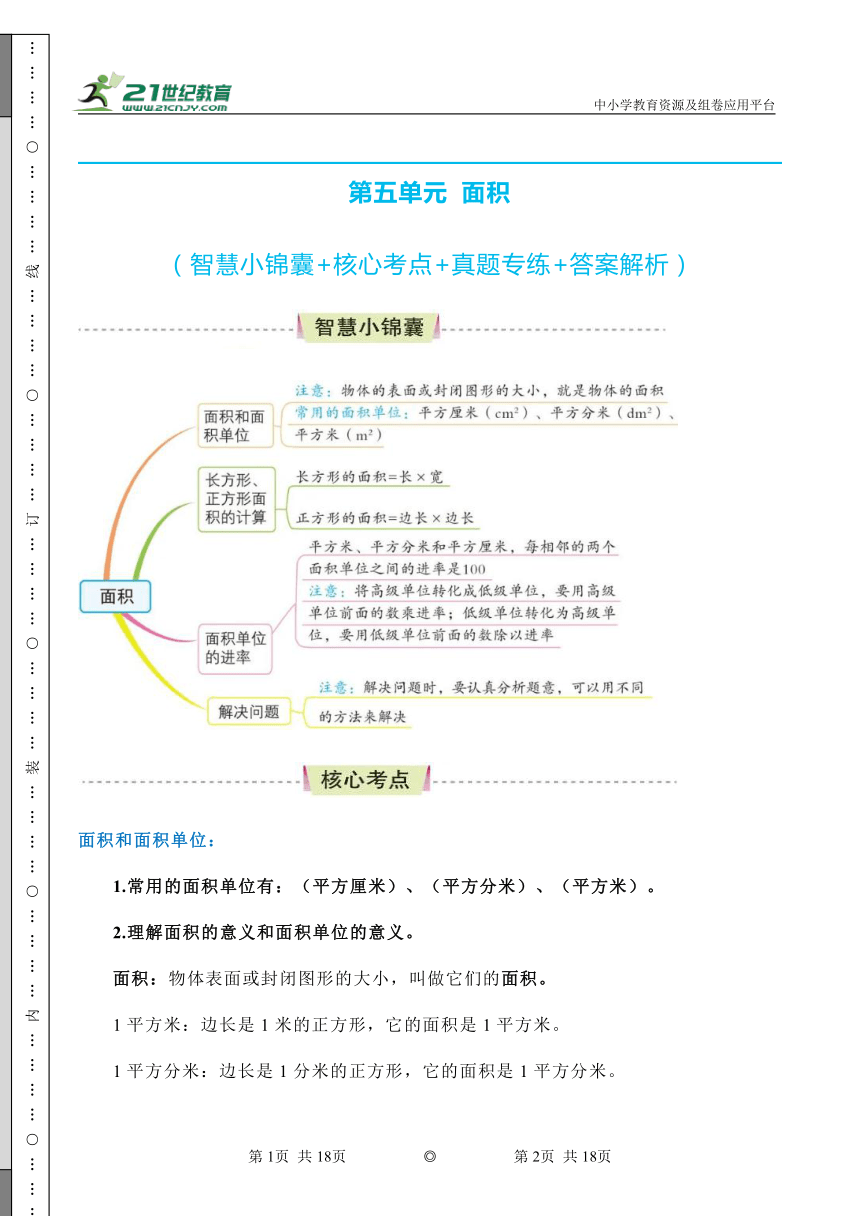
第五单元 面积
(智慧小锦囊+核心考点+真题专练+答案解析)
面积和面积单位:
1.常用的面积单位有:(平方厘米)、(平方分米)、(平方米)。
2.理解面积的意义和面积单位的意义。
面积:物体表面或封闭图形的大小,叫做它们的面积。
1平方米:边长是1米的正方形,它的面积是1平方米。
1平方分米:边长是1分米的正方形,它的面积是1平方分米。
1平方厘米:边长是1厘米的正方形,它的面积是1平方厘米。
3.在生活中找出接近于1平方厘米、1平方分米、1平方米的例子。例如1平方厘米(指甲盖)、1平方分米(电脑光盘或电线插座)、1平方米(教室侧面的小展板)。
4.区分长度单位和面积单位的不同。长度单位测量线段的长短,面积单位测量面的大小。
5.比较两个图形面积的大小,要用(统一)的面积单位来测量。
背 熟 :
(1)边长(1厘米)的正方形,面积是(1平方厘米)。
(反过来也要会说。面积是1平方厘米的正方形,它的边长是1厘米。)
(2)边长 (1分米)的正方形,面积是(1平方分米)。
(3)边长 (1米 )的正方形,面积是(1平方米)。
(4)边长是(100米)的正方形面积是(1公顷),也就是(10000平方米)。
(5)边长是(1千米)的正方形面积是1平方千米。
面积单位进率和土地面积单位:
1.常用的土地面积单位有( 公顷 )和( 平方千米 )。
★“ 公顷 ”→ 测量菜地面积、果园面积、建筑面积
★“ 平方千米 ”→ 测量城市土地面积、国家面积
1公顷:边长是100米的正方形,它的面积是1公顷。
1平方千米:边长是1千米的正方形,它的面积是1平方千米。
1公顷=10000平方米
1平方千米=100公顷
1平方千米=1000000平方米
2.正确理解并熟记相邻的面积单位之间的进率。
① 进率100:
1平方米 = 100平方分米
1平方分米 = 100平方厘米
1平方千米 = 100 公顷
② 进率10000:
1公顷 = 10000平方米
1平方米 = 10000平方厘米
③ 进率1000000:
1平方千米 = 1000000平方米
④ 相邻两个常用的长度单位之间的进率是( 10 )。
相邻两个常用的面积单位之间的进率是( 100 )。
背熟公式
1、周长公式:
长方形的周长 = (长+宽)× 2
长 = 周长÷2-宽
或者:(周长-长×2)÷2= 宽
宽 = 周长÷2-长
或者:(周长-宽×2)÷2=长
正方形的周长 = 边长×4
正方形的边长 = 周长÷4
2、面积公式:
长方形的面积=长×宽 正方形的面积=边长×边长 长方形的周长=(长+宽)×2 正方形的周长=边长×4 已知面积求长:长=面积÷宽 已知面积求边长:边长=面积开平方 已知周长求长:长=周长÷2 - 宽 已知面积求边长:边长=面积÷4
A、正确区分长方形和正方形的周长和面积的意义,并能正确运用上面的4个计算公式求周长和面积。
归类:什么样的问题是求周长?(缝花边、围栅栏、围栏杆、池塘或花坛周围小路长度、围操场跑步的长度等等)什么样的问题是求面积?或与面积有关?(课本等封面大小、刷墙、花坛周围小路面积、给餐桌配玻璃、给课桌配桌布、洒水车洒到的地面、某物品占地面积、买玻璃、买镜子、买布、买地毯、铺地、裁手帕的等等)
B、长方形或正方形纸的剪或拼。有两个或两个以上长方形或正方形拼成新的图形后的面积与周长。从一个图形中(通常是长方形)剪掉一个图形(最大的正方形等)求剪掉部分的面积或周长、求剩下部分的面积或周长。要求先画图,再标上所用数据,最后列式计算。
C、刷墙的(有的中间有黑板、窗户等):用大面积-小面积。
熟练运用进率进行面积单位之间的换算。掌握换算的方法。
1、低级单位——高级单位:数量÷它们间的进率
如:零钱换大钱,张数减少;300平方分米=3平方米
1、高级单位——低级单位:数量×们间的进率
如:大钱换零钱,张数增多;5平方千米=500公顷
注 意:
(1) 面积相等的两个图形,周长不一定相等。
周长相等的两个图形,面积不一定相等。
(2) 大单位换算小单位(乘它们之间的进率)
小单位换算大单位(除以它们之间的进率)
(3) 长度单位和面积单位的单位不同,无法比较。
(4)周长相等的两个长方形,面积不一定相等。面积相等的两个长方形,周长也不一定相等。
一、选择题
1.一个长方形的面积为6000平方分米,宽是4米,这个长方形的长是( )米。
A.150 B.15 C.25 D.250
2.学校操场面积为4000( ).
A.米 B.平方分米 C.平方米 D.平方厘米
3.边长1米的正方形,面积是( ),周长是( )。
A.1平方米;1米 B.1平方米;4米
C.4平方米;4米 D.4平方米;1米
4.以下( )的占地面积大约是45平方米.
A.1块黑板的面积 B.1间教室的占地面积
C.延庆区的占地面积 D.1个操场的占地面积
5.下图中每个小正方形的边长是1厘米,这个大正方形的面积是( )。
A.4厘米 B.16厘米 C.4平方厘来 D.16平方厘米
二、填空题
6.一个长方形周长24厘米,长与宽各增加5厘米,面积增加 平方厘米.
7.估计如图图形的面积大约各是多少平方厘米。(每个小方格表示1cm2)
约( )平方厘米 约( )平方厘米
8.在( )里填上“>”“<”或“=”.
2000平方分米( )1900平方米 3平方米( )30000平方厘米
500平方分米( )5平方米 4000平方米( )4000平方分米
70平方分米( )7平方米 500平方厘米( )60平方分米
9.填上适当的单位名称:上海市的面积大约是6340( )。
10.想一想,填一填。
(1)边长是( )分米的正方形,面积是1平方分米。
(2)边长是( )米的正方形,面积是1平方米。
(3)边长是( )厘米的正方形,面积是1平方厘米。
11.一块长方形的住宅用地,长12米,宽75米,这块住宅用地有 公顷.
12.大洋小学占地面积是9500( ).
13.边长分别是1米、1分米、1厘米的三个正方形中,面积最大的是边长为1 的正方形.
14.下图由小方格(每个小方格的面积是1平方厘米)围成的空白部分的周长是( )厘米,面积是( )平方厘米。
15.王大伯在自家的一面墙建一个鸡舍,想用12米长的竹篱笆围出最大的鸡舍,仔细想想,怎样建鸡舍的面积最大,面积是 平方米.
16.铅笔盒宽10( );数学课本长19( );课桌高7( );一个纽扣的面积大约是1( );一块橡皮的面积是8( );一支钢笔长13( );学校操场的面积是720( );一棵大树高12( );一张邮票的面积是4( ).
17.一个长方形花园的长是15米,宽是12米,这个花园的面积是 平方米。若把这个花园用篱笆围起来,至少需要 米长的篱笆。
三、判断题
18.1000平方厘米>20平方分米。( )
19.一个蓄水池深4.5米、长40米、宽30米,这个蓄水池的占地面积是1200平方米。( )
20.一个正方形边长是4分米,这个正方形的面积和周长相等. .(判断对错)
21.边长4米的正方形,它的周长和面积相等。( )
22.100公顷=1平方千米. .(判断对错)
四、解答题
23.长方形暖棚的长为22米,宽为14米,每平方米种6棵果苗.这个暖棚里一共可以种这样的果苗多少棵?
24.两块长方形花圃的长相等,第二块面积是多少?
25.一个长方形操场,长是82.4米,宽是41米.
26.涂色的正方形周长是60厘米(如图),求正方形的面积是多少?
27.一块正方形果园的四周围上了长68米的篱笆,这块正方形果园的面积是多少平方米?
28.一幅风景画长50厘米,宽40厘米,它的面积是多少平方厘米?
29.学校有一块长方形草地,如果把它的长缩短20米,这块草地就变成了边长是80米的正方形草地。原来这块长方形草地的面积是多少平方米?
先画图分析:
再列式解答:
30.用一根20米长的绳子,围一块长方形或正方形的绿地.小明用表格进行了探索.你发现了什么?
长(m ) 宽(m ) 面积(m )
9 1 9
8 2 16
7 3 21
6 4 24
5 5 25
我发现了:
31.长方形草坪的长是30米,面积是450平方米.扩建后宽没变,长增加到150米,面积会变成多少?
32.一块长方形苗圃的宽是7米,面积是238平方米,如果这个苗圃的长不变,宽增加到21米,扩大后的苗圃面积是多少平方米?
33.一个长方形,如果长和宽各增加8厘米,那么面积就增加384平方厘米.如果长和宽再各增加8厘米,那么面积又会增加多少平方厘米?
中小学教育资源及组卷应用平台 (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台 (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】平方分米和平方米之间的进率是100,据此将长方形的面积换算成平方米,再根据长方形的长=面积÷宽,把数据代入公式解答。
【详解】6000平方分米=60平方米
60÷4=15(米)
长是15米。
故答案为:B
【点睛】本题考查查长方形面积公式的灵活运用和面积单位的换算,关键是熟记公式。
2.C
【详解】略
3.B
【分析】根据正方形的面积公式,周长公式计算即可。
【详解】面积:1×1=1平方米;周长:1×4=4米。
故答案为:B
【点睛】熟悉正方形面积公式、周长公式是解答此题的关键。
4.B
【详解】略
5.D
【分析】观察上图可知,大正方形的边长为4厘米,4乘4即等于大正方形的面积,据此即可解答。
【详解】4×4=16(平方厘米)
故答案为:D
【点睛】明确大正方形的边长是多少是解答本题的关键。
6.85
【详解】试题分析:如图所示,增加的部分由①、②、③组成,设长方形的长为a,宽为b,则①的长为a,宽为5厘米,②的边长为5厘米,③的长为b,宽为5厘米,于是可以分别利用长方形和正方形的面积公式,表示出这三个图形的面积,再据“一个长方形周长24厘米”求出长和宽的和,即可求解.
解:设长方形的长为a,宽为b,
长和宽的和:a+b=24÷2=12(厘米),
增加部分的面积:
5a+5×5+5b,
=5(a+b)+25,
=5×12+25,
=60+25,
=85(平方厘米);
答:面积增加85平方厘米.
故答案为85.
点评:解答此题的关键是:弄清楚增加部分由哪些图形组成.
7. 8 12
【分析】左图可以看作一个长3厘米、宽2厘米的长方形的面积,再加上超出长方形面积范围的部分大约2格的面积;
右图可以看作一个长4厘米、宽3厘米的长方形的面积,据此解答。
【详解】左图:3×2+2
=6+2
=8(平方厘米)
右图:4×3=12(平方厘米)
(答案不唯一)
【点睛】解答此题,要注意认真分析图形,弄清图形所占的方格数是解答此题的关键。
8. < = = > < <
【详解】2000平方分米=20平方米 20平方米<1900平方米
3平方米=300平方分米=30000平方厘米
100平方分米=1平方米 500平方分米=5平方米
4000平方米=400000平方分米 400000平方分米 >4000平方分米
7平方米=700平方分米 70平方分米<7平方米
500平方厘米=5平方分米 5平方分米<60平方分米
9.平方千米
【分析】根据生活经验以及对面积单位和数据大小的认识,结合实际情况可知:计量上海市的面积用“平方千米”作单位。
【详解】上海市的面积大约是6340平方千米。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
10.(1)1
(2)1
(3)1
【详解】(1)边长是1分米的正方形,面积是1平方分米。生活中,经常能够接触到1平方分米大小的物品,如粉笔盒正面的面积大约是1平方分米,家里的肥皂盒大约是1平方分米那么大。
(2)边长是1米的正方形,面积是1平方米。教师的讲桌桌面大约是1平方米那么大。
(3)边长是1厘米的正方形,面积是1平方厘米。大拇指的指甲盖、骰子的每个面、电脑键盘上的按键等的大小都大约是1平方厘米。
11.0.09
【详解】试题分析:要求这块住宅用地的公顷数,就是求它的面积,利用面积=长×宽算出面积,再把平方米数换算成公顷数,用平方米数除以进率10000即可.
解:这块住宅用地的面积:12×75=900(平方米),
900平方米=0.09公顷.
答:这块住宅用地有0.09公顷.
故答案为0.09.
点评:此题考查长方形面积的计算方法和面积单位间的换算.
12.平方米
【解析】略
13.米
【详解】考虑长度,最长是的1米,所有边长为1米的正方形面积最大
【分析】联系实际
14. 20 21
【分析】根据“每个小方格的面积是1平方厘米”可知,每小格的边长是1厘米;所以空白部分的长是7厘米、宽是3厘米,再根据长方形面积=长×宽、长方形周长=(长+宽)×2,计算出长方形的面积和周长即可。
【详解】空白部分是一个长7厘米、宽3厘米的长方形,
(7+3)×2
=10×2
=20(厘米)
7×3=21(平方厘米)
所以,空白部分的周长是20厘米,面积是21平方厘米。
【点睛】确定空白部分的长与宽的长度是解题关键。
15.16
【详解】试题分析:由题意可知,围成一个正方形,则面积就最大,依据篱笆长度已知,即可求出正方形的边长,从而求出鸡舍的面积.
解:12÷3=4(米),
4×4=16(平方米);
答:将鸡舍围成一个正方形其面积最大,面积是16平方米.
故答案为16.
点评:解答此题的关键是明白:围成正方形面积最大,要注意篱笆只围三面.
16. 厘米 厘米 分米 平方厘米 平方厘米 厘米 平方米 米 平方厘米
【详解】区分长度单位和面积单位,常用的长度单位有米、分米、厘米,常用的面积单位有平方米、平方分米、平方厘米.
17. 180 54
【分析】长方形的面积=长×宽;长方形的周长=(长+宽)×2。
【详解】15×12=180(平方米);(15+12)×2=54(米)
故答案为:180;54。
18.×
【分析】平方厘米和平方分米之间的进率是100,据此解答即可。
【详解】1000平方厘米=10平方分米
10平方分米<20平方分米
1000平方厘米<20平方分米
故答案为:×
【点睛】本题考查面积单位的换算。把低级单位换算成高级单位,就除以单位间的进率;把高级单位换算成低级单位,就乘单位间的进率。
19.√
【分析】根据长方形的面积=长×宽,把数据代入公式求出这个水池的占地面积与1200平方米进行比较,如果占地面积等于1200平方米,此说法是正确的,否则是错误的。据此判断。
【详解】40×30=1200(平方米)
故题干说法正确。
故答案为:√
【点睛】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
20.×
【详解】试题分析:根据正方形的周长、面积的意义,正方形的周长是指围成这个正方形的4条边的长度和;正方形的面积是指围成平面的大小;因为周长和面积不是同类量所以不能进行比较.据此判断.
解答:解:正方形的周长是指围成这个正方形的4条边的长度和;正方形的面积是指围成平面的大小;
因为周长和面积不是同类量所以不能进行比较.
所以一个正方形边长是4分米,这个正方形的面积和周长相等.这种说法是错误的.
故答案为×.
点评:此题考查的目的是理解掌握周长、面积的意义,明确:只有同类量才能比较大小.
21.×
【分析】
封闭图形一周的长度,是它的周长;物体的表面或围成的平面图形的大小,叫面积。根据周长、面积的意义可知,因为周长和面积是不同的两个量,所以无法比较。
【详解】
正方形的周长是指围成正方形四条边的总长度,正方形的面积是指围成正方形的大小,意义不同;
正方形的周长是边长×4,正方形的面积是边长×边长,计算方法不同;
周长的计量单位是长度单位,面积的计量单位是面积单位,计量单位不同;
故无法比较,所以原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握周长、面积的意义及应用。周长和面积是不同的两个量,无法比较大小。
22.√
【详解】试题分析:根据面积单位公顷与平方千米之间的关系,1平方千米=100公顷.
解答:解:100公顷=1平方千米.
故答案为√.
点评:本题是考查面积单位平方千米与公顷之间的进率,属于基础知识,要记住.
23.1848棵
【详解】试题分析:先利用长方形的面积公式求出暖棚的面积,再乘每平方米种的果苗的棵数,即可得解.
解:22×14×6,
=308×6,
=1848(棵),
答:这个暖棚里一共可以种这样的果苗1848棵.
点评:此题主要考查长方形的面积的计算方法在实际生活中的应用.
24.744平方米
【分析】根据长方形的面积公式S=ab,得出a=S÷b,求出第一块长方形花圃的长,即第二块长方形花圃的长,再利用长方形的面积公式求出第二块花圃的面积.
【详解】248÷7×21
=×21
=744(平方米)
答:第二块的面积是744平方米.
25.3378.4
【详解】试题分析:根据长方形的面积公式:s=ab,把数据代入公式解答即可.
解:82.4×41=3378.4(平方米),
答:这个操场的面积是3378.4平方米.
点评:此题主要考查长方形的面积公式的灵活运用.
26.225平方米
【分析】根据正方形周长公式用周长除以4即可求出正方形的边长,用边长乘边长即可求出正方形的面积。
【详解】(60÷4)×(60÷4)
=15×15
=225(平方米)
答:正方形的面积是225平方米。
【点睛】本题主要考查学生对正方形的周长和面积公式的掌握及灵活运用。
27.果园的面积是289平方米
【详解】试题分析:先根据正方形的周长公式求出这个正方形果园的边长,再利用正方形的面积=边长×边长计算即可解答.
解:68÷4=17(米),
17×17=289(平方米),
答:果园的面积是289平方米.
点评:此题考查正方形的周长与面积公式的计算应用,熟记公式即可解答.
28.2000平方厘米.
【详解】试题分析:长方形的面积=长×宽,长和宽已知,代入公式即可求解.
解:50×40=2000(平方厘米);
答:这幅风景画的面积是2000平方厘米.
【点评】此题主要考查长方形的面积的计算方法.
29.;8000平方米。
【分析】先画出图形,因为长缩短20米以后是边长为80米的正方形,那么原来长方形的长就为100米,宽为80米,再根据长方形面积=长×宽,求出原来长方形草地面积即可。
【详解】
(80+20)×80
=100×80
=8000(平方米)
答:原来这块长方形草地的面积是8000平方米
【点睛】本题考查的是长方形的面积,关键是要将原来长方形的长求出来。
30.我发现了:长方形的周长相同时,长与宽越接近,长方形的面积越大。
【详解】略
31.2250平方米
【详解】试题分析:先根据长方形草坪原来的面积求出草坪的宽是450÷30=15(米),再利用长方形的面积=长×宽即可求出扩建后的面积.
解:450÷30×150,
=15×150,
=2250(平方米),
答:面积是2250平方米.
点评:此题考查长方形的面积公式的计算应用,关键是明确草坪的宽.
32.714平方米
【详解】试题分析:根据题意,可依据原来长方形面积除以宽计算出长方形的长,宽增加到21米,即宽为21米,根据长方形的面积公式进行计算即可得到答案.
解:长方形的长:238÷7=34(米),
扩大后的面积为:34×21=714(平方米);
答:扩大后的苗圃面积是714平方米.
点评:解答此题的关键是根据原来的长方形的面积计算出长方形的长,然后再依据长方形的面积公式进行计算即可.
33.512平方厘米
【详解】试题分析:如图:增加部分是面积是384平方厘米,先用“384﹣8×8=320平方厘米”求出增加的两个长方形的面积的和,因为这两个长方形都有一条边是8,所以原来长宽的和为:320÷8=40厘米;第二次增加后的长宽和为:40+8×2=56厘米,增加的面积:56×8+8×8=512平方厘米;进而得出结论.
解:如图:[(384﹣8×8)÷8+8×2]×8+8×8,
=[40+16]×8+64,
=512(平方厘米);
答:面积又会增加512平方厘米.
点评:此题较难,解答此题的关键:求出长方形的长和宽的和,进而找出长方形的长和宽的和、增加的长和宽的长度和增加的面积三者之间的关系,是解答此题的关键所在.
答案第1页,共2页
答案第1页,共2页
(智慧小锦囊+核心考点+真题专练+答案解析)
面积和面积单位:
1.常用的面积单位有:(平方厘米)、(平方分米)、(平方米)。
2.理解面积的意义和面积单位的意义。
面积:物体表面或封闭图形的大小,叫做它们的面积。
1平方米:边长是1米的正方形,它的面积是1平方米。
1平方分米:边长是1分米的正方形,它的面积是1平方分米。
1平方厘米:边长是1厘米的正方形,它的面积是1平方厘米。
3.在生活中找出接近于1平方厘米、1平方分米、1平方米的例子。例如1平方厘米(指甲盖)、1平方分米(电脑光盘或电线插座)、1平方米(教室侧面的小展板)。
4.区分长度单位和面积单位的不同。长度单位测量线段的长短,面积单位测量面的大小。
5.比较两个图形面积的大小,要用(统一)的面积单位来测量。
背 熟 :
(1)边长(1厘米)的正方形,面积是(1平方厘米)。
(反过来也要会说。面积是1平方厘米的正方形,它的边长是1厘米。)
(2)边长 (1分米)的正方形,面积是(1平方分米)。
(3)边长 (1米 )的正方形,面积是(1平方米)。
(4)边长是(100米)的正方形面积是(1公顷),也就是(10000平方米)。
(5)边长是(1千米)的正方形面积是1平方千米。
面积单位进率和土地面积单位:
1.常用的土地面积单位有( 公顷 )和( 平方千米 )。
★“ 公顷 ”→ 测量菜地面积、果园面积、建筑面积
★“ 平方千米 ”→ 测量城市土地面积、国家面积
1公顷:边长是100米的正方形,它的面积是1公顷。
1平方千米:边长是1千米的正方形,它的面积是1平方千米。
1公顷=10000平方米
1平方千米=100公顷
1平方千米=1000000平方米
2.正确理解并熟记相邻的面积单位之间的进率。
① 进率100:
1平方米 = 100平方分米
1平方分米 = 100平方厘米
1平方千米 = 100 公顷
② 进率10000:
1公顷 = 10000平方米
1平方米 = 10000平方厘米
③ 进率1000000:
1平方千米 = 1000000平方米
④ 相邻两个常用的长度单位之间的进率是( 10 )。
相邻两个常用的面积单位之间的进率是( 100 )。
背熟公式
1、周长公式:
长方形的周长 = (长+宽)× 2
长 = 周长÷2-宽
或者:(周长-长×2)÷2= 宽
宽 = 周长÷2-长
或者:(周长-宽×2)÷2=长
正方形的周长 = 边长×4
正方形的边长 = 周长÷4
2、面积公式:
长方形的面积=长×宽 正方形的面积=边长×边长 长方形的周长=(长+宽)×2 正方形的周长=边长×4 已知面积求长:长=面积÷宽 已知面积求边长:边长=面积开平方 已知周长求长:长=周长÷2 - 宽 已知面积求边长:边长=面积÷4
A、正确区分长方形和正方形的周长和面积的意义,并能正确运用上面的4个计算公式求周长和面积。
归类:什么样的问题是求周长?(缝花边、围栅栏、围栏杆、池塘或花坛周围小路长度、围操场跑步的长度等等)什么样的问题是求面积?或与面积有关?(课本等封面大小、刷墙、花坛周围小路面积、给餐桌配玻璃、给课桌配桌布、洒水车洒到的地面、某物品占地面积、买玻璃、买镜子、买布、买地毯、铺地、裁手帕的等等)
B、长方形或正方形纸的剪或拼。有两个或两个以上长方形或正方形拼成新的图形后的面积与周长。从一个图形中(通常是长方形)剪掉一个图形(最大的正方形等)求剪掉部分的面积或周长、求剩下部分的面积或周长。要求先画图,再标上所用数据,最后列式计算。
C、刷墙的(有的中间有黑板、窗户等):用大面积-小面积。
熟练运用进率进行面积单位之间的换算。掌握换算的方法。
1、低级单位——高级单位:数量÷它们间的进率
如:零钱换大钱,张数减少;300平方分米=3平方米
1、高级单位——低级单位:数量×们间的进率
如:大钱换零钱,张数增多;5平方千米=500公顷
注 意:
(1) 面积相等的两个图形,周长不一定相等。
周长相等的两个图形,面积不一定相等。
(2) 大单位换算小单位(乘它们之间的进率)
小单位换算大单位(除以它们之间的进率)
(3) 长度单位和面积单位的单位不同,无法比较。
(4)周长相等的两个长方形,面积不一定相等。面积相等的两个长方形,周长也不一定相等。
一、选择题
1.一个长方形的面积为6000平方分米,宽是4米,这个长方形的长是( )米。
A.150 B.15 C.25 D.250
2.学校操场面积为4000( ).
A.米 B.平方分米 C.平方米 D.平方厘米
3.边长1米的正方形,面积是( ),周长是( )。
A.1平方米;1米 B.1平方米;4米
C.4平方米;4米 D.4平方米;1米
4.以下( )的占地面积大约是45平方米.
A.1块黑板的面积 B.1间教室的占地面积
C.延庆区的占地面积 D.1个操场的占地面积
5.下图中每个小正方形的边长是1厘米,这个大正方形的面积是( )。
A.4厘米 B.16厘米 C.4平方厘来 D.16平方厘米
二、填空题
6.一个长方形周长24厘米,长与宽各增加5厘米,面积增加 平方厘米.
7.估计如图图形的面积大约各是多少平方厘米。(每个小方格表示1cm2)
约( )平方厘米 约( )平方厘米
8.在( )里填上“>”“<”或“=”.
2000平方分米( )1900平方米 3平方米( )30000平方厘米
500平方分米( )5平方米 4000平方米( )4000平方分米
70平方分米( )7平方米 500平方厘米( )60平方分米
9.填上适当的单位名称:上海市的面积大约是6340( )。
10.想一想,填一填。
(1)边长是( )分米的正方形,面积是1平方分米。
(2)边长是( )米的正方形,面积是1平方米。
(3)边长是( )厘米的正方形,面积是1平方厘米。
11.一块长方形的住宅用地,长12米,宽75米,这块住宅用地有 公顷.
12.大洋小学占地面积是9500( ).
13.边长分别是1米、1分米、1厘米的三个正方形中,面积最大的是边长为1 的正方形.
14.下图由小方格(每个小方格的面积是1平方厘米)围成的空白部分的周长是( )厘米,面积是( )平方厘米。
15.王大伯在自家的一面墙建一个鸡舍,想用12米长的竹篱笆围出最大的鸡舍,仔细想想,怎样建鸡舍的面积最大,面积是 平方米.
16.铅笔盒宽10( );数学课本长19( );课桌高7( );一个纽扣的面积大约是1( );一块橡皮的面积是8( );一支钢笔长13( );学校操场的面积是720( );一棵大树高12( );一张邮票的面积是4( ).
17.一个长方形花园的长是15米,宽是12米,这个花园的面积是 平方米。若把这个花园用篱笆围起来,至少需要 米长的篱笆。
三、判断题
18.1000平方厘米>20平方分米。( )
19.一个蓄水池深4.5米、长40米、宽30米,这个蓄水池的占地面积是1200平方米。( )
20.一个正方形边长是4分米,这个正方形的面积和周长相等. .(判断对错)
21.边长4米的正方形,它的周长和面积相等。( )
22.100公顷=1平方千米. .(判断对错)
四、解答题
23.长方形暖棚的长为22米,宽为14米,每平方米种6棵果苗.这个暖棚里一共可以种这样的果苗多少棵?
24.两块长方形花圃的长相等,第二块面积是多少?
25.一个长方形操场,长是82.4米,宽是41米.
26.涂色的正方形周长是60厘米(如图),求正方形的面积是多少?
27.一块正方形果园的四周围上了长68米的篱笆,这块正方形果园的面积是多少平方米?
28.一幅风景画长50厘米,宽40厘米,它的面积是多少平方厘米?
29.学校有一块长方形草地,如果把它的长缩短20米,这块草地就变成了边长是80米的正方形草地。原来这块长方形草地的面积是多少平方米?
先画图分析:
再列式解答:
30.用一根20米长的绳子,围一块长方形或正方形的绿地.小明用表格进行了探索.你发现了什么?
长(m ) 宽(m ) 面积(m )
9 1 9
8 2 16
7 3 21
6 4 24
5 5 25
我发现了:
31.长方形草坪的长是30米,面积是450平方米.扩建后宽没变,长增加到150米,面积会变成多少?
32.一块长方形苗圃的宽是7米,面积是238平方米,如果这个苗圃的长不变,宽增加到21米,扩大后的苗圃面积是多少平方米?
33.一个长方形,如果长和宽各增加8厘米,那么面积就增加384平方厘米.如果长和宽再各增加8厘米,那么面积又会增加多少平方厘米?
中小学教育资源及组卷应用平台 (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台 (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】平方分米和平方米之间的进率是100,据此将长方形的面积换算成平方米,再根据长方形的长=面积÷宽,把数据代入公式解答。
【详解】6000平方分米=60平方米
60÷4=15(米)
长是15米。
故答案为:B
【点睛】本题考查查长方形面积公式的灵活运用和面积单位的换算,关键是熟记公式。
2.C
【详解】略
3.B
【分析】根据正方形的面积公式,周长公式计算即可。
【详解】面积:1×1=1平方米;周长:1×4=4米。
故答案为:B
【点睛】熟悉正方形面积公式、周长公式是解答此题的关键。
4.B
【详解】略
5.D
【分析】观察上图可知,大正方形的边长为4厘米,4乘4即等于大正方形的面积,据此即可解答。
【详解】4×4=16(平方厘米)
故答案为:D
【点睛】明确大正方形的边长是多少是解答本题的关键。
6.85
【详解】试题分析:如图所示,增加的部分由①、②、③组成,设长方形的长为a,宽为b,则①的长为a,宽为5厘米,②的边长为5厘米,③的长为b,宽为5厘米,于是可以分别利用长方形和正方形的面积公式,表示出这三个图形的面积,再据“一个长方形周长24厘米”求出长和宽的和,即可求解.
解:设长方形的长为a,宽为b,
长和宽的和:a+b=24÷2=12(厘米),
增加部分的面积:
5a+5×5+5b,
=5(a+b)+25,
=5×12+25,
=60+25,
=85(平方厘米);
答:面积增加85平方厘米.
故答案为85.
点评:解答此题的关键是:弄清楚增加部分由哪些图形组成.
7. 8 12
【分析】左图可以看作一个长3厘米、宽2厘米的长方形的面积,再加上超出长方形面积范围的部分大约2格的面积;
右图可以看作一个长4厘米、宽3厘米的长方形的面积,据此解答。
【详解】左图:3×2+2
=6+2
=8(平方厘米)
右图:4×3=12(平方厘米)
(答案不唯一)
【点睛】解答此题,要注意认真分析图形,弄清图形所占的方格数是解答此题的关键。
8. < = = > < <
【详解】2000平方分米=20平方米 20平方米<1900平方米
3平方米=300平方分米=30000平方厘米
100平方分米=1平方米 500平方分米=5平方米
4000平方米=400000平方分米 400000平方分米 >4000平方分米
7平方米=700平方分米 70平方分米<7平方米
500平方厘米=5平方分米 5平方分米<60平方分米
9.平方千米
【分析】根据生活经验以及对面积单位和数据大小的认识,结合实际情况可知:计量上海市的面积用“平方千米”作单位。
【详解】上海市的面积大约是6340平方千米。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
10.(1)1
(2)1
(3)1
【详解】(1)边长是1分米的正方形,面积是1平方分米。生活中,经常能够接触到1平方分米大小的物品,如粉笔盒正面的面积大约是1平方分米,家里的肥皂盒大约是1平方分米那么大。
(2)边长是1米的正方形,面积是1平方米。教师的讲桌桌面大约是1平方米那么大。
(3)边长是1厘米的正方形,面积是1平方厘米。大拇指的指甲盖、骰子的每个面、电脑键盘上的按键等的大小都大约是1平方厘米。
11.0.09
【详解】试题分析:要求这块住宅用地的公顷数,就是求它的面积,利用面积=长×宽算出面积,再把平方米数换算成公顷数,用平方米数除以进率10000即可.
解:这块住宅用地的面积:12×75=900(平方米),
900平方米=0.09公顷.
答:这块住宅用地有0.09公顷.
故答案为0.09.
点评:此题考查长方形面积的计算方法和面积单位间的换算.
12.平方米
【解析】略
13.米
【详解】考虑长度,最长是的1米,所有边长为1米的正方形面积最大
【分析】联系实际
14. 20 21
【分析】根据“每个小方格的面积是1平方厘米”可知,每小格的边长是1厘米;所以空白部分的长是7厘米、宽是3厘米,再根据长方形面积=长×宽、长方形周长=(长+宽)×2,计算出长方形的面积和周长即可。
【详解】空白部分是一个长7厘米、宽3厘米的长方形,
(7+3)×2
=10×2
=20(厘米)
7×3=21(平方厘米)
所以,空白部分的周长是20厘米,面积是21平方厘米。
【点睛】确定空白部分的长与宽的长度是解题关键。
15.16
【详解】试题分析:由题意可知,围成一个正方形,则面积就最大,依据篱笆长度已知,即可求出正方形的边长,从而求出鸡舍的面积.
解:12÷3=4(米),
4×4=16(平方米);
答:将鸡舍围成一个正方形其面积最大,面积是16平方米.
故答案为16.
点评:解答此题的关键是明白:围成正方形面积最大,要注意篱笆只围三面.
16. 厘米 厘米 分米 平方厘米 平方厘米 厘米 平方米 米 平方厘米
【详解】区分长度单位和面积单位,常用的长度单位有米、分米、厘米,常用的面积单位有平方米、平方分米、平方厘米.
17. 180 54
【分析】长方形的面积=长×宽;长方形的周长=(长+宽)×2。
【详解】15×12=180(平方米);(15+12)×2=54(米)
故答案为:180;54。
18.×
【分析】平方厘米和平方分米之间的进率是100,据此解答即可。
【详解】1000平方厘米=10平方分米
10平方分米<20平方分米
1000平方厘米<20平方分米
故答案为:×
【点睛】本题考查面积单位的换算。把低级单位换算成高级单位,就除以单位间的进率;把高级单位换算成低级单位,就乘单位间的进率。
19.√
【分析】根据长方形的面积=长×宽,把数据代入公式求出这个水池的占地面积与1200平方米进行比较,如果占地面积等于1200平方米,此说法是正确的,否则是错误的。据此判断。
【详解】40×30=1200(平方米)
故题干说法正确。
故答案为:√
【点睛】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
20.×
【详解】试题分析:根据正方形的周长、面积的意义,正方形的周长是指围成这个正方形的4条边的长度和;正方形的面积是指围成平面的大小;因为周长和面积不是同类量所以不能进行比较.据此判断.
解答:解:正方形的周长是指围成这个正方形的4条边的长度和;正方形的面积是指围成平面的大小;
因为周长和面积不是同类量所以不能进行比较.
所以一个正方形边长是4分米,这个正方形的面积和周长相等.这种说法是错误的.
故答案为×.
点评:此题考查的目的是理解掌握周长、面积的意义,明确:只有同类量才能比较大小.
21.×
【分析】
封闭图形一周的长度,是它的周长;物体的表面或围成的平面图形的大小,叫面积。根据周长、面积的意义可知,因为周长和面积是不同的两个量,所以无法比较。
【详解】
正方形的周长是指围成正方形四条边的总长度,正方形的面积是指围成正方形的大小,意义不同;
正方形的周长是边长×4,正方形的面积是边长×边长,计算方法不同;
周长的计量单位是长度单位,面积的计量单位是面积单位,计量单位不同;
故无法比较,所以原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握周长、面积的意义及应用。周长和面积是不同的两个量,无法比较大小。
22.√
【详解】试题分析:根据面积单位公顷与平方千米之间的关系,1平方千米=100公顷.
解答:解:100公顷=1平方千米.
故答案为√.
点评:本题是考查面积单位平方千米与公顷之间的进率,属于基础知识,要记住.
23.1848棵
【详解】试题分析:先利用长方形的面积公式求出暖棚的面积,再乘每平方米种的果苗的棵数,即可得解.
解:22×14×6,
=308×6,
=1848(棵),
答:这个暖棚里一共可以种这样的果苗1848棵.
点评:此题主要考查长方形的面积的计算方法在实际生活中的应用.
24.744平方米
【分析】根据长方形的面积公式S=ab,得出a=S÷b,求出第一块长方形花圃的长,即第二块长方形花圃的长,再利用长方形的面积公式求出第二块花圃的面积.
【详解】248÷7×21
=×21
=744(平方米)
答:第二块的面积是744平方米.
25.3378.4
【详解】试题分析:根据长方形的面积公式:s=ab,把数据代入公式解答即可.
解:82.4×41=3378.4(平方米),
答:这个操场的面积是3378.4平方米.
点评:此题主要考查长方形的面积公式的灵活运用.
26.225平方米
【分析】根据正方形周长公式用周长除以4即可求出正方形的边长,用边长乘边长即可求出正方形的面积。
【详解】(60÷4)×(60÷4)
=15×15
=225(平方米)
答:正方形的面积是225平方米。
【点睛】本题主要考查学生对正方形的周长和面积公式的掌握及灵活运用。
27.果园的面积是289平方米
【详解】试题分析:先根据正方形的周长公式求出这个正方形果园的边长,再利用正方形的面积=边长×边长计算即可解答.
解:68÷4=17(米),
17×17=289(平方米),
答:果园的面积是289平方米.
点评:此题考查正方形的周长与面积公式的计算应用,熟记公式即可解答.
28.2000平方厘米.
【详解】试题分析:长方形的面积=长×宽,长和宽已知,代入公式即可求解.
解:50×40=2000(平方厘米);
答:这幅风景画的面积是2000平方厘米.
【点评】此题主要考查长方形的面积的计算方法.
29.;8000平方米。
【分析】先画出图形,因为长缩短20米以后是边长为80米的正方形,那么原来长方形的长就为100米,宽为80米,再根据长方形面积=长×宽,求出原来长方形草地面积即可。
【详解】
(80+20)×80
=100×80
=8000(平方米)
答:原来这块长方形草地的面积是8000平方米
【点睛】本题考查的是长方形的面积,关键是要将原来长方形的长求出来。
30.我发现了:长方形的周长相同时,长与宽越接近,长方形的面积越大。
【详解】略
31.2250平方米
【详解】试题分析:先根据长方形草坪原来的面积求出草坪的宽是450÷30=15(米),再利用长方形的面积=长×宽即可求出扩建后的面积.
解:450÷30×150,
=15×150,
=2250(平方米),
答:面积是2250平方米.
点评:此题考查长方形的面积公式的计算应用,关键是明确草坪的宽.
32.714平方米
【详解】试题分析:根据题意,可依据原来长方形面积除以宽计算出长方形的长,宽增加到21米,即宽为21米,根据长方形的面积公式进行计算即可得到答案.
解:长方形的长:238÷7=34(米),
扩大后的面积为:34×21=714(平方米);
答:扩大后的苗圃面积是714平方米.
点评:解答此题的关键是根据原来的长方形的面积计算出长方形的长,然后再依据长方形的面积公式进行计算即可.
33.512平方厘米
【详解】试题分析:如图:增加部分是面积是384平方厘米,先用“384﹣8×8=320平方厘米”求出增加的两个长方形的面积的和,因为这两个长方形都有一条边是8,所以原来长宽的和为:320÷8=40厘米;第二次增加后的长宽和为:40+8×2=56厘米,增加的面积:56×8+8×8=512平方厘米;进而得出结论.
解:如图:[(384﹣8×8)÷8+8×2]×8+8×8,
=[40+16]×8+64,
=512(平方厘米);
答:面积又会增加512平方厘米.
点评:此题较难,解答此题的关键:求出长方形的长和宽的和,进而找出长方形的长和宽的和、增加的长和宽的长度和增加的面积三者之间的关系,是解答此题的关键所在.
答案第1页,共2页
答案第1页,共2页
同课章节目录
