【期末提升讲义】专题三:长方体和正方体--2024-2025学年五年级下册数学讲练测人教版
文档属性
| 名称 | 【期末提升讲义】专题三:长方体和正方体--2024-2025学年五年级下册数学讲练测人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 581.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
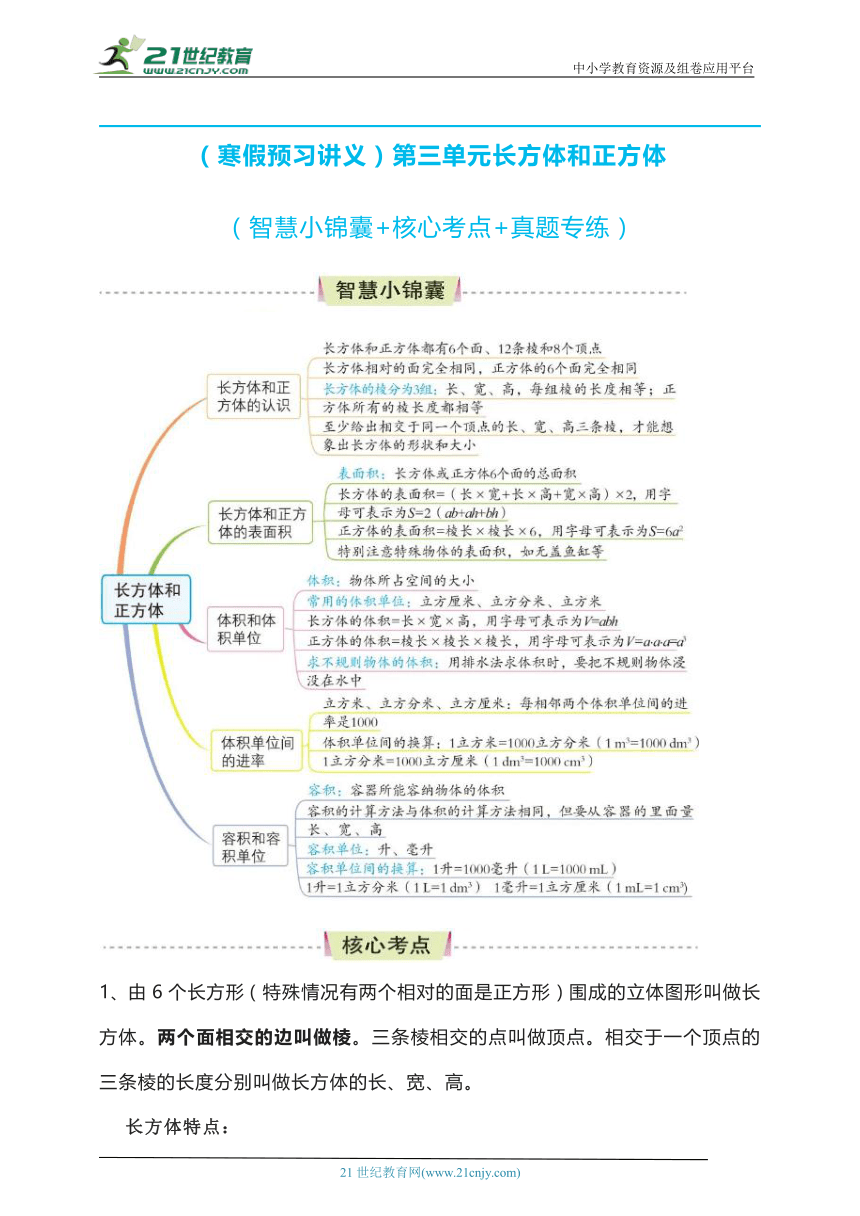
(寒假预习讲义)第三单元长方体和正方体
(智慧小锦囊+核心考点+真题专练)
1、由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。两个面相交的边叫做棱。三条棱相交的点叫做顶点。相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
长方体特点:
(1)有6个面,8个顶点,12条棱,相对的面的面积相等,相对的棱的长度相等。
(2)一个长方体最多有6个面是长方形,最少有4个面是长方形,最多有2个面是正方形。
2、由6个完全相同的正方形围成的立体图形叫做正方体(也叫做立方体)。
正方体特点:
(1)正方体有12条棱,它们的长度都相等。
(2)正方体有6个面,每个面都是正方形,每个面的面积都相等。
(3)正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
相同点 不同点
面 棱
长方体 都有6个面,12条棱,8个顶点。 6个面都是长方形。 (有可能有两个相对的面是正方形)。 相对的棱的长度都相等
正方体 6个面都是正方形。 12条棱都相等。
3、长方体、正方体有关棱长计算公式:
长方体的棱长总和=(长+宽+高)×4=长×4+宽×4+高×4
L=(a+b+h)×4
长=棱长总和÷4-宽 -高
a=L÷4-b-h
宽=棱长总和÷4-长 -高
b=L÷4-a-h
高=棱长总和÷4-长 -宽
h=L÷4-a-b
正方体的棱长总和=棱长×12
L=a×12
正方体的棱长=棱长总和÷12
a=L÷12
4、长方体或正方体6个面和总面积叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
无底(或无盖)
长方体表面积= 长×宽+(长×高+宽×高)×2
S=2(ab+ah+bh)-ab
S=2(ah+bh)+ab
无底又无盖长方体表面积=(长×高+宽×高)×2
S=2(ah+bh)
贴墙纸
正方体的表面积=棱长×棱长×6 S=a×a×6 用字母表示:S= 6a2
生活实际:
油箱、罐头盒等都是6个面
游泳池、鱼缸等都只有5个面
水管、烟囱等都只有4个面。
注意1:用刀分开物体时,每分一次增加两个面。(表面积相应增加)
注意2:长方体或正方体的长、宽、高同时扩大几倍,表面积会扩大倍数的平方倍。
(如长、宽、高各扩大2倍,表面积就会扩大到原来的4倍)。
5、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V÷b÷h
宽=体积÷长÷高 b=V÷a÷h
高=体积÷长÷宽 h= V÷a÷b
正方体的体积=棱长×棱长×棱长
V=a×a×a =a3
读作“a的立方”表示3个a相乘,(即a·a·a)
长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高
用字母表示:V=S h(横截面积相当于底面积,长相当于高)。
注意:一个长方体和一个正方体的棱长总和相等,但体积不一定相等。
6、箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
固体一般就用体积单位,计量液体的体积,如水、油等。
常用的容积单位有升和毫升也可以写成L和ml。
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
(1L=1dm3 1ml=1cm3)
长方体或正方体容器容积的计算方法,跟体积的计算方法相同。
但要从容器里面量长、宽、高。(所以,对于同一个物体,体积大于容积。)
注意:长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。
(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:
V物体 =V现在-V原来
也可以 V物体 =S×(h现在- h原来)
V物体 =S×h升高
8、【体积单位换算】
大单位×进率=小单位
小单位÷进率=大单位
进率:1立方米=1000立方分米=1000000立方厘米(立方相邻单位进率1000)
1立方分米=1000立方厘米=1升=1000毫升
1立方厘米=1毫升
1平方米=100平方分米=10000平方厘米
1平方千米=100公顷=1000000平方米
注意:长方体与正方体关系
把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。
重量单位进率,时间单位进率,长度单位进率
大单位×进率=小单位
小单位÷进率=大单位
长度单位:
1千米 =1000 米 1 分米=10 厘米
1厘米=10毫米 1分米=100毫米
1米=10分米=100厘米=1000毫米
(相邻单位进率10)
面积单位:
1平方千米=100公顷
1平方米=100平方分米
1平方分米=100平方厘米
1公顷=10000平方米(平方相邻单位进率100)
质量单位:
1吨=1000千克
1千克=1000克
人民币:
1元=10角 1角=10分 1元=100分
一、选择题
1.一个长方体的高不变,长和宽分别扩大到原来的3倍,那么它的体积扩大到原来的( )。
A.6倍 B.9倍 C.27倍 D.12倍
2.把1.2升糖水装入容积是100毫升的瓶子里,能装满( )瓶。
A.10 B.12 C.120 D.1200
3.妈妈买了一瓶饮料,净含量为560mL。这里的“560mL”指的是( )。
A.饮料瓶的体积 B.饮料的体积 C.饮料瓶的容积
4.小华把棱长是1cm的小正方体积木靠墙角搭成了一个立体图形(如图),露在外面的面积是( )cm2。
A.20 B.21 C.24
5.下面的平面图中,( )不能折成正方体。
A. B. C.
6.一个长方体长5cm,宽4cm,高3cm。它的体积是( )cm3。
A.60 B.94 C.20
二、填空题
7.一个长方体的底面是正方形,它的表面积是84平方厘米。若这个长方体恰好能裁成三个体积相等的正方体,这样表面积增加了( )平方厘米。
8.一根长52厘米的铁丝,可以焊接成一个长6厘米,宽3厘米,高( )厘米的长方体。
9.把84L水倒入一个从里面量长为7dm、宽为4dm、高为5dm的长方体水池内,池内水的高度是( )dm。
10.一个长12cm、宽10cm、高8cm的长方体,切割成2个完全相同的长方体,表面积最大可增加( )cm2。
11.计量容积,一般就用( )。计量液体的体积,如水、油等,常用容积单位( )和( ),也可以写成( )和( )。
12.一个长5dm、宽3dm、高5dm的长方体玻璃缸内盛有2dm深的水,放入一个石块后,水深2.2dm,这个石块的体积是( )dm3。
13.挖一个长和宽都是5m的长方体菜窖,要使菜窖的容积是40m3,应该挖( )m深。
14.一个长方体的底面是一个边长为4分米的正方形,高3.5厘米,则长方体前、后、左、右四个面的面积之和是( )。
15.至少需要( )cm长的铁丝,才能做一个底面周长是10cm,高是5cm的长方体框架。
16.用棱长是1dm的小正方体摆成一个稍大的正方体,至少需要( )个这样的小正方体。
17.如图,正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是( )cm2。
18.在下图长方体的各个顶点间连线,使得从每个顶点出发所连的线段均大于线段,则“从A点出发可以连( )条大于的线段,这个长方体中一共可以连( )条大于的线段”。
三、判断题
19.有6个面、12条棱、8个顶点的物体不是长方体就是正方体。( )
20.李师傅家的冰箱容积有220毫升。( )
21.在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与其它3个数据不相等。( )
22.把一块体积为50立方厘米球形橡皮泥捏成一个正方体,那么这个正方体的体积也等于50立方厘米。( )
23.蜡像厂把一个实心工艺品“千里马”熔化后,又在无损耗的情况下塑成了另一个实心工艺品“拓荒牛”,这两件工艺品中,“千里马”的体积等于“拓荒牛”的体积。( )
四、计算题
24.求下列组合图形的体积。(单位:cm)
五、解答题
25.用两个相同的正方体木块拼成一个长方体,棱长总和减少了32厘米,原来每个正方体木块的棱长是多少?
26.玉山家具厂订购500根方木,每根方木横截面的面积是2.4dm2,长是3m。这些木料一共是多少方?
27.一个高为4.5分米的长方体容器,水深3分米时装了27升水,如果把它装满,能装多少升水?
28.在一个长8米、宽5米、高2米的水池中注满水,然后把一条长3米、宽2米、高5米的石柱立着放入池中,水池溢出的水的体积是多少?
29.王师傅用铁丝制作一个孔明灯框架,它的底面是正方形且周长是80厘米,高是25厘米,要把它的表面糊上彩色纸(底面不糊纸)。王师傅至少要买多少平方分米的彩色纸?
30.林伯伯家准备砌一道长15米、厚3分米、高2米的砖墙,如果每立方米用砖530块,林伯伯至少要准备多少块砖?
31.红星小学要建一个长80米、宽60米的长方形足球场,先要铺5厘米厚的煤渣,然后铺12厘米厚的三合土。需要煤渣、三合土各多少立方米?
32.把一个长、宽、高分别是8分米、6分米、3分米的长方体锯成一个最大的正方体。这个正方体的体积是多少立方分米?剩下部分的体积是多少立方分米?
《第三单元长方体和正方体(单元测试)--2024-2025学年五年级下册数学常考易错题人教版》参考答案
1.B
【分析】假设长方体的长3厘米,宽2厘米,高4厘米,根据长方体体积=长×宽×高,分别计算出长和宽扩大前后的体积,扩大后的体积÷原来的体积=扩大到原来的倍数。
【详解】假设长方体的长3厘米,宽2厘米,高4厘米。
3×2×4=24(立方厘米)
(3×3)×(2×3)×4
=9×6×4
=216(立方厘米)
216÷24=9
它的体积扩大到原来的9倍。
故答案为:B
2.B
【分析】1升=1000毫升,用乘法把高级单位转化为低级单位,装满的瓶数=糖水的总毫升数÷瓶子的容积,据此解答。
【详解】1.2×1000=1200(毫升)
1200÷100=12(瓶)
所以,能装满12瓶。
故答案为:B
3.B
【分析】物体所占空间的大小叫做它的体积;容积指箱子,油桶,仓库等所能容纳物体的体积。
【详解】题目中的“净含量”是指饮料瓶内实际装有的饮料量,即饮料本身的体积;
A.(饮料瓶的体积)是指瓶子本身占据的空间大小,与内部装的饮料量无关;
B.(饮料的体积)正确,因为“560mL”直接表示瓶中饮料的实际体积,符合“净含量”的定义;
C.(饮料瓶的容积)是指瓶子最多能容纳的液体体积,可能大于净含量(例如瓶子设计为600mL,但实际装560mL饮料)。
故答案为:B
4.B
【分析】每个小正方形的面积是1cm2,分别计算出立体图形的前、右、上三个面各有多少个小正方形,求出三者之和,即可知道露出的面积是多少。
【详解】1×1=1(cm2)
前面露出6个小正方形,右面露出6个小正方形,上面露出9个小正方形。
6+6+9=21(个)
21×1=21(cm2)
露在外面的面积是21cm2。
故答案为:B
5.A
【分析】11种正方体展开图:“141”型、“231”型、“222”型、“33”型 :
据此逐项判断即可。
【详解】根据分析可得:
A.不能折成正方体。
B.是正方体展开图 “141”型,能折成正方体。
C.是正方体展开图 “141”型,能折成正方体。
故答案为:A
6.A
【分析】长方体的体积=长×宽×高,把题目中这个长方体的长、宽、高代入公式计算,据此解答。
【详解】5×4×3
=20×3
=60(cm3)
所以,它的体积是60cm3。
故答案为:A
7.24
【分析】根据题意作图如下:
从图中可知:这个长方体恰好能裁成三个体积相等的正方体,底面是正方形,前后左右面就等于3×4=12(个)正方形面的大小,这个长方体表面积(84平方厘米)就相当于12+2=14(个)正方形面的大小。裁成三个相等的正方体,表面积就增加了4个正方形的面。用这个长方体的表面积÷14即可得一个正方形的面积,再乘4即可求出增加了的表面积。
【详解】84÷14×4=24(平方厘米)
这样表面积增加了24平方厘米。
8.4
【分析】根据题意,用一根铁丝焊接成一个长方体,则这根铁丝的长度就是长方体的棱长总和;根据长方体的棱长总和=(长+宽+高)×4,可知长方体的高=棱长总和÷4-长-宽,代入数据计算即可。
【详解】52÷4-6-3
=13-6-3
=4(厘米)
高是4厘米。
9.3
【分析】根据:长方体的体积=长×宽×高,池内水的高=容积÷(长×宽),据此计算。
【详解】84L=84dm3
84÷(7×4)
=84÷28
=3(dm)
所以池内水的高度是3dm。
10.240
【分析】要满足表面积增加的最大,沿原来长方体的最大面平行切开,表面积增加两个切面的面积,长方形的面积=长×宽,据此代入数据计算即可解答。
【详解】12×10×2
=120×2
=240(cm2)
表面积最大可增加240cm2。
11. 体积单位 升 毫升 L mL
【详解】容器所能容纳物体的体积,通常叫作它的容积。计量容积,一般就用体积单位。计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写成L和mL,1L=1000mL,容积单位和体积单位的关系:1L=1dm3,1mL=1cm3。
12.3
【分析】水面上升的体积就是这个石块的体积,长方体玻璃缸的长×宽×水面上升的高度=石块体积,据此列式计算。
【详解】5×3×(2.2-2)
=15×0.2
=3(dm3)
这个石块的体积是3dm3。
13.1.6
【分析】菜窖的深相当于长方体的高,根据长方体的高=容积÷长÷宽,列式计算即可。
【详解】高:40÷5÷5
=8÷5
=1.6(m)
所以应该挖1.6m深。
14.560平方厘米/560cm2/5.6平方分米/5.6dm2
【分析】根据正方形和长方形的特征可知,长方体前、后、左、右四个面相同,已知长和宽都是4分米,高是3.5厘米,先统一单位,然后根据长方形的面积公式,先求出1个面的面积再乘4即可求出前、后、左、右4个面的面积和。
【详解】4分米=40厘米
40×3.5×4
=140×4
=560(平方厘米)
长方体前、后、左、右四个面的面积之和是560平方厘米。
15.40
【分析】求需要铁丝的长度,就是求这个长方体棱长总和;已知一个底面周长是10cm,一个底面周长是2个长、2个宽的和,一个长方体有4条长,4条宽、4条高,用一个底面周长×2,求出4条长与4条宽的长度和,再用高×4,求出4条高的和,再把它们相加,即可解答。
【详解】10×2+5×4
=20+20
=40(cm)
至少需要40cm长的铁丝,才能做一个底面周长是10cm,高是5cm的长方体框架。
16.8
【分析】根据正方体的特征,12条棱都相等;那么拼成的大正方体的棱长最少由2个同样的小正方体的棱长组成,根据正方体体积:V=a3可以求出至少需要同样的小正方体的个数。
【详解】如图:
2×2×2
=4×2
=8(dm3)
8÷(1×1×1)
=8÷(1×1)
=8÷1
=8(个)
用棱长是1dm的小正方体摆成一个稍大的正方体,至少需要8个这样的小正方体。
17.96
【分析】分析题目,剩下物体的表面积等于棱长是4cm的正方体的表面积,据此结合正方体的表面积=棱长×棱长×6列式计算即可。
【详解】4×4×6
=16×6
=96(cm2)
正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是96cm2。
18. 3 12
【分析】从A点出发的对角线有AC、AF、AG、AH,其中AH 小于线段AB;
长方体有8个顶点,从每个顶点出发的情况是一样的。 从一个顶点出发可以连3条大于AB的线段,若直接用8×3=24来计算,会出现每条线段都被重复计算了2次的情况(因为一条线段有两个端点)。 所以长方体中大于AB的线段总数为8×3÷2=12条。
【详解】从A点出发的对角线有AC、AF、AG都大于AB;
前后面的对角线(4条),上下面的对角线(4条),AG、BH、EC、DF,一共有12条。
8×3÷2=12(条)
则“从A点出发可以连3条大于的线段,这个长方体中一共可以连12条大于的线段”。
19.×
【分析】根据上面的分析,棱台也有6个面、12条棱、8个顶点,棱台既不是长方体也不是正方体。据此分析判断。
【详解】据分析可知,有6个面、12条棱、8个顶点的物体不一定是长方体或正方体。原题说法错误。
故答案为:×
20.×
【分析】常见的容积单位有毫升、升,计量比较少的液体,通常用毫升作单位,1瓶可乐的容积差不多是300毫升,1升相当于2瓶矿泉水的容积。据此判断。
【详解】结合生活实际,冰箱容积一般用升作单位,所以原题说法错误。
故答案为:×
21.×
【分析】根据1 m3=1000 dm3,1 dm3=1000 cm3,高级单位换算成低级单位,乘进率,低级单位换算成高级单位,除以进率。先将所有数据都换算成以dm3为单位,再比较即可判断。
【详解】因为:4.06m3=4060 dm3
406000cm3=406 dm3
4060000cm3=4060 dm3
所以:4.06m3=4060 dm3=4060000cm3
4.06m3≠406000 dm3
在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与4060dm3、4060000cm3相等,4.06m3与406000cm3不相等。因此原题说法不正确。
故答案为:×
22.√
【分析】体积表示物体所占空间的大小,不管怎么捏,橡皮泥是不会变少的,也就是说它的体积不会变小,于是捏成正方体后,体积依旧是原来的50立方厘米。
【详解】球形橡皮泥捏成一个正方体,形状虽然发生了变化,但它所占空间的大小一样,也就是体积没有发生变化,仍就是50立方厘米。原题干说法正确。
故答案为:√
【点睛】本题考查了体积的等积变形,明确同一个物体,形状无论怎么变化,体积始终保持不变。
23.√
【分析】根据体积的意义:物体所占空间的大小是物体的体积;把“千里马”熔化塑成了“拓荒牛”,可知只是两件工艺品的形状的变化,而体积没有变化。据此解答。
【详解】由分析可知:
蜡像厂把一个实心工艺品“千里马”熔化后,又在无损耗的情况下塑成了另一个实心工艺品“拓荒牛”,这两件工艺品中,“千里马”的体积等于“拓荒牛”的体积。原说法正确。
故答案为:√
24.27cm3;232cm3
【分析】左边:组合图形的体积=两个长方体体积之和,根据长方体的体积=长×宽×高,代入数据解答即可;
右边:组合图形的体积=长方体的体积-正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据解答即可。
【详解】5×3×1+2×2×3
=15+4×3
=15+12
=27(cm3)
8×6×5-2×2×2
=48×5-4×2
=240-8
=232(cm3)
左边组合图形的体积为27cm3,右边组合图形的体积为232cm3。
25.4厘米
【分析】两个相同的正方体木块拼成一个长方体,减少了8条棱长和,用32÷8,即可求出原来每个正方体木块的棱长。
【详解】32÷8=4(厘米)
答:原来每个正方体木块的棱长是4厘米。
26.36方
【分析】每根木料的体积=横截面积×长,木料总体积=每根的体积×500,据此计算。
【详解】2.4dm2=0.024m2
0.024×3×500
=0.072×500
=36(方)
答:这些木料一共是36方。
27.40.5升
【分析】根据1升=1立方分米,所以27升等于27立方分米,又知当水深3分米时,容器装了27升水,根据长方体的体积V=Sh,所以S=V÷h,再用长方体容器的底面积乘长方体容器的高,即可求出长方体容器能装满多少升的水。
【详解】27升=27立方分米
27÷3=9(平方分米)
9×4.5=40.5(立方分米)
40.5立方分米=40.5升
答:能装40.5升水。
28.12立方米
【分析】由于是石柱立着放入池中,放入水中的石柱高度是2米,根据,求出放入水中石柱的体积,放入水中石柱的体积就是溢出的水的体积,据此即可解答。
【详解】3×2×2=12(立方米)
答:水池溢出的水的体积是12立方米。
29.24平方分米
【分析】已知底面的周长是80厘米,底面是正方形,根据正方形的边长=周长÷4,因此边长为:80÷4=20厘米。这个长方体的框架,前后左右面4个面是形状大小相等的长方形,因此彩色纸的面积=前后左右面+上面=边长×高×4+边长×边长,据此代入数据计算,即可求出彩色纸的面积。再根据1平方分米=100平方厘米,将结果换算成平方分米。
【详解】80÷4=20(厘米)
20×25×4+20×20
=2000+400
=2400(平方厘米)
2400平方厘米=24平方分米
答:王师傅至少要买24平方分米的彩色纸。
30.4770块
【分析】根据1米=10分米,统一单位,砖墙的厚相当于长方体的宽,根据长方体体积=长×宽×高,求出砖墙的体积,砖墙的体积×每立方米用砖块数=砖的总块数,据此列式解答。
【详解】3分米=0.3米
15×0.3×2×530
=9×530
=4770(块)
答:林伯伯至少要准备4770块砖。
31.240立方米;576立方米
【分析】根据1米=100厘米,统一单位,煤渣和三合土的厚相当于长方体的高,根据长方体体积=长×宽×高,分别计算出煤渣、三合土的体积即可。
【详解】5厘米=0.05米、12厘米=0.12米
80×60×0.05=240(立方米)
80×60×0.12=576(立方米)
答:需要煤渣240立方米、三合土576立方米。
32.27立方分米;117立方分米
【分析】由题意可知,锯成的这个最大的正方体的棱长等于长方体的高,再根据长方体的体积=长×宽×高、正方体的体积=棱长×棱长×棱长分别求出长方体和正方体的体积,最后用长方体的体积减去锯成的正方体体积就是剩下部分的体积,据此解答即可。
【详解】3×3×3
=9×3
=27(立方分米)
8×6×3
=48×3
=144(立方分米)
144-27=117(立方分米)
答:这个正方体的体积是27立方分米,剩下部分的体积是117立方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(寒假预习讲义)第三单元长方体和正方体
(智慧小锦囊+核心考点+真题专练)
1、由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。两个面相交的边叫做棱。三条棱相交的点叫做顶点。相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
长方体特点:
(1)有6个面,8个顶点,12条棱,相对的面的面积相等,相对的棱的长度相等。
(2)一个长方体最多有6个面是长方形,最少有4个面是长方形,最多有2个面是正方形。
2、由6个完全相同的正方形围成的立体图形叫做正方体(也叫做立方体)。
正方体特点:
(1)正方体有12条棱,它们的长度都相等。
(2)正方体有6个面,每个面都是正方形,每个面的面积都相等。
(3)正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
相同点 不同点
面 棱
长方体 都有6个面,12条棱,8个顶点。 6个面都是长方形。 (有可能有两个相对的面是正方形)。 相对的棱的长度都相等
正方体 6个面都是正方形。 12条棱都相等。
3、长方体、正方体有关棱长计算公式:
长方体的棱长总和=(长+宽+高)×4=长×4+宽×4+高×4
L=(a+b+h)×4
长=棱长总和÷4-宽 -高
a=L÷4-b-h
宽=棱长总和÷4-长 -高
b=L÷4-a-h
高=棱长总和÷4-长 -宽
h=L÷4-a-b
正方体的棱长总和=棱长×12
L=a×12
正方体的棱长=棱长总和÷12
a=L÷12
4、长方体或正方体6个面和总面积叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
无底(或无盖)
长方体表面积= 长×宽+(长×高+宽×高)×2
S=2(ab+ah+bh)-ab
S=2(ah+bh)+ab
无底又无盖长方体表面积=(长×高+宽×高)×2
S=2(ah+bh)
贴墙纸
正方体的表面积=棱长×棱长×6 S=a×a×6 用字母表示:S= 6a2
生活实际:
油箱、罐头盒等都是6个面
游泳池、鱼缸等都只有5个面
水管、烟囱等都只有4个面。
注意1:用刀分开物体时,每分一次增加两个面。(表面积相应增加)
注意2:长方体或正方体的长、宽、高同时扩大几倍,表面积会扩大倍数的平方倍。
(如长、宽、高各扩大2倍,表面积就会扩大到原来的4倍)。
5、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V÷b÷h
宽=体积÷长÷高 b=V÷a÷h
高=体积÷长÷宽 h= V÷a÷b
正方体的体积=棱长×棱长×棱长
V=a×a×a =a3
读作“a的立方”表示3个a相乘,(即a·a·a)
长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高
用字母表示:V=S h(横截面积相当于底面积,长相当于高)。
注意:一个长方体和一个正方体的棱长总和相等,但体积不一定相等。
6、箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
固体一般就用体积单位,计量液体的体积,如水、油等。
常用的容积单位有升和毫升也可以写成L和ml。
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
(1L=1dm3 1ml=1cm3)
长方体或正方体容器容积的计算方法,跟体积的计算方法相同。
但要从容器里面量长、宽、高。(所以,对于同一个物体,体积大于容积。)
注意:长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。
(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:
V物体 =V现在-V原来
也可以 V物体 =S×(h现在- h原来)
V物体 =S×h升高
8、【体积单位换算】
大单位×进率=小单位
小单位÷进率=大单位
进率:1立方米=1000立方分米=1000000立方厘米(立方相邻单位进率1000)
1立方分米=1000立方厘米=1升=1000毫升
1立方厘米=1毫升
1平方米=100平方分米=10000平方厘米
1平方千米=100公顷=1000000平方米
注意:长方体与正方体关系
把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。
重量单位进率,时间单位进率,长度单位进率
大单位×进率=小单位
小单位÷进率=大单位
长度单位:
1千米 =1000 米 1 分米=10 厘米
1厘米=10毫米 1分米=100毫米
1米=10分米=100厘米=1000毫米
(相邻单位进率10)
面积单位:
1平方千米=100公顷
1平方米=100平方分米
1平方分米=100平方厘米
1公顷=10000平方米(平方相邻单位进率100)
质量单位:
1吨=1000千克
1千克=1000克
人民币:
1元=10角 1角=10分 1元=100分
一、选择题
1.一个长方体的高不变,长和宽分别扩大到原来的3倍,那么它的体积扩大到原来的( )。
A.6倍 B.9倍 C.27倍 D.12倍
2.把1.2升糖水装入容积是100毫升的瓶子里,能装满( )瓶。
A.10 B.12 C.120 D.1200
3.妈妈买了一瓶饮料,净含量为560mL。这里的“560mL”指的是( )。
A.饮料瓶的体积 B.饮料的体积 C.饮料瓶的容积
4.小华把棱长是1cm的小正方体积木靠墙角搭成了一个立体图形(如图),露在外面的面积是( )cm2。
A.20 B.21 C.24
5.下面的平面图中,( )不能折成正方体。
A. B. C.
6.一个长方体长5cm,宽4cm,高3cm。它的体积是( )cm3。
A.60 B.94 C.20
二、填空题
7.一个长方体的底面是正方形,它的表面积是84平方厘米。若这个长方体恰好能裁成三个体积相等的正方体,这样表面积增加了( )平方厘米。
8.一根长52厘米的铁丝,可以焊接成一个长6厘米,宽3厘米,高( )厘米的长方体。
9.把84L水倒入一个从里面量长为7dm、宽为4dm、高为5dm的长方体水池内,池内水的高度是( )dm。
10.一个长12cm、宽10cm、高8cm的长方体,切割成2个完全相同的长方体,表面积最大可增加( )cm2。
11.计量容积,一般就用( )。计量液体的体积,如水、油等,常用容积单位( )和( ),也可以写成( )和( )。
12.一个长5dm、宽3dm、高5dm的长方体玻璃缸内盛有2dm深的水,放入一个石块后,水深2.2dm,这个石块的体积是( )dm3。
13.挖一个长和宽都是5m的长方体菜窖,要使菜窖的容积是40m3,应该挖( )m深。
14.一个长方体的底面是一个边长为4分米的正方形,高3.5厘米,则长方体前、后、左、右四个面的面积之和是( )。
15.至少需要( )cm长的铁丝,才能做一个底面周长是10cm,高是5cm的长方体框架。
16.用棱长是1dm的小正方体摆成一个稍大的正方体,至少需要( )个这样的小正方体。
17.如图,正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是( )cm2。
18.在下图长方体的各个顶点间连线,使得从每个顶点出发所连的线段均大于线段,则“从A点出发可以连( )条大于的线段,这个长方体中一共可以连( )条大于的线段”。
三、判断题
19.有6个面、12条棱、8个顶点的物体不是长方体就是正方体。( )
20.李师傅家的冰箱容积有220毫升。( )
21.在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与其它3个数据不相等。( )
22.把一块体积为50立方厘米球形橡皮泥捏成一个正方体,那么这个正方体的体积也等于50立方厘米。( )
23.蜡像厂把一个实心工艺品“千里马”熔化后,又在无损耗的情况下塑成了另一个实心工艺品“拓荒牛”,这两件工艺品中,“千里马”的体积等于“拓荒牛”的体积。( )
四、计算题
24.求下列组合图形的体积。(单位:cm)
五、解答题
25.用两个相同的正方体木块拼成一个长方体,棱长总和减少了32厘米,原来每个正方体木块的棱长是多少?
26.玉山家具厂订购500根方木,每根方木横截面的面积是2.4dm2,长是3m。这些木料一共是多少方?
27.一个高为4.5分米的长方体容器,水深3分米时装了27升水,如果把它装满,能装多少升水?
28.在一个长8米、宽5米、高2米的水池中注满水,然后把一条长3米、宽2米、高5米的石柱立着放入池中,水池溢出的水的体积是多少?
29.王师傅用铁丝制作一个孔明灯框架,它的底面是正方形且周长是80厘米,高是25厘米,要把它的表面糊上彩色纸(底面不糊纸)。王师傅至少要买多少平方分米的彩色纸?
30.林伯伯家准备砌一道长15米、厚3分米、高2米的砖墙,如果每立方米用砖530块,林伯伯至少要准备多少块砖?
31.红星小学要建一个长80米、宽60米的长方形足球场,先要铺5厘米厚的煤渣,然后铺12厘米厚的三合土。需要煤渣、三合土各多少立方米?
32.把一个长、宽、高分别是8分米、6分米、3分米的长方体锯成一个最大的正方体。这个正方体的体积是多少立方分米?剩下部分的体积是多少立方分米?
《第三单元长方体和正方体(单元测试)--2024-2025学年五年级下册数学常考易错题人教版》参考答案
1.B
【分析】假设长方体的长3厘米,宽2厘米,高4厘米,根据长方体体积=长×宽×高,分别计算出长和宽扩大前后的体积,扩大后的体积÷原来的体积=扩大到原来的倍数。
【详解】假设长方体的长3厘米,宽2厘米,高4厘米。
3×2×4=24(立方厘米)
(3×3)×(2×3)×4
=9×6×4
=216(立方厘米)
216÷24=9
它的体积扩大到原来的9倍。
故答案为:B
2.B
【分析】1升=1000毫升,用乘法把高级单位转化为低级单位,装满的瓶数=糖水的总毫升数÷瓶子的容积,据此解答。
【详解】1.2×1000=1200(毫升)
1200÷100=12(瓶)
所以,能装满12瓶。
故答案为:B
3.B
【分析】物体所占空间的大小叫做它的体积;容积指箱子,油桶,仓库等所能容纳物体的体积。
【详解】题目中的“净含量”是指饮料瓶内实际装有的饮料量,即饮料本身的体积;
A.(饮料瓶的体积)是指瓶子本身占据的空间大小,与内部装的饮料量无关;
B.(饮料的体积)正确,因为“560mL”直接表示瓶中饮料的实际体积,符合“净含量”的定义;
C.(饮料瓶的容积)是指瓶子最多能容纳的液体体积,可能大于净含量(例如瓶子设计为600mL,但实际装560mL饮料)。
故答案为:B
4.B
【分析】每个小正方形的面积是1cm2,分别计算出立体图形的前、右、上三个面各有多少个小正方形,求出三者之和,即可知道露出的面积是多少。
【详解】1×1=1(cm2)
前面露出6个小正方形,右面露出6个小正方形,上面露出9个小正方形。
6+6+9=21(个)
21×1=21(cm2)
露在外面的面积是21cm2。
故答案为:B
5.A
【分析】11种正方体展开图:“141”型、“231”型、“222”型、“33”型 :
据此逐项判断即可。
【详解】根据分析可得:
A.不能折成正方体。
B.是正方体展开图 “141”型,能折成正方体。
C.是正方体展开图 “141”型,能折成正方体。
故答案为:A
6.A
【分析】长方体的体积=长×宽×高,把题目中这个长方体的长、宽、高代入公式计算,据此解答。
【详解】5×4×3
=20×3
=60(cm3)
所以,它的体积是60cm3。
故答案为:A
7.24
【分析】根据题意作图如下:
从图中可知:这个长方体恰好能裁成三个体积相等的正方体,底面是正方形,前后左右面就等于3×4=12(个)正方形面的大小,这个长方体表面积(84平方厘米)就相当于12+2=14(个)正方形面的大小。裁成三个相等的正方体,表面积就增加了4个正方形的面。用这个长方体的表面积÷14即可得一个正方形的面积,再乘4即可求出增加了的表面积。
【详解】84÷14×4=24(平方厘米)
这样表面积增加了24平方厘米。
8.4
【分析】根据题意,用一根铁丝焊接成一个长方体,则这根铁丝的长度就是长方体的棱长总和;根据长方体的棱长总和=(长+宽+高)×4,可知长方体的高=棱长总和÷4-长-宽,代入数据计算即可。
【详解】52÷4-6-3
=13-6-3
=4(厘米)
高是4厘米。
9.3
【分析】根据:长方体的体积=长×宽×高,池内水的高=容积÷(长×宽),据此计算。
【详解】84L=84dm3
84÷(7×4)
=84÷28
=3(dm)
所以池内水的高度是3dm。
10.240
【分析】要满足表面积增加的最大,沿原来长方体的最大面平行切开,表面积增加两个切面的面积,长方形的面积=长×宽,据此代入数据计算即可解答。
【详解】12×10×2
=120×2
=240(cm2)
表面积最大可增加240cm2。
11. 体积单位 升 毫升 L mL
【详解】容器所能容纳物体的体积,通常叫作它的容积。计量容积,一般就用体积单位。计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写成L和mL,1L=1000mL,容积单位和体积单位的关系:1L=1dm3,1mL=1cm3。
12.3
【分析】水面上升的体积就是这个石块的体积,长方体玻璃缸的长×宽×水面上升的高度=石块体积,据此列式计算。
【详解】5×3×(2.2-2)
=15×0.2
=3(dm3)
这个石块的体积是3dm3。
13.1.6
【分析】菜窖的深相当于长方体的高,根据长方体的高=容积÷长÷宽,列式计算即可。
【详解】高:40÷5÷5
=8÷5
=1.6(m)
所以应该挖1.6m深。
14.560平方厘米/560cm2/5.6平方分米/5.6dm2
【分析】根据正方形和长方形的特征可知,长方体前、后、左、右四个面相同,已知长和宽都是4分米,高是3.5厘米,先统一单位,然后根据长方形的面积公式,先求出1个面的面积再乘4即可求出前、后、左、右4个面的面积和。
【详解】4分米=40厘米
40×3.5×4
=140×4
=560(平方厘米)
长方体前、后、左、右四个面的面积之和是560平方厘米。
15.40
【分析】求需要铁丝的长度,就是求这个长方体棱长总和;已知一个底面周长是10cm,一个底面周长是2个长、2个宽的和,一个长方体有4条长,4条宽、4条高,用一个底面周长×2,求出4条长与4条宽的长度和,再用高×4,求出4条高的和,再把它们相加,即可解答。
【详解】10×2+5×4
=20+20
=40(cm)
至少需要40cm长的铁丝,才能做一个底面周长是10cm,高是5cm的长方体框架。
16.8
【分析】根据正方体的特征,12条棱都相等;那么拼成的大正方体的棱长最少由2个同样的小正方体的棱长组成,根据正方体体积:V=a3可以求出至少需要同样的小正方体的个数。
【详解】如图:
2×2×2
=4×2
=8(dm3)
8÷(1×1×1)
=8÷(1×1)
=8÷1
=8(个)
用棱长是1dm的小正方体摆成一个稍大的正方体,至少需要8个这样的小正方体。
17.96
【分析】分析题目,剩下物体的表面积等于棱长是4cm的正方体的表面积,据此结合正方体的表面积=棱长×棱长×6列式计算即可。
【详解】4×4×6
=16×6
=96(cm2)
正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是96cm2。
18. 3 12
【分析】从A点出发的对角线有AC、AF、AG、AH,其中AH 小于线段AB;
长方体有8个顶点,从每个顶点出发的情况是一样的。 从一个顶点出发可以连3条大于AB的线段,若直接用8×3=24来计算,会出现每条线段都被重复计算了2次的情况(因为一条线段有两个端点)。 所以长方体中大于AB的线段总数为8×3÷2=12条。
【详解】从A点出发的对角线有AC、AF、AG都大于AB;
前后面的对角线(4条),上下面的对角线(4条),AG、BH、EC、DF,一共有12条。
8×3÷2=12(条)
则“从A点出发可以连3条大于的线段,这个长方体中一共可以连12条大于的线段”。
19.×
【分析】根据上面的分析,棱台也有6个面、12条棱、8个顶点,棱台既不是长方体也不是正方体。据此分析判断。
【详解】据分析可知,有6个面、12条棱、8个顶点的物体不一定是长方体或正方体。原题说法错误。
故答案为:×
20.×
【分析】常见的容积单位有毫升、升,计量比较少的液体,通常用毫升作单位,1瓶可乐的容积差不多是300毫升,1升相当于2瓶矿泉水的容积。据此判断。
【详解】结合生活实际,冰箱容积一般用升作单位,所以原题说法错误。
故答案为:×
21.×
【分析】根据1 m3=1000 dm3,1 dm3=1000 cm3,高级单位换算成低级单位,乘进率,低级单位换算成高级单位,除以进率。先将所有数据都换算成以dm3为单位,再比较即可判断。
【详解】因为:4.06m3=4060 dm3
406000cm3=406 dm3
4060000cm3=4060 dm3
所以:4.06m3=4060 dm3=4060000cm3
4.06m3≠406000 dm3
在4.06m3、406000cm3、4060dm3、4060000cm3这4个数据中,4.06m3与4060dm3、4060000cm3相等,4.06m3与406000cm3不相等。因此原题说法不正确。
故答案为:×
22.√
【分析】体积表示物体所占空间的大小,不管怎么捏,橡皮泥是不会变少的,也就是说它的体积不会变小,于是捏成正方体后,体积依旧是原来的50立方厘米。
【详解】球形橡皮泥捏成一个正方体,形状虽然发生了变化,但它所占空间的大小一样,也就是体积没有发生变化,仍就是50立方厘米。原题干说法正确。
故答案为:√
【点睛】本题考查了体积的等积变形,明确同一个物体,形状无论怎么变化,体积始终保持不变。
23.√
【分析】根据体积的意义:物体所占空间的大小是物体的体积;把“千里马”熔化塑成了“拓荒牛”,可知只是两件工艺品的形状的变化,而体积没有变化。据此解答。
【详解】由分析可知:
蜡像厂把一个实心工艺品“千里马”熔化后,又在无损耗的情况下塑成了另一个实心工艺品“拓荒牛”,这两件工艺品中,“千里马”的体积等于“拓荒牛”的体积。原说法正确。
故答案为:√
24.27cm3;232cm3
【分析】左边:组合图形的体积=两个长方体体积之和,根据长方体的体积=长×宽×高,代入数据解答即可;
右边:组合图形的体积=长方体的体积-正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据解答即可。
【详解】5×3×1+2×2×3
=15+4×3
=15+12
=27(cm3)
8×6×5-2×2×2
=48×5-4×2
=240-8
=232(cm3)
左边组合图形的体积为27cm3,右边组合图形的体积为232cm3。
25.4厘米
【分析】两个相同的正方体木块拼成一个长方体,减少了8条棱长和,用32÷8,即可求出原来每个正方体木块的棱长。
【详解】32÷8=4(厘米)
答:原来每个正方体木块的棱长是4厘米。
26.36方
【分析】每根木料的体积=横截面积×长,木料总体积=每根的体积×500,据此计算。
【详解】2.4dm2=0.024m2
0.024×3×500
=0.072×500
=36(方)
答:这些木料一共是36方。
27.40.5升
【分析】根据1升=1立方分米,所以27升等于27立方分米,又知当水深3分米时,容器装了27升水,根据长方体的体积V=Sh,所以S=V÷h,再用长方体容器的底面积乘长方体容器的高,即可求出长方体容器能装满多少升的水。
【详解】27升=27立方分米
27÷3=9(平方分米)
9×4.5=40.5(立方分米)
40.5立方分米=40.5升
答:能装40.5升水。
28.12立方米
【分析】由于是石柱立着放入池中,放入水中的石柱高度是2米,根据,求出放入水中石柱的体积,放入水中石柱的体积就是溢出的水的体积,据此即可解答。
【详解】3×2×2=12(立方米)
答:水池溢出的水的体积是12立方米。
29.24平方分米
【分析】已知底面的周长是80厘米,底面是正方形,根据正方形的边长=周长÷4,因此边长为:80÷4=20厘米。这个长方体的框架,前后左右面4个面是形状大小相等的长方形,因此彩色纸的面积=前后左右面+上面=边长×高×4+边长×边长,据此代入数据计算,即可求出彩色纸的面积。再根据1平方分米=100平方厘米,将结果换算成平方分米。
【详解】80÷4=20(厘米)
20×25×4+20×20
=2000+400
=2400(平方厘米)
2400平方厘米=24平方分米
答:王师傅至少要买24平方分米的彩色纸。
30.4770块
【分析】根据1米=10分米,统一单位,砖墙的厚相当于长方体的宽,根据长方体体积=长×宽×高,求出砖墙的体积,砖墙的体积×每立方米用砖块数=砖的总块数,据此列式解答。
【详解】3分米=0.3米
15×0.3×2×530
=9×530
=4770(块)
答:林伯伯至少要准备4770块砖。
31.240立方米;576立方米
【分析】根据1米=100厘米,统一单位,煤渣和三合土的厚相当于长方体的高,根据长方体体积=长×宽×高,分别计算出煤渣、三合土的体积即可。
【详解】5厘米=0.05米、12厘米=0.12米
80×60×0.05=240(立方米)
80×60×0.12=576(立方米)
答:需要煤渣240立方米、三合土576立方米。
32.27立方分米;117立方分米
【分析】由题意可知,锯成的这个最大的正方体的棱长等于长方体的高,再根据长方体的体积=长×宽×高、正方体的体积=棱长×棱长×棱长分别求出长方体和正方体的体积,最后用长方体的体积减去锯成的正方体体积就是剩下部分的体积,据此解答即可。
【详解】3×3×3
=9×3
=27(立方分米)
8×6×3
=48×3
=144(立方分米)
144-27=117(立方分米)
答:这个正方体的体积是27立方分米,剩下部分的体积是117立方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
