(小升初择校分班考)小升初分班考高频考点押题卷-2024-2025学年五年级下册数学沪教版(含解析)
文档属性
| 名称 | (小升初择校分班考)小升初分班考高频考点押题卷-2024-2025学年五年级下册数学沪教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 382.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学小升初分班考高频考点押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.把下图这张六连块纸板围折成一个正方体,一只蚂蚁沿正方体表面从E点爬至F点,最短的路线是( )。
A. B. C. D.
2.一个长方体的长、宽、高分别是a厘米、b厘米和h厘米,如果长方体的长和高不变,宽增加3厘米,长方体的体积增加( )立方厘米。
A.3ah B.3abh C.abh D.3b
3.盒子里有红、黄、绿三种颜色的小球共20个,它们除颜色外都相同。任意摸一个球,要使摸到红球的可能性最小,那么盒中最多有( )个红球。
A.5 B.6 C.7 D.8
4.下列各句话中有( )句是错误的。
①如果电梯停在地上一层记作“0层”,上升记为正。那么“﹣1层”表示电梯停在地下一层:“﹢1层”表示电梯停在地上二层。
②“地球上太阳从西面升起”是不确定事件。
③平行线之间的线段处处相等。
④一个两位数,十位数字为m,个位数字为n,这个两位数可以表示为mn。
A.1 B.2 C.3 D.4
5.食品包装盒上标有“净含量300±3克”,质检员随机抽检了5盒食品,净含量分别是297克,292克,305克,302克,303克,不合格产品有( )盒。
A.1 B.2 C.3 D.4
6.一个正方形的6个面分别写上1,2,3,4,5,6,随意抛落后,朝上面的数字( )。
A.单数的可能性大 B.双数的可能性大 C.每个数字的可能性一样大
7.商店运来苹果和梨共120千克,苹果重量比梨的2倍还多12千克,两种水果各重________千克。(用方程解)。
A.梨36千克,苹果84千克 B.梨24千克,苹果96千克
C.梨30千克,苹果90千克
8.甲乙两地间的公路长336千米,两辆汽车从两地同时相对开出,经过3.5小时在途中相遇。已知甲地开出的汽车每小时行52千米,乙地开出的汽车每小时行( )。
A.48千米 B.44千米 C.42千米
二、填空题。(每空1分,共20分)
9.有一块棱长10分米的正方体钢材,把它锻造成长25分米,宽10分米的长方体钢材,锻造成的钢材高是( )厘米。(不计损耗)
10.如图,一个正方体的展开图,2号面相对的是( )号面;4号面相对的是( )号面。
11.把一张正方形的纸剪成若干个小正方形。 如果剪成边长为2厘米的小正方形,剪出的小正方形的个数比剪成边长为3厘米的小正方形多20个,两种剪法都正好用完纸,原来这张正方形纸的面积是( )平方厘米。
12.口袋中放着7个同样的塑料球,上面分别标有﹣1、0、3、﹣4、6、﹣5、10,甲乙两人做游戏,规定摸出1个球,若球号码是自然数,甲得1分;摸出的球号码不是自然数,乙得1分。( )得分的机会多。
13.有唱歌卡片7张,跳舞卡片5张,讲故事卡片2张,有( )种可能,抽到( )卡片的可能性最小。
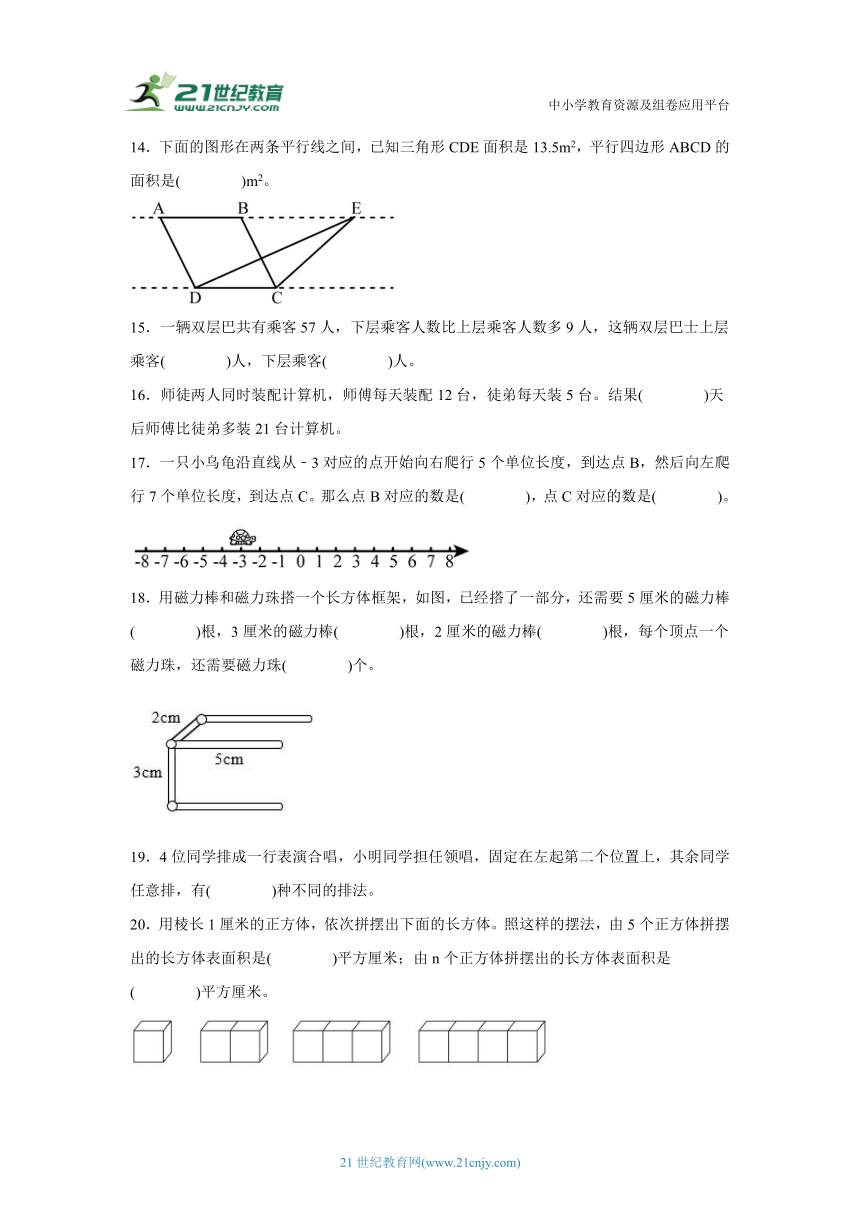
14.下面的图形在两条平行线之间,已知三角形CDE面积是13.5m2,平行四边形ABCD的面积是( )m2。
15.一辆双层巴共有乘客57人,下层乘客人数比上层乘客人数多9人,这辆双层巴士上层乘客( )人,下层乘客( )人。
16.师徒两人同时装配计算机,师傅每天装配12台,徒弟每天装5台。结果( )天后师傅比徒弟多装21台计算机。
17.一只小乌龟沿直线从﹣3对应的点开始向右爬行5个单位长度,到达点B,然后向左爬行7个单位长度,到达点C。那么点B对应的数是( ),点C对应的数是( )。
18.用磁力棒和磁力珠搭一个长方体框架,如图,已经搭了一部分,还需要5厘米的磁力棒( )根,3厘米的磁力棒( )根,2厘米的磁力棒( )根,每个顶点一个磁力珠,还需要磁力珠( )个。
19.4位同学排成一行表演合唱,小明同学担任领唱,固定在左起第二个位置上,其余同学任意排,有( )种不同的排法。
20.用棱长1厘米的正方体,依次拼摆出下面的长方体。照这样的摆法,由5个正方体拼摆出的长方体表面积是( )平方厘米;由n个正方体拼摆出的长方体表面积是( )平方厘米。
三、判断题。(每题1分,共5分)
21.在长方体的所有棱中,至少有4条棱的长度是相等的。( )
22.数轴上,离开﹢3这个点4个单位长度的点所表示的数是﹣1和7。( )
23.正方体的棱长扩大2倍,它的棱长之和就扩大24倍。( )
24.某一天的气温是﹣5℃~5℃,最高气温和最低气温是一样的。( )
25.小宇抛100次硬币,正面和反面朝上的次数肯定会一样。( )
四、计算题。(共25分)
26.直接写出得数。(共10分)
0.75-0.57= 6.3÷10= 5.6+0.44= 2-1.09= 40÷1000=
3.27+5.83= 25×4÷25×4= 9.99-9.9= 5.6-1.7-0.3= 3.08×100÷10=
27.用递等式计算。(能简算的要简算。共6分)
28.解方程。(共8分)
29.求组合体的体积。(单位:厘米,共3分)
五、操作题。(共6分)
30.在下面圆盘上涂上红色、绿色和黄色。
(1)指针停在红色区域的可能性大。
(2)指针停在绿色区域的可能性分别是停在红色和黄色区域的2倍。
(3)指针停在红色、绿色和黄色三种颜色区域的可能性都一样。
六、解答题。(每题6分,共36分)
31.小丁丁8:00出门,以每分钟60米的速度从家步行去学校,8:15即可到达。出发9分钟后,爸爸发现他的作业遗漏在家里了,沿路骑自行车以每分钟180米的速度追他,爸爸能在小丁丁到达前追上他吗?
32.学校给用餐学生安排座位,如果每张餐桌坐12人,那么空出4张餐桌;如果每张餐桌坐10人,那么正好坐满,学校共有几张餐桌?用餐学生共有多少人?
33.小巧和小亚在学校操场的跑道上散步,跑道一周长400米,小巧平均每分钟行60米,小亚平均每分钟行65米。两人从同一地点出发,小巧先行2.5分钟后小亚再出发,两人背向而行,经过几分钟两人相遇?
34.图书馆新到一批图书,要平均放在几个新书架上,如果每个书架放60本,那么还缺2个书架;如果每个书架放68本,那么正好放完,一共有几个新书架?这批图书共有多少本?
35.味美糕点店中秋节来临之际,将一天加工好的月饼装入右面的礼盒中(两种礼盒个数相同)。若都装入6枚装的礼盒中,多出35枚月饼;若都装入8枚装的礼盒中,还缺55枚月饼。则糕点店里两种礼盒各有多少个?这一天一共加工了多少枚月饼?
36.有甲、乙两个长方体容器,从甲容器内部量得长、宽、高分别为40厘米、10厘米、10厘米。将甲容器的右面作为底面,直立起来就是乙容器,已知甲容器中装有水,将其倾斜,水面刚好如下图所示。乙容器是空的。
(1)甲容器中水的体积是多少?
(2)现在把甲、乙两个容器放在同一桌面上,将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,那么乙容器中需要倒入多少毫升水?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.D
【分析】根据两点之间直线最短,在平面图形上连接这两点,即为最短的路径,据此解答。
【解析】如图:
所以符合题意是。
故答案为:D
2.A
【分析】根据长方体体积公式:体积=长×宽×高;计算出原来的长方体的体积,宽增加3厘米,即宽为(b+3)厘米,代入长方体体积公式,求出增加后长方体的体积,再减去原来长方体的体积,即可解答。
【解析】原来长方体的体积:a×b×h=abh(立方厘米)
宽增加3厘米后长方体的体积:
a×(b+3)×h
= a×h×(b+3)
=abh+3ah(立方厘米)
abh+3ah-abh
= abh-abh+3ah
=3ah(立方厘米)
则长方体的体积增加3ah立方厘米。
故答案为:A
3.B
【分析】根据各种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大,据此解答即可。
【解析】红、黄、绿三种颜色的小球共20个,任意摸一个球,要使摸到红球的可能性最小,则红球的个数<黄球的个数=绿球的个数,根据平均分的定义可知红球不能是7个或7个以上那么最多有6个。
故答案为:B
【点评】解答此题应结合题意,并考虑可能性的大小,进行分析、解答即可。
4.C
【分析】①根据负数的意义,上升记为“﹢”,则下降记为“﹣”,所以“﹢4层”表示电梯上升4层,此时电梯停在地上五层,据此判定即可;
②确定事件包括必然事件和不可能事件,必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件;据此判断;
③因为平行线之间的距离都是两条平行线的垂线段,所以处处相等;据此解答;
④该两位数的十位上的数字是m,表示m个10,个位上的数字是n,表示n个1,求这个两位数,把m个10和n个1相加即可。
【解析】①如果电梯停在地上一层记作“0层”,上升记为正。那么“﹣1层”表示电梯停在地下一层:“﹢1层”表示电梯停在地上一层,原题说法错误;
②“地球上太阳从西面升起”是不可能事件,原题说法错误;
③两条平行线之间的距离处处相等;原题说法正确;
④10×m+1×n
=10m+n
所以这个两位数用含有字母的式子表示是(10m+n);原题说法错误。
说法错误的有:①②④,共3个;
故答案为:C
【点评】此题主要考查了负数的意义及其应用、用字母表示数的方法、必然事件、不可能事件、随机事件的概念以及平行线之间的距离处处相等,应灵活掌握和运用。
5.B
【分析】此题主要用正负数来表示具有意义相反的两种量:选300克为标准记为0,超过部分为正,不足的部分为负,在﹢3克和﹣3克之间的都是合格,否则,即为不合格。
【解析】300-3=297(克)
300+3=303(克)
297克≤合格产品的净含量≤303克,净含量为297克、302克、303克的是合格产品,净含量为292克、305克的是不合格产品,所以不合格产品有2盒。
故答案为:B
【点评】此题首先要知道以谁为标准,规定超出标准的为正,低于标准的为负,由此用正负数解答问题。
6.C
【分析】每个数都只有1个,所以每个数朝上的概率是一样的;奇数有1、3、5,偶数有2、4、6,都是3个,所以奇数和偶数朝上的概率也是一样的。
【解析】正方体的6个面除了数字不同,没有其他不同,每个面朝上的概率是一样的。
故答案为:C
【点评】当条件对事件的发生有利时,发生的可能性就大一些。当条件对事件的发生不利时,发生的可能性就小一些。
7.A
【分析】根据题意可知,设运来梨x千克,苹果重量比梨的2倍还多12千克,即苹果的质量×2+12千克=苹果的质量,即运来苹果(2x+12)千克,再用梨的质量+苹果的质量=运来的梨和苹果的总质量,列方程:x+(2x+12)=120,解方程,即可解答。
【解析】解:设运来梨x千克,则苹果(2x+12)千克。
x+(2x+12)=120
x+2x+12=120
3x=120-12
3x=108
x=108÷3
x=36
苹果:36×2+12
=72+12
=84(千克)
商店运来苹果和梨共120千克,苹果重量比梨的2倍还多12千克,两种水果各重梨36千克,苹果84千克。
故答案为:A
【点评】本题考查方程的实际应用,利用运来梨的质量与苹果的质量与总质量之间的关系,设出未知数,找出相关的量,列方程,解方程。
8.B
【分析】根据题意可知,设乙地开出的汽车每小时行x千米,用(甲地开出的汽车速度+乙地开出的汽车速度)×相遇时间=甲、乙两地之间的公路长度,据此列方程解答。
【解析】解:设乙地开出的汽车每小时行x千米,
(52+x)×3.5=336
(52+x)=336÷3.5
52+x=96
x=96-52
x=44
故答案为:B
【点评】本题考查相遇问题,根据题意,找出相关的量,列方程,解方程。
9.40
【分析】根据正方体的体积=棱长×棱长×棱长,代入数据求出正方体的体积,也就是长方体钢材的体积,根据长方体的体积=长×宽×高,用长方体的体积除以长,再除以宽即可求出高是多少分米,再根据1分米=10厘米,把分米化成厘米即可。
【解析】10×10×10÷25÷10
=100×10÷25÷10
=1000÷25÷10
=40÷10
=4(分米)
4分米=40厘米
所以锻造成的钢材高是40厘米。
10.4 2
【分析】
根据正方体的展开图知识,属于“1-3-2型”,折成正方体后,有公共边的两个面相邻,没有公共边的两个面相对。1号面相对的是5号面;2号面相对的是4号面,3号面相对的是6号面。
【解析】由分析可知:
如图,一个正方体的展开图,2号面相对的是4号面;4号面相对的是2号面。
11.144
【分析】设可剪成边长为2厘米的小正方形x个,则剪成边长为3厘米的小正形(x-20)个,根据边长为2厘米的小正方形的面积和等于边长为3厘米的小正方形的面积和,据此列方程解答。再用所得解乘边长为2厘米的小正方形的面积,即可得到这张纸的面积。
【解析】解:设可剪成边长为2厘米的小正方形x个,则剪成边长为3厘米的小正形(x-20)个。
(平方厘米)
原来这张正方形纸的面积是144平方厘米。
12.甲
【分析】﹣1、0、3、﹣4、6、﹣5、10这7个数中,自然数有0、3、6、10,共4个,不是自然数的有个;可能性的大小由事件出现的次数多少来决定,据此解答即可。
【解析】自然数有0、3、6、10,共4个,不是自然数的有个,摸出自然数的可能性大一些,所以甲得分的机会多。
13.3/三 讲故事
【分析】任意摸出一张,可能有3种结果即:唱歌卡片、跳舞卡片、讲故事卡片;因为讲故事卡片的个数最少,所以摸出讲故事卡片的可能性最小。
【解析】7>5>2
摸出的卡片颜色有3种可能,摸出讲故事卡片的可能性最小。
【点评】解答此题应根据题意,并根据可能性的求法,进行分析,也可以根据各种卡片的数量进行比较,即可得出结论。
14.27
【分析】根据“平行线之间的距离处处相等”,观察图形可知,三角形CDE与平行四边形ABCD等底等高;再根据“三角形的面积是与其等底等高的平行四边形面积的一半”,据此可知:已知三角形的面积,用三角形的面积乘2,即可求出与三角形等底等高的平行四边形的面积;据此解题即可。
【解析】13.5×2=27(m2)
所以平行四边形ABCD的面积是27m2。
【点评】解答此题的主要依据是:等底等高的三角形和平行四边形的面积的关系。
15.24 33
【分析】根据题意,可得到等量关系式:下层人数+上层人数=57,由此可设上层乘客数是x人,则下层乘客数是x+9人,再根据一共是57人,列出方程解答。
【解析】解:设上层乘客数是x人,则下层乘客数是x+9人
x+(x+9)=57
2x+9=57
2x=57-9
2x=48
x=48÷2
x=24
24+9=33(人)
上层有乘客24人,下层有33人。
【点评】关键是根据题意设出未知数,再找出数量关系等式,列出方程解答。
16.3
【分析】设x天后师傅比徒弟多装21台计算机,师傅每天装配12台,x天装配12x台;徒弟每天装5台,x天装5x台,师傅比徒弟多装21台计算机,即师傅装的计算机的台数-徒弟装的计算机的台数=21台,列方程:12x-5x=21,解方程,即可解答。
【解析】解:设x天后师傅比徒弟多装21台计算机。
12x-5x=21
7x=21
x=21÷7
x=3
师徒两人同时装配计算机,师傅每天装配12台,徒弟每天装5台。结果3天后师傅比徒弟多装21台计算机。
【点评】本题考查方程的实际应用。利用师傅和徒弟装计算机天数和计算机台数的关系,设出未知数,找出相关的量,列方程,解方程。
17.2 ﹣5
【分析】在数轴上,从﹣3对应的点向右数5个单位长度就是点B的位置,再从点B向左数7个单位长度就是点C的位置,写出点B、C对应的数即可。
【解析】一只小乌龟沿直线从﹣3对应的点开始向右爬行5个单位长度,到达点B,然后向左爬行7个单位长度,到达点C。那么点B对应的数是2,点C对应的数是﹣5。
【点评】本题考查正负数在数轴上的认识,根据题意数清格数即可。
18.1 3 3 5
【分析】长方体有12条棱,12条棱可以分3组:4条长,4条宽,4条高,长、宽、高分别相等。有8个顶点,每个顶点处由长、宽、高三条棱组成。据此可知,5厘米的长已经有3根,还差1根,3厘米的高有1根,还差3根,2厘米的宽有1根,还差3根,顶点已经有3个,还差5个。
【解析】4-3=1(根)
4-1=3(根)
8-3=5(个)
用磁力棒和磁力珠搭一个长方体框架,如图,已经搭了一部分,还需要5厘米的磁力棒1根,3厘米的磁力棒3根,2厘米的磁力棒3根,每个顶点一个磁力珠,还需要磁力珠5个。
【点评】本题根据长方体的特征解答。
19.6
【分析】小明同学担任领唱,位置固定,第二位同学有3个位置可以选择,第三位同学有2个位置可以选择,第四位同学有1个位置可以选择,据此利用乘法原理计算。
【解析】3×2×1=6(种)
即有6种不同的排法。
【点评】掌握在排列组合中乘法原理的应用是解答题目的关键。
20.22 4n+2
【分析】棱长为1厘米的正方体的一个面的面积是1平方厘米,且相邻的2个正方体拼组在一起减少了2个小正方体的面:
第一个长方体的表面积是:6个小正方体的面,可以写成1×4+2;
第二个长方体的表面积是:10个小正方体的面,可以写成2×4+2;
第三个长方体的表面积是:14个小正方体的面,可以写成3×4+2;
第五个长方体的表面积是:22个小正方体的面,可以写成5×4+2;
…
则第n个长方体的表面积是:4n+2个小正方体的面。
【解析】根据题干分析可得:
第五个长方体的表面积是:
5×4+2
=20+2
=22(平方厘米)
第n个长方体的表面积是:4n+2个小正方体的面。
【点评】主要考查了找规律,解答此题关键是首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。
21.√
【分析】长方体的特征:长方体有12条棱,相对的四条棱长度相等,即长、宽、高各有4条;如果长方体六个面中有两个面是正方形时,则会出现更多长度相等的棱。
【解析】在长方体的所有棱中,至少有4条棱的长度是相等的。
原题说法正确。
故答案为:√
22.√
【分析】在数轴上,到﹢3点单位长度的点分别在该点的左边和右边两种情况,据此解答。
【解析】4-3=1
4+3=7
数轴上,离开﹢3这个点4个单位长度的点所表示的数是﹣1和7。
原题干说法正确。
故答案为:√
【点评】本题主要考查对数轴的认识,解题时注意离开﹢3点单位长度的点有两种情况,不要漏解。
23.×
【分析】设扩大前正方体的棱长为a,扩大后的棱长为2a;根据正方体棱长总和公式:正方体棱长总和=棱长×12;求出扩大前正方体棱长总和和扩大后正方体棱长总和,进而解答。
【解析】设扩大前正方体棱长为a,扩大后正方体棱长为2a。
(2a×12)÷(a×12)
=24a÷12a
=2
正方体的棱长扩大2倍,它的棱长之和就扩大2倍。
原题干说法错误。
故答案为:×
【点评】熟练掌握正方体棱长总和公式是解答本题的关键。
24.×
【分析】最高气温是5℃,是一个正数。最低气温是﹣5℃,是一个负数。任何一个负数都比正数小,据此判断即可。
【解析】﹣5℃<5℃
则最低气温要小于最高气温,题干说法错误。
故答案为:×
【点评】本题考查正负数比较大小的方法。任何一个正数都比0大,任何一个负数都比0小,任何一个负数都比正数小。
25.×
【分析】硬币有两面,正面和反面。每次抛硬币,可能正面朝上,也可能反面朝上,且每次得到的结果与之前得到的结果无关,据此判断即可。
【解析】小宇抛100次硬币,正面和反面朝上的次数不一定相同,可能正面朝上的次数多,也可能反面朝上的次数多,也可能两个结果的次数相同。
故答案为:×
【点评】本题考查时间的确定性和不确定性,关键是明确每次抛硬币都是一次全新的实验,结果与之前的结果无关。
26.0.18;0.63;6.04;0.91;0.04
9.1;16;0.09;3.6;30.8
【解析】略
27.15;738;1.08
【分析】(1)运用加法交换律和加法结合律简算;
(2)运用乘法分配律简算;
(3)根据小数四则混合运算的顺序,先算除法,再算减法,接着算加法,最后算乘法。
【解析】
=(5.6+4.4)+(0.78+4.22)
=10+5
=15
=7.38×(99+1)
=7.38×100
=738
=
=
=0.9×1.2
=1.08
28.x=302;x=18;x=2;x=14
【分析】(1)根据等式的基本性质两边同时加上10,再同时除以5即可;
(2)方程左边简化为0.4+0.2x,然后根据等式的基本性质等式两边同时减去0.4,然后再同时除以0.2即可;
(3)方程左边简化为0.5x,然后根据等式的基本性质等式两边同时除以0.5即可;
(4)根据等式的基本性质等式两边同时加上2x,然后同时减去7,最后同时除以2即可。
【解析】
解:5x-10+10=1500+10
5x=1510
5x÷x=1510÷5
x=302
(2)
解:0.4+0.2x=4
0.4+0.2x-0.4=4-0.4
0.2x=3.6
0.2x÷0.2=3.6÷0.2
x=18
(3)
解:0.5x=1
0.5x÷0.5=1÷0.5
x=2
(4)
解:35-2x+2x=7+2x
7+2x=35
7+2x-7=35-7
2x=28
2x÷2=28÷2
x=14
29.156立方厘米
【分析】
如图,组合体的体积等于两个长方体的体积和,长方体体积公式:V=abh,据此分别计算出两个长方体的体积,相加即可。
【解析】V1=abh
=10×4×(6-3)
=40×3
=120(立方厘米)
V2=abh
=3×3×4
=36(立方厘米)
V=V1+V2=120+36=156(立方厘米)
这个组合体的体积是156立方厘米。
30.见详解
【分析】由图可知,每个转盘上等分了8份
(1)要使指针停在红色区域的可能性大,则涂红色的份数最多,可涂4份红色、2份黄色、2份绿色;
(2)要使指针停在绿色区域的可能性分别是红色和黄色的2倍,则可涂2份红色、2份黄色、4份绿色;
(3)要使指针停在绿色、红色、黄色区域的可能性都一样,则可涂2份红色、2份黄色、2份绿色、2份蓝色;据此涂色即可。
【解析】根据分析作图如下:
【点评】解答此题关键是根据题目要求及可能性的大小确定出各种颜色要涂几份。
31.能
【分析】设经过x分钟后爸爸追上小丁丁;根据路程=速度×时间,小丁丁每分钟60米,先求出小丁丁9分钟走的路程,列式为60×9;再求走x分钟行的路程,即60x米;爸爸骑自行车每分钟180米,x分钟爸爸行了180x米;小丁丁走的路程=爸爸骑自行车行的路程,列方程:60×9+60x=180x,解方程,求出经过多少分钟爸爸追上小丁丁,再加上9分钟,求出小丁丁走的时间;再和小丁丁上学的时间比较,如果大于小丁丁上学用的时间,爸爸不能在小丁丁到达学校前追上,如果小于小丁丁上学用的时间,爸爸能在小丁丁到达学校前追上,据此解答。
【解析】8:15-8:00=15(分钟)
解:设经过x分钟后爸爸追上小丁丁。
60×9+60x=180x
540+60x=180x
540+60x-60x=180x-60x
120x=540
120x÷120=540÷120
x=4.5
4.5+9=13.5(分钟)
13.5分钟<15分钟,爸爸能在小丁丁到达前追上他。
答:爸爸能在小丁丁到达前追上他。
32.24张;240人
【分析】根据题意,可以设学校共有张餐桌;如果每张餐桌坐12人,那么空出4张餐桌,则用餐学生共有(12-12×4)人;如果每张餐桌坐10人,那么正好坐满,则用餐学生共有10人。根据用餐学生人数不变,据此列出方程,并求解。
【解析】解:设学校共有张餐桌。
12-12×4=10
12-48=10
12=10+48
12-10=48
2=48
=48÷2
=24
10×24=240(人)
答:学校共有24张餐桌,用餐学生共有240人。
33.2分钟
【分析】设经过x分钟两人相遇;根据速度×时间=路程,用小巧的速度×2.5分钟,求出小巧2.5分钟行的路程,小巧平均每分钟行60米,x分钟行60x米;小亚每分钟行65米,x分钟行65x米,小巧现行的2.5分钟的路程+小巧x分钟行的路程+小亚x分钟行的路程=跑道一周的长度,列方程:60×2.5+60x+65x=400,解方程,即可解答。
【解析】解:设经过x分钟两人相遇。
60×2.5+60x+65x=400
150+60x+65x=400
150+125x-150=400-150
125x=250
125x÷125=250÷125
x=2
答:经过2分钟两人相遇。
34.15个;1020本
【分析】设一共有x个新书架,如果每个书架放60本,那么还缺2个书架,即每个书架放60本,需要(x+2)个书架,根据每个书架放的本数×书架个数=总本数,列出方程求出x的值是新书架个数,通过新书架个数再求出图书总本数即可。
【解析】解:设一共有x个新书架。
60×(x+2)=68x
60x+120=68x
60x+120-60x =68x-60x
8x=120
8x÷8=120÷8
x=15
68×15=1020(本)
答:一共有15个新书架,这批图书共有1020本。
35.45个;305枚
【分析】设糕点店里两种礼盒各有x个,若用6枚装的礼盒,则月饼的总个数表示为(6x+35)个;若用8枚装的礼盒,则月饼的总个数表示为(8x-55)个。根据两种包装下,月饼的总个数相等,列出方程。
【解析】解:设糕点店里两种礼盒各有x个。
6x+35=8x-55
35+55=8x-6x
90=2x
x=90÷2
x=45
6×45+35
=270+35
=305(枚)
答:糕点店里两种礼盒各有45个,这一天一共加工了305枚月饼。
【点评】此题考查了盈亏问题。在分配问题中(“盈不足问题”),因为分配的总量不变,可由不同的分配方法表示出同一种量,进而列出方程求解。
36.(1)2000立方厘米
(2)400毫升
【分析】(1)从图中可以看出,甲容器装水的体积等于甲容器体积的一半,根据长方体的体积公式V=abh,代入数据计算求解。
(2)从图中可知,甲容器的底面积是(40×10)平方厘米;将甲容器的右面作为底面,直立起来就是乙容器,则乙容器的底面积是(10×10)平方厘米;
将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,则水的体积不变,水的高度一样,那么可以把甲、乙两个容器看作一个底面积为甲、乙两个底面积之和的容器;
根据长方体的高h=V÷S,代入数据计算求出容器中水的高度;再根据长方体的体积公式V=abh,求出乙容器中水的体积。注意单位的换算:1立方厘米=1毫升。
【解析】(1)40×10×10÷2
=400×10÷2
=4000÷2
=2000(立方厘米)
答:甲容器中水的体积是2000立方厘米。
(2)2000÷(40×10+10×10)
=2000÷(400+100)
=2000÷500
=4(厘米)
10×10×4
=100×4
=400(立方厘米)
400立方厘米=400毫升
答:乙容器中需要倒入400毫升水。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学小升初分班考高频考点押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.把下图这张六连块纸板围折成一个正方体,一只蚂蚁沿正方体表面从E点爬至F点,最短的路线是( )。
A. B. C. D.
2.一个长方体的长、宽、高分别是a厘米、b厘米和h厘米,如果长方体的长和高不变,宽增加3厘米,长方体的体积增加( )立方厘米。
A.3ah B.3abh C.abh D.3b
3.盒子里有红、黄、绿三种颜色的小球共20个,它们除颜色外都相同。任意摸一个球,要使摸到红球的可能性最小,那么盒中最多有( )个红球。
A.5 B.6 C.7 D.8
4.下列各句话中有( )句是错误的。
①如果电梯停在地上一层记作“0层”,上升记为正。那么“﹣1层”表示电梯停在地下一层:“﹢1层”表示电梯停在地上二层。
②“地球上太阳从西面升起”是不确定事件。
③平行线之间的线段处处相等。
④一个两位数,十位数字为m,个位数字为n,这个两位数可以表示为mn。
A.1 B.2 C.3 D.4
5.食品包装盒上标有“净含量300±3克”,质检员随机抽检了5盒食品,净含量分别是297克,292克,305克,302克,303克,不合格产品有( )盒。
A.1 B.2 C.3 D.4
6.一个正方形的6个面分别写上1,2,3,4,5,6,随意抛落后,朝上面的数字( )。
A.单数的可能性大 B.双数的可能性大 C.每个数字的可能性一样大
7.商店运来苹果和梨共120千克,苹果重量比梨的2倍还多12千克,两种水果各重________千克。(用方程解)。
A.梨36千克,苹果84千克 B.梨24千克,苹果96千克
C.梨30千克,苹果90千克
8.甲乙两地间的公路长336千米,两辆汽车从两地同时相对开出,经过3.5小时在途中相遇。已知甲地开出的汽车每小时行52千米,乙地开出的汽车每小时行( )。
A.48千米 B.44千米 C.42千米
二、填空题。(每空1分,共20分)
9.有一块棱长10分米的正方体钢材,把它锻造成长25分米,宽10分米的长方体钢材,锻造成的钢材高是( )厘米。(不计损耗)
10.如图,一个正方体的展开图,2号面相对的是( )号面;4号面相对的是( )号面。
11.把一张正方形的纸剪成若干个小正方形。 如果剪成边长为2厘米的小正方形,剪出的小正方形的个数比剪成边长为3厘米的小正方形多20个,两种剪法都正好用完纸,原来这张正方形纸的面积是( )平方厘米。
12.口袋中放着7个同样的塑料球,上面分别标有﹣1、0、3、﹣4、6、﹣5、10,甲乙两人做游戏,规定摸出1个球,若球号码是自然数,甲得1分;摸出的球号码不是自然数,乙得1分。( )得分的机会多。
13.有唱歌卡片7张,跳舞卡片5张,讲故事卡片2张,有( )种可能,抽到( )卡片的可能性最小。
14.下面的图形在两条平行线之间,已知三角形CDE面积是13.5m2,平行四边形ABCD的面积是( )m2。
15.一辆双层巴共有乘客57人,下层乘客人数比上层乘客人数多9人,这辆双层巴士上层乘客( )人,下层乘客( )人。
16.师徒两人同时装配计算机,师傅每天装配12台,徒弟每天装5台。结果( )天后师傅比徒弟多装21台计算机。
17.一只小乌龟沿直线从﹣3对应的点开始向右爬行5个单位长度,到达点B,然后向左爬行7个单位长度,到达点C。那么点B对应的数是( ),点C对应的数是( )。
18.用磁力棒和磁力珠搭一个长方体框架,如图,已经搭了一部分,还需要5厘米的磁力棒( )根,3厘米的磁力棒( )根,2厘米的磁力棒( )根,每个顶点一个磁力珠,还需要磁力珠( )个。
19.4位同学排成一行表演合唱,小明同学担任领唱,固定在左起第二个位置上,其余同学任意排,有( )种不同的排法。
20.用棱长1厘米的正方体,依次拼摆出下面的长方体。照这样的摆法,由5个正方体拼摆出的长方体表面积是( )平方厘米;由n个正方体拼摆出的长方体表面积是( )平方厘米。
三、判断题。(每题1分,共5分)
21.在长方体的所有棱中,至少有4条棱的长度是相等的。( )
22.数轴上,离开﹢3这个点4个单位长度的点所表示的数是﹣1和7。( )
23.正方体的棱长扩大2倍,它的棱长之和就扩大24倍。( )
24.某一天的气温是﹣5℃~5℃,最高气温和最低气温是一样的。( )
25.小宇抛100次硬币,正面和反面朝上的次数肯定会一样。( )
四、计算题。(共25分)
26.直接写出得数。(共10分)
0.75-0.57= 6.3÷10= 5.6+0.44= 2-1.09= 40÷1000=
3.27+5.83= 25×4÷25×4= 9.99-9.9= 5.6-1.7-0.3= 3.08×100÷10=
27.用递等式计算。(能简算的要简算。共6分)
28.解方程。(共8分)
29.求组合体的体积。(单位:厘米,共3分)
五、操作题。(共6分)
30.在下面圆盘上涂上红色、绿色和黄色。
(1)指针停在红色区域的可能性大。
(2)指针停在绿色区域的可能性分别是停在红色和黄色区域的2倍。
(3)指针停在红色、绿色和黄色三种颜色区域的可能性都一样。
六、解答题。(每题6分,共36分)
31.小丁丁8:00出门,以每分钟60米的速度从家步行去学校,8:15即可到达。出发9分钟后,爸爸发现他的作业遗漏在家里了,沿路骑自行车以每分钟180米的速度追他,爸爸能在小丁丁到达前追上他吗?
32.学校给用餐学生安排座位,如果每张餐桌坐12人,那么空出4张餐桌;如果每张餐桌坐10人,那么正好坐满,学校共有几张餐桌?用餐学生共有多少人?
33.小巧和小亚在学校操场的跑道上散步,跑道一周长400米,小巧平均每分钟行60米,小亚平均每分钟行65米。两人从同一地点出发,小巧先行2.5分钟后小亚再出发,两人背向而行,经过几分钟两人相遇?
34.图书馆新到一批图书,要平均放在几个新书架上,如果每个书架放60本,那么还缺2个书架;如果每个书架放68本,那么正好放完,一共有几个新书架?这批图书共有多少本?
35.味美糕点店中秋节来临之际,将一天加工好的月饼装入右面的礼盒中(两种礼盒个数相同)。若都装入6枚装的礼盒中,多出35枚月饼;若都装入8枚装的礼盒中,还缺55枚月饼。则糕点店里两种礼盒各有多少个?这一天一共加工了多少枚月饼?
36.有甲、乙两个长方体容器,从甲容器内部量得长、宽、高分别为40厘米、10厘米、10厘米。将甲容器的右面作为底面,直立起来就是乙容器,已知甲容器中装有水,将其倾斜,水面刚好如下图所示。乙容器是空的。
(1)甲容器中水的体积是多少?
(2)现在把甲、乙两个容器放在同一桌面上,将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,那么乙容器中需要倒入多少毫升水?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.D
【分析】根据两点之间直线最短,在平面图形上连接这两点,即为最短的路径,据此解答。
【解析】如图:
所以符合题意是。
故答案为:D
2.A
【分析】根据长方体体积公式:体积=长×宽×高;计算出原来的长方体的体积,宽增加3厘米,即宽为(b+3)厘米,代入长方体体积公式,求出增加后长方体的体积,再减去原来长方体的体积,即可解答。
【解析】原来长方体的体积:a×b×h=abh(立方厘米)
宽增加3厘米后长方体的体积:
a×(b+3)×h
= a×h×(b+3)
=abh+3ah(立方厘米)
abh+3ah-abh
= abh-abh+3ah
=3ah(立方厘米)
则长方体的体积增加3ah立方厘米。
故答案为:A
3.B
【分析】根据各种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大,据此解答即可。
【解析】红、黄、绿三种颜色的小球共20个,任意摸一个球,要使摸到红球的可能性最小,则红球的个数<黄球的个数=绿球的个数,根据平均分的定义可知红球不能是7个或7个以上那么最多有6个。
故答案为:B
【点评】解答此题应结合题意,并考虑可能性的大小,进行分析、解答即可。
4.C
【分析】①根据负数的意义,上升记为“﹢”,则下降记为“﹣”,所以“﹢4层”表示电梯上升4层,此时电梯停在地上五层,据此判定即可;
②确定事件包括必然事件和不可能事件,必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件;据此判断;
③因为平行线之间的距离都是两条平行线的垂线段,所以处处相等;据此解答;
④该两位数的十位上的数字是m,表示m个10,个位上的数字是n,表示n个1,求这个两位数,把m个10和n个1相加即可。
【解析】①如果电梯停在地上一层记作“0层”,上升记为正。那么“﹣1层”表示电梯停在地下一层:“﹢1层”表示电梯停在地上一层,原题说法错误;
②“地球上太阳从西面升起”是不可能事件,原题说法错误;
③两条平行线之间的距离处处相等;原题说法正确;
④10×m+1×n
=10m+n
所以这个两位数用含有字母的式子表示是(10m+n);原题说法错误。
说法错误的有:①②④,共3个;
故答案为:C
【点评】此题主要考查了负数的意义及其应用、用字母表示数的方法、必然事件、不可能事件、随机事件的概念以及平行线之间的距离处处相等,应灵活掌握和运用。
5.B
【分析】此题主要用正负数来表示具有意义相反的两种量:选300克为标准记为0,超过部分为正,不足的部分为负,在﹢3克和﹣3克之间的都是合格,否则,即为不合格。
【解析】300-3=297(克)
300+3=303(克)
297克≤合格产品的净含量≤303克,净含量为297克、302克、303克的是合格产品,净含量为292克、305克的是不合格产品,所以不合格产品有2盒。
故答案为:B
【点评】此题首先要知道以谁为标准,规定超出标准的为正,低于标准的为负,由此用正负数解答问题。
6.C
【分析】每个数都只有1个,所以每个数朝上的概率是一样的;奇数有1、3、5,偶数有2、4、6,都是3个,所以奇数和偶数朝上的概率也是一样的。
【解析】正方体的6个面除了数字不同,没有其他不同,每个面朝上的概率是一样的。
故答案为:C
【点评】当条件对事件的发生有利时,发生的可能性就大一些。当条件对事件的发生不利时,发生的可能性就小一些。
7.A
【分析】根据题意可知,设运来梨x千克,苹果重量比梨的2倍还多12千克,即苹果的质量×2+12千克=苹果的质量,即运来苹果(2x+12)千克,再用梨的质量+苹果的质量=运来的梨和苹果的总质量,列方程:x+(2x+12)=120,解方程,即可解答。
【解析】解:设运来梨x千克,则苹果(2x+12)千克。
x+(2x+12)=120
x+2x+12=120
3x=120-12
3x=108
x=108÷3
x=36
苹果:36×2+12
=72+12
=84(千克)
商店运来苹果和梨共120千克,苹果重量比梨的2倍还多12千克,两种水果各重梨36千克,苹果84千克。
故答案为:A
【点评】本题考查方程的实际应用,利用运来梨的质量与苹果的质量与总质量之间的关系,设出未知数,找出相关的量,列方程,解方程。
8.B
【分析】根据题意可知,设乙地开出的汽车每小时行x千米,用(甲地开出的汽车速度+乙地开出的汽车速度)×相遇时间=甲、乙两地之间的公路长度,据此列方程解答。
【解析】解:设乙地开出的汽车每小时行x千米,
(52+x)×3.5=336
(52+x)=336÷3.5
52+x=96
x=96-52
x=44
故答案为:B
【点评】本题考查相遇问题,根据题意,找出相关的量,列方程,解方程。
9.40
【分析】根据正方体的体积=棱长×棱长×棱长,代入数据求出正方体的体积,也就是长方体钢材的体积,根据长方体的体积=长×宽×高,用长方体的体积除以长,再除以宽即可求出高是多少分米,再根据1分米=10厘米,把分米化成厘米即可。
【解析】10×10×10÷25÷10
=100×10÷25÷10
=1000÷25÷10
=40÷10
=4(分米)
4分米=40厘米
所以锻造成的钢材高是40厘米。
10.4 2
【分析】
根据正方体的展开图知识,属于“1-3-2型”,折成正方体后,有公共边的两个面相邻,没有公共边的两个面相对。1号面相对的是5号面;2号面相对的是4号面,3号面相对的是6号面。
【解析】由分析可知:
如图,一个正方体的展开图,2号面相对的是4号面;4号面相对的是2号面。
11.144
【分析】设可剪成边长为2厘米的小正方形x个,则剪成边长为3厘米的小正形(x-20)个,根据边长为2厘米的小正方形的面积和等于边长为3厘米的小正方形的面积和,据此列方程解答。再用所得解乘边长为2厘米的小正方形的面积,即可得到这张纸的面积。
【解析】解:设可剪成边长为2厘米的小正方形x个,则剪成边长为3厘米的小正形(x-20)个。
(平方厘米)
原来这张正方形纸的面积是144平方厘米。
12.甲
【分析】﹣1、0、3、﹣4、6、﹣5、10这7个数中,自然数有0、3、6、10,共4个,不是自然数的有个;可能性的大小由事件出现的次数多少来决定,据此解答即可。
【解析】自然数有0、3、6、10,共4个,不是自然数的有个,摸出自然数的可能性大一些,所以甲得分的机会多。
13.3/三 讲故事
【分析】任意摸出一张,可能有3种结果即:唱歌卡片、跳舞卡片、讲故事卡片;因为讲故事卡片的个数最少,所以摸出讲故事卡片的可能性最小。
【解析】7>5>2
摸出的卡片颜色有3种可能,摸出讲故事卡片的可能性最小。
【点评】解答此题应根据题意,并根据可能性的求法,进行分析,也可以根据各种卡片的数量进行比较,即可得出结论。
14.27
【分析】根据“平行线之间的距离处处相等”,观察图形可知,三角形CDE与平行四边形ABCD等底等高;再根据“三角形的面积是与其等底等高的平行四边形面积的一半”,据此可知:已知三角形的面积,用三角形的面积乘2,即可求出与三角形等底等高的平行四边形的面积;据此解题即可。
【解析】13.5×2=27(m2)
所以平行四边形ABCD的面积是27m2。
【点评】解答此题的主要依据是:等底等高的三角形和平行四边形的面积的关系。
15.24 33
【分析】根据题意,可得到等量关系式:下层人数+上层人数=57,由此可设上层乘客数是x人,则下层乘客数是x+9人,再根据一共是57人,列出方程解答。
【解析】解:设上层乘客数是x人,则下层乘客数是x+9人
x+(x+9)=57
2x+9=57
2x=57-9
2x=48
x=48÷2
x=24
24+9=33(人)
上层有乘客24人,下层有33人。
【点评】关键是根据题意设出未知数,再找出数量关系等式,列出方程解答。
16.3
【分析】设x天后师傅比徒弟多装21台计算机,师傅每天装配12台,x天装配12x台;徒弟每天装5台,x天装5x台,师傅比徒弟多装21台计算机,即师傅装的计算机的台数-徒弟装的计算机的台数=21台,列方程:12x-5x=21,解方程,即可解答。
【解析】解:设x天后师傅比徒弟多装21台计算机。
12x-5x=21
7x=21
x=21÷7
x=3
师徒两人同时装配计算机,师傅每天装配12台,徒弟每天装5台。结果3天后师傅比徒弟多装21台计算机。
【点评】本题考查方程的实际应用。利用师傅和徒弟装计算机天数和计算机台数的关系,设出未知数,找出相关的量,列方程,解方程。
17.2 ﹣5
【分析】在数轴上,从﹣3对应的点向右数5个单位长度就是点B的位置,再从点B向左数7个单位长度就是点C的位置,写出点B、C对应的数即可。
【解析】一只小乌龟沿直线从﹣3对应的点开始向右爬行5个单位长度,到达点B,然后向左爬行7个单位长度,到达点C。那么点B对应的数是2,点C对应的数是﹣5。
【点评】本题考查正负数在数轴上的认识,根据题意数清格数即可。
18.1 3 3 5
【分析】长方体有12条棱,12条棱可以分3组:4条长,4条宽,4条高,长、宽、高分别相等。有8个顶点,每个顶点处由长、宽、高三条棱组成。据此可知,5厘米的长已经有3根,还差1根,3厘米的高有1根,还差3根,2厘米的宽有1根,还差3根,顶点已经有3个,还差5个。
【解析】4-3=1(根)
4-1=3(根)
8-3=5(个)
用磁力棒和磁力珠搭一个长方体框架,如图,已经搭了一部分,还需要5厘米的磁力棒1根,3厘米的磁力棒3根,2厘米的磁力棒3根,每个顶点一个磁力珠,还需要磁力珠5个。
【点评】本题根据长方体的特征解答。
19.6
【分析】小明同学担任领唱,位置固定,第二位同学有3个位置可以选择,第三位同学有2个位置可以选择,第四位同学有1个位置可以选择,据此利用乘法原理计算。
【解析】3×2×1=6(种)
即有6种不同的排法。
【点评】掌握在排列组合中乘法原理的应用是解答题目的关键。
20.22 4n+2
【分析】棱长为1厘米的正方体的一个面的面积是1平方厘米,且相邻的2个正方体拼组在一起减少了2个小正方体的面:
第一个长方体的表面积是:6个小正方体的面,可以写成1×4+2;
第二个长方体的表面积是:10个小正方体的面,可以写成2×4+2;
第三个长方体的表面积是:14个小正方体的面,可以写成3×4+2;
第五个长方体的表面积是:22个小正方体的面,可以写成5×4+2;
…
则第n个长方体的表面积是:4n+2个小正方体的面。
【解析】根据题干分析可得:
第五个长方体的表面积是:
5×4+2
=20+2
=22(平方厘米)
第n个长方体的表面积是:4n+2个小正方体的面。
【点评】主要考查了找规律,解答此题关键是首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。
21.√
【分析】长方体的特征:长方体有12条棱,相对的四条棱长度相等,即长、宽、高各有4条;如果长方体六个面中有两个面是正方形时,则会出现更多长度相等的棱。
【解析】在长方体的所有棱中,至少有4条棱的长度是相等的。
原题说法正确。
故答案为:√
22.√
【分析】在数轴上,到﹢3点单位长度的点分别在该点的左边和右边两种情况,据此解答。
【解析】4-3=1
4+3=7
数轴上,离开﹢3这个点4个单位长度的点所表示的数是﹣1和7。
原题干说法正确。
故答案为:√
【点评】本题主要考查对数轴的认识,解题时注意离开﹢3点单位长度的点有两种情况,不要漏解。
23.×
【分析】设扩大前正方体的棱长为a,扩大后的棱长为2a;根据正方体棱长总和公式:正方体棱长总和=棱长×12;求出扩大前正方体棱长总和和扩大后正方体棱长总和,进而解答。
【解析】设扩大前正方体棱长为a,扩大后正方体棱长为2a。
(2a×12)÷(a×12)
=24a÷12a
=2
正方体的棱长扩大2倍,它的棱长之和就扩大2倍。
原题干说法错误。
故答案为:×
【点评】熟练掌握正方体棱长总和公式是解答本题的关键。
24.×
【分析】最高气温是5℃,是一个正数。最低气温是﹣5℃,是一个负数。任何一个负数都比正数小,据此判断即可。
【解析】﹣5℃<5℃
则最低气温要小于最高气温,题干说法错误。
故答案为:×
【点评】本题考查正负数比较大小的方法。任何一个正数都比0大,任何一个负数都比0小,任何一个负数都比正数小。
25.×
【分析】硬币有两面,正面和反面。每次抛硬币,可能正面朝上,也可能反面朝上,且每次得到的结果与之前得到的结果无关,据此判断即可。
【解析】小宇抛100次硬币,正面和反面朝上的次数不一定相同,可能正面朝上的次数多,也可能反面朝上的次数多,也可能两个结果的次数相同。
故答案为:×
【点评】本题考查时间的确定性和不确定性,关键是明确每次抛硬币都是一次全新的实验,结果与之前的结果无关。
26.0.18;0.63;6.04;0.91;0.04
9.1;16;0.09;3.6;30.8
【解析】略
27.15;738;1.08
【分析】(1)运用加法交换律和加法结合律简算;
(2)运用乘法分配律简算;
(3)根据小数四则混合运算的顺序,先算除法,再算减法,接着算加法,最后算乘法。
【解析】
=(5.6+4.4)+(0.78+4.22)
=10+5
=15
=7.38×(99+1)
=7.38×100
=738
=
=
=0.9×1.2
=1.08
28.x=302;x=18;x=2;x=14
【分析】(1)根据等式的基本性质两边同时加上10,再同时除以5即可;
(2)方程左边简化为0.4+0.2x,然后根据等式的基本性质等式两边同时减去0.4,然后再同时除以0.2即可;
(3)方程左边简化为0.5x,然后根据等式的基本性质等式两边同时除以0.5即可;
(4)根据等式的基本性质等式两边同时加上2x,然后同时减去7,最后同时除以2即可。
【解析】
解:5x-10+10=1500+10
5x=1510
5x÷x=1510÷5
x=302
(2)
解:0.4+0.2x=4
0.4+0.2x-0.4=4-0.4
0.2x=3.6
0.2x÷0.2=3.6÷0.2
x=18
(3)
解:0.5x=1
0.5x÷0.5=1÷0.5
x=2
(4)
解:35-2x+2x=7+2x
7+2x=35
7+2x-7=35-7
2x=28
2x÷2=28÷2
x=14
29.156立方厘米
【分析】
如图,组合体的体积等于两个长方体的体积和,长方体体积公式:V=abh,据此分别计算出两个长方体的体积,相加即可。
【解析】V1=abh
=10×4×(6-3)
=40×3
=120(立方厘米)
V2=abh
=3×3×4
=36(立方厘米)
V=V1+V2=120+36=156(立方厘米)
这个组合体的体积是156立方厘米。
30.见详解
【分析】由图可知,每个转盘上等分了8份
(1)要使指针停在红色区域的可能性大,则涂红色的份数最多,可涂4份红色、2份黄色、2份绿色;
(2)要使指针停在绿色区域的可能性分别是红色和黄色的2倍,则可涂2份红色、2份黄色、4份绿色;
(3)要使指针停在绿色、红色、黄色区域的可能性都一样,则可涂2份红色、2份黄色、2份绿色、2份蓝色;据此涂色即可。
【解析】根据分析作图如下:
【点评】解答此题关键是根据题目要求及可能性的大小确定出各种颜色要涂几份。
31.能
【分析】设经过x分钟后爸爸追上小丁丁;根据路程=速度×时间,小丁丁每分钟60米,先求出小丁丁9分钟走的路程,列式为60×9;再求走x分钟行的路程,即60x米;爸爸骑自行车每分钟180米,x分钟爸爸行了180x米;小丁丁走的路程=爸爸骑自行车行的路程,列方程:60×9+60x=180x,解方程,求出经过多少分钟爸爸追上小丁丁,再加上9分钟,求出小丁丁走的时间;再和小丁丁上学的时间比较,如果大于小丁丁上学用的时间,爸爸不能在小丁丁到达学校前追上,如果小于小丁丁上学用的时间,爸爸能在小丁丁到达学校前追上,据此解答。
【解析】8:15-8:00=15(分钟)
解:设经过x分钟后爸爸追上小丁丁。
60×9+60x=180x
540+60x=180x
540+60x-60x=180x-60x
120x=540
120x÷120=540÷120
x=4.5
4.5+9=13.5(分钟)
13.5分钟<15分钟,爸爸能在小丁丁到达前追上他。
答:爸爸能在小丁丁到达前追上他。
32.24张;240人
【分析】根据题意,可以设学校共有张餐桌;如果每张餐桌坐12人,那么空出4张餐桌,则用餐学生共有(12-12×4)人;如果每张餐桌坐10人,那么正好坐满,则用餐学生共有10人。根据用餐学生人数不变,据此列出方程,并求解。
【解析】解:设学校共有张餐桌。
12-12×4=10
12-48=10
12=10+48
12-10=48
2=48
=48÷2
=24
10×24=240(人)
答:学校共有24张餐桌,用餐学生共有240人。
33.2分钟
【分析】设经过x分钟两人相遇;根据速度×时间=路程,用小巧的速度×2.5分钟,求出小巧2.5分钟行的路程,小巧平均每分钟行60米,x分钟行60x米;小亚每分钟行65米,x分钟行65x米,小巧现行的2.5分钟的路程+小巧x分钟行的路程+小亚x分钟行的路程=跑道一周的长度,列方程:60×2.5+60x+65x=400,解方程,即可解答。
【解析】解:设经过x分钟两人相遇。
60×2.5+60x+65x=400
150+60x+65x=400
150+125x-150=400-150
125x=250
125x÷125=250÷125
x=2
答:经过2分钟两人相遇。
34.15个;1020本
【分析】设一共有x个新书架,如果每个书架放60本,那么还缺2个书架,即每个书架放60本,需要(x+2)个书架,根据每个书架放的本数×书架个数=总本数,列出方程求出x的值是新书架个数,通过新书架个数再求出图书总本数即可。
【解析】解:设一共有x个新书架。
60×(x+2)=68x
60x+120=68x
60x+120-60x =68x-60x
8x=120
8x÷8=120÷8
x=15
68×15=1020(本)
答:一共有15个新书架,这批图书共有1020本。
35.45个;305枚
【分析】设糕点店里两种礼盒各有x个,若用6枚装的礼盒,则月饼的总个数表示为(6x+35)个;若用8枚装的礼盒,则月饼的总个数表示为(8x-55)个。根据两种包装下,月饼的总个数相等,列出方程。
【解析】解:设糕点店里两种礼盒各有x个。
6x+35=8x-55
35+55=8x-6x
90=2x
x=90÷2
x=45
6×45+35
=270+35
=305(枚)
答:糕点店里两种礼盒各有45个,这一天一共加工了305枚月饼。
【点评】此题考查了盈亏问题。在分配问题中(“盈不足问题”),因为分配的总量不变,可由不同的分配方法表示出同一种量,进而列出方程求解。
36.(1)2000立方厘米
(2)400毫升
【分析】(1)从图中可以看出,甲容器装水的体积等于甲容器体积的一半,根据长方体的体积公式V=abh,代入数据计算求解。
(2)从图中可知,甲容器的底面积是(40×10)平方厘米;将甲容器的右面作为底面,直立起来就是乙容器,则乙容器的底面积是(10×10)平方厘米;
将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,则水的体积不变,水的高度一样,那么可以把甲、乙两个容器看作一个底面积为甲、乙两个底面积之和的容器;
根据长方体的高h=V÷S,代入数据计算求出容器中水的高度;再根据长方体的体积公式V=abh,求出乙容器中水的体积。注意单位的换算:1立方厘米=1毫升。
【解析】(1)40×10×10÷2
=400×10÷2
=4000÷2
=2000(立方厘米)
答:甲容器中水的体积是2000立方厘米。
(2)2000÷(40×10+10×10)
=2000÷(400+100)
=2000÷500
=4(厘米)
10×10×4
=100×4
=400(立方厘米)
400立方厘米=400毫升
答:乙容器中需要倒入400毫升水。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
