【期末密押提分】期末全真模拟预测卷-2024-2025学年四年级下学期数学苏教版(含解析)
文档属性
| 名称 | 【期末密押提分】期末全真模拟预测卷-2024-2025学年四年级下学期数学苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 19:46:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年四年级下学期数学期末全真模拟预测卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
注意书写工整,格式正确,卷面整洁。
一.选择题(共8小题,8分)
1.下面各图中,能说明“5×3+4×3”与“(5+4)×3”相等的是( )
A. B. C.
2.一个三角形的两条边长分别是3厘米和7厘米,它的第三条边长可能是( )
A.2厘米 B.3厘米 C.7厘米
3.聪聪做了灯笼,它的底部如图。如果想再加一根木条使底部框架更牢固,下面方法中最好的是( )
A. B. C.
4.如果△×〇=36000,要使积变成360,下面的方法中,( )是不可能的。
A.△乘10,〇除以1000 B.△乘10,〇除以10 C.△和〇同时除以10
5.已知△÷〇=□,下面错误的算式是( )
A.□×〇=△ B.□÷〇=△ C.△÷□=〇
6.小强3天看完一本书,平均每天看30页.他前两天每天看的都超过了30页,那么他第三天看的页数( )
A.比30页少 B.正好30页 C.比30页多 D.无法判断
7.下面数对中表示的位置和(3,5)在同一行的是( )
A.(5,6) B.(6,3) C.(6,5)
8.把( )扩大到它的10倍,再缩小到它的得0.7069。
A.70.69 B.7.069 C.706.9 D.7069
二.填空题(共12小题,20分)
9.在横线里填“>”、“<”或“=”。
207900 207910 240×15 240×10+5 10个一千万 1亿
10.2023年5月21日,太原国际马拉松鸣枪开赛,向来自25个国家的35000名选手展示了锦绣太原城的魅力。东东和家人一起参加了亲子马拉松,他的身份证号码是1401**20130521****,他今年 周岁。
11.体育课上,四(2)班38人都在场上打乒乓球,有的是两人单打,有的是4人双打,一共用了12张乒乓球台.正在进行单打的乒乓球台有 张.
12.田庆的父母买了一套新房子,首付款四舍五入到万位后是63万元。这套房子的首付款最贵是 元,最便宜是 元。
13.三角形中有一个角是45°,如果剪去这个角(如图),剩下部分的内角和是 °。
14.用分别写有数字0、0、3、5、7的五张卡片,摆成最大的五位数是 ,和50000最接近的是 ,会读两个零的最小的是 。
15.有一个三角形,已知其中两个角分别是30°、40°,那么第三个角是 度,这是一个 三角形。
16.计算器上的数字键“8”坏了,如果想用这台计算器计算24×18,你会怎么按键?请你用算式表示出来,算式为 ,你这样想运用了哪个运算定律?
17.如图中,左边是一副三角尺中的一块,右边是一个等腰三角形,那么∠3= 度。
18.计算57×132时,如果第二个乘数减少3,那么积就减少 。
19.一个长15厘米的长方形,长增加5厘米,面积就增加15平方厘米,这个长方形原来的面积是 平方厘米。
20.一个三角形每条边的长都是整厘米数,其中两条边的长度分别是12厘米和8厘米,第三条边最长是_______ 厘米,最短是 厘米。
三.判断题(共5小题,5分)
21.“光每秒传播30万千米,多少秒能传播120万千米?”这个问题是求光的速度。
22.5□2×4□的积一定是五位数。
23.同一平面内,点A从位置(2,x)开始,沿水平方向平移一段距离,可运动到位置(2,y)。
24.五边形的内角和是5×180°=900°。
25.30□×1□的乘积可能是四位数,也可能是五位数。
四.计算题(共3小题,25分)
26.直接写得数。(共10分)
40×700= 53+28= 125×8= 540÷60= 87+43=
750÷15= 70×80= 75﹣25= 42×0+5= 9×5÷9×5=
27.列竖式计算。(共6分)
246×13= 45×302= 650×30=
28.怎样算简便就怎样算(共9分)
247+82+453 54×167+33×54 25×49×4+1
五.操作题(共1小题,6分)
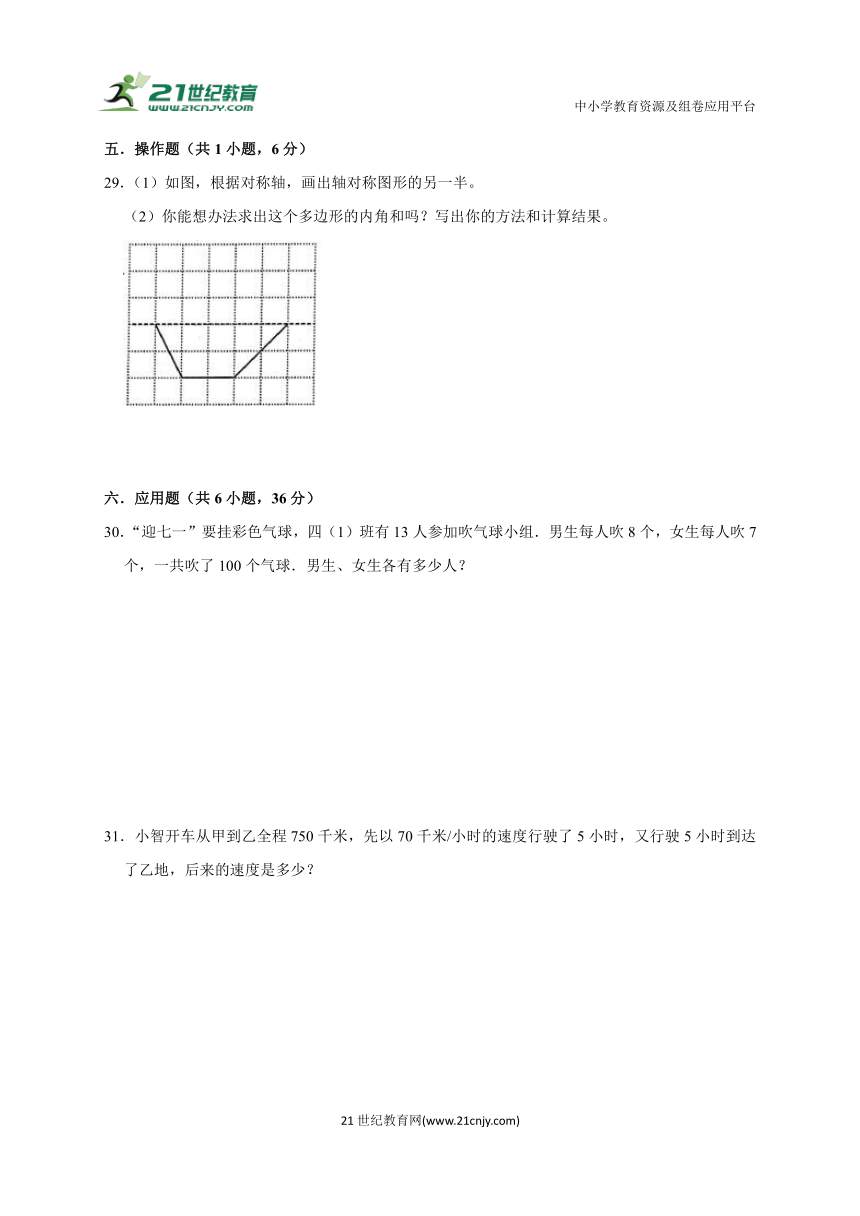
29.(1)如图,根据对称轴,画出轴对称图形的另一半。
(2)你能想办法求出这个多边形的内角和吗?写出你的方法和计算结果。
六.应用题(共6小题,36分)
30.“迎七一”要挂彩色气球,四(1)班有13人参加吹气球小组.男生每人吹8个,女生每人吹7个,一共吹了100个气球.男生、女生各有多少人?
31.小智开车从甲到乙全程750千米,先以70千米/小时的速度行驶了5小时,又行驶5小时到达了乙地,后来的速度是多少?
32.小红和小明在环形跑道上跑步,从同一点出发,背向而行,已知小红速度是2米/秒,小明的速度是3米/秒,80秒后两人相遇.这条环形跑道长多少米?
33.疫情期间“快递小哥”成为人民生活的“摆渡人”,平凡人也是真英雄。张叔叔李叔叔两位配送员同时从同一饭店出发,向相反的方向驶去。张叔叔骑行的速度是340米/分,李叔叔骑行的速度是360米/分,10分钟后他们相距多少千米?
34.甲乙两车从相距735km的两地相对而行,乙车先行3小时,甲车才出发,已知甲车每小时行70km,乙车每小时行65km,甲车开出几小时后与乙车相遇?
35.体育强国,我们每个人都要努力。小强和小军每天去学校的环形跑道上跑步,他们从同一地点同时出发,反向而行,小强的速度是4米/秒,小军的速度是6米/秒,经过40秒两人相遇。环形跑道长多少米?
参考答案与试题解析
一.选择题(共8小题,8分)
1.C
【分析】算式“5×3+4×3”表示求5个3与4个3的和,算式“(5+4)×3”表示求3个(5+4)的和。据此分析各个选项中图形的意义,看哪个图形表示的意义能说明“5×3+4×3”与“(5+4)×3”相等即可。
【解析】解:选项A,求5本笔记本和3支笔一共多少元,可以用算式5×3+3×3或(5+3)×3解答,不能说明“5×3+4×3”与“(5+4)×3”相等;
选项B,求黑色球和白色球一共有多少个,可以用算式5×4+3×4或(5+3)×4解答,不能说明“5×3+4×3”与“(5+4)×3”相等;
选项C,求黑色三角形和白色三角形一共有多少个,可以用算式5×3+5×3或(5+4)×3解答,能说明“5×3+4×3”与“(5+4)×3”相等。
故选:C。
【点评】本题考查了对算式意义的理解,准确识图是关键。
2.C
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可.
【解析】解:7﹣3<第三边<7+3,
4<第三边<10,那么第三边的长度可能是5、6、7、8、9厘米;
故选:C.
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可.
3.C
【分析】三角形具有稳定性,不易变形的特点,生活中很多设计都是运用这一特性设计的。
【解析】解:有三角形的设计,所以这种加固方法最好。
故选:C。
【点评】本题考查了三角形具有稳定性的应用。
4.B
【分析】一个因数不变,另一个因数乘几或除以几(0除外),积也乘或除以几;如果一个因数乘几,另一个因数除以相同的数(0除外),那么积不变。
【解析】解:A.因为△×〇=36000,所以
(△×10)×(〇÷1000)
=36000×10÷1000
=360
B.因为△×〇=36000,△乘10,〇除以10,所以△×〇=36000;
C.因为△×〇=36000,(△÷10)×(〇÷10)=36000÷10÷10=360;
故选:B。
【点评】熟练掌握积的变化规律是解题的关键。
5.B
【分析】根据被除数=商×除数,除数=被除数÷商即可解答。
【解析】解:已知△÷〇=□,错误的算式是□÷〇=△。
故选:B。
【点评】本题主要考查被除数=商×除数,除数=被除数÷商。
6.A
【分析】首先根据平均数的含义和求法,用小强平均每天看的书的页数乘3,求出这本书一共有多少页;然后用它减去前两天看的页数,求出他第三天看的页数和30的关系即可.
【解析】解:30×3﹣30×2
=90﹣60
=30(页)
因为他前两天每天看的都超过了30页,
所以他第三天看的页数比30页少.
答:他第三天看的页数比30页少.
故选:A.
【点评】此题主要考查了乘法、减法的意义的应用,要熟练掌握,解答此题的关键是求出这本书一共有多少页.
7.C
【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,用数对表示的两个点的位置时,第一个数字相同,这两点在同一列,第二个数字相同时,这两点在同一行。
【解析】解:与数对(3,5)在同一行的位置是(6,5)。
故选:C。
【点评】数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行。
8.A
【分析】把一个小数先扩大到它的10倍,即小数点向右移动1位,再缩小到所得数的,即小数点向左移动3位,这个小数的小数点应向左移动2位得到0.7069,据此解答。
【解析】解:把70.69扩大到它的10倍,再缩小到它的得0.7069。
故选:A。
【点评】此题主要考查小数点位置移动引起数的大小变化规律,要熟练掌握。
二.填空题(共12小题,20分)
9.<;>;=。
【分析】根据整数的简单运算和比较大小即可解答。
【解析】解:
207900<207910 240×15>240×10+5 10个一千万=1亿
故答案为:<;>;=。
【点评】本题主要考查整数的比较大小。
10.见试题解答内容
【分析】身份证上第7~14位表示出生日期,用今年(2023年)减去他出生的年份即可。
【解析】解:2023﹣2013=10(周岁)
答:他今年10周岁。
故答案为:10。
【点评】本题是考查了身份证的数字编码问题,身份证上:
前六位是地区代码;
7~14位是出生日期;
15~17位是顺序码,其中第17位奇数分给男性,偶数分给女性;
第18位是校验码。
11.5。
【分析】假设都是单打,则人数为:12×2=24(人),比实际少:38﹣24=14(人),每桌双打与单打相差4﹣2=2(人),所以双打的有14÷2=7(张),单打为12﹣7=5(张)。据此解答。
【解析】解:(38﹣2×12)÷(4﹣2)
=14÷2
=7(张)
12﹣7=5(张)
答:正在进行单打的乒乓球台有5张。
故答案为:5。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
12.634999,625000。
【分析】一个数省略万位后面的尾数是63万,最大是千位上的数舍去得到的,舍去的数中4是最大的,其它数位百位、十位、个位是最大的一位数9即可;最小是千位上的数进一得到的,进一的数中5是最小的,其它数位百位、十位、个位是最小的自然数0即可。
【解析】解:一个数省略万位后面的尾数是63万,这个数最大是634999,最小是625000。
故答案为:634999,625000。
【点评】本题主要考查近似数的求法,注意最大是千位上的数舍去得到的,最小是千位上的数进一得到的。
13.360。
【分析】剪去这个角后,变成一个四边形,四边形的内角和是360°。
【解析】解:三角形中有一个角是45°,如果剪去这个角(如图),剩下部分的内角和是360°。
故答案为:360。
【点评】四边形的内角和是360°。
14.75300,50037,30507。
【分析】要想组成的数最大,要把数字按照从大到小的顺序从高位到低位排下来;
最接近50000的数就是用五个数字组成的与50000差最小的数;
要想组成的数最小,要把数字按照从小到大的顺序从高位到低位排下来,但是最高位不能是零,据此写出会读两个零的数。
【解析】解:最大的五位数是75300;
与50000最接近的数是50037;
会读两个零的最小的是30507。
故答案为:75300,50037,30507。
【点评】本题是考查整数的读、写法,分级读、写或借助数位表读、写数能较好的避免读、写错数的情况,是常用的方法,要熟练掌握。
15.110;钝角。
【分析】因为三角形的内角度数和是180°,所以第三个角是:180°﹣30°﹣40°;找出最大的角的度数,然后根据三角形的分类判定类型即可。
【解析】解:第三个角是:
180°﹣30°﹣40°
=150°﹣40°
=110°
三角形中的三个角分别是:30°、40°、110°,最大角是110°是钝角,所以三角形是钝角三角形。
故答案为:110;钝角。
【点评】解答此题应明确三角形的内角度数的和是180°,求出最大的角的度数,然后根据三角形的分类判定类型。
16.24×(17+1);乘法分配律。
【分析】用计算器计算24×18,可是计算器上的按键“8”坏了,可以将18拆成(17+1),算式变为24×(17+1),然后再按照乘法分配律计算。
【解析】解:计算器上的数字键“8”坏了,如果想用这台计算器计算24×18,你会怎么按键?请你用算式表示出来,算式为:24×(17+1),你这样想运用了哪个运算定律?乘法分配律。
故答案为:24×(17+1);乘法分配律。
【点评】当计算器中数字键坏了后,可以运用加减乘除法将不能按出的数字转换成别的算式,再进行解答。
17.30。
【分析】根据左边是一副三角尺中的一块,并且不是等腰直角三角形的那一块,所以较小的那个角是30°,另一个角是60°,还有一个直角。60°的角与右边等腰三角形的顶角和是180°,再根据三角形的内角和是180°,所以可以算出两个底角的和,再根据等腰三角形的特征,两个底角度数相等,即可得解。
【解析】解:180°﹣(180°﹣60°)=60°
60°÷2=30°
所以∠3=30°。
故答案为:30。
【点评】此题考查了对三角形内角和的灵活应用。
18.171。
【分析】先用132减去3,计算出第二个乘数减少3后是129,然后分别计算出57×132和57×129的结果,再求出积减少的数。
【解析】解:132﹣3=129
57×132=7524
57×129=7353
7524﹣7353=171
答:积就减少171。
故答案为:171。
【点评】本题解题的关键是熟练掌握两位数乘三位数的计算方法。
19.45。
【分析】先求出原来长方形的宽,再根据长方形的面积=长×宽,求出面积即可。
【解析】解:15÷5=3(厘米)
15×3=45(平方厘米)
答:这个长方形原来的面积是45平方厘米。
故答案为:45。
【点评】熟练掌握长方形的面积公式,是解答此题的关键。
20.19,5。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解析】解:12+8=20(厘米)
最长:20﹣1=19(厘米)
12﹣8=4(厘米)
最短:4+1=5(厘米)
答:第三条边最长是19厘米,最短是5厘米。
故答案为:19,5。
【点评】本题考查了三角形的三边关系的应用。
三.判断题(共5小题,5分)
21.×
【分析】根据题意,光每秒传播30万千米是光的传播速度,传播120万千米是光传播的路程,这个问题是已知速度和路程,求光的传播时间。
【解析】解:“光每秒传播30万千米,多少秒能传播120万千米?”这个问题是求光的传播时间,
所以题中说法不正确。
故答案为:×。
【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
22.√
【分析】可以把□中的数看作0(最小)或9(最大)计算出结果,再进行判定。
【解析】解:502×40=20080
592×49=29008
积都是五位数,所以原题干说法正确。
故答案为:√。
【点评】本题主要考查了两位数乘三位数乘法的计算。
23.×
【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,数对(2,x)与数对(2,y)表示的位置在同一列,根据此判断即可。
【解析】解:同一平面内,点A从位置(2,x)开始,沿水平方向平移一段距离,可运动到位置(2,y)是错误的,因为不在一列。
故答案为:×。
【点评】此题考查了数对表示位置的方法的应用。
24.×
【分析】根据多边形内角和定理:n边形的内角的和等于:(n﹣2)×180°(n大于等于3)。
【解析】解:(5﹣2)×180°
=3×10°
=540°
答:五边形的内角和是(5﹣2)×180°,不是5×180°=900°。所有原题说法错误。
故答案为:×。
【点评】解答本题的关键是熟练掌握多边形内角和定理n边形的内角的和定理。
25.×
【分析】可以把□中的数看成0或9进行计算,再进一步解答。
【解析】解:300×10=3000,积是四位数;
309×19=5871,积是四位数。
所以30□×1□的乘积是四位数,原题干说法错误。
故答案为:×。
【点评】本题主要考查了两位数乘三位数乘法的运算,用赋值法更能直观的进行说明。
四.计算题(共3小题,25分)
26.28000;81;1000;9;130;50;5600;50;5;25。
【分析】根据整数加减乘除的计算方法,依次口算结果。
【解析】解:
40×700=28000 53+28=81 125×8=1000 540÷60=9 87+43=130
750÷15=50 70×80=5600 75﹣25=50 42×0+5=5 9×5÷9×5=25
【点评】本题解题的关键是熟练掌握整数加减乘除的计算方法。
27.3198,13590,19500。
【分析】根据两位数乘三位数乘法的竖式计算方法进行解答即可。
【解析】解:246×13=3198
45×302=13590
650×30=19500
【点评】本题主要考查了两位数乘三位数乘法的竖式计算方法,注意计算的准确性。
28.782,10800,4901。
【分析】(1)用加法交换律计算。
(2)用乘法分配律计算。
(3)用乘法交换律计算。
【解析】解:(1)247+82+453
=247+453+82
=700+82
=782
(2)54×167+33×54
=54×(167+33)
=54×200
=10800
(3)25×49×4+1
=25×4×49+1
=100×49+1
=4900+1
=4901
【点评】本题考查了整数的四则运算,灵活使用运算律可使计算简便。
五.操作题(共1小题,6分)
29.(1)如图:
(2)720°
【分析】(1)从与对称轴平行的边的两个顶点分别向对称轴引垂线,并延长垂线,使从垂足到延长线上的一点间的距离等于平行线顶点到垂足的距离,然后顺次连接端点。
(2)将多边形的相对顶点连接起来,把多边形分成了4个三角形,由三角形内角和求出多边形的内角和。
【解析】解:(1)如图:
(2)如图:
多边形ABDEFC的内角和=△ABC的内角和+△BCF的内角和+△BEF的内角和+△BED的内角和
=180×4
=720°
答:多边形的内角和是720°。
【点评】本题考查了学生动手操作能力及用已有知识解决新问题的创新能力。
六.应用题(共6小题,36分)
30.9;4。
【分析】假设都是男生,则应该吹13×8=104(个)气球,比实际多104﹣100=4(个);每个男生与每个女生相差8﹣7=1(个),所以女生人数为:4÷1=4(人)。进而求出男生人数即可。
【解析】解:(13×8﹣100)÷(8﹣7)
=(104﹣100)÷1
=4÷1
=4(人)
13﹣4=9(人)
答:男生有9人,女生有4人。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
31.80千米/时。
【分析】根据路程=速度×时间,计算出5小时行的路程,再用甲到乙全程减去已行的路程,计算出未行的路程,最后根据速度=路程÷时间,计算出后来的速度是多少。
【解析】解:(750﹣70×5)÷5
=(750﹣350)÷5
=400÷5
=80(千米/时)
答:后来的速度是80千米/时。
【点评】本题解题关键是根据路程=速度×时间,计算出已行的路程,再用减法计算出未行的路程,最后根据速度=路程÷时间,列式计算。
32.400米。
【分析】相遇时两人行的路程和就是这条环形跑道的长度,根据相遇问题的数量关系式:(小红速度+小明速度)×相遇时间=路程,可以计算出这条环形跑道长多少米。
【解析】解:(2+3)×80
=5×80
=400(米)
答:这条环形跑道长400米。
【点评】本题考查行程问题的解题方法,解题关键是掌握行程问题的数量关系,利用速度和×相遇时间=路程,列式计算。
33.7千米。
【分析】根据路程、速度和时间的关系式分别求出二人骑行的路程,求和即可。
【解析】解:340×10+360×10
=3400+3600
=7000(米)
7000米=7千米
答:10分钟后他们相距7千米。
【点评】本题属于行程问题中的相离问题,也可以根据间隔距离=速度和×时间解答。
34.4。
【分析】根据题意,先计算乙车行驶3小时后两车相距的路程,然后利用相遇问题公式:相遇时间=路程和÷速度和,计算相遇时间即可。
【解析】解:(735﹣65×3)÷(70+65)
=(735﹣195)÷135
=540÷135
=4(小时)
答:甲车开出4小时后与乙车相遇。
【点评】本题主要考查简单的行程问题,关键利用路程、速度和时间的关系做题。
35.400米。
【分析】首先用小强跑步的速度加上小军跑步的速度,求出两人的速度之和是多少;然后根据速度×时间=路程,用两人的速度之和乘两人相遇用的时间,求出跑道长多少米即可。
【解析】解:(4+6)×40
=10×40
=400(米)
答:环形跑道长400米。
【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握,解答此题的关键是求出两人的速度之和是多少。
21世纪教育网(www.21cnjy.com)
2024-2025学年四年级下学期数学期末全真模拟预测卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
注意书写工整,格式正确,卷面整洁。
一.选择题(共8小题,8分)
1.下面各图中,能说明“5×3+4×3”与“(5+4)×3”相等的是( )
A. B. C.
2.一个三角形的两条边长分别是3厘米和7厘米,它的第三条边长可能是( )
A.2厘米 B.3厘米 C.7厘米
3.聪聪做了灯笼,它的底部如图。如果想再加一根木条使底部框架更牢固,下面方法中最好的是( )
A. B. C.
4.如果△×〇=36000,要使积变成360,下面的方法中,( )是不可能的。
A.△乘10,〇除以1000 B.△乘10,〇除以10 C.△和〇同时除以10
5.已知△÷〇=□,下面错误的算式是( )
A.□×〇=△ B.□÷〇=△ C.△÷□=〇
6.小强3天看完一本书,平均每天看30页.他前两天每天看的都超过了30页,那么他第三天看的页数( )
A.比30页少 B.正好30页 C.比30页多 D.无法判断
7.下面数对中表示的位置和(3,5)在同一行的是( )
A.(5,6) B.(6,3) C.(6,5)
8.把( )扩大到它的10倍,再缩小到它的得0.7069。
A.70.69 B.7.069 C.706.9 D.7069
二.填空题(共12小题,20分)
9.在横线里填“>”、“<”或“=”。
207900 207910 240×15 240×10+5 10个一千万 1亿
10.2023年5月21日,太原国际马拉松鸣枪开赛,向来自25个国家的35000名选手展示了锦绣太原城的魅力。东东和家人一起参加了亲子马拉松,他的身份证号码是1401**20130521****,他今年 周岁。
11.体育课上,四(2)班38人都在场上打乒乓球,有的是两人单打,有的是4人双打,一共用了12张乒乓球台.正在进行单打的乒乓球台有 张.
12.田庆的父母买了一套新房子,首付款四舍五入到万位后是63万元。这套房子的首付款最贵是 元,最便宜是 元。
13.三角形中有一个角是45°,如果剪去这个角(如图),剩下部分的内角和是 °。
14.用分别写有数字0、0、3、5、7的五张卡片,摆成最大的五位数是 ,和50000最接近的是 ,会读两个零的最小的是 。
15.有一个三角形,已知其中两个角分别是30°、40°,那么第三个角是 度,这是一个 三角形。
16.计算器上的数字键“8”坏了,如果想用这台计算器计算24×18,你会怎么按键?请你用算式表示出来,算式为 ,你这样想运用了哪个运算定律?
17.如图中,左边是一副三角尺中的一块,右边是一个等腰三角形,那么∠3= 度。
18.计算57×132时,如果第二个乘数减少3,那么积就减少 。
19.一个长15厘米的长方形,长增加5厘米,面积就增加15平方厘米,这个长方形原来的面积是 平方厘米。
20.一个三角形每条边的长都是整厘米数,其中两条边的长度分别是12厘米和8厘米,第三条边最长是_______ 厘米,最短是 厘米。
三.判断题(共5小题,5分)
21.“光每秒传播30万千米,多少秒能传播120万千米?”这个问题是求光的速度。
22.5□2×4□的积一定是五位数。
23.同一平面内,点A从位置(2,x)开始,沿水平方向平移一段距离,可运动到位置(2,y)。
24.五边形的内角和是5×180°=900°。
25.30□×1□的乘积可能是四位数,也可能是五位数。
四.计算题(共3小题,25分)
26.直接写得数。(共10分)
40×700= 53+28= 125×8= 540÷60= 87+43=
750÷15= 70×80= 75﹣25= 42×0+5= 9×5÷9×5=
27.列竖式计算。(共6分)
246×13= 45×302= 650×30=
28.怎样算简便就怎样算(共9分)
247+82+453 54×167+33×54 25×49×4+1
五.操作题(共1小题,6分)
29.(1)如图,根据对称轴,画出轴对称图形的另一半。
(2)你能想办法求出这个多边形的内角和吗?写出你的方法和计算结果。
六.应用题(共6小题,36分)
30.“迎七一”要挂彩色气球,四(1)班有13人参加吹气球小组.男生每人吹8个,女生每人吹7个,一共吹了100个气球.男生、女生各有多少人?
31.小智开车从甲到乙全程750千米,先以70千米/小时的速度行驶了5小时,又行驶5小时到达了乙地,后来的速度是多少?
32.小红和小明在环形跑道上跑步,从同一点出发,背向而行,已知小红速度是2米/秒,小明的速度是3米/秒,80秒后两人相遇.这条环形跑道长多少米?
33.疫情期间“快递小哥”成为人民生活的“摆渡人”,平凡人也是真英雄。张叔叔李叔叔两位配送员同时从同一饭店出发,向相反的方向驶去。张叔叔骑行的速度是340米/分,李叔叔骑行的速度是360米/分,10分钟后他们相距多少千米?
34.甲乙两车从相距735km的两地相对而行,乙车先行3小时,甲车才出发,已知甲车每小时行70km,乙车每小时行65km,甲车开出几小时后与乙车相遇?
35.体育强国,我们每个人都要努力。小强和小军每天去学校的环形跑道上跑步,他们从同一地点同时出发,反向而行,小强的速度是4米/秒,小军的速度是6米/秒,经过40秒两人相遇。环形跑道长多少米?
参考答案与试题解析
一.选择题(共8小题,8分)
1.C
【分析】算式“5×3+4×3”表示求5个3与4个3的和,算式“(5+4)×3”表示求3个(5+4)的和。据此分析各个选项中图形的意义,看哪个图形表示的意义能说明“5×3+4×3”与“(5+4)×3”相等即可。
【解析】解:选项A,求5本笔记本和3支笔一共多少元,可以用算式5×3+3×3或(5+3)×3解答,不能说明“5×3+4×3”与“(5+4)×3”相等;
选项B,求黑色球和白色球一共有多少个,可以用算式5×4+3×4或(5+3)×4解答,不能说明“5×3+4×3”与“(5+4)×3”相等;
选项C,求黑色三角形和白色三角形一共有多少个,可以用算式5×3+5×3或(5+4)×3解答,能说明“5×3+4×3”与“(5+4)×3”相等。
故选:C。
【点评】本题考查了对算式意义的理解,准确识图是关键。
2.C
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可.
【解析】解:7﹣3<第三边<7+3,
4<第三边<10,那么第三边的长度可能是5、6、7、8、9厘米;
故选:C.
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可.
3.C
【分析】三角形具有稳定性,不易变形的特点,生活中很多设计都是运用这一特性设计的。
【解析】解:有三角形的设计,所以这种加固方法最好。
故选:C。
【点评】本题考查了三角形具有稳定性的应用。
4.B
【分析】一个因数不变,另一个因数乘几或除以几(0除外),积也乘或除以几;如果一个因数乘几,另一个因数除以相同的数(0除外),那么积不变。
【解析】解:A.因为△×〇=36000,所以
(△×10)×(〇÷1000)
=36000×10÷1000
=360
B.因为△×〇=36000,△乘10,〇除以10,所以△×〇=36000;
C.因为△×〇=36000,(△÷10)×(〇÷10)=36000÷10÷10=360;
故选:B。
【点评】熟练掌握积的变化规律是解题的关键。
5.B
【分析】根据被除数=商×除数,除数=被除数÷商即可解答。
【解析】解:已知△÷〇=□,错误的算式是□÷〇=△。
故选:B。
【点评】本题主要考查被除数=商×除数,除数=被除数÷商。
6.A
【分析】首先根据平均数的含义和求法,用小强平均每天看的书的页数乘3,求出这本书一共有多少页;然后用它减去前两天看的页数,求出他第三天看的页数和30的关系即可.
【解析】解:30×3﹣30×2
=90﹣60
=30(页)
因为他前两天每天看的都超过了30页,
所以他第三天看的页数比30页少.
答:他第三天看的页数比30页少.
故选:A.
【点评】此题主要考查了乘法、减法的意义的应用,要熟练掌握,解答此题的关键是求出这本书一共有多少页.
7.C
【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,用数对表示的两个点的位置时,第一个数字相同,这两点在同一列,第二个数字相同时,这两点在同一行。
【解析】解:与数对(3,5)在同一行的位置是(6,5)。
故选:C。
【点评】数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行。
8.A
【分析】把一个小数先扩大到它的10倍,即小数点向右移动1位,再缩小到所得数的,即小数点向左移动3位,这个小数的小数点应向左移动2位得到0.7069,据此解答。
【解析】解:把70.69扩大到它的10倍,再缩小到它的得0.7069。
故选:A。
【点评】此题主要考查小数点位置移动引起数的大小变化规律,要熟练掌握。
二.填空题(共12小题,20分)
9.<;>;=。
【分析】根据整数的简单运算和比较大小即可解答。
【解析】解:
207900<207910 240×15>240×10+5 10个一千万=1亿
故答案为:<;>;=。
【点评】本题主要考查整数的比较大小。
10.见试题解答内容
【分析】身份证上第7~14位表示出生日期,用今年(2023年)减去他出生的年份即可。
【解析】解:2023﹣2013=10(周岁)
答:他今年10周岁。
故答案为:10。
【点评】本题是考查了身份证的数字编码问题,身份证上:
前六位是地区代码;
7~14位是出生日期;
15~17位是顺序码,其中第17位奇数分给男性,偶数分给女性;
第18位是校验码。
11.5。
【分析】假设都是单打,则人数为:12×2=24(人),比实际少:38﹣24=14(人),每桌双打与单打相差4﹣2=2(人),所以双打的有14÷2=7(张),单打为12﹣7=5(张)。据此解答。
【解析】解:(38﹣2×12)÷(4﹣2)
=14÷2
=7(张)
12﹣7=5(张)
答:正在进行单打的乒乓球台有5张。
故答案为:5。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
12.634999,625000。
【分析】一个数省略万位后面的尾数是63万,最大是千位上的数舍去得到的,舍去的数中4是最大的,其它数位百位、十位、个位是最大的一位数9即可;最小是千位上的数进一得到的,进一的数中5是最小的,其它数位百位、十位、个位是最小的自然数0即可。
【解析】解:一个数省略万位后面的尾数是63万,这个数最大是634999,最小是625000。
故答案为:634999,625000。
【点评】本题主要考查近似数的求法,注意最大是千位上的数舍去得到的,最小是千位上的数进一得到的。
13.360。
【分析】剪去这个角后,变成一个四边形,四边形的内角和是360°。
【解析】解:三角形中有一个角是45°,如果剪去这个角(如图),剩下部分的内角和是360°。
故答案为:360。
【点评】四边形的内角和是360°。
14.75300,50037,30507。
【分析】要想组成的数最大,要把数字按照从大到小的顺序从高位到低位排下来;
最接近50000的数就是用五个数字组成的与50000差最小的数;
要想组成的数最小,要把数字按照从小到大的顺序从高位到低位排下来,但是最高位不能是零,据此写出会读两个零的数。
【解析】解:最大的五位数是75300;
与50000最接近的数是50037;
会读两个零的最小的是30507。
故答案为:75300,50037,30507。
【点评】本题是考查整数的读、写法,分级读、写或借助数位表读、写数能较好的避免读、写错数的情况,是常用的方法,要熟练掌握。
15.110;钝角。
【分析】因为三角形的内角度数和是180°,所以第三个角是:180°﹣30°﹣40°;找出最大的角的度数,然后根据三角形的分类判定类型即可。
【解析】解:第三个角是:
180°﹣30°﹣40°
=150°﹣40°
=110°
三角形中的三个角分别是:30°、40°、110°,最大角是110°是钝角,所以三角形是钝角三角形。
故答案为:110;钝角。
【点评】解答此题应明确三角形的内角度数的和是180°,求出最大的角的度数,然后根据三角形的分类判定类型。
16.24×(17+1);乘法分配律。
【分析】用计算器计算24×18,可是计算器上的按键“8”坏了,可以将18拆成(17+1),算式变为24×(17+1),然后再按照乘法分配律计算。
【解析】解:计算器上的数字键“8”坏了,如果想用这台计算器计算24×18,你会怎么按键?请你用算式表示出来,算式为:24×(17+1),你这样想运用了哪个运算定律?乘法分配律。
故答案为:24×(17+1);乘法分配律。
【点评】当计算器中数字键坏了后,可以运用加减乘除法将不能按出的数字转换成别的算式,再进行解答。
17.30。
【分析】根据左边是一副三角尺中的一块,并且不是等腰直角三角形的那一块,所以较小的那个角是30°,另一个角是60°,还有一个直角。60°的角与右边等腰三角形的顶角和是180°,再根据三角形的内角和是180°,所以可以算出两个底角的和,再根据等腰三角形的特征,两个底角度数相等,即可得解。
【解析】解:180°﹣(180°﹣60°)=60°
60°÷2=30°
所以∠3=30°。
故答案为:30。
【点评】此题考查了对三角形内角和的灵活应用。
18.171。
【分析】先用132减去3,计算出第二个乘数减少3后是129,然后分别计算出57×132和57×129的结果,再求出积减少的数。
【解析】解:132﹣3=129
57×132=7524
57×129=7353
7524﹣7353=171
答:积就减少171。
故答案为:171。
【点评】本题解题的关键是熟练掌握两位数乘三位数的计算方法。
19.45。
【分析】先求出原来长方形的宽,再根据长方形的面积=长×宽,求出面积即可。
【解析】解:15÷5=3(厘米)
15×3=45(平方厘米)
答:这个长方形原来的面积是45平方厘米。
故答案为:45。
【点评】熟练掌握长方形的面积公式,是解答此题的关键。
20.19,5。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解析】解:12+8=20(厘米)
最长:20﹣1=19(厘米)
12﹣8=4(厘米)
最短:4+1=5(厘米)
答:第三条边最长是19厘米,最短是5厘米。
故答案为:19,5。
【点评】本题考查了三角形的三边关系的应用。
三.判断题(共5小题,5分)
21.×
【分析】根据题意,光每秒传播30万千米是光的传播速度,传播120万千米是光传播的路程,这个问题是已知速度和路程,求光的传播时间。
【解析】解:“光每秒传播30万千米,多少秒能传播120万千米?”这个问题是求光的传播时间,
所以题中说法不正确。
故答案为:×。
【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
22.√
【分析】可以把□中的数看作0(最小)或9(最大)计算出结果,再进行判定。
【解析】解:502×40=20080
592×49=29008
积都是五位数,所以原题干说法正确。
故答案为:√。
【点评】本题主要考查了两位数乘三位数乘法的计算。
23.×
【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,数对(2,x)与数对(2,y)表示的位置在同一列,根据此判断即可。
【解析】解:同一平面内,点A从位置(2,x)开始,沿水平方向平移一段距离,可运动到位置(2,y)是错误的,因为不在一列。
故答案为:×。
【点评】此题考查了数对表示位置的方法的应用。
24.×
【分析】根据多边形内角和定理:n边形的内角的和等于:(n﹣2)×180°(n大于等于3)。
【解析】解:(5﹣2)×180°
=3×10°
=540°
答:五边形的内角和是(5﹣2)×180°,不是5×180°=900°。所有原题说法错误。
故答案为:×。
【点评】解答本题的关键是熟练掌握多边形内角和定理n边形的内角的和定理。
25.×
【分析】可以把□中的数看成0或9进行计算,再进一步解答。
【解析】解:300×10=3000,积是四位数;
309×19=5871,积是四位数。
所以30□×1□的乘积是四位数,原题干说法错误。
故答案为:×。
【点评】本题主要考查了两位数乘三位数乘法的运算,用赋值法更能直观的进行说明。
四.计算题(共3小题,25分)
26.28000;81;1000;9;130;50;5600;50;5;25。
【分析】根据整数加减乘除的计算方法,依次口算结果。
【解析】解:
40×700=28000 53+28=81 125×8=1000 540÷60=9 87+43=130
750÷15=50 70×80=5600 75﹣25=50 42×0+5=5 9×5÷9×5=25
【点评】本题解题的关键是熟练掌握整数加减乘除的计算方法。
27.3198,13590,19500。
【分析】根据两位数乘三位数乘法的竖式计算方法进行解答即可。
【解析】解:246×13=3198
45×302=13590
650×30=19500
【点评】本题主要考查了两位数乘三位数乘法的竖式计算方法,注意计算的准确性。
28.782,10800,4901。
【分析】(1)用加法交换律计算。
(2)用乘法分配律计算。
(3)用乘法交换律计算。
【解析】解:(1)247+82+453
=247+453+82
=700+82
=782
(2)54×167+33×54
=54×(167+33)
=54×200
=10800
(3)25×49×4+1
=25×4×49+1
=100×49+1
=4900+1
=4901
【点评】本题考查了整数的四则运算,灵活使用运算律可使计算简便。
五.操作题(共1小题,6分)
29.(1)如图:
(2)720°
【分析】(1)从与对称轴平行的边的两个顶点分别向对称轴引垂线,并延长垂线,使从垂足到延长线上的一点间的距离等于平行线顶点到垂足的距离,然后顺次连接端点。
(2)将多边形的相对顶点连接起来,把多边形分成了4个三角形,由三角形内角和求出多边形的内角和。
【解析】解:(1)如图:
(2)如图:
多边形ABDEFC的内角和=△ABC的内角和+△BCF的内角和+△BEF的内角和+△BED的内角和
=180×4
=720°
答:多边形的内角和是720°。
【点评】本题考查了学生动手操作能力及用已有知识解决新问题的创新能力。
六.应用题(共6小题,36分)
30.9;4。
【分析】假设都是男生,则应该吹13×8=104(个)气球,比实际多104﹣100=4(个);每个男生与每个女生相差8﹣7=1(个),所以女生人数为:4÷1=4(人)。进而求出男生人数即可。
【解析】解:(13×8﹣100)÷(8﹣7)
=(104﹣100)÷1
=4÷1
=4(人)
13﹣4=9(人)
答:男生有9人,女生有4人。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
31.80千米/时。
【分析】根据路程=速度×时间,计算出5小时行的路程,再用甲到乙全程减去已行的路程,计算出未行的路程,最后根据速度=路程÷时间,计算出后来的速度是多少。
【解析】解:(750﹣70×5)÷5
=(750﹣350)÷5
=400÷5
=80(千米/时)
答:后来的速度是80千米/时。
【点评】本题解题关键是根据路程=速度×时间,计算出已行的路程,再用减法计算出未行的路程,最后根据速度=路程÷时间,列式计算。
32.400米。
【分析】相遇时两人行的路程和就是这条环形跑道的长度,根据相遇问题的数量关系式:(小红速度+小明速度)×相遇时间=路程,可以计算出这条环形跑道长多少米。
【解析】解:(2+3)×80
=5×80
=400(米)
答:这条环形跑道长400米。
【点评】本题考查行程问题的解题方法,解题关键是掌握行程问题的数量关系,利用速度和×相遇时间=路程,列式计算。
33.7千米。
【分析】根据路程、速度和时间的关系式分别求出二人骑行的路程,求和即可。
【解析】解:340×10+360×10
=3400+3600
=7000(米)
7000米=7千米
答:10分钟后他们相距7千米。
【点评】本题属于行程问题中的相离问题,也可以根据间隔距离=速度和×时间解答。
34.4。
【分析】根据题意,先计算乙车行驶3小时后两车相距的路程,然后利用相遇问题公式:相遇时间=路程和÷速度和,计算相遇时间即可。
【解析】解:(735﹣65×3)÷(70+65)
=(735﹣195)÷135
=540÷135
=4(小时)
答:甲车开出4小时后与乙车相遇。
【点评】本题主要考查简单的行程问题,关键利用路程、速度和时间的关系做题。
35.400米。
【分析】首先用小强跑步的速度加上小军跑步的速度,求出两人的速度之和是多少;然后根据速度×时间=路程,用两人的速度之和乘两人相遇用的时间,求出跑道长多少米即可。
【解析】解:(4+6)×40
=10×40
=400(米)
答:环形跑道长400米。
【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握,解答此题的关键是求出两人的速度之和是多少。
21世纪教育网(www.21cnjy.com)
同课章节目录
