3.1 重力与弹力 第二课时(教学课件)(共42张PPT)-高中物理人教版(2019)必修第一册
文档属性
| 名称 | 3.1 重力与弹力 第二课时(教学课件)(共42张PPT)-高中物理人教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 12.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-16 17:32:29 | ||
图片预览








文档简介
(共42张PPT)
1. 重力与弹力 第二课时
人教版(2019)物理(必修第一册)
第三章 相互作用——力
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
正确教育
素养目标
1.知道重力产生的原因,理解重力的大小及方向,知道重心的概念
2.知道力的三要素,会用力的图示和示意图来表示力
3.知道弹力产生的原因和条件,会分析弹力的方向
4.能通过实验探究弹力的大小与形变量的关系
5.能根据数据表格绘制F-x图像,求出弹簧的劲度系数
6.知道胡克定律的内容及公式
经典回顾:2008北京奥运会——跳水女子3米板 郭晶晶夺得金牌
跳水板产生了明显的形变,这其中蕴含着怎样的物理知识呢?
正确教育
弹力
弹力
被拉长的弹簧,要恢复原状,对相连接的小车产生了拉力F;
F
被跳水运动员压弯的跳板,要恢复原状,对上面的人产生了支持力。
(1)定义:发生形变的物体,由于要恢复原状对跟它接触的物体产生力的作用,这种力叫弹力。
(2)产生条件:①直接接触;②发生弹性形变
F1
放在桌面上的书,它对桌面的压力F1以及桌面对它的支持力F2,都是弹力,其方向是跟接触面垂直指向被压或被支持的物体。
F2
弹力
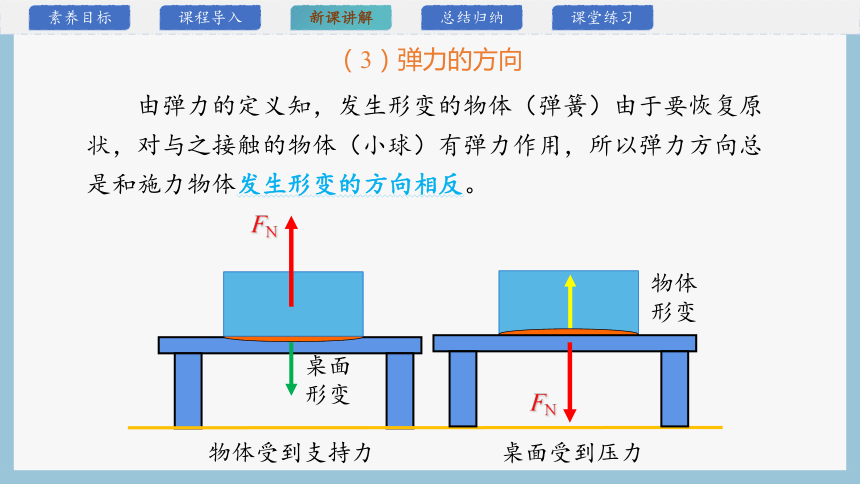
由弹力的定义知,发生形变的物体(弹簧)由于要恢复原状,对与之接触的物体(小球)有弹力作用,所以弹力方向总是和施力物体发生形变的方向相反。
(3)弹力的方向
桌面形变
FN
物体形变
FN
物体受到支持力
桌面受到压力
1.有明显形变的情况下,根据物体的形变方向来判断:弹力的方向与物体形变的方向相反.如弹簧伸长时与伸长的方向相反,压缩时与压缩的方向相反.
2.发生微小形变时,形变方向不易观察,应根据物体间接触面特点进行分析:
①面面接触,弹力垂直于公共接触面
②点面接触,弹力过点垂直于接触面
③点点接触,弹力垂直于公切面
弹力方向的判断
面面接触
A
FA
β
FB
B
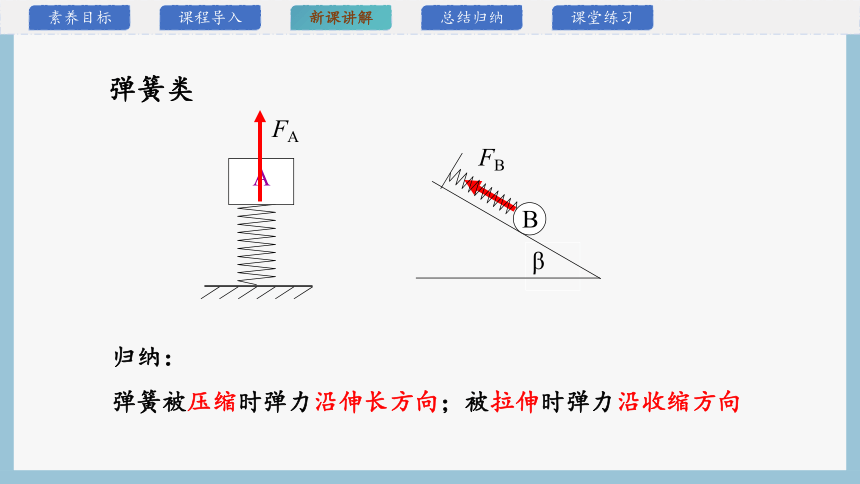
归纳:
弹簧被压缩时弹力沿伸长方向;被拉伸时弹力沿收缩方向
弹簧类
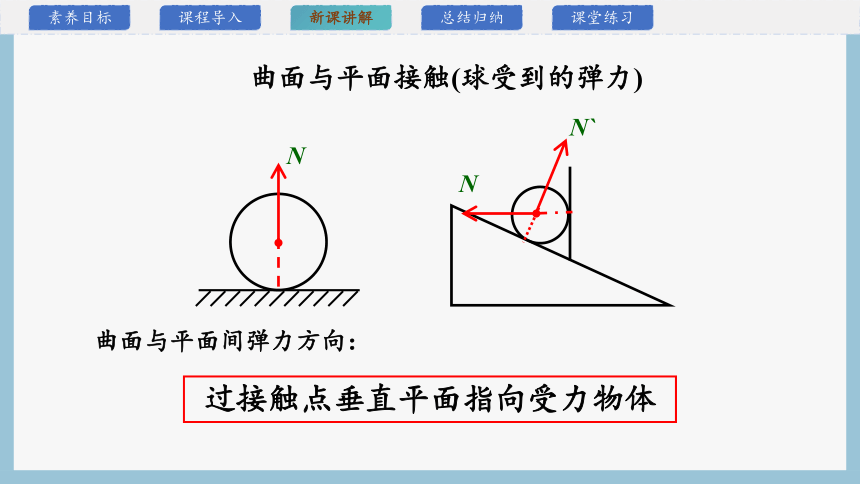
曲面与平面接触(球受到的弹力)
曲面与平面间弹力方向:
过接触点垂直平面指向受力物体
N
N
N`
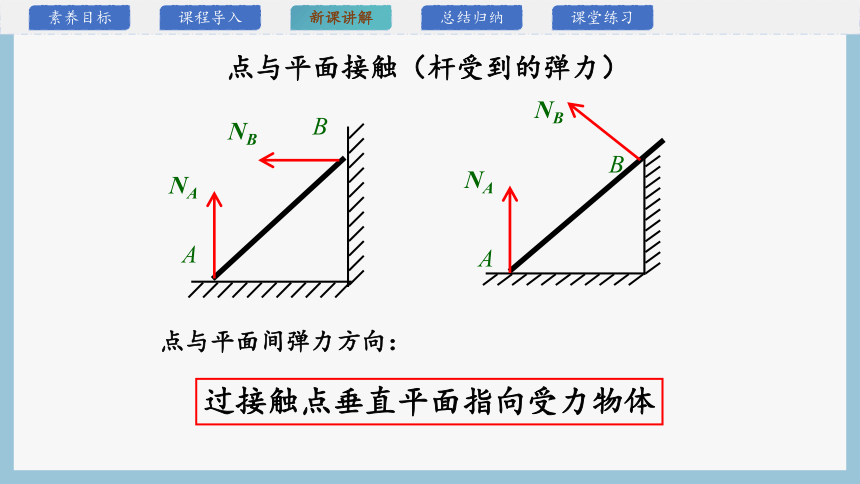
点与平面接触(杆受到的弹力)
点与平面间弹力方向:
过接触点垂直平面指向受力物体
A
B
NB
NA
A
B
NA
NB
点与曲面间弹力方向:
过接触点垂直切面指向受力物体
N1
N2
半球形的碗
A
B
NA
NB
点与曲面接触
曲面与曲面接触(球A受到的弹力)
半球形的碗
N
A
B
NB对A
N
曲面与曲面间弹力方向:
过接触点垂直公切面指向受力物体
(4)判断有无弹力的方法:
①直接法:对于形变效果明显的情况,可由形变情况直接判断弹力的存在与否。如弹簧、橡皮筋等产生弹力的情况。
②假设法:撤掉与之接触的物体,看放研究物体的状态是否改变,若改变则存在弹力,否则不存在弹力。
小心去掉斜面,球仍静止,说明斜面与球A之间无相互作用因而无弹力。
若去掉斜面,小球则无法保持在原来的位置静止,这说明斜面对小球有相互作用的弹力。
一个被吊着的均匀球壳,其内部注满了水,在球的底部有一带阀门的细出水口.在打开阀门让水慢慢流出的过程中,球壳与其中的水的共同重心将会 ( )
A.一直下降
B.一直不变
C.先下降后上升
D.先上升后下降
C
经典例题
关于弹力的产生说法正确的是( )
A.只要两物体接触就一定产生弹力
B.只要两物体相互吸引就一定产生弹力
C.只要物体发生形变就一定有弹力产生
D.只有发生弹性形变的物体才会对与它接触的物体产生弹力作用
D
经典例题
(多选)关于弹力的方向,下列说法正确的是( )
A.弹力方向一定垂直于接触面
B.弹力方向不一定垂直于接触面
C.轻质绳对物体的弹力方向一定沿着绳子离开物体的方向,因为绳子只会发生拉伸形变
D.轻质绳对物体产生的弹力一定垂直于与绳 相连的接触面
AC
经典例题
如图所示,已知小球静止,甲中的细线竖直,乙中的细线倾斜,试判断图中小球所受弹力的方向:
经典例题
一本书放在水平桌面上处于静止状态( )
A.书对桌面的压力就是书的重力
B.书对桌面的压力,是由于桌面发生了形变而产生的
C.书对桌面的压力在数值上等于它所受的重力
D.桌面对书的支持力和书对桌面的压力大小相等,所以书才处于平衡状态
经典例题
C
FN
G
FN
FN
正确教育
胡克定律
胡克定律最初是通过观察钟表中弹簧的伸缩发现的,该定律描述了材料受力时的变形情况。弹性材料的伸缩与其所受的力成正比。罗伯特·胡克是一位多产的科学家,对建筑学和科学均有贡献,不过奇怪的是他为人所知更多的是通过胡克定律。而胡克定律本身也正是跨越了诸多学科领域,在工程学、建筑学和材料科学中均有应用。
胡克定律的发现
质量大的胖子和质量小的瘦子站在同一弹簧上
弹力的大小:弹力的大小与形变的程度有关,对同一个物
体来讲,形变程度越大,弹力越大。
1、弹性形变:物体在发生形变后,如果撤去作用力能够恢复原状,这种形变叫作弹性形变。
2、弹性限度
如果形变过大,超过一定的限度,撤去作用力后物体不能完全恢复原来的形状,这个限度叫作弹性限度。
弹簧在形变时产生的弹力与弹簧的伸长量是有关系的。那么,弹簧在弹性限度内,弹力大小与其伸长量有什么关系呢?
1.实验思路:
(1)弹簧弹力F如何测量?
(2)弹簧的伸长量x如何测量?
弹簧下端悬挂的钩码静止时,弹簧弹力的大小与钩码的重力大小相等,即F=mg。
弹簧的原长l0与挂上钩码之后弹簧的总长度l可用刻度尺直接测出,弹簧的伸长量x=l-l0。
实验:探究弹簧弹力与形变量的关系
mg
F
l0
l
1.实验思路:
(3)如何能直观找出弹簧弹力与形变量的关系?
以纵坐标表示弹力大小F,以横坐标表示弹簧的形变量x,在坐标系中描出实验所测得的各组数据(F,x)对应的点,用平滑的曲线将这些点连接起来,根据实验所得的图线,即可探究弹簧弹力与形变量间的关系。
2.进行实验:
(1)按如图所示安装实验装置,记下弹簧下端不挂钩码时所对应的刻度l0。
(2)在弹簧下端悬挂一个钩码,平衡时记下弹簧的总长度和钩码所受的重力。
(3)增加钩码的个数,重复上述实验过程,将数据填入表格,以F表示弹力,l表示弹簧的总长度,x=l-l0表示弹簧的形变量。
2.进行实验:
(4)记录收集数据
1 2 3 4 5 6 7
F/N 0
l/cm
x/cm 0
3.数据处理:
(1)以弹力F(大小等于所挂钩码受到的重力)为纵坐标,以弹簧的形变量x为横坐标,用描点法作图。连接各点,得出弹力F随弹簧形变量x变化的图像。由实际作出的F x图像可知,图像为过原点的直线。
(2)以弹簧形变量为自变量,写出弹力和弹簧形变量之间的函数关系,函数表达式中常数即为弹簧的劲度系数,这个常数也可根据F x图像的斜率求解,k=ΔF/Δx。
3.数据处理:
(3)实验结论:实验结果表明,弹簧发生弹性形变时,弹力F的大小跟弹簧伸长(或缩短)的长度x成正比。
4、误差分析:
由于弹簧原长及伸长量的测量都不便于操作,存在较大的测量误差。
由于弹簧自身的重力的影响,当未放重物时,弹簧在自身重力的作用下,已经有一个伸长量,也会有一定的影响。
探究弹簧弹力与形变量的关系
思考:实验操作过程中有哪些注意事项?
所挂钩码不要过重,以免弹簧被过分拉伸,超出它的
弹性限度。
每次所挂钩码的质量差尽量大一些。
测弹簧长度时,一定要在弹簧竖直悬挂
且处于平衡状态时测量。
探究弹簧弹力与形变量的关系
1.内容:在弹性限度内,弹簧发生弹性形变时,弹力的大小F跟弹簧伸长(或缩短)的长度x成正比。
2.公式:F=kx
3.k为弹簧的劲度系数, 单位是N/m,只与弹簧本身有关,由弹簧本身的材料、长度、粗细、匝数等因素决定,它反映了弹簧的软硬程度,k越大,弹簧越硬,其长度越难改变.
胡克定律
在弹性限度内,弹簧弹力的变化量 F 与形变量的变化量 x 成正比
胡克定律的推论
① 弹力
(1)形变的分类:①弹性形变;②非弹性形变.
(2)弹力产生的条件:①接触;②物体发生形变.
(3)弹力的方向:垂直于接触面,并指向恢复形变的方向.
(4)弹力的大小:与形变物体的材料、形变量大小有关.
(5)弹簧弹力的大小:利用胡克定律 F = kx 计算,其中 k 是劲度系数,单位是牛顿每米,符号是 N/m.
2
可以完全恢复原状
不能完全恢复原状
弹力属于接触力,这一点与重力不同
作用线总是与两物体接触点的切面垂直
k 的大小反映弹簧的“硬”与“软”
一根大轻质弹簧内套着一根小轻质弹簧(二者不接触),大弹簧比小弹簧长0.2 m,它们的下端固定在地面上,上端自由,如图甲所示.当施加外力压缩此组合弹簧时,测得力和弹簧压缩距离之间的关系如图乙所示,则两根弹簧的劲度系数分别是(设大弹簧劲度系数为 k1,小弹簧劲度系数为 k2 )( )
A. k1 = 100 N/m,k2 = 200 N/m
B. k1 = 200 N/m,k2 = 100 N/m
C. k1 = 100 N/m,k2 = 300 N/m
D. k1 = 300 N/m,k2 = 200 N/m
A
答案:A
解析:大弹簧劲度系数为 ,小弹簧劲度系数为 ,
根据胡克定律 可知, 时,
有 时,
有 ,
联立解得 ,故A正确.
实验小组用如图甲所示的装置探究弹簧弹力与弹簧伸长量的关系,提供的器材有铁架台、弹簧、毫米刻度尺和多个钩码.测出弹簧原长后,将弹簧的一端固定在铁架台上,将毫米刻度尺竖直放在弹簧左侧.用悬挂钩码的方法给弹簧施加拉力,使弹簧保持竖直状态,当钩码稳定后读数,此时弹簧的弹力大小等于钩码的重力.
(1)某次测量弹簧的长度时,刻度尺的示数如图乙所示,读数为______cm.
(2)图丙是弹簧所受弹力 F 与弹簧伸长量 x 的 F-x 图像.根据此图像计算出弹簧劲度系数为______N/m.
(3)图丙中直线不过坐标原,点的原因是____________.
16.00
200
弹簧自身有重力
答案:(1)16.00 (2)200 (3)弹簧自身有重力
解析:(1)毫米刻度尺的分度值为0.1 cm,由题图丙可知读数为16.00 cm.
(2)根据胡克定律 可得, 图像的斜率表示弹簧的劲度系数,则
(3)由题图丙可知,当 时,x大于零,说明没有挂重物时,弹簧有伸长量,这是弹簧自身的重力造成的.
谢谢观看
1. 重力与弹力 第二课时
人教版(2019)物理(必修第一册)
第三章 相互作用——力
目录
素养目标
01
课程导入
02
新课讲解
03
总结归纳
04
课堂练习
05
正确教育
素养目标
1.知道重力产生的原因,理解重力的大小及方向,知道重心的概念
2.知道力的三要素,会用力的图示和示意图来表示力
3.知道弹力产生的原因和条件,会分析弹力的方向
4.能通过实验探究弹力的大小与形变量的关系
5.能根据数据表格绘制F-x图像,求出弹簧的劲度系数
6.知道胡克定律的内容及公式
经典回顾:2008北京奥运会——跳水女子3米板 郭晶晶夺得金牌
跳水板产生了明显的形变,这其中蕴含着怎样的物理知识呢?
正确教育
弹力
弹力
被拉长的弹簧,要恢复原状,对相连接的小车产生了拉力F;
F
被跳水运动员压弯的跳板,要恢复原状,对上面的人产生了支持力。
(1)定义:发生形变的物体,由于要恢复原状对跟它接触的物体产生力的作用,这种力叫弹力。
(2)产生条件:①直接接触;②发生弹性形变
F1
放在桌面上的书,它对桌面的压力F1以及桌面对它的支持力F2,都是弹力,其方向是跟接触面垂直指向被压或被支持的物体。
F2
弹力
由弹力的定义知,发生形变的物体(弹簧)由于要恢复原状,对与之接触的物体(小球)有弹力作用,所以弹力方向总是和施力物体发生形变的方向相反。
(3)弹力的方向
桌面形变
FN
物体形变
FN
物体受到支持力
桌面受到压力
1.有明显形变的情况下,根据物体的形变方向来判断:弹力的方向与物体形变的方向相反.如弹簧伸长时与伸长的方向相反,压缩时与压缩的方向相反.
2.发生微小形变时,形变方向不易观察,应根据物体间接触面特点进行分析:
①面面接触,弹力垂直于公共接触面
②点面接触,弹力过点垂直于接触面
③点点接触,弹力垂直于公切面
弹力方向的判断
面面接触
A
FA
β
FB
B
归纳:
弹簧被压缩时弹力沿伸长方向;被拉伸时弹力沿收缩方向
弹簧类
曲面与平面接触(球受到的弹力)
曲面与平面间弹力方向:
过接触点垂直平面指向受力物体
N
N
N`
点与平面接触(杆受到的弹力)
点与平面间弹力方向:
过接触点垂直平面指向受力物体
A
B
NB
NA
A
B
NA
NB
点与曲面间弹力方向:
过接触点垂直切面指向受力物体
N1
N2
半球形的碗
A
B
NA
NB
点与曲面接触
曲面与曲面接触(球A受到的弹力)
半球形的碗
N
A
B
NB对A
N
曲面与曲面间弹力方向:
过接触点垂直公切面指向受力物体
(4)判断有无弹力的方法:
①直接法:对于形变效果明显的情况,可由形变情况直接判断弹力的存在与否。如弹簧、橡皮筋等产生弹力的情况。
②假设法:撤掉与之接触的物体,看放研究物体的状态是否改变,若改变则存在弹力,否则不存在弹力。
小心去掉斜面,球仍静止,说明斜面与球A之间无相互作用因而无弹力。
若去掉斜面,小球则无法保持在原来的位置静止,这说明斜面对小球有相互作用的弹力。
一个被吊着的均匀球壳,其内部注满了水,在球的底部有一带阀门的细出水口.在打开阀门让水慢慢流出的过程中,球壳与其中的水的共同重心将会 ( )
A.一直下降
B.一直不变
C.先下降后上升
D.先上升后下降
C
经典例题
关于弹力的产生说法正确的是( )
A.只要两物体接触就一定产生弹力
B.只要两物体相互吸引就一定产生弹力
C.只要物体发生形变就一定有弹力产生
D.只有发生弹性形变的物体才会对与它接触的物体产生弹力作用
D
经典例题
(多选)关于弹力的方向,下列说法正确的是( )
A.弹力方向一定垂直于接触面
B.弹力方向不一定垂直于接触面
C.轻质绳对物体的弹力方向一定沿着绳子离开物体的方向,因为绳子只会发生拉伸形变
D.轻质绳对物体产生的弹力一定垂直于与绳 相连的接触面
AC
经典例题
如图所示,已知小球静止,甲中的细线竖直,乙中的细线倾斜,试判断图中小球所受弹力的方向:
经典例题
一本书放在水平桌面上处于静止状态( )
A.书对桌面的压力就是书的重力
B.书对桌面的压力,是由于桌面发生了形变而产生的
C.书对桌面的压力在数值上等于它所受的重力
D.桌面对书的支持力和书对桌面的压力大小相等,所以书才处于平衡状态
经典例题
C
FN
G
FN
FN
正确教育
胡克定律
胡克定律最初是通过观察钟表中弹簧的伸缩发现的,该定律描述了材料受力时的变形情况。弹性材料的伸缩与其所受的力成正比。罗伯特·胡克是一位多产的科学家,对建筑学和科学均有贡献,不过奇怪的是他为人所知更多的是通过胡克定律。而胡克定律本身也正是跨越了诸多学科领域,在工程学、建筑学和材料科学中均有应用。
胡克定律的发现
质量大的胖子和质量小的瘦子站在同一弹簧上
弹力的大小:弹力的大小与形变的程度有关,对同一个物
体来讲,形变程度越大,弹力越大。
1、弹性形变:物体在发生形变后,如果撤去作用力能够恢复原状,这种形变叫作弹性形变。
2、弹性限度
如果形变过大,超过一定的限度,撤去作用力后物体不能完全恢复原来的形状,这个限度叫作弹性限度。
弹簧在形变时产生的弹力与弹簧的伸长量是有关系的。那么,弹簧在弹性限度内,弹力大小与其伸长量有什么关系呢?
1.实验思路:
(1)弹簧弹力F如何测量?
(2)弹簧的伸长量x如何测量?
弹簧下端悬挂的钩码静止时,弹簧弹力的大小与钩码的重力大小相等,即F=mg。
弹簧的原长l0与挂上钩码之后弹簧的总长度l可用刻度尺直接测出,弹簧的伸长量x=l-l0。
实验:探究弹簧弹力与形变量的关系
mg
F
l0
l
1.实验思路:
(3)如何能直观找出弹簧弹力与形变量的关系?
以纵坐标表示弹力大小F,以横坐标表示弹簧的形变量x,在坐标系中描出实验所测得的各组数据(F,x)对应的点,用平滑的曲线将这些点连接起来,根据实验所得的图线,即可探究弹簧弹力与形变量间的关系。
2.进行实验:
(1)按如图所示安装实验装置,记下弹簧下端不挂钩码时所对应的刻度l0。
(2)在弹簧下端悬挂一个钩码,平衡时记下弹簧的总长度和钩码所受的重力。
(3)增加钩码的个数,重复上述实验过程,将数据填入表格,以F表示弹力,l表示弹簧的总长度,x=l-l0表示弹簧的形变量。
2.进行实验:
(4)记录收集数据
1 2 3 4 5 6 7
F/N 0
l/cm
x/cm 0
3.数据处理:
(1)以弹力F(大小等于所挂钩码受到的重力)为纵坐标,以弹簧的形变量x为横坐标,用描点法作图。连接各点,得出弹力F随弹簧形变量x变化的图像。由实际作出的F x图像可知,图像为过原点的直线。
(2)以弹簧形变量为自变量,写出弹力和弹簧形变量之间的函数关系,函数表达式中常数即为弹簧的劲度系数,这个常数也可根据F x图像的斜率求解,k=ΔF/Δx。
3.数据处理:
(3)实验结论:实验结果表明,弹簧发生弹性形变时,弹力F的大小跟弹簧伸长(或缩短)的长度x成正比。
4、误差分析:
由于弹簧原长及伸长量的测量都不便于操作,存在较大的测量误差。
由于弹簧自身的重力的影响,当未放重物时,弹簧在自身重力的作用下,已经有一个伸长量,也会有一定的影响。
探究弹簧弹力与形变量的关系
思考:实验操作过程中有哪些注意事项?
所挂钩码不要过重,以免弹簧被过分拉伸,超出它的
弹性限度。
每次所挂钩码的质量差尽量大一些。
测弹簧长度时,一定要在弹簧竖直悬挂
且处于平衡状态时测量。
探究弹簧弹力与形变量的关系
1.内容:在弹性限度内,弹簧发生弹性形变时,弹力的大小F跟弹簧伸长(或缩短)的长度x成正比。
2.公式:F=kx
3.k为弹簧的劲度系数, 单位是N/m,只与弹簧本身有关,由弹簧本身的材料、长度、粗细、匝数等因素决定,它反映了弹簧的软硬程度,k越大,弹簧越硬,其长度越难改变.
胡克定律
在弹性限度内,弹簧弹力的变化量 F 与形变量的变化量 x 成正比
胡克定律的推论
① 弹力
(1)形变的分类:①弹性形变;②非弹性形变.
(2)弹力产生的条件:①接触;②物体发生形变.
(3)弹力的方向:垂直于接触面,并指向恢复形变的方向.
(4)弹力的大小:与形变物体的材料、形变量大小有关.
(5)弹簧弹力的大小:利用胡克定律 F = kx 计算,其中 k 是劲度系数,单位是牛顿每米,符号是 N/m.
2
可以完全恢复原状
不能完全恢复原状
弹力属于接触力,这一点与重力不同
作用线总是与两物体接触点的切面垂直
k 的大小反映弹簧的“硬”与“软”
一根大轻质弹簧内套着一根小轻质弹簧(二者不接触),大弹簧比小弹簧长0.2 m,它们的下端固定在地面上,上端自由,如图甲所示.当施加外力压缩此组合弹簧时,测得力和弹簧压缩距离之间的关系如图乙所示,则两根弹簧的劲度系数分别是(设大弹簧劲度系数为 k1,小弹簧劲度系数为 k2 )( )
A. k1 = 100 N/m,k2 = 200 N/m
B. k1 = 200 N/m,k2 = 100 N/m
C. k1 = 100 N/m,k2 = 300 N/m
D. k1 = 300 N/m,k2 = 200 N/m
A
答案:A
解析:大弹簧劲度系数为 ,小弹簧劲度系数为 ,
根据胡克定律 可知, 时,
有 时,
有 ,
联立解得 ,故A正确.
实验小组用如图甲所示的装置探究弹簧弹力与弹簧伸长量的关系,提供的器材有铁架台、弹簧、毫米刻度尺和多个钩码.测出弹簧原长后,将弹簧的一端固定在铁架台上,将毫米刻度尺竖直放在弹簧左侧.用悬挂钩码的方法给弹簧施加拉力,使弹簧保持竖直状态,当钩码稳定后读数,此时弹簧的弹力大小等于钩码的重力.
(1)某次测量弹簧的长度时,刻度尺的示数如图乙所示,读数为______cm.
(2)图丙是弹簧所受弹力 F 与弹簧伸长量 x 的 F-x 图像.根据此图像计算出弹簧劲度系数为______N/m.
(3)图丙中直线不过坐标原,点的原因是____________.
16.00
200
弹簧自身有重力
答案:(1)16.00 (2)200 (3)弹簧自身有重力
解析:(1)毫米刻度尺的分度值为0.1 cm,由题图丙可知读数为16.00 cm.
(2)根据胡克定律 可得, 图像的斜率表示弹簧的劲度系数,则
(3)由题图丙可知,当 时,x大于零,说明没有挂重物时,弹簧有伸长量,这是弹簧自身的重力造成的.
谢谢观看
