北师大版八年级上册第二章《2.6 实数》导学案(无答案)
文档属性
| 名称 | 北师大版八年级上册第二章《2.6 实数》导学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 79.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-24 17:07:37 | ||
图片预览



文档简介
2.6
实数(1)
一、学习目标
1.了解无理数和实数的概念,能按要求对实数进行分类。
2.了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。进一步领会数形结合的思想。
3.会求实数的相反数和绝对值。
二、问题导学(教材P82-84)
●温故知新
把下列有理数写成小数的形式,你能发现什么?
3,
,
,
,
,
。
①任何一个有理数都可以写成
小数或
小数的形式。②反过来,任何
小数或
小数都是有理数。
2.回顾有理数分类,画出有理数的分类图。
什么叫数轴?把下列各数在数轴上表示出来
1.5
-3
●投石问路
1.什么叫无理数?
在前面我们学习了求一个数的平方根和立方根时,有些数的平方根或立方根是无限不循环小数,。。如:…都是无理数,π=3.14159265…也是无理数。我们把无限不循环小数叫做无理数。
小结:我们目前学习的无理数有下面三种形式
开方开不尽的数,如:,,,…②圆周率π,它是无限不循环小数
③类似0.1010010001…(每两个1之间依次多1个1)
2.
用根号表示的数一定是无理数吗?举例说明
3.
尝试画出无理数分类图。
●问题摘要:
三、问题探究
●问题指导
(一)什么叫实数?如何分类?
1.实数的定义:
和
统称实数。
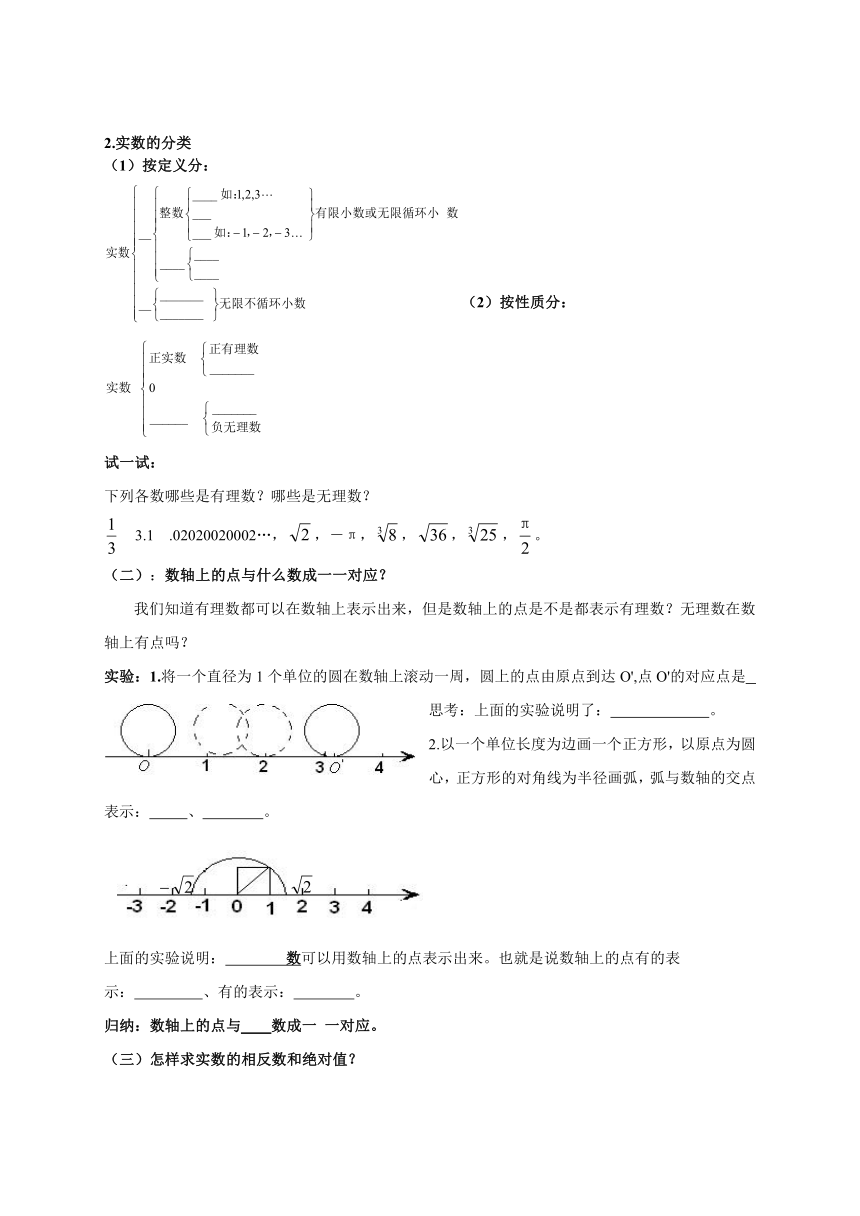
2.实数的分类
(1)按定义分:
(2)按性质分:
试一试:
下列各数哪些是有理数?哪些是无理数?
3.1
.02020020002…,,-π,,,,。
(二):数轴上的点与什么数成一一对应?
我们知道有理数都可以在数轴上表示出来,但是数轴上的点是不是都表示有理数?无理数在数轴上有点吗?
实验:1.将一个直径为1个单位的圆在数轴上滚动一周,圆上的点由原点到达O',点O'的对应点是
思考:上面的实验说明了:
。
2.以一个单位长度为边画一个正方形,以原点为圆心,正方形的对角线为半径画弧,弧与数轴的交点表示:
、
。
上面的实验说明:
数可以用数轴上的点表示出来。也就是说数轴上的点有的表示:
、有的表示:
。
归纳:数轴上的点与
数成一
一对应。
(三)怎样求实数的相反数和绝对值?
在数轴上一个实数的绝对值是表示这个数的点
( http: / / www.21cnjy.com )到
的距离:两个互为相反数的实数就是表示这两个数的点一个在
,一个在
,它们到原点的距离
。
试试看:(1)相反数:π的相反数是
,
的相反数是
,0的相反数是
。..
小结:实数的相反数是
。
(2)绝对值:=
,=
,
=
,=
,
小结:一个正实数的绝对值
,一个负实数的绝对值是
,0的绝对值是
。
●问题检测
1.下列各数,一定是无理数的是(
)
A.带根号的数
B.无限小数
C.不循环小数
D.无限不循环小数
2.在实数5、、、中,无理数是(
)
A.5
B.
C.
D.
3.
的相反数是
,绝对值是的数是
。
●问题梳理
●问题拓展
的相反数
,的相反数
;
四、问题达标(用时
分钟,得分:
)
1.和数轴上的点一一对应的是(
)
A.整数
B.有理数
C.无理数
D.实数
2.在实数π,,,,0.2121121112…(每两个2之间依次多1个1),中,无理数共有(
)
A.2个
B.3个
C.4个
D.5个
3.有一个数值转换器,原理如图,当输入的为64时,输出的是(
)
A.8
B.
C.4
D.2
4.已知实数和互为相反数,实数和互为倒数,的倒数等于它本身,则-
=
。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
2.6
实数(2)
一、学习目标
1.学会比较两个实数的大小,能熟练地进行实数运算。
2.
进一步领会数形结合的思想。
二、问题导学(教材P85-86)
●温故知新
1.在数轴上表示的数,右边的数总比左边的数
。
2.计算:=
,=
,=
,
=
,=
,=
。
3.计算:=
。
4.计算的结果是(
)
A.3
B.7
C.-3
D.
-7
●投石问路
1.有理数中的运算法则及性质是否在实数范围内也适用呢?
2.实数如何进行的大小比较呢?
比较大小:
2,
=
,
π
3.=
,=
。
●问题摘要:
三、问题探究
●问题指导
(一)实数的大小比较
下列式中,正确的是(
)
A.
B.
C.
D.
小结:进行实数的大小比较时,应把各数统一转化成一种形式。如:第1题,把10转化成,把11转化成,把12转化成,
把1,32转化成,再比较大小,较简便。
(二)实数的运算
1.计算:
(1)
(2)
2.小结:实数运算中,有理数的运算法则及运算性质等同样适用。
3.
计算下列各式的值:
(1)
(2)
(三)实数运算求近似值
计算(结果保留小数点后两位)
(1)
(2)
●问题检测
1.
P87第6题
2.(
)
A.互为相反数
B.互为倒数
C.相等
D.以上都不对
3.化简:
(1)=
;
(2)=
。
4.若。
5.
,5.-3,,的大小顺序是(
)
A.
<-3<<
B.
<-3<<
C.
-3<<<
D.
-3<<<
6.计算与化简:
7.
P86练习第3题
●问题梳理
●问题拓展
1.化简:
2.
四、问题达标(用时
分钟,得分:
)
1.
等于(
)
A.
B.3
C.
D.1
2.
等于(
)
A.
B.2
C.1
D.0
3.下列四个数中与最接近的数是(
)
A.2
B.3
C.4
D.5
4.在下列各式中,正确的是(
)
A.
B.
C.
D.
5.计算下列各式
(1)
(2)
6.如图所示,在平行四边形ABCO中,已知A、C两点的坐标为A(,),C(2,0).
(1)求点B的得坐标;
(2)求平行四边形ABCO向左平移个单位长度后所得四边形的A′B′C′D′四个顶点的坐标;
(3)求平行四边形ABCO的面积。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
试试看
实数(1)
一、学习目标
1.了解无理数和实数的概念,能按要求对实数进行分类。
2.了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。进一步领会数形结合的思想。
3.会求实数的相反数和绝对值。
二、问题导学(教材P82-84)
●温故知新
把下列有理数写成小数的形式,你能发现什么?
3,
,
,
,
,
。
①任何一个有理数都可以写成
小数或
小数的形式。②反过来,任何
小数或
小数都是有理数。
2.回顾有理数分类,画出有理数的分类图。
什么叫数轴?把下列各数在数轴上表示出来
1.5
-3
●投石问路
1.什么叫无理数?
在前面我们学习了求一个数的平方根和立方根时,有些数的平方根或立方根是无限不循环小数,。。如:…都是无理数,π=3.14159265…也是无理数。我们把无限不循环小数叫做无理数。
小结:我们目前学习的无理数有下面三种形式
开方开不尽的数,如:,,,…②圆周率π,它是无限不循环小数
③类似0.1010010001…(每两个1之间依次多1个1)
2.
用根号表示的数一定是无理数吗?举例说明
3.
尝试画出无理数分类图。
●问题摘要:
三、问题探究
●问题指导
(一)什么叫实数?如何分类?
1.实数的定义:
和
统称实数。
2.实数的分类
(1)按定义分:
(2)按性质分:
试一试:
下列各数哪些是有理数?哪些是无理数?
3.1
.02020020002…,,-π,,,,。
(二):数轴上的点与什么数成一一对应?
我们知道有理数都可以在数轴上表示出来,但是数轴上的点是不是都表示有理数?无理数在数轴上有点吗?
实验:1.将一个直径为1个单位的圆在数轴上滚动一周,圆上的点由原点到达O',点O'的对应点是
思考:上面的实验说明了:
。
2.以一个单位长度为边画一个正方形,以原点为圆心,正方形的对角线为半径画弧,弧与数轴的交点表示:
、
。
上面的实验说明:
数可以用数轴上的点表示出来。也就是说数轴上的点有的表示:
、有的表示:
。
归纳:数轴上的点与
数成一
一对应。
(三)怎样求实数的相反数和绝对值?
在数轴上一个实数的绝对值是表示这个数的点
( http: / / www.21cnjy.com )到
的距离:两个互为相反数的实数就是表示这两个数的点一个在
,一个在
,它们到原点的距离
。
试试看:(1)相反数:π的相反数是
,
的相反数是
,0的相反数是
。..
小结:实数的相反数是
。
(2)绝对值:=
,=
,
=
,=
,
小结:一个正实数的绝对值
,一个负实数的绝对值是
,0的绝对值是
。
●问题检测
1.下列各数,一定是无理数的是(
)
A.带根号的数
B.无限小数
C.不循环小数
D.无限不循环小数
2.在实数5、、、中,无理数是(
)
A.5
B.
C.
D.
3.
的相反数是
,绝对值是的数是
。
●问题梳理
●问题拓展
的相反数
,的相反数
;
四、问题达标(用时
分钟,得分:
)
1.和数轴上的点一一对应的是(
)
A.整数
B.有理数
C.无理数
D.实数
2.在实数π,,,,0.2121121112…(每两个2之间依次多1个1),中,无理数共有(
)
A.2个
B.3个
C.4个
D.5个
3.有一个数值转换器,原理如图,当输入的为64时,输出的是(
)
A.8
B.
C.4
D.2
4.已知实数和互为相反数,实数和互为倒数,的倒数等于它本身,则-
=
。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
2.6
实数(2)
一、学习目标
1.学会比较两个实数的大小,能熟练地进行实数运算。
2.
进一步领会数形结合的思想。
二、问题导学(教材P85-86)
●温故知新
1.在数轴上表示的数,右边的数总比左边的数
。
2.计算:=
,=
,=
,
=
,=
,=
。
3.计算:=
。
4.计算的结果是(
)
A.3
B.7
C.-3
D.
-7
●投石问路
1.有理数中的运算法则及性质是否在实数范围内也适用呢?
2.实数如何进行的大小比较呢?
比较大小:
2,
=
,
π
3.=
,=
。
●问题摘要:
三、问题探究
●问题指导
(一)实数的大小比较
下列式中,正确的是(
)
A.
B.
C.
D.
小结:进行实数的大小比较时,应把各数统一转化成一种形式。如:第1题,把10转化成,把11转化成,把12转化成,
把1,32转化成,再比较大小,较简便。
(二)实数的运算
1.计算:
(1)
(2)
2.小结:实数运算中,有理数的运算法则及运算性质等同样适用。
3.
计算下列各式的值:
(1)
(2)
(三)实数运算求近似值
计算(结果保留小数点后两位)
(1)
(2)
●问题检测
1.
P87第6题
2.(
)
A.互为相反数
B.互为倒数
C.相等
D.以上都不对
3.化简:
(1)=
;
(2)=
。
4.若。
5.
,5.-3,,的大小顺序是(
)
A.
<-3<<
B.
<-3<<
C.
-3<<<
D.
-3<<<
6.计算与化简:
7.
P86练习第3题
●问题梳理
●问题拓展
1.化简:
2.
四、问题达标(用时
分钟,得分:
)
1.
等于(
)
A.
B.3
C.
D.1
2.
等于(
)
A.
B.2
C.1
D.0
3.下列四个数中与最接近的数是(
)
A.2
B.3
C.4
D.5
4.在下列各式中,正确的是(
)
A.
B.
C.
D.
5.计算下列各式
(1)
(2)
6.如图所示,在平行四边形ABCO中,已知A、C两点的坐标为A(,),C(2,0).
(1)求点B的得坐标;
(2)求平行四边形ABCO向左平移个单位长度后所得四边形的A′B′C′D′四个顶点的坐标;
(3)求平行四边形ABCO的面积。
五、学习反思
1.本节有哪些收获?(知识上,思想方法上)
2.课前的疑难解决了吗?有没有新的问题?
试试看
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
