青岛版六年级数学下册期末专项训练:解答题(含解析)
文档属性
| 名称 | 青岛版六年级数学下册期末专项训练:解答题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 358.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 13:56:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
青岛版六年级数学下册期末专项训练:解答题
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.一个煤堆近似圆锥体,煤堆底面周长是37.68m,高3m,1m3煤重1.4吨,这堆煤大约重多少吨?(得数保留一位小数)
2.用地砖铺设一块地板,用2平方米的地砖,需要25块,那么用5平方米的地砖,需要多少块?
3.王奶奶有5000元钱,准备存入银行5年,年利率为4.02%,五年后王奶奶能得到本息多少元?
4.橙汁罐为圆柱形,底面直径为6厘米,高为11厘米。将24罐橙汁放入箱内,这个箱子的长、宽、高分别是多少厘米
5.新景小学有1300名学生,其中50%是住校生,你知道住校生有多少名吗?
6.下面是张大爷的一-张储蓄存单,他的存款到期时实际可得多少元利息?
中国建设银行(定期)储蓄存单 账号×××××× 币种人民币 金额(大写)五万元 小写¥50000元
存入期 存期 年利率 起息日 到期日
2010年4月1日 5年 4.75% 2010年4月1日 2015年4月1日
7.一个底面直径是4dm的圆柱形木桶,高6dm。这个木桶破损后(如图)最多能盛多少L水?
8.下面是某小学六年级学生的视力情况统计图.近视人数占全年级学生人数的百分之几 视力不良(包括假性近视和近视)的人数占全年级学生人数的百分之几
9.一个竹筒从里面量直径为6厘米,长为10厘米。把大米装至竹筒长的处做米饭,如果每立方厘米大米重3克,这根竹筒里的大米重多少克?
10.2022年第24届冬季奥运会在北京和张家口举办,北京至张家口的距离约是180千米,在一幅冬奥会宣传图上,两地间的图上距离是60厘米。
(1)这幅宣传图的比例尺是多少?
(2)在这幅宣传图上京张高铁全线长58厘米,京张高铁实际全线长多少千米?
11.判断成不成比例.如果成比例,成什么比例
(1)比的后项一定,它的前项和比值.
(2)打一份稿件,每分钟打字的个数和所需要的时间.
(3)强强跳高的高度与他的身高.
12.一家房地产开发商12月份的营业额是5000万元.如果按营业额的5%缴纳营业税,这家房地产开发商应该缴纳营业税多少万元
13.甲数除乙数的商是1.8,那么甲数与乙数的比是多少?
14.甲、乙两城实际距离是1200千米,画在比例尺是1∶30000000的地图上,两地之间的图上距离是多少厘米?
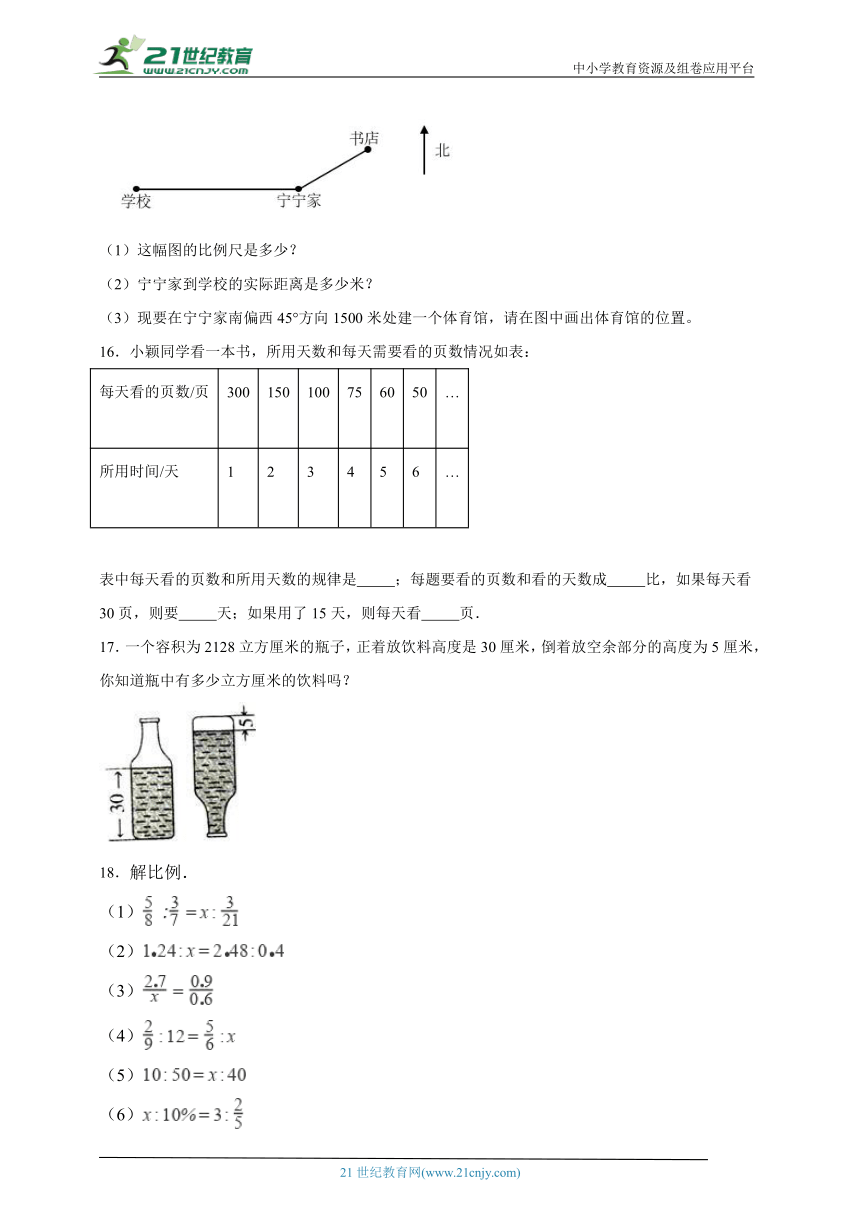
15.如图,宁宁家距书店1000米。
(1)这幅图的比例尺是多少?
(2)宁宁家到学校的实际距离是多少米?
(3)现要在宁宁家南偏西45°方向1500米处建一个体育馆,请在图中画出体育馆的位置。
16.小颖同学看一本书,所用天数和每天需要看的页数情况如表:
每天看的页数/页 300 150 100 75 60 50 …
所用时间/天 1 2 3 4 5 6 …
表中每天看的页数和所用天数的规律是 ;每题要看的页数和看的天数成 比,如果每天看30页,则要 天;如果用了15天,则每天看 页.
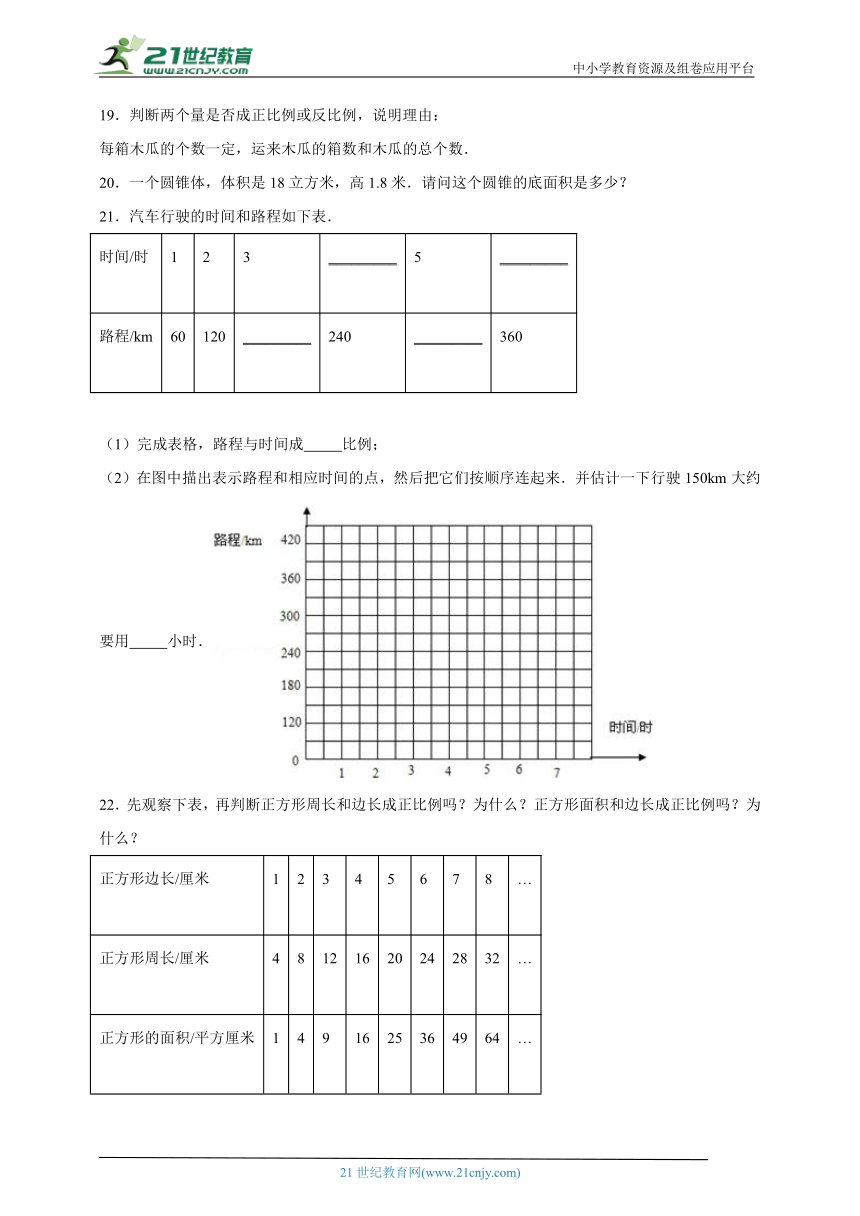
17.一个容积为2128立方厘米的瓶子,正着放饮料高度是30厘米,倒着放空余部分的高度为5厘米,你知道瓶中有多少立方厘米的饮料吗?
18.解比例.
(1)
(2)
(3)
(4)
(5)
(6)
19.判断两个量是否成正比例或反比例,说明理由:
每箱木瓜的个数一定,运来木瓜的箱数和木瓜的总个数.
20.一个圆锥体,体积是18立方米,高1.8米.请问这个圆锥的底面积是多少?
21.汽车行驶的时间和路程如下表.
时间/时 1 2 3 _________ 5 _________
路程/km 60 120 _________ 240 _________ 360
(1)完成表格,路程与时间成 比例;
(2)在图中描出表示路程和相应时间的点,然后把它们按顺序连起来.并估计一下行驶150km大约要用 小时.
22.先观察下表,再判断正方形周长和边长成正比例吗?为什么?正方形面积和边长成正比例吗?为什么?
正方形边长/厘米 1 2 3 4 5 6 7 8 …
正方形周长/厘米 4 8 12 16 20 24 28 32 …
正方形的面积/平方厘米 1 4 9 16 25 36 49 64 …
23.用一个底面为边长8厘米的正方形,高为16厘米的长方体容器,测量一个铅锤的体积,容器中装的水距容器口还有2厘米。当铅垂放入容器中,有部分水溢出;当把铅锤取出后,水面比原来下降了5厘米。这个铅锤的体积是多少立方厘米?
24.小萌读一本100页的故事书,第一天读了这本书的20%,第二天读了这本书的35%,第一天比第二天少读多少页
25.把一根4m长的圆木锯成4段短圆木,表面积比原来增加了48dm2,这根圆木原来的体积是多少?
26.以图的直角三角形的一条边为轴,旋转一周,求得到的形体的体积.
27.张倩用电脑练习打字,前4分钟打了60个字,照这样计算,一篇900字的文章一共需要打多长时间?
(1)已知条件里相关联的两种量是 和 .
(2)根据“照这样计算”这句话,说明张倩每分钟打字的 是一定的.
(3)说明这两种相关联的量成 比例.也就是说这两种量中相对应的两个数的 一定.
(4)因此用比例知识解答列式为(用x表示所求问题): ○ = ○ .
28.一个圆锥体的体积是80立方厘米,底面积是16平方厘米,它的高是多少厘米?
29.手工制作课上,六年级二班制作红花30朵,黄花24朵,黄花比红花少百分之几?
30.求下列图形的体积(单位:cm)
31.如图是一个长方形.请你想象一下,以一条长边为轴旋转一周,可以形成一个 .并计算出它的体积.(单位:厘米)
32.圆柱的底面直径是7厘米,高是8厘米,求侧面积.
33.如果把两种相关联的量用a、b表示,你能判断下列哪个式子表示成正比例吗?
a+b=12 a-b=3.8 ab= a:b=5
34.王庄小学六年级一班的学生人数是六年级二班学生人数的90%,六年级一班的人数比六年级二班少4人.六年级一班有多少人
35.一个圆柱的底面积是12.56平方厘米,侧面积是62.8平方厘米,它的表面积是 平方厘米.
36.任意圆的周长与任意半径成正比例. .
37.有一只圆柱形玻璃杯,测得内直径是8厘米,内装药水的深度是5厘米,正好是杯内容量的,再加多少毫升药水可以把杯子盛满?
38.一个容器内已注满水,有大、中、小三个球。第一次把小球沉入水中;第二次把小球取出,把中球沉入水中;第三次取出中球,把小球和大球一起沉入水中,现在知道每次从容器中溢出水量的情况是,第一次是第二次的,第三次是第一次的2.5倍,求三个球的体积之比。
39.小明沿6米长的路走了3次,第一次10步走完,第二次9步走完,第三次11步走完.
(1)他平均一步的长度是多少米
(2)他沿着一个圆形花坛走了一圈,刚好是157步,这个花坛的面积约是多少平方米
40.一个圆柱形的油桶,桶内底面直径是30厘米,高40厘米,桶里盛满汽油.如果把桶里汽油全部倒进一个长方体油箱,油箱还空着.这个油箱的底面积是471平方厘米.这个油箱的高有多少厘米?
《青岛版六年级数学下册期末专项训练:解答题》参考答案
1.158.3吨
【分析】要求这堆煤的重量,先求得煤的体积,煤堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,进一步再求煤的重量,问题得解。
【详解】煤堆的体积:
×3.14×(37.68÷3.14÷2)2×3
=3.14×62
=3.14×36
=113.04(立方米);
煤堆的重量:
113.04×1.4≈158.3(吨);
答:这堆煤约重158.3吨。
【点睛】此题主要考查圆锥的体积计算公式V=r2h,运用公式计算时不要漏乘。
2.10块
【详解】2×25÷5=10(块)
答:用5平方米的地砖,需要10块。
3.6005元
【详解】5000×4.02%×5+5000=6005(元)
答:五年后王奶奶能得到本息6005元。
4.长:36厘米;宽:24厘米;高:11厘米
【分析】根据图片可知,箱子的长是6个橙汁罐底面直径的距离,所用要求这个箱子的长度就是求6个6厘米是多少,用乘法计算;箱子的宽是4个橙汁罐底面直径的距离,所用要求这个箱子的宽度就是求4个6厘米是多少,用乘法计算;箱子的高就是橙汁罐的高度,据此解答。
【详解】长:
宽:
高:11厘米
答:这个箱子的长是36厘米,宽是24厘米,高是11厘米。
【点睛】认真观察给出的图片:充分理解这个箱子的长、宽、高与橙汁罐之间的数量关系。
5.650名
【分析】根据题意,新景小学有1300名学生,其中有50%是住校生,用1300×50%,就是住校生的人数。
【详解】1300×50%=650(名)
答:住校生有650名。
【点睛】本题考查求一个数的百分之几是多少,用乘法。
6.11875元
【分析】根据利息公式:利息=本金×利率×时间,代入数据,即可求出到期的利息。
【详解】50000×4.75%×5
=2375×5
=11875(元)
答:他的存款到期时实际可得11875元。
7.69.08L
【分析】观察图形可知,水桶能盛水的最高高度是6dm-5cm=5.5dm,由此再利用圆柱的容积公式即可解答。
【详解】5cm=0.5dm
3.14×(4÷2)2×(6-0.5)
=3.14×4×5.5
=69.08(dm3)
=69.08(L)
答:这个木桶破损后最多能盛69.08L水。
【点睛】此题主要考查圆柱的容积公式的灵活应用,注意确定水桶的储水高度。
8.29%,59%
【详解】解:1-(30%+41%)=29%
1-41%=59%
答:近视人数占全年级学生人数的29%,视力不良(包括假性近视和近视)的人数占全年级学生人数的59%.
9.847.8克
【分析】先求出竹筒的体积,用竹筒体积的就是大米的体积,用大米的体积乘3,就是大米的重量。
【详解】
=
=
=(克)
答:这根竹筒里的大米重847.8克。
【点睛】重点是求出大米的体积,根据的大米的体积求重量。
10.(1)1∶300000;
(2)174千米。
【分析】(1)根据比例尺的定义,比例尺是图上距离与实际距离的比,把图上距离与实际距离的单元统一一下代入公式即可得解;
(2)根据(1)中得出的比例尺,利用比例的性质即可得解。
【详解】(1)180千米=18000000厘米
60∶18000000=1∶300000
答:这幅宣传图的比例尺是1∶300000。
(2)图上1厘米表示300000厘米,即1厘米表示3千米,
3×58=174(千米)
答:京张高铁实际全线长174千米。
11.(1)成正比例 (2)成反比例 (3)不成比例
【详解】略
12.5000×5%=250(万元)
【详解】略
13.甲:乙=5:9
【分析】甲数除乙数,即乙÷甲=1.8=9/5,由此求出甲乙的比
【详解】甲:乙=1:1.8=5:9
14.4厘米
【分析】这道题是已知比例尺、实际距离,求图上距离,根据图上距离=实际距离×比例尺,解答即可。
【详解】1200千米=120000000厘米
120000000×=4(厘米)
答:两地之间的图上距离是4厘米。
【点睛】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题。
15.(1)1∶50000;
(2)2000米;
(3)见详解
【分析】(1)通过直尺测量,宁宁家到书店的图上距离是2厘米,宁宁家距书店1000米,统一单位后,根据比例尺的意义,比例尺=图上距离∶实际距离,代入数据求出这幅图的比例尺。
(2)经测量,宁宁家到学校的图上距离是4厘米,根据实际距离=图上距离÷比例尺,代入数据即可求出宁宁家到学校的实际距离是多少米。
(3)统一单位后,用实际距离×比例尺=图上距离,求出体育馆和宁宁家两地之间的图上距离,再以宁宁家为观测点,利用地图上的方向“上北下南,左西右东”,根据方向、角度、距离确定体育馆的位置,并在图上标注出来。
【详解】(1)1000米=100000厘米
2∶100000=1∶50000
答:这幅图的比例尺是1∶50000。
(2)4÷
=4×50000
=200000(厘米)
200000厘米=2000米
答:宁宁家到学校的实际距离是2000米。
(3)1500米=150000厘米
150000×=3(厘米)
如图:
【点睛】此题主要考查比例尺的意义以及根据方向、角度、距离确定物体的位置。
16.乘积相等,反,10.20.
【详解】试题分析:表中每天看的页数和所用天数的乘积相等,符合反比例的意义;进而根据每天看的页数和所用天数的乘积相等,列出方程或比例,解答后面的两个问题即可.
解:(1)每天看的页数和所用天数的乘积相等,
所以符合反比例的意义,则每天要看的页数和看的天数成反比例关系;
(2)设如果每天看30页,则要x天看完,由题意得:
30x=50×6,
30x÷30=300÷30,
x=10;
答:如果每天看30页,则要10天看完.
(3)设如果用了15天,则每天看x页,由题意得:
15x=50×6,
15x÷15=300÷15,
x=20;
答:如果用了15天,则每天看20页.
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
17.2128÷(30+5)×30
=2128÷35×30
=60.8×30
=1824(立方厘米)
答:瓶中有1824立方厘米的饮料.
【详解】瓶子的容积可以分为两部分,一部分是饮料部分是一个高30厘米的圆柱体,另一部分是空余部分是一个高5厘米的圆柱体,由此可以求出瓶子的底面积;再根据底面积乘高就可以求出饮料的体积.
18.(1)
(2)
(3)
(4)
(5)
(6)
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积.
【详解】(1)
解:
(2)
解:
(3)
解:
(4)
解:
(5)10:50=x:40
解: 50x=10×40
50x=400
x=8
(6)
解:
19.成反比例.
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:因为:木瓜的总个数÷木瓜的箱数=每箱木瓜的个数(一定),所以运来木瓜的箱数和木瓜的总个数成正比例.
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
20.30平方米
【详解】试题分析:根据圆锥的体积公式:v=sh,s=vh,把数据代入公式解答.
解:181.8,
=18×3÷1.8,
=54÷1.8,
=30(平方米);
答:这个圆柱的底面积是30平方米.
点评:此题主要考查圆锥的体积公式的灵活运用.
21.(1)180,4,300,6.正比例.(2)2.5小时.
【详解】试题分析:(1)因为=60,=60,60是一定的数,代表速度,速度(一定),所以路程和时间成正比例,设要填的数为x,列出比例,求出x的值即可,同样求出其它要填的数;
(2)时间:1小时,路程60千米;时间:2小时,路程120千米;时间:3小时,路程180千米;时间:4小时,路程240千米;时间:5小时,路程300千米;时间:6小时,路程360千米,描出表示路程和相应时间的点,然后把它们按顺序连起来.
速度(一定),所以路程和时间成正比例,设行150千米用x小时,列并解比例即可.
解:(1)因为=60,
=60,
因为60是一定的数,代表速度,
速度(一定),所以路程和时间成正比例.
设要填的数为x,
=,
x=180;
答:3小时行180千米;
设要填的数为y,
=,
60y=240,
60y÷60=240÷60,
y=4;
答:行240千米需要4小时;
设要填的数为a,
=,
a=300;
答:5小时行300千米;
设要填的数为b,
=,
60b=360,
60b÷60=360÷60,
b=6.
答:行360千米需要6小时.
(2)时间:1小时,路程60千米;时间:2小时,路程120千米;时间:3小时,路程180千米;时间:4小时,路程240千米;时间:5小时,路程300千米;时间:6小时,路程360千米,描出表示路程和相应时间的点,然后把它们按顺序连起来.
因为速度一定,路程和时间成正比例,
设大约要用x小时,
=,
60x=150,
60x÷60=150÷60,
x=2.5.
答:大约要用2.5小时.
点评:此题考查正比例的意义,即相关联的两个量,如果比值一定,这两个量成正比例关系.
22.成正比例;不成正比例
【详解】试题分析:(1)判断正方形的周长和边长是否成正比例,就看它们是不是比值一定,若比值一定,则成,否则,就不成;
(2)判断正方形的面积和边长是否成正比例,就看它们是不是比值一定,若比值一定,则成,否则,就不成.
解:(1)因为===…==4(一定),
是正方形的周长和边长相对应的两个数的比值一定,符合成正比例的意义,
所以正方形的周长和边长成正比例;
(2)≠…(不一定);
是正方形的面积和边长相对应的两个数的比值不一定,不符合成正比例的意义,
所以正方形的面积和边长不成正比例.
点评:此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
23.320立方厘米
【分析】由题意可知,当铅垂放入容器中,有部分水溢出;长方体容器中下降的水的体积就等于这个铅锤的体积;水面下降了5厘米,也就是说,铅锤的体积,就相当于5+2厘米高的水的体积,根据长方体的体积公式v=Sh,列式解答。
【详解】8×8×(5+2)=448(立方厘米);
答:铅锤的体积是448立方厘米。
24.100×(35%-20%)=15(页)
【详解】略
25.0.32立方米
【分析】把圆木锯成4段,就需要锯4﹣1=3次,每锯一次就多出两个横截面,锯成4段就多了(4﹣1)×2=6个圆木的横截面,再除48,就是这个圆木的底面积,乘圆木的高,就是它的体积。
【详解】48平方分米=0.48平方米
0.48÷[(4﹣1)×2]×4
=0.48÷[3×2]×4
=0.48÷6×4
=0.32(立方米)
答:这根圆木原来的体积是0.32立方米。
【点睛】本题的关键是让学生根据锯的段数,求出增加的底面数,再求出圆木的底面积,然后根据体积公式进行计算。注意要统一单位。
26.圆锥体,50.24
【详解】试题分析:分别以直角三角形的直角边为轴,将三角形旋转一周,得到的是一个圆锥体,有两种情况,分别求出这两个圆锥的体积,进行比较,就可以解决.
解:(1)以3厘米的边为轴旋转一周,可以得到一个圆锥,
体积为:×π×42×3=16π=50.24(立方厘米);
(2)以4厘米的边为轴旋转一周,可以得到一个圆锥,
体积为:×π×32×4=12π=37.68(立方厘米);
答:得到的是一个圆锥体,这个图形的体积是50.24或37.68立方厘米.
故答案为圆锥体,50.24.
点评:此题考查了圆锥的展开图的特点和体积公式的综合应用.
27.打字的个数,打字的时间,速度,正,比值,900,x,60,4.
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答.
解:(1)已知条件里相关联的两种量是打字的个数和打字用的时间.
(2)根据“照这样计算”这句话,说明张倩每分钟打字的速度是一定的.
(3)说明这两种相关联的量成正比例.也就是说这两种量中相对应的两个数的比值一定.
(4)因此用比例知识解答列式为(用x表示所求问题):
900:x=60:4,
60x=900×6,
x=90;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
28.15厘米
【详解】试题分析:根据圆锥的体积公式,V=Sh,得出h=3V÷S,代入数据,即可解答.
解:由题意知,
V锥=Sh,
得:h=3V锥÷S,
=3×80÷16,
=15(厘米).
答:这个圆锥体的高是15厘米.
点评:解答此题的关键是,将圆锥的体积公式进行变形,得出高的求法,代入数据,即可解答.
29.(30-24)÷30
=6÷30
=0.2
=20%
答:黄花比红花少20%.
【详解】先求出黄花比红花少了多少朵,用少的朵数除以红花的朵数,即可求出黄花比红花少百分之几.
30.圆锥的体积是376.8立方厘米,圆柱的体积是1570立方厘米.
【详解】试题分析:圆锥的体积=πr2h,圆柱的体积=πr2h,由此代入数据即可解答.
解:圆锥的体积是:
×3.14×(12÷2)2×10,
=×3.14×36×10,
=3.14×120,
=376.8(立方厘米);
圆柱的体积是:
3.14×(10÷2)2×20,
=3.14×25×20,
=1570(立方厘米);
答:圆锥的体积是376.8立方厘米,圆柱的体积是1570立方厘米.
点评:此题考查了圆柱与圆锥的体积公式的计算应用,熟记公式即可解答.
31.圆柱
【详解】试题分析:将长方形,围绕它的一条长边为轴旋转一周,得到的是圆柱,即以10厘米边为轴旋转,得到的是:高为10厘米,底面半径是4厘米的圆柱体,由此数据利用圆柱的体积公式解答即可.
解:以10厘米边为轴旋转,得到的是:高为10厘米,底面半径是4厘米;
3.14×42×10,
=3.14×16×10,
=502.4(立方厘米);
答:得到的是圆柱体,这个图形的体积是502.4立方厘米.
故答案为圆柱.
点评:解答此题的关键是找出旋转所得到的图形与原图形之间的数据关系,注意常见的旋转体圆柱、圆锥、球.
32.175.84平方厘米
【详解】试题分析:圆柱的侧面积=底面周长×高,可利用圆的周长公式C=πd计算出圆的底面周长,然后再进行计算即可得到答案.
解:3.14×7×8
=21.98×8,
=175.84(平方厘米),
答:圆柱的侧面积为175.84平方厘米.
点评:此题主要考查的是圆的周长公式的应用和圆柱的侧面积的计算方法.
33.a:b=5 表示成正比例,因为这个式子表示a和b的比值一定.
【详解】略
34.36人
【详解】解:设六年级二班共x人,一班共90%x人.
x-90%x=4
x=40
40-4=36(人)
答;六年级一班有36人.
35.87.92.
【详解】试题分析:根据圆柱的表面积=侧面积+2个底面积,即可列式计算.
解:62.8+12.56×2,
=62.8+25.12,
=87.92(平方厘米);
答:它的表面积是87.92平方厘米.
故答案为87.92.
点评:此题主要考查圆柱的表面积的意义及其计算.
36.错误.
【详解】试题分析:圆的周长与半径是两种相关联的量,圆的周长÷半径=2π,2π一定,也就是这两种量的比值一定,所以成正比例;但前提是圆的周长和它半径成正比例;由于本题任意圆的周长与任意半径,所以不成正比例;据此解答.
解:由分析可知:任意圆的周长与任意半径成正比例,说法错误;
点评:此题考查辨识成正比例的量,只要两种相关联的量比值一定,就成正比例.
37.62.8毫升
【详解】试题分析:根据圆柱的体积公式V=sh=πr2h,先求出玻璃杯内药水的体积,由于药水正好是杯内容量的,由此求出杯子的容量,即再加入杯内容量(1﹣)可以把杯子盛满,由此即可求出答案.
解:玻璃杯内药水的体积:3.14×(8÷2)2×5,
=3.14×16×5,
=3.14×80,
=251.2(立方厘米),
加药水的体积:
251.2×(1﹣),
=251.2××,
=62.8(立方厘米),
62.8立方厘米=62.8毫升;
答:再加62.8毫升药水可以把杯子盛满.
点评:主要是利用圆柱的体积公式V=sh=πr2h与基本的数量关系解决问题.
38.三个球的体积之比是2∶8∶11
【分析】假设小球溢出的水量为1个单位,第二次把中球沉入水中是第一次的3倍,说明中球的体积是1+3=4个单位。 第三次把小球和大球一起沉入水中是一次的2.5倍,小球与大球的体积和是4+2.5=6.5个单位,大球的体积是6.5-1=5.5个单位,从而可以求出三个球的体积比。
【详解】假设小球溢出的水量为1个单位,第二次把中球沉入水中是第一次的3倍,
说明中球的体积是1+3=4个单位。 第三次把小球和大球一起沉入水中是一次的2.5倍,
小球与大球的体积和是4+2.5=6.5个单位,
大球的体积是6.5-1=5.5个单位,
三个球的体积之比是∶1∶4∶5.5=2∶8∶11。
答∶三个球的体积之比是∶2∶8∶11。
【点睛】解答此题的主要依据是∶排出的水的体积就等于放入水中的物体的体积。
39.(1)0.6(米)(2) 706.5平方米
【详解】(1)6×3÷(10+9+11)=0.6(米)
(2)157×0.6=94.2(米)
94.2÷3.14÷2=15(米)
152×3.14=706.5(平方米)
40.80厘米
【详解】
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
青岛版六年级数学下册期末专项训练:解答题
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.一个煤堆近似圆锥体,煤堆底面周长是37.68m,高3m,1m3煤重1.4吨,这堆煤大约重多少吨?(得数保留一位小数)
2.用地砖铺设一块地板,用2平方米的地砖,需要25块,那么用5平方米的地砖,需要多少块?
3.王奶奶有5000元钱,准备存入银行5年,年利率为4.02%,五年后王奶奶能得到本息多少元?
4.橙汁罐为圆柱形,底面直径为6厘米,高为11厘米。将24罐橙汁放入箱内,这个箱子的长、宽、高分别是多少厘米
5.新景小学有1300名学生,其中50%是住校生,你知道住校生有多少名吗?
6.下面是张大爷的一-张储蓄存单,他的存款到期时实际可得多少元利息?
中国建设银行(定期)储蓄存单 账号×××××× 币种人民币 金额(大写)五万元 小写¥50000元
存入期 存期 年利率 起息日 到期日
2010年4月1日 5年 4.75% 2010年4月1日 2015年4月1日
7.一个底面直径是4dm的圆柱形木桶,高6dm。这个木桶破损后(如图)最多能盛多少L水?
8.下面是某小学六年级学生的视力情况统计图.近视人数占全年级学生人数的百分之几 视力不良(包括假性近视和近视)的人数占全年级学生人数的百分之几
9.一个竹筒从里面量直径为6厘米,长为10厘米。把大米装至竹筒长的处做米饭,如果每立方厘米大米重3克,这根竹筒里的大米重多少克?
10.2022年第24届冬季奥运会在北京和张家口举办,北京至张家口的距离约是180千米,在一幅冬奥会宣传图上,两地间的图上距离是60厘米。
(1)这幅宣传图的比例尺是多少?
(2)在这幅宣传图上京张高铁全线长58厘米,京张高铁实际全线长多少千米?
11.判断成不成比例.如果成比例,成什么比例
(1)比的后项一定,它的前项和比值.
(2)打一份稿件,每分钟打字的个数和所需要的时间.
(3)强强跳高的高度与他的身高.
12.一家房地产开发商12月份的营业额是5000万元.如果按营业额的5%缴纳营业税,这家房地产开发商应该缴纳营业税多少万元
13.甲数除乙数的商是1.8,那么甲数与乙数的比是多少?
14.甲、乙两城实际距离是1200千米,画在比例尺是1∶30000000的地图上,两地之间的图上距离是多少厘米?
15.如图,宁宁家距书店1000米。
(1)这幅图的比例尺是多少?
(2)宁宁家到学校的实际距离是多少米?
(3)现要在宁宁家南偏西45°方向1500米处建一个体育馆,请在图中画出体育馆的位置。
16.小颖同学看一本书,所用天数和每天需要看的页数情况如表:
每天看的页数/页 300 150 100 75 60 50 …
所用时间/天 1 2 3 4 5 6 …
表中每天看的页数和所用天数的规律是 ;每题要看的页数和看的天数成 比,如果每天看30页,则要 天;如果用了15天,则每天看 页.
17.一个容积为2128立方厘米的瓶子,正着放饮料高度是30厘米,倒着放空余部分的高度为5厘米,你知道瓶中有多少立方厘米的饮料吗?
18.解比例.
(1)
(2)
(3)
(4)
(5)
(6)
19.判断两个量是否成正比例或反比例,说明理由:
每箱木瓜的个数一定,运来木瓜的箱数和木瓜的总个数.
20.一个圆锥体,体积是18立方米,高1.8米.请问这个圆锥的底面积是多少?
21.汽车行驶的时间和路程如下表.
时间/时 1 2 3 _________ 5 _________
路程/km 60 120 _________ 240 _________ 360
(1)完成表格,路程与时间成 比例;
(2)在图中描出表示路程和相应时间的点,然后把它们按顺序连起来.并估计一下行驶150km大约要用 小时.
22.先观察下表,再判断正方形周长和边长成正比例吗?为什么?正方形面积和边长成正比例吗?为什么?
正方形边长/厘米 1 2 3 4 5 6 7 8 …
正方形周长/厘米 4 8 12 16 20 24 28 32 …
正方形的面积/平方厘米 1 4 9 16 25 36 49 64 …
23.用一个底面为边长8厘米的正方形,高为16厘米的长方体容器,测量一个铅锤的体积,容器中装的水距容器口还有2厘米。当铅垂放入容器中,有部分水溢出;当把铅锤取出后,水面比原来下降了5厘米。这个铅锤的体积是多少立方厘米?
24.小萌读一本100页的故事书,第一天读了这本书的20%,第二天读了这本书的35%,第一天比第二天少读多少页
25.把一根4m长的圆木锯成4段短圆木,表面积比原来增加了48dm2,这根圆木原来的体积是多少?
26.以图的直角三角形的一条边为轴,旋转一周,求得到的形体的体积.
27.张倩用电脑练习打字,前4分钟打了60个字,照这样计算,一篇900字的文章一共需要打多长时间?
(1)已知条件里相关联的两种量是 和 .
(2)根据“照这样计算”这句话,说明张倩每分钟打字的 是一定的.
(3)说明这两种相关联的量成 比例.也就是说这两种量中相对应的两个数的 一定.
(4)因此用比例知识解答列式为(用x表示所求问题): ○ = ○ .
28.一个圆锥体的体积是80立方厘米,底面积是16平方厘米,它的高是多少厘米?
29.手工制作课上,六年级二班制作红花30朵,黄花24朵,黄花比红花少百分之几?
30.求下列图形的体积(单位:cm)
31.如图是一个长方形.请你想象一下,以一条长边为轴旋转一周,可以形成一个 .并计算出它的体积.(单位:厘米)
32.圆柱的底面直径是7厘米,高是8厘米,求侧面积.
33.如果把两种相关联的量用a、b表示,你能判断下列哪个式子表示成正比例吗?
a+b=12 a-b=3.8 ab= a:b=5
34.王庄小学六年级一班的学生人数是六年级二班学生人数的90%,六年级一班的人数比六年级二班少4人.六年级一班有多少人
35.一个圆柱的底面积是12.56平方厘米,侧面积是62.8平方厘米,它的表面积是 平方厘米.
36.任意圆的周长与任意半径成正比例. .
37.有一只圆柱形玻璃杯,测得内直径是8厘米,内装药水的深度是5厘米,正好是杯内容量的,再加多少毫升药水可以把杯子盛满?
38.一个容器内已注满水,有大、中、小三个球。第一次把小球沉入水中;第二次把小球取出,把中球沉入水中;第三次取出中球,把小球和大球一起沉入水中,现在知道每次从容器中溢出水量的情况是,第一次是第二次的,第三次是第一次的2.5倍,求三个球的体积之比。
39.小明沿6米长的路走了3次,第一次10步走完,第二次9步走完,第三次11步走完.
(1)他平均一步的长度是多少米
(2)他沿着一个圆形花坛走了一圈,刚好是157步,这个花坛的面积约是多少平方米
40.一个圆柱形的油桶,桶内底面直径是30厘米,高40厘米,桶里盛满汽油.如果把桶里汽油全部倒进一个长方体油箱,油箱还空着.这个油箱的底面积是471平方厘米.这个油箱的高有多少厘米?
《青岛版六年级数学下册期末专项训练:解答题》参考答案
1.158.3吨
【分析】要求这堆煤的重量,先求得煤的体积,煤堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,进一步再求煤的重量,问题得解。
【详解】煤堆的体积:
×3.14×(37.68÷3.14÷2)2×3
=3.14×62
=3.14×36
=113.04(立方米);
煤堆的重量:
113.04×1.4≈158.3(吨);
答:这堆煤约重158.3吨。
【点睛】此题主要考查圆锥的体积计算公式V=r2h,运用公式计算时不要漏乘。
2.10块
【详解】2×25÷5=10(块)
答:用5平方米的地砖,需要10块。
3.6005元
【详解】5000×4.02%×5+5000=6005(元)
答:五年后王奶奶能得到本息6005元。
4.长:36厘米;宽:24厘米;高:11厘米
【分析】根据图片可知,箱子的长是6个橙汁罐底面直径的距离,所用要求这个箱子的长度就是求6个6厘米是多少,用乘法计算;箱子的宽是4个橙汁罐底面直径的距离,所用要求这个箱子的宽度就是求4个6厘米是多少,用乘法计算;箱子的高就是橙汁罐的高度,据此解答。
【详解】长:
宽:
高:11厘米
答:这个箱子的长是36厘米,宽是24厘米,高是11厘米。
【点睛】认真观察给出的图片:充分理解这个箱子的长、宽、高与橙汁罐之间的数量关系。
5.650名
【分析】根据题意,新景小学有1300名学生,其中有50%是住校生,用1300×50%,就是住校生的人数。
【详解】1300×50%=650(名)
答:住校生有650名。
【点睛】本题考查求一个数的百分之几是多少,用乘法。
6.11875元
【分析】根据利息公式:利息=本金×利率×时间,代入数据,即可求出到期的利息。
【详解】50000×4.75%×5
=2375×5
=11875(元)
答:他的存款到期时实际可得11875元。
7.69.08L
【分析】观察图形可知,水桶能盛水的最高高度是6dm-5cm=5.5dm,由此再利用圆柱的容积公式即可解答。
【详解】5cm=0.5dm
3.14×(4÷2)2×(6-0.5)
=3.14×4×5.5
=69.08(dm3)
=69.08(L)
答:这个木桶破损后最多能盛69.08L水。
【点睛】此题主要考查圆柱的容积公式的灵活应用,注意确定水桶的储水高度。
8.29%,59%
【详解】解:1-(30%+41%)=29%
1-41%=59%
答:近视人数占全年级学生人数的29%,视力不良(包括假性近视和近视)的人数占全年级学生人数的59%.
9.847.8克
【分析】先求出竹筒的体积,用竹筒体积的就是大米的体积,用大米的体积乘3,就是大米的重量。
【详解】
=
=
=(克)
答:这根竹筒里的大米重847.8克。
【点睛】重点是求出大米的体积,根据的大米的体积求重量。
10.(1)1∶300000;
(2)174千米。
【分析】(1)根据比例尺的定义,比例尺是图上距离与实际距离的比,把图上距离与实际距离的单元统一一下代入公式即可得解;
(2)根据(1)中得出的比例尺,利用比例的性质即可得解。
【详解】(1)180千米=18000000厘米
60∶18000000=1∶300000
答:这幅宣传图的比例尺是1∶300000。
(2)图上1厘米表示300000厘米,即1厘米表示3千米,
3×58=174(千米)
答:京张高铁实际全线长174千米。
11.(1)成正比例 (2)成反比例 (3)不成比例
【详解】略
12.5000×5%=250(万元)
【详解】略
13.甲:乙=5:9
【分析】甲数除乙数,即乙÷甲=1.8=9/5,由此求出甲乙的比
【详解】甲:乙=1:1.8=5:9
14.4厘米
【分析】这道题是已知比例尺、实际距离,求图上距离,根据图上距离=实际距离×比例尺,解答即可。
【详解】1200千米=120000000厘米
120000000×=4(厘米)
答:两地之间的图上距离是4厘米。
【点睛】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题。
15.(1)1∶50000;
(2)2000米;
(3)见详解
【分析】(1)通过直尺测量,宁宁家到书店的图上距离是2厘米,宁宁家距书店1000米,统一单位后,根据比例尺的意义,比例尺=图上距离∶实际距离,代入数据求出这幅图的比例尺。
(2)经测量,宁宁家到学校的图上距离是4厘米,根据实际距离=图上距离÷比例尺,代入数据即可求出宁宁家到学校的实际距离是多少米。
(3)统一单位后,用实际距离×比例尺=图上距离,求出体育馆和宁宁家两地之间的图上距离,再以宁宁家为观测点,利用地图上的方向“上北下南,左西右东”,根据方向、角度、距离确定体育馆的位置,并在图上标注出来。
【详解】(1)1000米=100000厘米
2∶100000=1∶50000
答:这幅图的比例尺是1∶50000。
(2)4÷
=4×50000
=200000(厘米)
200000厘米=2000米
答:宁宁家到学校的实际距离是2000米。
(3)1500米=150000厘米
150000×=3(厘米)
如图:
【点睛】此题主要考查比例尺的意义以及根据方向、角度、距离确定物体的位置。
16.乘积相等,反,10.20.
【详解】试题分析:表中每天看的页数和所用天数的乘积相等,符合反比例的意义;进而根据每天看的页数和所用天数的乘积相等,列出方程或比例,解答后面的两个问题即可.
解:(1)每天看的页数和所用天数的乘积相等,
所以符合反比例的意义,则每天要看的页数和看的天数成反比例关系;
(2)设如果每天看30页,则要x天看完,由题意得:
30x=50×6,
30x÷30=300÷30,
x=10;
答:如果每天看30页,则要10天看完.
(3)设如果用了15天,则每天看x页,由题意得:
15x=50×6,
15x÷15=300÷15,
x=20;
答:如果用了15天,则每天看20页.
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
17.2128÷(30+5)×30
=2128÷35×30
=60.8×30
=1824(立方厘米)
答:瓶中有1824立方厘米的饮料.
【详解】瓶子的容积可以分为两部分,一部分是饮料部分是一个高30厘米的圆柱体,另一部分是空余部分是一个高5厘米的圆柱体,由此可以求出瓶子的底面积;再根据底面积乘高就可以求出饮料的体积.
18.(1)
(2)
(3)
(4)
(5)
(6)
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积.
【详解】(1)
解:
(2)
解:
(3)
解:
(4)
解:
(5)10:50=x:40
解: 50x=10×40
50x=400
x=8
(6)
解:
19.成反比例.
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:因为:木瓜的总个数÷木瓜的箱数=每箱木瓜的个数(一定),所以运来木瓜的箱数和木瓜的总个数成正比例.
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
20.30平方米
【详解】试题分析:根据圆锥的体积公式:v=sh,s=vh,把数据代入公式解答.
解:181.8,
=18×3÷1.8,
=54÷1.8,
=30(平方米);
答:这个圆柱的底面积是30平方米.
点评:此题主要考查圆锥的体积公式的灵活运用.
21.(1)180,4,300,6.正比例.(2)2.5小时.
【详解】试题分析:(1)因为=60,=60,60是一定的数,代表速度,速度(一定),所以路程和时间成正比例,设要填的数为x,列出比例,求出x的值即可,同样求出其它要填的数;
(2)时间:1小时,路程60千米;时间:2小时,路程120千米;时间:3小时,路程180千米;时间:4小时,路程240千米;时间:5小时,路程300千米;时间:6小时,路程360千米,描出表示路程和相应时间的点,然后把它们按顺序连起来.
速度(一定),所以路程和时间成正比例,设行150千米用x小时,列并解比例即可.
解:(1)因为=60,
=60,
因为60是一定的数,代表速度,
速度(一定),所以路程和时间成正比例.
设要填的数为x,
=,
x=180;
答:3小时行180千米;
设要填的数为y,
=,
60y=240,
60y÷60=240÷60,
y=4;
答:行240千米需要4小时;
设要填的数为a,
=,
a=300;
答:5小时行300千米;
设要填的数为b,
=,
60b=360,
60b÷60=360÷60,
b=6.
答:行360千米需要6小时.
(2)时间:1小时,路程60千米;时间:2小时,路程120千米;时间:3小时,路程180千米;时间:4小时,路程240千米;时间:5小时,路程300千米;时间:6小时,路程360千米,描出表示路程和相应时间的点,然后把它们按顺序连起来.
因为速度一定,路程和时间成正比例,
设大约要用x小时,
=,
60x=150,
60x÷60=150÷60,
x=2.5.
答:大约要用2.5小时.
点评:此题考查正比例的意义,即相关联的两个量,如果比值一定,这两个量成正比例关系.
22.成正比例;不成正比例
【详解】试题分析:(1)判断正方形的周长和边长是否成正比例,就看它们是不是比值一定,若比值一定,则成,否则,就不成;
(2)判断正方形的面积和边长是否成正比例,就看它们是不是比值一定,若比值一定,则成,否则,就不成.
解:(1)因为===…==4(一定),
是正方形的周长和边长相对应的两个数的比值一定,符合成正比例的意义,
所以正方形的周长和边长成正比例;
(2)≠…(不一定);
是正方形的面积和边长相对应的两个数的比值不一定,不符合成正比例的意义,
所以正方形的面积和边长不成正比例.
点评:此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
23.320立方厘米
【分析】由题意可知,当铅垂放入容器中,有部分水溢出;长方体容器中下降的水的体积就等于这个铅锤的体积;水面下降了5厘米,也就是说,铅锤的体积,就相当于5+2厘米高的水的体积,根据长方体的体积公式v=Sh,列式解答。
【详解】8×8×(5+2)=448(立方厘米);
答:铅锤的体积是448立方厘米。
24.100×(35%-20%)=15(页)
【详解】略
25.0.32立方米
【分析】把圆木锯成4段,就需要锯4﹣1=3次,每锯一次就多出两个横截面,锯成4段就多了(4﹣1)×2=6个圆木的横截面,再除48,就是这个圆木的底面积,乘圆木的高,就是它的体积。
【详解】48平方分米=0.48平方米
0.48÷[(4﹣1)×2]×4
=0.48÷[3×2]×4
=0.48÷6×4
=0.32(立方米)
答:这根圆木原来的体积是0.32立方米。
【点睛】本题的关键是让学生根据锯的段数,求出增加的底面数,再求出圆木的底面积,然后根据体积公式进行计算。注意要统一单位。
26.圆锥体,50.24
【详解】试题分析:分别以直角三角形的直角边为轴,将三角形旋转一周,得到的是一个圆锥体,有两种情况,分别求出这两个圆锥的体积,进行比较,就可以解决.
解:(1)以3厘米的边为轴旋转一周,可以得到一个圆锥,
体积为:×π×42×3=16π=50.24(立方厘米);
(2)以4厘米的边为轴旋转一周,可以得到一个圆锥,
体积为:×π×32×4=12π=37.68(立方厘米);
答:得到的是一个圆锥体,这个图形的体积是50.24或37.68立方厘米.
故答案为圆锥体,50.24.
点评:此题考查了圆锥的展开图的特点和体积公式的综合应用.
27.打字的个数,打字的时间,速度,正,比值,900,x,60,4.
【详解】试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答.
解:(1)已知条件里相关联的两种量是打字的个数和打字用的时间.
(2)根据“照这样计算”这句话,说明张倩每分钟打字的速度是一定的.
(3)说明这两种相关联的量成正比例.也就是说这两种量中相对应的两个数的比值一定.
(4)因此用比例知识解答列式为(用x表示所求问题):
900:x=60:4,
60x=900×6,
x=90;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
28.15厘米
【详解】试题分析:根据圆锥的体积公式,V=Sh,得出h=3V÷S,代入数据,即可解答.
解:由题意知,
V锥=Sh,
得:h=3V锥÷S,
=3×80÷16,
=15(厘米).
答:这个圆锥体的高是15厘米.
点评:解答此题的关键是,将圆锥的体积公式进行变形,得出高的求法,代入数据,即可解答.
29.(30-24)÷30
=6÷30
=0.2
=20%
答:黄花比红花少20%.
【详解】先求出黄花比红花少了多少朵,用少的朵数除以红花的朵数,即可求出黄花比红花少百分之几.
30.圆锥的体积是376.8立方厘米,圆柱的体积是1570立方厘米.
【详解】试题分析:圆锥的体积=πr2h,圆柱的体积=πr2h,由此代入数据即可解答.
解:圆锥的体积是:
×3.14×(12÷2)2×10,
=×3.14×36×10,
=3.14×120,
=376.8(立方厘米);
圆柱的体积是:
3.14×(10÷2)2×20,
=3.14×25×20,
=1570(立方厘米);
答:圆锥的体积是376.8立方厘米,圆柱的体积是1570立方厘米.
点评:此题考查了圆柱与圆锥的体积公式的计算应用,熟记公式即可解答.
31.圆柱
【详解】试题分析:将长方形,围绕它的一条长边为轴旋转一周,得到的是圆柱,即以10厘米边为轴旋转,得到的是:高为10厘米,底面半径是4厘米的圆柱体,由此数据利用圆柱的体积公式解答即可.
解:以10厘米边为轴旋转,得到的是:高为10厘米,底面半径是4厘米;
3.14×42×10,
=3.14×16×10,
=502.4(立方厘米);
答:得到的是圆柱体,这个图形的体积是502.4立方厘米.
故答案为圆柱.
点评:解答此题的关键是找出旋转所得到的图形与原图形之间的数据关系,注意常见的旋转体圆柱、圆锥、球.
32.175.84平方厘米
【详解】试题分析:圆柱的侧面积=底面周长×高,可利用圆的周长公式C=πd计算出圆的底面周长,然后再进行计算即可得到答案.
解:3.14×7×8
=21.98×8,
=175.84(平方厘米),
答:圆柱的侧面积为175.84平方厘米.
点评:此题主要考查的是圆的周长公式的应用和圆柱的侧面积的计算方法.
33.a:b=5 表示成正比例,因为这个式子表示a和b的比值一定.
【详解】略
34.36人
【详解】解:设六年级二班共x人,一班共90%x人.
x-90%x=4
x=40
40-4=36(人)
答;六年级一班有36人.
35.87.92.
【详解】试题分析:根据圆柱的表面积=侧面积+2个底面积,即可列式计算.
解:62.8+12.56×2,
=62.8+25.12,
=87.92(平方厘米);
答:它的表面积是87.92平方厘米.
故答案为87.92.
点评:此题主要考查圆柱的表面积的意义及其计算.
36.错误.
【详解】试题分析:圆的周长与半径是两种相关联的量,圆的周长÷半径=2π,2π一定,也就是这两种量的比值一定,所以成正比例;但前提是圆的周长和它半径成正比例;由于本题任意圆的周长与任意半径,所以不成正比例;据此解答.
解:由分析可知:任意圆的周长与任意半径成正比例,说法错误;
点评:此题考查辨识成正比例的量,只要两种相关联的量比值一定,就成正比例.
37.62.8毫升
【详解】试题分析:根据圆柱的体积公式V=sh=πr2h,先求出玻璃杯内药水的体积,由于药水正好是杯内容量的,由此求出杯子的容量,即再加入杯内容量(1﹣)可以把杯子盛满,由此即可求出答案.
解:玻璃杯内药水的体积:3.14×(8÷2)2×5,
=3.14×16×5,
=3.14×80,
=251.2(立方厘米),
加药水的体积:
251.2×(1﹣),
=251.2××,
=62.8(立方厘米),
62.8立方厘米=62.8毫升;
答:再加62.8毫升药水可以把杯子盛满.
点评:主要是利用圆柱的体积公式V=sh=πr2h与基本的数量关系解决问题.
38.三个球的体积之比是2∶8∶11
【分析】假设小球溢出的水量为1个单位,第二次把中球沉入水中是第一次的3倍,说明中球的体积是1+3=4个单位。 第三次把小球和大球一起沉入水中是一次的2.5倍,小球与大球的体积和是4+2.5=6.5个单位,大球的体积是6.5-1=5.5个单位,从而可以求出三个球的体积比。
【详解】假设小球溢出的水量为1个单位,第二次把中球沉入水中是第一次的3倍,
说明中球的体积是1+3=4个单位。 第三次把小球和大球一起沉入水中是一次的2.5倍,
小球与大球的体积和是4+2.5=6.5个单位,
大球的体积是6.5-1=5.5个单位,
三个球的体积之比是∶1∶4∶5.5=2∶8∶11。
答∶三个球的体积之比是∶2∶8∶11。
【点睛】解答此题的主要依据是∶排出的水的体积就等于放入水中的物体的体积。
39.(1)0.6(米)(2) 706.5平方米
【详解】(1)6×3÷(10+9+11)=0.6(米)
(2)157×0.6=94.2(米)
94.2÷3.14÷2=15(米)
152×3.14=706.5(平方米)
40.80厘米
【详解】
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
