【核心考点集训】数学广角《鸡兔同笼》课件(共15张PPT)--人教版四年级下册数学
文档属性
| 名称 | 【核心考点集训】数学广角《鸡兔同笼》课件(共15张PPT)--人教版四年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 425.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
人教版 数学 四年级 下册
鸡兔同笼
知识归纳
模块一:知识点复习
知识点:鸡兔同笼问题
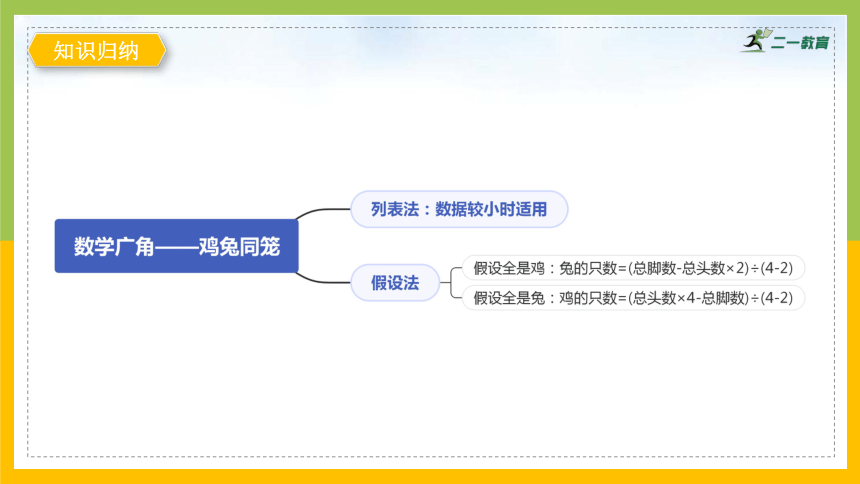
知识梳理
1.解答“鸡兔同笼”问题,可以用猜测、列表、假设等多种方法。
其中假设法的解答过程是:
假设——计算——推理——解答
2.当题中所给数据比较大时,不宜采用猜测、列表法,采用假设法解决问题比较简便。
模块二:例题讲解
模块二:例题讲解
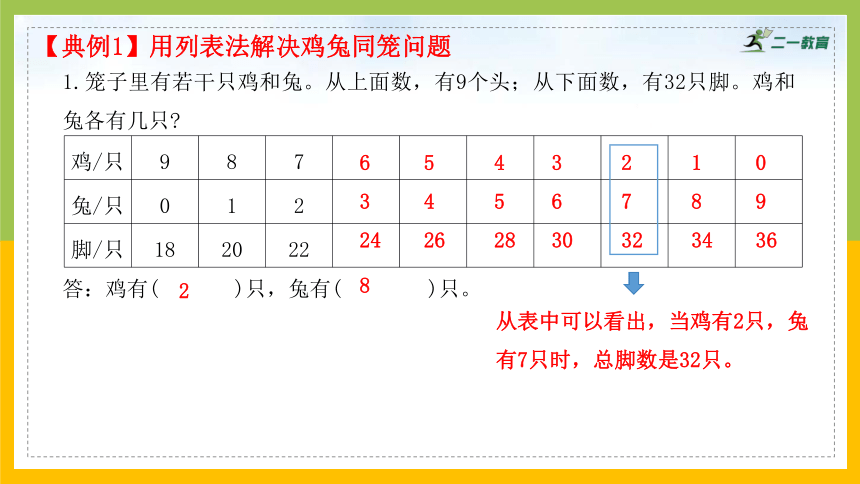
【典例1】用列表法解决鸡兔同笼问题
从表中可以看出,当鸡有2只,兔有7只时,总脚数是32只。
1.笼子里有若干只鸡和兔。从上面数,有9个头;从下面数,有32只脚。鸡和兔各有几只
鸡/只 9 8 7
兔/只 0 1 2
脚/只 18 20 22
答:鸡有( )只,兔有( )只。
6
3
24
5
4
26
4
5
28
3
6
30
2
7
32
1
8
34
0
9
36
2
8
【典例2】用假设法解决鸡兔同笼问题
分析:假设全是乙款灯笼串。
解答:甲:(46-16×2)÷(4-2)=7(串)
乙:16-7=9(串)
莲花湖公园里挂有甲、乙两款灯笼串,每款灯笼串都是由大灯笼和小灯笼组合而成的(如图)。大灯笼共有16个,小灯笼共有46个。甲、乙两款灯笼串各有多少串
小灯笼总个数:2×16=32(个)
实际小灯笼总个数:46个
少了46—32=14(个)
每把1串甲款灯笼串看成乙款灯笼串就少2个小灯笼
甲款:
14÷2=7(串)
乙款:
16-7=9(串)
【典例3】解决“倒扣型”鸡兔同笼问题
分析:假设8道题全答对,则一共应得8×10=80(分),
与实际得分相差80-64=16(分),说明在答题过程中有答错的题。
答对一题加10分,答错一题扣6分,中间相差10+6=16(分)。
学校举办“我是环保小卫士”知识抢答赛,规则如下:答对一道加10分,答错一道扣6分。婷婷共抢答8道题,最后得分64分。她答对了多少道题
答错的题=总共的分数差÷一题的分数差
解答:答错:(10×8-64)÷(10+6)=1(道)
答对:8-1=7(道)
【典例4】假设法或分组法解决复杂的鸡兔同笼变式题
鸡和兔共有100只,鸡的脚比兔的脚多80只。鸡和兔各有多少只
分析:假设法
假设全是鸡,那么总脚数是200只,这时兔的脚数为0,鸡脚比兔脚多200只。
实际鸡脚比兔脚多80只。
假设的鸡、兔脚数差比实际的鸡、兔脚数差多200-80=120(只)。
解答:兔:(100×2-80)÷(4+2)=20(只)
鸡:100-20=80(只)
【典例4】假设法或分组法解决复杂的鸡兔同笼变式题
鸡和兔共有100只,鸡的脚比兔的脚多80只。鸡和兔各有多少只
分析:分组法
去掉鸡比兔多的80只脚。
剩下的鸡和兔的脚数相等。
鸡和兔就剩下:
100-80÷2=60(只)
把2只鸡和1只兔看作1组,每组鸡和兔的脚数都相等
解答: 兔:(100—80÷2)÷(2+1)=20(只)
鸡:100-20=80(只)
模块三:完成变式训练
1.某团队共有54人,共租了10只船。每只大船坐6人,每只小船坐4人,且所有的船刚好坐满。大船和小船各租了多少只
大船/只
小船/只
总人数
答:大船租了( )只,小船租了( )只。
10
0
60
9
1
58
8
2
56
7
3
54
6
4
52
7
3
2.李老师组织36名学生去烈士陵园进行祭奠扫墓活动。李老师献了22朵白花,男同学每人献了6朵白花,女同学每人献了9朵白花,一共献了298朵白花。男同学有多少人参加了这次活动
解答:298-22=276(朵)
(36×9-276)÷(9-6)=16(人)
答:男同学有16人参加了这次活动。
3.某快递公司给客户运送500个玻璃杯。双方商定:每个运费是2元,如果快递公司损坏一个,那么不但得不到运费,还要给客户赔偿8元,最后结算时快递公司共得运费950元。快递公司损坏了多少个玻璃杯
解答:(2×500-950)÷(2+8)=5(个)
答:快递公司损坏了5个玻璃杯。
4.兔爸爸和兔哥哥采蘑菇。兔爸爸先采了2天,后来兔爸爸和兔哥哥各采了7天,一共采了319朵蘑菇。已知兔爸爸比兔哥哥每天多采7朵蘑菇,兔爸爸和兔哥哥每天分别采多少朵蘑菇
解答:2+7+7=16(天)
319+7×7=368(朵) 爸爸:368÷16=23(朵) 哥哥:23-7=16(朵)
答:兔爸爸每天采23朵蘑菇,兔哥哥每天采16朵蘑菇。
人教版 数学 四年级 下册
鸡兔同笼
知识归纳
模块一:知识点复习
知识点:鸡兔同笼问题
知识梳理
1.解答“鸡兔同笼”问题,可以用猜测、列表、假设等多种方法。
其中假设法的解答过程是:
假设——计算——推理——解答
2.当题中所给数据比较大时,不宜采用猜测、列表法,采用假设法解决问题比较简便。
模块二:例题讲解
模块二:例题讲解
【典例1】用列表法解决鸡兔同笼问题
从表中可以看出,当鸡有2只,兔有7只时,总脚数是32只。
1.笼子里有若干只鸡和兔。从上面数,有9个头;从下面数,有32只脚。鸡和兔各有几只
鸡/只 9 8 7
兔/只 0 1 2
脚/只 18 20 22
答:鸡有( )只,兔有( )只。
6
3
24
5
4
26
4
5
28
3
6
30
2
7
32
1
8
34
0
9
36
2
8
【典例2】用假设法解决鸡兔同笼问题
分析:假设全是乙款灯笼串。
解答:甲:(46-16×2)÷(4-2)=7(串)
乙:16-7=9(串)
莲花湖公园里挂有甲、乙两款灯笼串,每款灯笼串都是由大灯笼和小灯笼组合而成的(如图)。大灯笼共有16个,小灯笼共有46个。甲、乙两款灯笼串各有多少串
小灯笼总个数:2×16=32(个)
实际小灯笼总个数:46个
少了46—32=14(个)
每把1串甲款灯笼串看成乙款灯笼串就少2个小灯笼
甲款:
14÷2=7(串)
乙款:
16-7=9(串)
【典例3】解决“倒扣型”鸡兔同笼问题
分析:假设8道题全答对,则一共应得8×10=80(分),
与实际得分相差80-64=16(分),说明在答题过程中有答错的题。
答对一题加10分,答错一题扣6分,中间相差10+6=16(分)。
学校举办“我是环保小卫士”知识抢答赛,规则如下:答对一道加10分,答错一道扣6分。婷婷共抢答8道题,最后得分64分。她答对了多少道题
答错的题=总共的分数差÷一题的分数差
解答:答错:(10×8-64)÷(10+6)=1(道)
答对:8-1=7(道)
【典例4】假设法或分组法解决复杂的鸡兔同笼变式题
鸡和兔共有100只,鸡的脚比兔的脚多80只。鸡和兔各有多少只
分析:假设法
假设全是鸡,那么总脚数是200只,这时兔的脚数为0,鸡脚比兔脚多200只。
实际鸡脚比兔脚多80只。
假设的鸡、兔脚数差比实际的鸡、兔脚数差多200-80=120(只)。
解答:兔:(100×2-80)÷(4+2)=20(只)
鸡:100-20=80(只)
【典例4】假设法或分组法解决复杂的鸡兔同笼变式题
鸡和兔共有100只,鸡的脚比兔的脚多80只。鸡和兔各有多少只
分析:分组法
去掉鸡比兔多的80只脚。
剩下的鸡和兔的脚数相等。
鸡和兔就剩下:
100-80÷2=60(只)
把2只鸡和1只兔看作1组,每组鸡和兔的脚数都相等
解答: 兔:(100—80÷2)÷(2+1)=20(只)
鸡:100-20=80(只)
模块三:完成变式训练
1.某团队共有54人,共租了10只船。每只大船坐6人,每只小船坐4人,且所有的船刚好坐满。大船和小船各租了多少只
大船/只
小船/只
总人数
答:大船租了( )只,小船租了( )只。
10
0
60
9
1
58
8
2
56
7
3
54
6
4
52
7
3
2.李老师组织36名学生去烈士陵园进行祭奠扫墓活动。李老师献了22朵白花,男同学每人献了6朵白花,女同学每人献了9朵白花,一共献了298朵白花。男同学有多少人参加了这次活动
解答:298-22=276(朵)
(36×9-276)÷(9-6)=16(人)
答:男同学有16人参加了这次活动。
3.某快递公司给客户运送500个玻璃杯。双方商定:每个运费是2元,如果快递公司损坏一个,那么不但得不到运费,还要给客户赔偿8元,最后结算时快递公司共得运费950元。快递公司损坏了多少个玻璃杯
解答:(2×500-950)÷(2+8)=5(个)
答:快递公司损坏了5个玻璃杯。
4.兔爸爸和兔哥哥采蘑菇。兔爸爸先采了2天,后来兔爸爸和兔哥哥各采了7天,一共采了319朵蘑菇。已知兔爸爸比兔哥哥每天多采7朵蘑菇,兔爸爸和兔哥哥每天分别采多少朵蘑菇
解答:2+7+7=16(天)
319+7×7=368(朵) 爸爸:368÷16=23(朵) 哥哥:23-7=16(朵)
答:兔爸爸每天采23朵蘑菇,兔哥哥每天采16朵蘑菇。
