期末复习卷-2024-2025学年数学五年级下册苏教版(含解析)
文档属性
| 名称 | 期末复习卷-2024-2025学年数学五年级下册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 849.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末复习卷-2024-2025学年数学五年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面计数器表示的数中,( )是3的倍数。
A. B. C. D.
2.下面四句话中,描述圆半径长度的是( )。
A.画圆时圆规两脚间的距离是2厘米 B.圆形纸片对折一次后折痕长5厘米
C.摩天轮转动一周约转过62.8米 D.喷水器旋转一周喷灌78.5平方米
3.甲、乙、丙、丁四个数在直线上的位置如下图所示,( )可能是。
A.甲 B.乙 C.丙 D.丁
4.下列式子中,( )是方程。
A.5 B.2+7=17 C.-6>4 D.16÷8=2
5.公园管理处要在一棵大榕树周围安装围树环形座椅(见示意图)。他们用一根绳子绕树干10圈,量得结果是18.84米。应选购下面( )种座椅。
A.内圆直径50厘米,外圆直径130厘米 B.内圆直径60厘米,外圆直径1.4米
C.内圆直径1米,外圆直径1.8米 D.内圆直径6米,外圆直径6.8米
6.下面四个选项中,最适合用复式折线统计图的是( )。
A.某病人一天体温变化情况 B.2023年仪征市各小学人数
C.刘辰家去年各项支出情况 D.新华书店两种图书上半年销售变化情况
7.电脑爱好者于飞设计了一个计算程序:“输入一个数→乘3→加6→输出结果”,他输入一个数后,输出结果是36,则于飞输入的数是( )。
A.10 B.12 C.14 D.114
8.某同学从家出发,按一定的速度步行去学校,途中天气有变,将要下雨,他便跑步去学校。下面各图中,能正确地表示出他行进的路程与时间关系的是( )。
A. B.
C. D.
二、填空题
9.小军用下图表示A、B两个数的公倍数,那么A、B两个数分别是( )和( ),它们的最小公倍数是( )。
10.如果2.8+x=4.3,那么x-0.42的值是( ),x÷15=( )。
11.一个最简分数,分子扩大为原来的2倍、分母缩小为原来的后等于3,这个分数原来是( )。
12.一个挂钟的时针长20厘米,这根时针走了12小时,它的尖端走了( )厘米。
13.若3个连续的奇数中,中间的一个数是a,则最小的数是( ),这三个数的和是( )。如果这三个数的和是45,那么最大的数是( )。
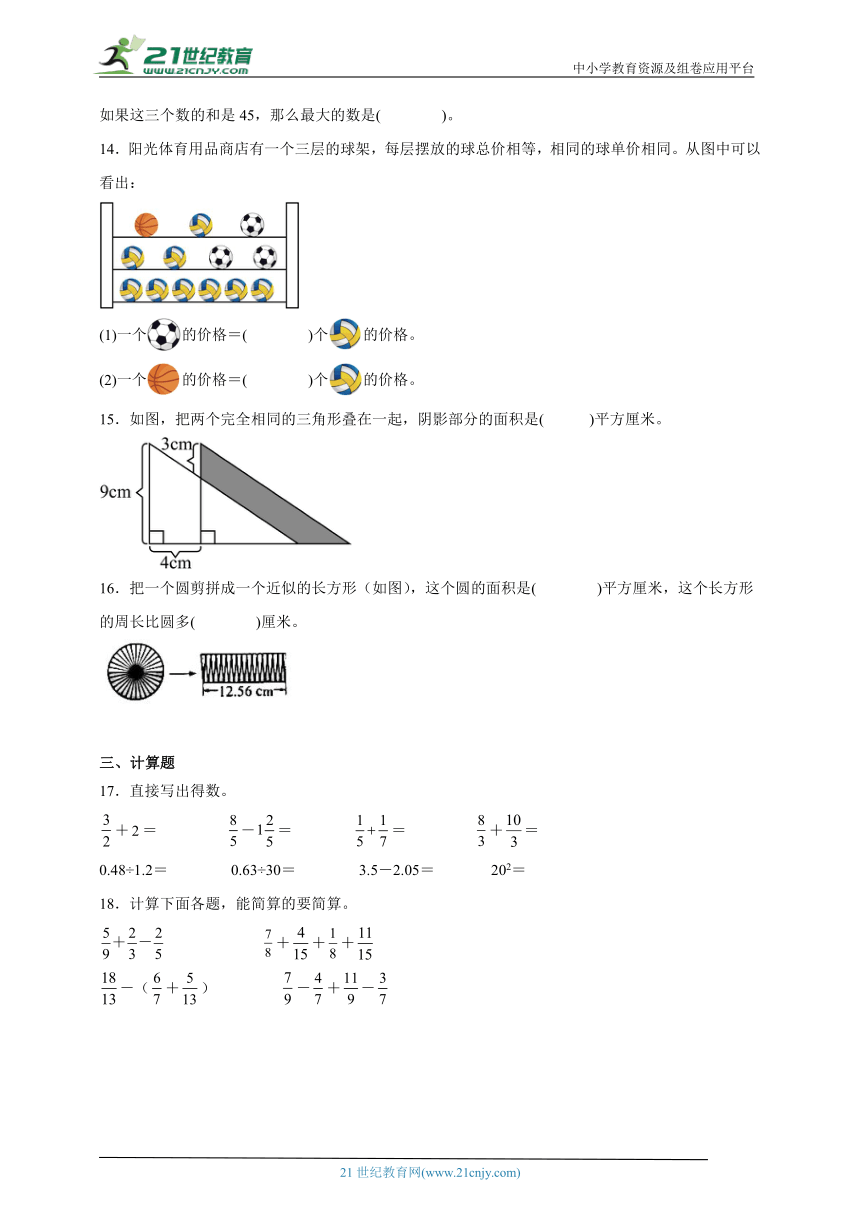
14.阳光体育用品商店有一个三层的球架,每层摆放的球总价相等,相同的球单价相同。从图中可以看出:
(1)一个的价格=( )个的价格。
(2)一个的价格=( )个的价格。
15.如图,把两个完全相同的三角形叠在一起,阴影部分的面积是( )平方厘米。
16.把一个圆剪拼成一个近似的长方形(如图),这个圆的面积是( )平方厘米,这个长方形的周长比圆多( )厘米。
三、计算题
17.直接写出得数。
+= -= = +=
0.48÷1.2= 0.63÷30= 3.5-2.05= 202=
18.计算下面各题,能简算的要简算。
+++
-(+) -+-
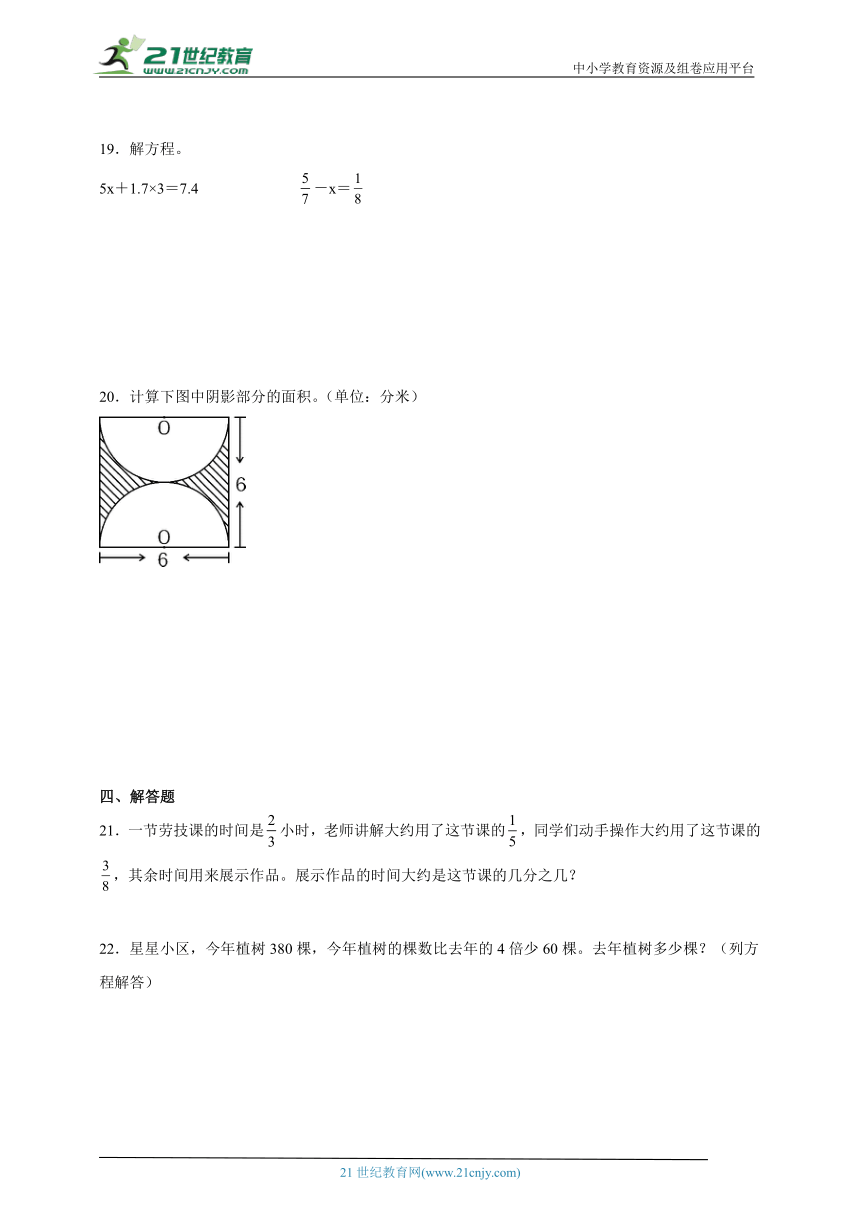
19.解方程。
5x+1.7×3=7.4 -x=
20.计算下图中阴影部分的面积。(单位:分米)
四、解答题
21.一节劳技课的时间是小时,老师讲解大约用了这节课的,同学们动手操作大约用了这节课的,其余时间用来展示作品。展示作品的时间大约是这节课的几分之几?
22.星星小区,今年植树380棵,今年植树的棵数比去年的4倍少60棵。去年植树多少棵?(列方程解答)
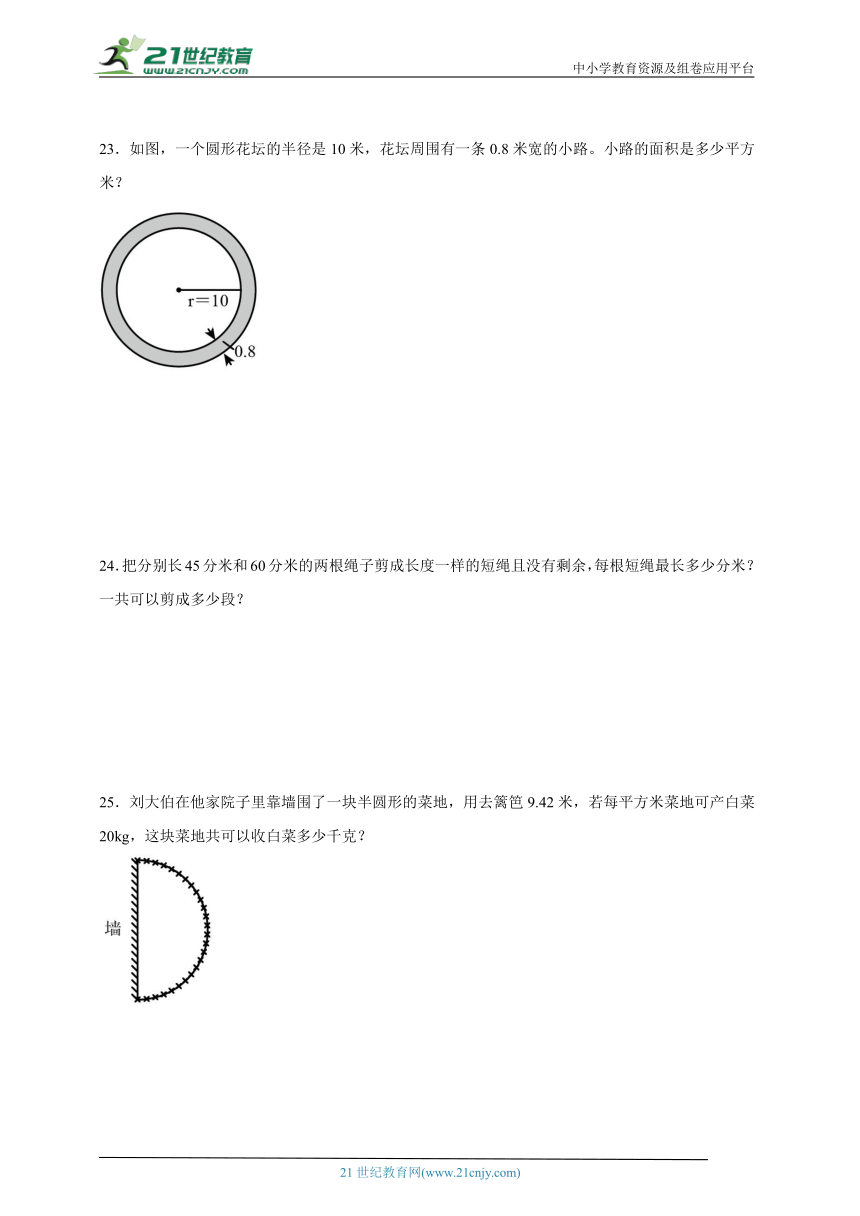
23.如图,一个圆形花坛的半径是10米,花坛周围有一条0.8米宽的小路。小路的面积是多少平方米?
24.把分别长45分米和60分米的两根绳子剪成长度一样的短绳且没有剩余,每根短绳最长多少分米?一共可以剪成多少段?
25.刘大伯在他家院子里靠墙围了一块半圆形的菜地,用去篱笆9.42米,若每平方米菜地可产白菜20kg,这块菜地共可以收白菜多少千克?
26.统计分析。
同学们都知道龟兔赛跑的故事吧?下面是表示龟兔赛跑比赛情况的折线统计图,请你认真读图,回答问题。
(1)实线、虚线分别表示哪种动物?实线表示( ),虚线表示( )。
(2)兔子出发( )分钟后开始睡觉,睡了( )分钟。
(3)乌龟平均每分钟爬行多少米?(得数保留一位小数)
《期末复习卷-2024-2025学年数学五年级下册苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A C B C D A C
1.D
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数;据此解答。
【详解】A.计数器表示121,1+2+1=4,4不是3的倍数,则121不是3的倍数;
B.计数器表示304,3+0+4=7,7不是3的倍数,则304不是3的倍数;
C.计数器表示35,3+5=8,8不是3的倍数,则35不是3的倍数;
D.计数器表示243,2+4+3=9,9是3的倍数,则243是3的倍数;
故答案为:D
【点睛】本题主要考查3的倍数特征,熟练应用3的倍数特征是解题的关键。
2.A
【分析】根据对圆的半径、直径、周长、面积的认识逐项分析即可。
【详解】A.画圆时圆规两脚间的距离是2厘米,而圆规两脚间的距离就是原的半径,该选项描述的是圆半径的长度;
B.圆形纸片对折一次后折痕是圆的直径,所以圆形纸片对折一次后折痕长5厘米描述圆直径的长度;
C.摩天轮转动一周是圆的周长,所以摩天轮转动一周约转过62.8米描述圆周长;
D.喷水器旋转一周扫过的面积是圆的面积;所以喷水器旋转一周喷灌78.5平方米描述圆的面积。
故答案为:A
【点睛】本题考查对圆的半径、直径、周长、面积的认识。
3.C
【分析】化为带分数是,1<<2,且距离2比较近;据此解答。
【详解】=
在1和2之间,靠近2。结合图示可知:丙可能是。
故答案为:C
【点睛】本题主要考查假分数化带分数的方法。
4.B
【分析】含有未知数的等式叫做方程;据此解答。
【详解】A.5,含有未知数,但不是等式,所以不是方程;
B.2+7=17,既含有未知数,又是等式,所以是方程;
C.-6>4,含有未知数,但不是等式,所以不是方程;
D.16÷8=2,是等式,但不含未知数,所以不是方程。
故答案为:B
【点睛】本题考查方程的意义及应用,明确方程必须满足两个条件:一是含有未知数,二是等式。
5.C
【分析】绳子长度÷10=大榕树周长,根据圆的直径=周长÷圆周率,求出榕树直径,安装的环形座椅的内圆应该比树的周长大一点,给大榕树成长的空间,据此选择。
【详解】18.84÷10=1.884(米)
1.884÷3.14=0.6(米)=60(厘米)
A.直径小于大榕树直径,安装不上,排除;
B.直径刚好等于大榕树直径,没有留出一定距离,排除;
C.直径大于大榕树直径一些,可以;
D.直径大于大榕树直径太多,不合适,排除。
应选购内圆直径1米,外圆直径1.8米种座椅。
故答案为:C
【点睛】关键是掌握并灵活运用圆的周长公式。
6.D
【分析】条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
【详解】A.某病人一天体温变化情况,最适合用单式折线统计图;
B.2023年仪征市各小学人数,最适合用单式条形统计图;
C.刘辰家去年各项支出情况,最适合用单式条形统计图;
D.新华书店两种图书上半年销售变化情况,最适合用复式折线统计图。
最适合用复式折线统计图的是新华书店两种图书上半年销售变化情况。
故答案为:D
【点睛】关键是熟悉条形统计图和折线统计图的特点,根据统计图的特点确定最合适的统计图。
7.A
【分析】设于飞输入的数是x,根据于飞所设计的程序可列出方程3x+6=36,再根据等式的性质解方程即可求出于飞所输入的数。
【详解】解:设于飞输入的数是x。
3x+6=36
3x+6-6=36-6
3x=30
3x÷3=30÷3
x=10
所以于飞输入的数是10。
故答案为:A
【点睛】列方程解决问题时,把所求的未知数用x表示,未知数参与列式,把算术法的逆向思维转变成列方程的顺向思维来思考。
8.C
【分析】根据某学生的行驶情况,先步行(慢速行驶),再跑步(快速行驶),而图象表示行进的路程与时间的关系,可知先平缓后变陡,由此即可作出判断。
【详解】A.,观察图意可知,速度保持不变,不符合题意;
B.,先陡后相对平缓,即;先快后慢,不符合题意;
C.,先相对平缓后变陡,即先慢后快,描述了某同学行驶的过程,符合题意。
D.,先匀速行驶,再停止不变,不符合题意。
故答案为:C
【点睛】本题主要考查动点问题的图象,关键在于读懂图象所表示的意思。
9. 4 6 12
【分析】一个数最小的倍数是它本身,据此找到A、B两个数;A、B两个数的最小公倍数是它们的公倍数中最小的那一个,据此解答即可。
【详解】观察集合圈可知,A、B两个数分别是4和6,它们的最小公倍数是12。
【点睛】本题考查公倍数与最小公倍数,解答本题的关键是掌握公倍数与最小公倍数的概念。
10. 1.08 0.1
【分析】先根据等式的性质解方程2.8+x=4.3,等式左右两边同时减2.8,求出未知数x的值,然后代入求值。据此解答即可。
【详解】2.8+x=4.3
解:2.8+x-2.8=4.3-2.8
x=1.5
把x=1.5代入x-0.42中,得
x-0.42=1.5-0.42=1.08
把x=1.5代入x÷15中,得
x÷15=1.5÷15=0.1
所以,x-0.42的值是1.08,x÷15=0.1
【点睛】此题考查了根据等式的性质解方程,以及代入求值。
11.
【分析】根据题意,将这个结果倒推求解,从结果出发,逐步向前一步一步推理。在向前推理的过程中,每一步运算都是原来运算的逆运算。即:把3化成假分数,再分母乘5,分子除以2,再根据分数的基本性质,化成分子和分母只有公因数1的最简分数,即可推出原来的分数。
【详解】根据分析可得:
一个最简分数,分子扩大为原来的2倍、分母缩小为原来的后等于3,这个分数原来是。
12.125.6
【分析】时针走了12小时,就是时针走出挂钟的一圈;求尖端走的长度,就是求半径是20厘米圆的周长,根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】3.14×20×2
=62.8×2
=125.6(厘米)
一个挂钟的时针长20厘米,这根时针走了12小时,它的尖端走了125.6厘米。
13. a-2 3a 17
【分析】相邻的奇数相差2,中间数-2=最小的奇数;用中间数+2=最大的奇数,再把它们相加,即可求出这三个数的和;再用45÷3,求出中间数,再加上2,即可求出最大的数。
【详解】最小的数是(a-2);
最大的数是(a+2)
a-2+a+a+2=3a
45÷3+2
=15+2
=17
若3个连续的奇数中,中间的一个数是a,则最小的数是a-2,这三个数的和是3a。如果这三个数的和是45,那么最大的数是17。
14.(1)2
(2)3
【分析】
(1)从图中可知,第一层球架上有6个,第二层球架上有2个和2个;因为每层摆放的球总价相等,那么6个的价格=2个的价格+2个的价格,运用等式的性质得出的价格和的价格的关系。
(2)从图中可知,第三层球架上有1个、1个和1个,根据上一题的答案,用2个替换掉1个,根据第三层球架上球的价格=第一层球架上球的价格,据此得出等式,再运用等式的性质得出一个的价格相当于几个的价格。
等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
【详解】(1)
6个的价格=2个的价格+2个的价格
等式两边同时减去2个的价格,得:4个的价格=2个的价格;
等式两边同时除以2,得:2个的价格=1个的价格;
所以,一个的价格=2个的价格。
(2)
1个的价格+1个的价格+1个的价格=6个的价格
把“一个的价格=2个的价格”代入式子中,得:
1个的价格+1个的价格+2个的价格=6个的价格
即1个的价格+3个的价格=6个的价格
等式两边同时减去3个的价格,得:1个的价格=3个的价格;
所以,一个的价格=3个的价钱。
15.30
【分析】从图中分析可知,是将三角形向右平移了4厘米,即阴影部分的面积可以转化为左边梯形的面积。再根据梯形的面积=(上底+下底)×高÷2,得出阴影部分的面积。
【详解】9-3=6(厘米)
(6+9)×4÷2
=15×4÷2
=15×2
=30(平方厘米)
则阴影部分的面积是30平方厘米。
16. 50.24 8
【分析】把一个圆剪拼成一个近似的长方形,则长方形的长相当于圆周长的一半,宽相当于圆的半径;已知长方形的长为12.56厘米,则这个圆周长的一半是12.56厘米,代入圆的周长公式:C=2πr,求出圆的半径,再将半径代入圆的面积公式:S=πr2计算即可求出面积;拼成的长方形的周长比圆的周长多两条半径,用求出的半径乘2即可求出这个长方形的周长比圆多多少厘米;据此解答。
【详解】半径:12.56×2÷3.14÷2
=25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
4×2=8(厘米)
把一个圆剪拼成一个近似的长方形(如图),这个圆的面积是50.24平方厘米,这个长方形的周长比圆多8厘米。
17.;;;6;
0.4;0.021;1.45;400
【详解】略
18.;2;;1
【分析】+-,按照运算顺序,先计算加法,再计算减法;
+++,根据加法交换律,原式化为:+++,再根据加法结合律,原式化为:(+)+(+),再进行计算;
-(+),根据减法性质,原式化为:--,再根据加法交换律,原式化为:--,再进行计算;
-+-,根据加法交换律,原式化为:+--,再根据加法结合律和减法性质,原式化为:(+)-(+),再进行计算。
【详解】+-
=+-
=-
=-
=
+++
=+++
=(+)+(+)
=1+1
=2
-(+)
=--
=--
=1-
=
-+-
=+--
=(+)-(+)
=2-1
=1
19.x=0.46;x=
【分析】5x+1.7×3=7.4,先计算出1.7×3的积,再根据等式的性质1,方程两边同时减去1.7×3的积,再根据等式的性质2,方程两边同时除以5即可;
-x=,根据等式的性质1,方程两边同时加上x,再减去即可。
【详解】5x+1.7×3=7.4
解:5x+5.1=7.4
5x+5.1-5.1=7.4-5.1
5x=2.3
5x÷5=2.3÷5
x=0.46
-x=
解:-x+x-=-+x
x=-
x=-
x=
20.7.74平方分米
【分析】两个空白的半圆可组成一个圆,,,,据此解答。
【详解】由分析可知:
阴影面积:6×6-3.14×
=36-3.14×9
=36-28.26
=7.74(平方分米)
所以阴影部分的面积为7.74平方分米。
21.
【分析】根据减法的意义,把这节课的总时间看作单位"1”,分别减去老师讲解及同学们动手操作所用时间占的分率,即得展示做作品的时间是这节课的几分之几。
【详解】1--
=-
=-
=
答:展示作品的时间大约是这节课的。
【点睛】此题考查的是减法的意义,需明确单位“1“减去其它部分所占时间的分率即是所求的分率,还需熟练掌握异分母的减法运算是解题的关键。
22.110棵
【分析】设去年植树x棵;今年植树的棵数比去年的4倍少60棵,去年植树棵数×4-60棵=今年植树棵数,列方程:4x-60=380,解方程,即可解答。
【详解】解:设去年植树x棵。
4x-60=380
4x-60+60=380+60
4x=440
4x÷4=440÷4
x=110
答:去年植树110棵。
【点睛】本题考查方程的实际应用,利用今年植树棵数与去年植树棵数之间的关系,设出未知数,找出相关的量,列方程,解方程。
23.52.2496平方米
【分析】求小路的面积,就是求圆环的面积,根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),大圆的半径=小圆半径+小路的宽,代入数据,即可解答。
【详解】3.14×[(10+0.8)2-102]
=3.14×[10.82-100]
=3.14×[116.64-100]
=3.14×16.64
=52.2496(平方米)
答:小路的面积是52.2496平方米。
【点睛】熟练掌握圆环的面积公式是解答本题的关键。
24.15分米;7段
【分析】要把两根绳子剪成长度一样的短绳且没有剩余,求每根短绳最长是多少分米,就是求45、60的最大公因数,求两个数的最大公因数也就是这两个数的公有质因数的连乘积,可以先分别把这两个数分解质因数,再把这两个数的公有质因数相乘,最后用两条绳子的总长度数除以每段长度求出剪成的段数,由此解决问题即可。
【详解】45=3×3×5
60=2×2×3×5
所以45和60的最大公因数是:3×5=15
(45+60)÷15
=105÷15
=7(段)
答:每根绳子最长是15分米,一共能剪成这样长的短彩带7段。
【点睛】此题主要考查应用求最大公因数的知识解决实际问题,注意求两个数的最大公因数也就是这两个数的公有质因数的连乘积。
25.282.6千克
【分析】分析题意可知,根据圆的周长公式:C=2πr求出半圆形菜地的半径,再利用圆形的面积公式:S=πr2计算出菜地(半圆)的面积,最后再用菜地的面积乘20即可得解。
【详解】半圆形菜地的半径:9.42÷3.14=3(米)
半圆形菜地的面积:3.14×3×3÷2
=9.42×3÷2
=28.26÷2
=14.13(平方米)
14.13×20=282.6(千克)
答:这块菜地共可以收白菜282.6千克.
【点睛】解答此题的关键是确定半圆形菜地的半径,注意是一面靠墙。
26.(1)兔子;乌龟
(2)5;25
(3)13.3米
【分析】(1)龟兔赛跑的故事中,乌龟从始至终坚持爬行,直至胜利;兔子开始时跑步很快,中间一直在睡觉,没有前进,最后发现乌龟到达终点后又开始跑。据此,观察图中实线和虚线路程、时间的变化可知,实线表示兔子,虚线表示乌龟。
(2)表示兔子的实线从5分钟开始路程不变,30分钟之后路程增加,说明兔子出发5分钟后开始睡觉,睡了30-5=25(分钟)。
(3)从统计图中可以看出,乌龟爬行30分钟,共爬行400千米,根据路程÷时间=速度,用400除以30即可求出乌龟平均每分钟爬行多少米。
【详解】(1)实线表示兔子,虚线表示乌龟。
(2)30-5=25(分钟)
兔子出发5分钟后开始睡觉,睡了25分钟。
(3)(米)
答:乌龟平均每分钟大约爬行13.3米。
【点睛】读懂折线统计图,能根据图中的信息进行分析、计算,是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末复习卷-2024-2025学年数学五年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面计数器表示的数中,( )是3的倍数。
A. B. C. D.
2.下面四句话中,描述圆半径长度的是( )。
A.画圆时圆规两脚间的距离是2厘米 B.圆形纸片对折一次后折痕长5厘米
C.摩天轮转动一周约转过62.8米 D.喷水器旋转一周喷灌78.5平方米
3.甲、乙、丙、丁四个数在直线上的位置如下图所示,( )可能是。
A.甲 B.乙 C.丙 D.丁
4.下列式子中,( )是方程。
A.5 B.2+7=17 C.-6>4 D.16÷8=2
5.公园管理处要在一棵大榕树周围安装围树环形座椅(见示意图)。他们用一根绳子绕树干10圈,量得结果是18.84米。应选购下面( )种座椅。
A.内圆直径50厘米,外圆直径130厘米 B.内圆直径60厘米,外圆直径1.4米
C.内圆直径1米,外圆直径1.8米 D.内圆直径6米,外圆直径6.8米
6.下面四个选项中,最适合用复式折线统计图的是( )。
A.某病人一天体温变化情况 B.2023年仪征市各小学人数
C.刘辰家去年各项支出情况 D.新华书店两种图书上半年销售变化情况
7.电脑爱好者于飞设计了一个计算程序:“输入一个数→乘3→加6→输出结果”,他输入一个数后,输出结果是36,则于飞输入的数是( )。
A.10 B.12 C.14 D.114
8.某同学从家出发,按一定的速度步行去学校,途中天气有变,将要下雨,他便跑步去学校。下面各图中,能正确地表示出他行进的路程与时间关系的是( )。
A. B.
C. D.
二、填空题
9.小军用下图表示A、B两个数的公倍数,那么A、B两个数分别是( )和( ),它们的最小公倍数是( )。
10.如果2.8+x=4.3,那么x-0.42的值是( ),x÷15=( )。
11.一个最简分数,分子扩大为原来的2倍、分母缩小为原来的后等于3,这个分数原来是( )。
12.一个挂钟的时针长20厘米,这根时针走了12小时,它的尖端走了( )厘米。
13.若3个连续的奇数中,中间的一个数是a,则最小的数是( ),这三个数的和是( )。如果这三个数的和是45,那么最大的数是( )。
14.阳光体育用品商店有一个三层的球架,每层摆放的球总价相等,相同的球单价相同。从图中可以看出:
(1)一个的价格=( )个的价格。
(2)一个的价格=( )个的价格。
15.如图,把两个完全相同的三角形叠在一起,阴影部分的面积是( )平方厘米。
16.把一个圆剪拼成一个近似的长方形(如图),这个圆的面积是( )平方厘米,这个长方形的周长比圆多( )厘米。
三、计算题
17.直接写出得数。
+= -= = +=
0.48÷1.2= 0.63÷30= 3.5-2.05= 202=
18.计算下面各题,能简算的要简算。
+++
-(+) -+-
19.解方程。
5x+1.7×3=7.4 -x=
20.计算下图中阴影部分的面积。(单位:分米)
四、解答题
21.一节劳技课的时间是小时,老师讲解大约用了这节课的,同学们动手操作大约用了这节课的,其余时间用来展示作品。展示作品的时间大约是这节课的几分之几?
22.星星小区,今年植树380棵,今年植树的棵数比去年的4倍少60棵。去年植树多少棵?(列方程解答)
23.如图,一个圆形花坛的半径是10米,花坛周围有一条0.8米宽的小路。小路的面积是多少平方米?
24.把分别长45分米和60分米的两根绳子剪成长度一样的短绳且没有剩余,每根短绳最长多少分米?一共可以剪成多少段?
25.刘大伯在他家院子里靠墙围了一块半圆形的菜地,用去篱笆9.42米,若每平方米菜地可产白菜20kg,这块菜地共可以收白菜多少千克?
26.统计分析。
同学们都知道龟兔赛跑的故事吧?下面是表示龟兔赛跑比赛情况的折线统计图,请你认真读图,回答问题。
(1)实线、虚线分别表示哪种动物?实线表示( ),虚线表示( )。
(2)兔子出发( )分钟后开始睡觉,睡了( )分钟。
(3)乌龟平均每分钟爬行多少米?(得数保留一位小数)
《期末复习卷-2024-2025学年数学五年级下册苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A C B C D A C
1.D
【分析】3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数;据此解答。
【详解】A.计数器表示121,1+2+1=4,4不是3的倍数,则121不是3的倍数;
B.计数器表示304,3+0+4=7,7不是3的倍数,则304不是3的倍数;
C.计数器表示35,3+5=8,8不是3的倍数,则35不是3的倍数;
D.计数器表示243,2+4+3=9,9是3的倍数,则243是3的倍数;
故答案为:D
【点睛】本题主要考查3的倍数特征,熟练应用3的倍数特征是解题的关键。
2.A
【分析】根据对圆的半径、直径、周长、面积的认识逐项分析即可。
【详解】A.画圆时圆规两脚间的距离是2厘米,而圆规两脚间的距离就是原的半径,该选项描述的是圆半径的长度;
B.圆形纸片对折一次后折痕是圆的直径,所以圆形纸片对折一次后折痕长5厘米描述圆直径的长度;
C.摩天轮转动一周是圆的周长,所以摩天轮转动一周约转过62.8米描述圆周长;
D.喷水器旋转一周扫过的面积是圆的面积;所以喷水器旋转一周喷灌78.5平方米描述圆的面积。
故答案为:A
【点睛】本题考查对圆的半径、直径、周长、面积的认识。
3.C
【分析】化为带分数是,1<<2,且距离2比较近;据此解答。
【详解】=
在1和2之间,靠近2。结合图示可知:丙可能是。
故答案为:C
【点睛】本题主要考查假分数化带分数的方法。
4.B
【分析】含有未知数的等式叫做方程;据此解答。
【详解】A.5,含有未知数,但不是等式,所以不是方程;
B.2+7=17,既含有未知数,又是等式,所以是方程;
C.-6>4,含有未知数,但不是等式,所以不是方程;
D.16÷8=2,是等式,但不含未知数,所以不是方程。
故答案为:B
【点睛】本题考查方程的意义及应用,明确方程必须满足两个条件:一是含有未知数,二是等式。
5.C
【分析】绳子长度÷10=大榕树周长,根据圆的直径=周长÷圆周率,求出榕树直径,安装的环形座椅的内圆应该比树的周长大一点,给大榕树成长的空间,据此选择。
【详解】18.84÷10=1.884(米)
1.884÷3.14=0.6(米)=60(厘米)
A.直径小于大榕树直径,安装不上,排除;
B.直径刚好等于大榕树直径,没有留出一定距离,排除;
C.直径大于大榕树直径一些,可以;
D.直径大于大榕树直径太多,不合适,排除。
应选购内圆直径1米,外圆直径1.8米种座椅。
故答案为:C
【点睛】关键是掌握并灵活运用圆的周长公式。
6.D
【分析】条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
【详解】A.某病人一天体温变化情况,最适合用单式折线统计图;
B.2023年仪征市各小学人数,最适合用单式条形统计图;
C.刘辰家去年各项支出情况,最适合用单式条形统计图;
D.新华书店两种图书上半年销售变化情况,最适合用复式折线统计图。
最适合用复式折线统计图的是新华书店两种图书上半年销售变化情况。
故答案为:D
【点睛】关键是熟悉条形统计图和折线统计图的特点,根据统计图的特点确定最合适的统计图。
7.A
【分析】设于飞输入的数是x,根据于飞所设计的程序可列出方程3x+6=36,再根据等式的性质解方程即可求出于飞所输入的数。
【详解】解:设于飞输入的数是x。
3x+6=36
3x+6-6=36-6
3x=30
3x÷3=30÷3
x=10
所以于飞输入的数是10。
故答案为:A
【点睛】列方程解决问题时,把所求的未知数用x表示,未知数参与列式,把算术法的逆向思维转变成列方程的顺向思维来思考。
8.C
【分析】根据某学生的行驶情况,先步行(慢速行驶),再跑步(快速行驶),而图象表示行进的路程与时间的关系,可知先平缓后变陡,由此即可作出判断。
【详解】A.,观察图意可知,速度保持不变,不符合题意;
B.,先陡后相对平缓,即;先快后慢,不符合题意;
C.,先相对平缓后变陡,即先慢后快,描述了某同学行驶的过程,符合题意。
D.,先匀速行驶,再停止不变,不符合题意。
故答案为:C
【点睛】本题主要考查动点问题的图象,关键在于读懂图象所表示的意思。
9. 4 6 12
【分析】一个数最小的倍数是它本身,据此找到A、B两个数;A、B两个数的最小公倍数是它们的公倍数中最小的那一个,据此解答即可。
【详解】观察集合圈可知,A、B两个数分别是4和6,它们的最小公倍数是12。
【点睛】本题考查公倍数与最小公倍数,解答本题的关键是掌握公倍数与最小公倍数的概念。
10. 1.08 0.1
【分析】先根据等式的性质解方程2.8+x=4.3,等式左右两边同时减2.8,求出未知数x的值,然后代入求值。据此解答即可。
【详解】2.8+x=4.3
解:2.8+x-2.8=4.3-2.8
x=1.5
把x=1.5代入x-0.42中,得
x-0.42=1.5-0.42=1.08
把x=1.5代入x÷15中,得
x÷15=1.5÷15=0.1
所以,x-0.42的值是1.08,x÷15=0.1
【点睛】此题考查了根据等式的性质解方程,以及代入求值。
11.
【分析】根据题意,将这个结果倒推求解,从结果出发,逐步向前一步一步推理。在向前推理的过程中,每一步运算都是原来运算的逆运算。即:把3化成假分数,再分母乘5,分子除以2,再根据分数的基本性质,化成分子和分母只有公因数1的最简分数,即可推出原来的分数。
【详解】根据分析可得:
一个最简分数,分子扩大为原来的2倍、分母缩小为原来的后等于3,这个分数原来是。
12.125.6
【分析】时针走了12小时,就是时针走出挂钟的一圈;求尖端走的长度,就是求半径是20厘米圆的周长,根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】3.14×20×2
=62.8×2
=125.6(厘米)
一个挂钟的时针长20厘米,这根时针走了12小时,它的尖端走了125.6厘米。
13. a-2 3a 17
【分析】相邻的奇数相差2,中间数-2=最小的奇数;用中间数+2=最大的奇数,再把它们相加,即可求出这三个数的和;再用45÷3,求出中间数,再加上2,即可求出最大的数。
【详解】最小的数是(a-2);
最大的数是(a+2)
a-2+a+a+2=3a
45÷3+2
=15+2
=17
若3个连续的奇数中,中间的一个数是a,则最小的数是a-2,这三个数的和是3a。如果这三个数的和是45,那么最大的数是17。
14.(1)2
(2)3
【分析】
(1)从图中可知,第一层球架上有6个,第二层球架上有2个和2个;因为每层摆放的球总价相等,那么6个的价格=2个的价格+2个的价格,运用等式的性质得出的价格和的价格的关系。
(2)从图中可知,第三层球架上有1个、1个和1个,根据上一题的答案,用2个替换掉1个,根据第三层球架上球的价格=第一层球架上球的价格,据此得出等式,再运用等式的性质得出一个的价格相当于几个的价格。
等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
【详解】(1)
6个的价格=2个的价格+2个的价格
等式两边同时减去2个的价格,得:4个的价格=2个的价格;
等式两边同时除以2,得:2个的价格=1个的价格;
所以,一个的价格=2个的价格。
(2)
1个的价格+1个的价格+1个的价格=6个的价格
把“一个的价格=2个的价格”代入式子中,得:
1个的价格+1个的价格+2个的价格=6个的价格
即1个的价格+3个的价格=6个的价格
等式两边同时减去3个的价格,得:1个的价格=3个的价格;
所以,一个的价格=3个的价钱。
15.30
【分析】从图中分析可知,是将三角形向右平移了4厘米,即阴影部分的面积可以转化为左边梯形的面积。再根据梯形的面积=(上底+下底)×高÷2,得出阴影部分的面积。
【详解】9-3=6(厘米)
(6+9)×4÷2
=15×4÷2
=15×2
=30(平方厘米)
则阴影部分的面积是30平方厘米。
16. 50.24 8
【分析】把一个圆剪拼成一个近似的长方形,则长方形的长相当于圆周长的一半,宽相当于圆的半径;已知长方形的长为12.56厘米,则这个圆周长的一半是12.56厘米,代入圆的周长公式:C=2πr,求出圆的半径,再将半径代入圆的面积公式:S=πr2计算即可求出面积;拼成的长方形的周长比圆的周长多两条半径,用求出的半径乘2即可求出这个长方形的周长比圆多多少厘米;据此解答。
【详解】半径:12.56×2÷3.14÷2
=25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
4×2=8(厘米)
把一个圆剪拼成一个近似的长方形(如图),这个圆的面积是50.24平方厘米,这个长方形的周长比圆多8厘米。
17.;;;6;
0.4;0.021;1.45;400
【详解】略
18.;2;;1
【分析】+-,按照运算顺序,先计算加法,再计算减法;
+++,根据加法交换律,原式化为:+++,再根据加法结合律,原式化为:(+)+(+),再进行计算;
-(+),根据减法性质,原式化为:--,再根据加法交换律,原式化为:--,再进行计算;
-+-,根据加法交换律,原式化为:+--,再根据加法结合律和减法性质,原式化为:(+)-(+),再进行计算。
【详解】+-
=+-
=-
=-
=
+++
=+++
=(+)+(+)
=1+1
=2
-(+)
=--
=--
=1-
=
-+-
=+--
=(+)-(+)
=2-1
=1
19.x=0.46;x=
【分析】5x+1.7×3=7.4,先计算出1.7×3的积,再根据等式的性质1,方程两边同时减去1.7×3的积,再根据等式的性质2,方程两边同时除以5即可;
-x=,根据等式的性质1,方程两边同时加上x,再减去即可。
【详解】5x+1.7×3=7.4
解:5x+5.1=7.4
5x+5.1-5.1=7.4-5.1
5x=2.3
5x÷5=2.3÷5
x=0.46
-x=
解:-x+x-=-+x
x=-
x=-
x=
20.7.74平方分米
【分析】两个空白的半圆可组成一个圆,,,,据此解答。
【详解】由分析可知:
阴影面积:6×6-3.14×
=36-3.14×9
=36-28.26
=7.74(平方分米)
所以阴影部分的面积为7.74平方分米。
21.
【分析】根据减法的意义,把这节课的总时间看作单位"1”,分别减去老师讲解及同学们动手操作所用时间占的分率,即得展示做作品的时间是这节课的几分之几。
【详解】1--
=-
=-
=
答:展示作品的时间大约是这节课的。
【点睛】此题考查的是减法的意义,需明确单位“1“减去其它部分所占时间的分率即是所求的分率,还需熟练掌握异分母的减法运算是解题的关键。
22.110棵
【分析】设去年植树x棵;今年植树的棵数比去年的4倍少60棵,去年植树棵数×4-60棵=今年植树棵数,列方程:4x-60=380,解方程,即可解答。
【详解】解:设去年植树x棵。
4x-60=380
4x-60+60=380+60
4x=440
4x÷4=440÷4
x=110
答:去年植树110棵。
【点睛】本题考查方程的实际应用,利用今年植树棵数与去年植树棵数之间的关系,设出未知数,找出相关的量,列方程,解方程。
23.52.2496平方米
【分析】求小路的面积,就是求圆环的面积,根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),大圆的半径=小圆半径+小路的宽,代入数据,即可解答。
【详解】3.14×[(10+0.8)2-102]
=3.14×[10.82-100]
=3.14×[116.64-100]
=3.14×16.64
=52.2496(平方米)
答:小路的面积是52.2496平方米。
【点睛】熟练掌握圆环的面积公式是解答本题的关键。
24.15分米;7段
【分析】要把两根绳子剪成长度一样的短绳且没有剩余,求每根短绳最长是多少分米,就是求45、60的最大公因数,求两个数的最大公因数也就是这两个数的公有质因数的连乘积,可以先分别把这两个数分解质因数,再把这两个数的公有质因数相乘,最后用两条绳子的总长度数除以每段长度求出剪成的段数,由此解决问题即可。
【详解】45=3×3×5
60=2×2×3×5
所以45和60的最大公因数是:3×5=15
(45+60)÷15
=105÷15
=7(段)
答:每根绳子最长是15分米,一共能剪成这样长的短彩带7段。
【点睛】此题主要考查应用求最大公因数的知识解决实际问题,注意求两个数的最大公因数也就是这两个数的公有质因数的连乘积。
25.282.6千克
【分析】分析题意可知,根据圆的周长公式:C=2πr求出半圆形菜地的半径,再利用圆形的面积公式:S=πr2计算出菜地(半圆)的面积,最后再用菜地的面积乘20即可得解。
【详解】半圆形菜地的半径:9.42÷3.14=3(米)
半圆形菜地的面积:3.14×3×3÷2
=9.42×3÷2
=28.26÷2
=14.13(平方米)
14.13×20=282.6(千克)
答:这块菜地共可以收白菜282.6千克.
【点睛】解答此题的关键是确定半圆形菜地的半径,注意是一面靠墙。
26.(1)兔子;乌龟
(2)5;25
(3)13.3米
【分析】(1)龟兔赛跑的故事中,乌龟从始至终坚持爬行,直至胜利;兔子开始时跑步很快,中间一直在睡觉,没有前进,最后发现乌龟到达终点后又开始跑。据此,观察图中实线和虚线路程、时间的变化可知,实线表示兔子,虚线表示乌龟。
(2)表示兔子的实线从5分钟开始路程不变,30分钟之后路程增加,说明兔子出发5分钟后开始睡觉,睡了30-5=25(分钟)。
(3)从统计图中可以看出,乌龟爬行30分钟,共爬行400千米,根据路程÷时间=速度,用400除以30即可求出乌龟平均每分钟爬行多少米。
【详解】(1)实线表示兔子,虚线表示乌龟。
(2)30-5=25(分钟)
兔子出发5分钟后开始睡觉,睡了25分钟。
(3)(米)
答:乌龟平均每分钟大约爬行13.3米。
【点睛】读懂折线统计图,能根据图中的信息进行分析、计算,是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
