湘教版数学八年级下册 第4章 一次函数 单元测试(含答案)
文档属性
| 名称 | 湘教版数学八年级下册 第4章 一次函数 单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 123.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览



文档简介
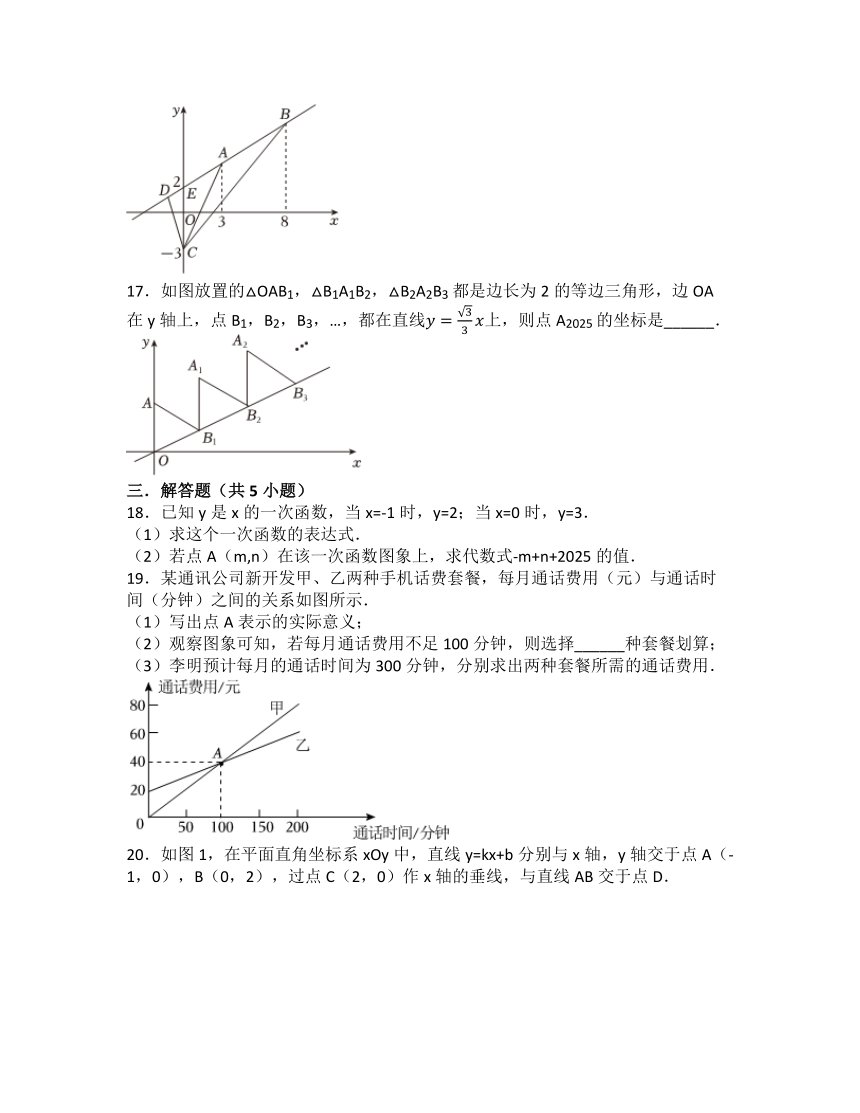
湘教版八年级下 第4章 一次函数 单元测试
一.选择题(共12小题)
1.(2025春 上海校级期中)下列关于变量x、y的关系式中,y是关于x的一次函数的是( )
A.y=1 B.y=kx+b(k、b为常数)
C.y=(a2+1)x-3(a为常数) D.
2.下列图形中不能表示y是x的函数的是( )
A. B. C. D.
3.下列函数中,是y关于x的一次函数的是( )
A.y=3x-5 B.y=x2 C. D.
4.点A(2,y1)和B(1,y2)都在直线y=x-2上,则y1与y2的关系是( )
A.y1≥y2 B.y1≤y2 C.y1<y2 D.y1>y2
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=2x-k的图象可能是( )
A. B. C. D.
6.电信公司手机的收费标准有A,B两类,已知每月应缴费用S(元)与通话时间t(分)之间的关系如图所示.当通话时间为200分钟时,按这两类收费标准缴费的差为( )
A.10元 B.15元 C.20元 D.30元
7.已知一次函数y=(3m-1)x+m-4图象经过原点,则下列结论正确的是( )
A.m=-4 B.m=2 C.m=±4 D.m=4
8.如图,已知点K为直线l:y=2x+4上一点,先将点K向左平移a个单位,再向下平移b个单位至点K1,若点K1恰好落在直线l上,则a,b应满足的关系是( )
A.2a-b=0 B.2a+b=0 C.2a-b=4 D.2a+b=4
9.在平面直角坐标系中,将正比例函数y=-2x的图象向右平移3个单位长度,得到一个一次函数的图象,则这个一次函数的表达式为( )
A.y=-2x+3 B.y=-2x-3 C.y=-2x-6 D.y=-2x+6
10.如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向上平移得l2,l2与x轴、y轴分别交于点A、点B,若OB=6,则线段OA的长为( )
A.3 B.4 C. D.
11.如图,从光源A发出一束光,经x轴上的一点B(-4,0)反射后,得到光线BC,光线BC经y轴上一点C反射后,得到光线CD.若AB∥CD,且光线AB所在直线的函数表达式为,则光线CD所在直线的函数表达式为( )
A. B. C.y=-2x+2 D.
12.已知甲,乙两地相距480km,一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距120km,货车改变速度
继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离y(km)与货车行驶时间x(h)之间的函数图象,则下列说法错误的是( )
A.a=120
B.点F的坐标为(8,0)
C.出租车从乙地返回甲地的速度为128km/h
D.出租车返回的过程中,货车出发或都与出租车相距12km
二.填空题(共5小题)
13.将一次函数的图象沿y轴向下平移4个单位长度,则平移之后图象的函数表达式为 ______.
14.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.-1.5)两点,那么当y<0时,自变量x的取值范围是 ______.
15.若点A(2,y1),点B(-1,y2),点C(3,1)都在一次函数y=-kx+10的图象上,则y1与y2的大小关系是 ______.
16.如图,在平面直角坐标系中,△ABC的顶点A,B的横坐标分别为3和8,顶点C的坐标为(0,-3),直线AB与y轴交于点E(0,2),点D为直线AB上任意一点,连接CD,若AB=6,则CD的最小值为 ______.
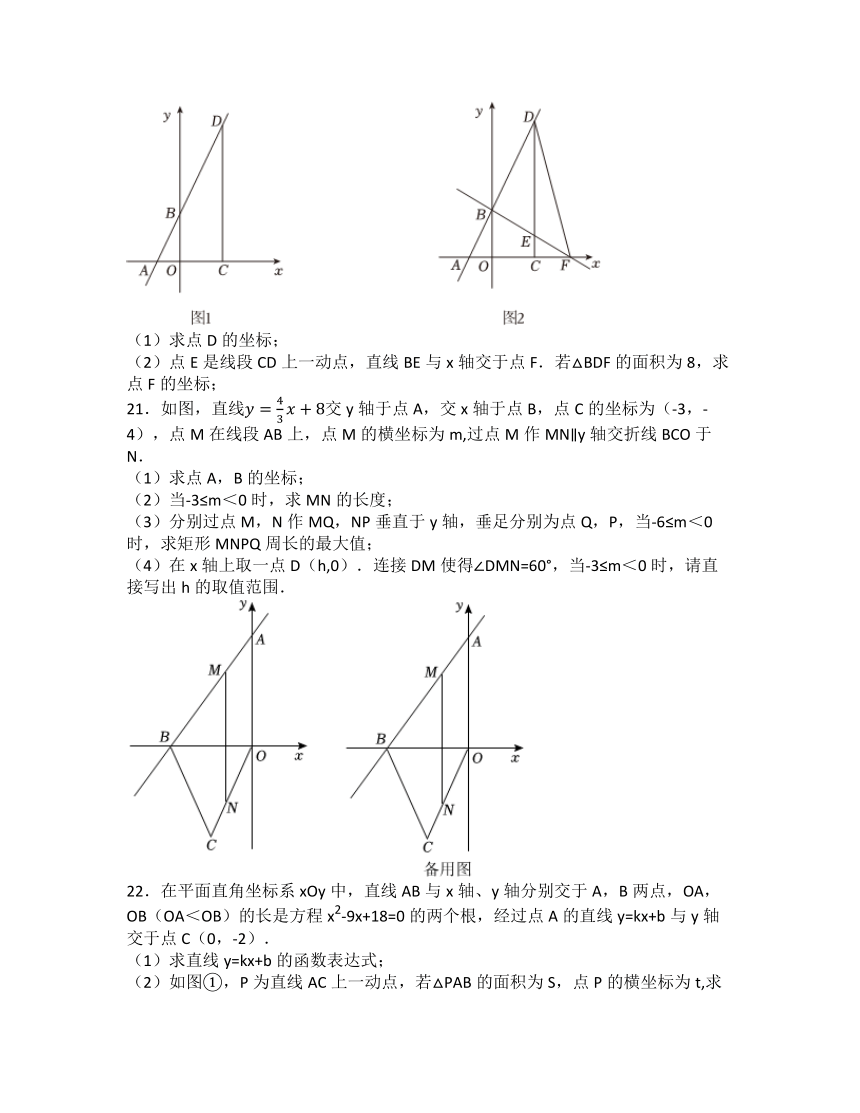
17.如图放置的△OAB1,△B1A1B2,△B2A2B3都是边长为2的等边三角形,边OA在y轴上,点B1,B2,B3,…,都在直线上,则点A2025的坐标是______.
三.解答题(共5小题)
18.已知y是x的一次函数,当x=-1时,y=2;当x=0时,y=3.
(1)求这个一次函数的表达式.
(2)若点A(m,n)在该一次函数图象上,求代数式-m+n+2025的值.
19.某通讯公司新开发甲、乙两种手机话费套餐,每月通话费用(元)与通话时间(分钟)之间的关系如图所示.
(1)写出点A表示的实际意义;
(2)观察图象可知,若每月通话费用不足100分钟,则选择______种套餐划算;
(3)李明预计每月的通话时间为300分钟,分别求出两种套餐所需的通话费用.
20.如图1,在平面直角坐标系xOy中,直线y=kx+b分别与x轴,y轴交于点A(-1,0),B(0,2),过点C(2,0)作x轴的垂线,与直线AB交于点D.
(1)求点D的坐标;
(2)点E是线段CD上一动点,直线BE与x轴交于点F.若△BDF的面积为8,求点F的坐标;
21.如图,直线交y轴于点A,交x轴于点B,点C的坐标为(-3,-4),点M在线段AB上,点M的横坐标为m,过点M作MN∥y轴交折线BCO于N.
(1)求点A,B的坐标;
(2)当-3≤m<0时,求MN的长度;
(3)分别过点M,N作MQ,NP垂直于y轴,垂足分别为点Q,P,当-6≤m<0时,求矩形MNPQ周长的最大值;
(4)在x轴上取一点D(h,0).连接DM使得∠DMN=60°,当-3≤m<0时,请直接写出h的取值范围.
22.在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于A,B两点,OA,OB(OA<OB)的长是方程x2-9x+18=0的两个根,经过点A的直线y=kx+b与y轴交于点C(0,-2).
(1)求直线y=kx+b的函数表达式;
(2)如图①,P为直线AC上一动点,若△PAB的面积为S,点P的横坐标为t,求S与t的函数关系式;
(3)如图②,将△AOB沿着x轴向右平移得到△A'O'B',在平面直角坐标系内是否存在点M,使得以A',B',B,M为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
湘教版八年级下 第4章 一次函数 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、D 3、A 4、D 5、C 6、C 7、D 8、A 9、D 10、A 11、D 12、D
二.填空题(共5小题)
13、; 14、x<2; 15、y1<y2; 16、; 17、;
三.解答题(共5小题)
18、解:(1)设一次函数解析式为y=kx+b,
根据题意得,
解得,
∴一次函数解析式为y=x+3;
(2)把A(m,n)代入y=x+3得n=m+3,
所以-m+n+2025=-m+m+3+2025=2028.
19、解:(1)根据题意,
点A表示的实际意义是:通话时间为100分钟,甲、乙两种套餐的通话费用都是40元.
(2)根据图象可知,
当时间t<100时,甲种话费套餐在乙种手机话费的下方,若每月通话费用不足100分钟,则选择甲种套餐划算.
故答案为:甲;
(3)根据题意,
甲种套餐的费用:300×=120元,
乙种套餐的费用:300×+20=80元.
20、解:(1)∵点A(-1,0),B(0,2),
∴直线AB的解析式为y=2x+2,
∵CD⊥x轴,
∴点D的横坐标为2,
∴y=6,
∴点D的坐标为:(2,6);
(2)设F(m,0)有两种情况;
①当F在C点右侧时,
∵D(2,6),A(-1,0),B(0,2),DC⊥x轴.
∴S△ADF=AF DC=(m+1)×6=3(m+1),S△ABF=AF OB=(m+1)×2=m+l.
∵S△BDF=8,
∴S△ADF=S△ABF+S△DBF,即:3(m+1)=m+1+8
∴m=3.
∴F(3,0);
②当F点在C点左侧时,
∵点A(-1,0),B(0,2),C(2,0),D(2,6).
∴S△ADF=AF×CD=(-1-m)×6=-3-3m,S△ABF=AF×OB=(-1-m)×2-=-1-m,
∴S△BDF=S△ADF-S△ABF=8,
∴-(-3-3m)-(-1-m)=8,解得:m=-5,
∴F(-5,0);
综上所述:F(-5,0)或(3,0).
21、解:(1)对于,当x=0时,y=8,令y=0,则x=-6,
即点A、B的坐标分别为:(0,8)、(-6,0);
(2)由点B、C的坐标得,直线BC的表达式为:y=-x-8,同理可得,直线OC的表达式为:y=x,
设点M(m,m+8),点N(m,m),
则MN=m+8-m=8;
(3)设点M(m,m+8),点N(m,m)或(m,-m-8),
则MN=m+8-(-m-8)=m+16或MN=8,而MQ=-m,
当-6≤m≤-3时,
矩形MNPQ周长=2(MN+MQ)=2(m+16-m)=m+32,
当m=-6时,矩形MNPQ周长的最大值为22;
当-3<m<0时,
矩形MNPQ周长=2(MN+MQ)=2(8-m)=16-2m,
当m=0时,周长为16,
故矩形MNPQ周长的最大值为22;
(4)由(1)知MN=8,点M、N关于x轴对撑,则MT=4,
则Rt△DMT中,MT=4,∠DMN=60°,则DT=4,
即|h-m|=4,而-3≤m<0,
故-3-4≤h<-4或-3+4≤h<4.
22、解:(1)∵x2-9x+18=0,则x=3或6,
即点A、B的坐标分别为:(-3,0)、(0,6),
设直线的表达式为:y=kx-2,
将点A的坐标代入上式得:0=-3k-2,则k=-,
则函数的表达式为:y=-x-2;
(2)设点P(t,-t-2),
当点P在点A左侧时,
∵点B(0,6),点C(0,-2),
∴BC=8,
∵S△PAB=(-t)×8-=-4t-12;
当点P在点A右侧时,
同理可得:
S△PAB=×t×8+×8×3=4t+12,
综上所述:S=|4t+12|;
(3)存在,理由:
如图,连接BB',A'B,
∵点A(-3,0),点B(0,6),
∴AO=3,BO=6,则AB=3,
∵将△AOB沿着x轴向右平移得到△A'O'B',
∴AB=A'B'=3,BB'∥AA',BB'=AA',当BB',A'B'为边时,
∵A'B'BM是菱形,
∴BB'=A'B'=3=A'M,BB'∥A'M,
即点A与点M重合,
∴M(-3,0);
当A'B'与A'B为边时,
∵四边形A'BMB'是菱形,
∴A'B=A'B'=AB,
∴AO=A'O=3,
∴点A'(3,0),
∵A'M与BB'互相垂直平分,
∴点M(3,12);
当BB'与A'B为边时,
∵四边形A'BB'M是菱形,
∴BM垂直平分A'B',
∴BM⊥AB,
又∵BO⊥AM,
∴△ABO∽△BMO,
∴BO:AO=OM:OB,
则OM==12,
∴点M(12,0),
综上所述:点M的坐标为(-3,0)或(3,12)或(12,0).
一.选择题(共12小题)
1.(2025春 上海校级期中)下列关于变量x、y的关系式中,y是关于x的一次函数的是( )
A.y=1 B.y=kx+b(k、b为常数)
C.y=(a2+1)x-3(a为常数) D.
2.下列图形中不能表示y是x的函数的是( )
A. B. C. D.
3.下列函数中,是y关于x的一次函数的是( )
A.y=3x-5 B.y=x2 C. D.
4.点A(2,y1)和B(1,y2)都在直线y=x-2上,则y1与y2的关系是( )
A.y1≥y2 B.y1≤y2 C.y1<y2 D.y1>y2
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=2x-k的图象可能是( )
A. B. C. D.
6.电信公司手机的收费标准有A,B两类,已知每月应缴费用S(元)与通话时间t(分)之间的关系如图所示.当通话时间为200分钟时,按这两类收费标准缴费的差为( )
A.10元 B.15元 C.20元 D.30元
7.已知一次函数y=(3m-1)x+m-4图象经过原点,则下列结论正确的是( )
A.m=-4 B.m=2 C.m=±4 D.m=4
8.如图,已知点K为直线l:y=2x+4上一点,先将点K向左平移a个单位,再向下平移b个单位至点K1,若点K1恰好落在直线l上,则a,b应满足的关系是( )
A.2a-b=0 B.2a+b=0 C.2a-b=4 D.2a+b=4
9.在平面直角坐标系中,将正比例函数y=-2x的图象向右平移3个单位长度,得到一个一次函数的图象,则这个一次函数的表达式为( )
A.y=-2x+3 B.y=-2x-3 C.y=-2x-6 D.y=-2x+6
10.如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向上平移得l2,l2与x轴、y轴分别交于点A、点B,若OB=6,则线段OA的长为( )
A.3 B.4 C. D.
11.如图,从光源A发出一束光,经x轴上的一点B(-4,0)反射后,得到光线BC,光线BC经y轴上一点C反射后,得到光线CD.若AB∥CD,且光线AB所在直线的函数表达式为,则光线CD所在直线的函数表达式为( )
A. B. C.y=-2x+2 D.
12.已知甲,乙两地相距480km,一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距120km,货车改变速度
继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离y(km)与货车行驶时间x(h)之间的函数图象,则下列说法错误的是( )
A.a=120
B.点F的坐标为(8,0)
C.出租车从乙地返回甲地的速度为128km/h
D.出租车返回的过程中,货车出发或都与出租车相距12km
二.填空题(共5小题)
13.将一次函数的图象沿y轴向下平移4个单位长度,则平移之后图象的函数表达式为 ______.
14.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.-1.5)两点,那么当y<0时,自变量x的取值范围是 ______.
15.若点A(2,y1),点B(-1,y2),点C(3,1)都在一次函数y=-kx+10的图象上,则y1与y2的大小关系是 ______.
16.如图,在平面直角坐标系中,△ABC的顶点A,B的横坐标分别为3和8,顶点C的坐标为(0,-3),直线AB与y轴交于点E(0,2),点D为直线AB上任意一点,连接CD,若AB=6,则CD的最小值为 ______.
17.如图放置的△OAB1,△B1A1B2,△B2A2B3都是边长为2的等边三角形,边OA在y轴上,点B1,B2,B3,…,都在直线上,则点A2025的坐标是______.
三.解答题(共5小题)
18.已知y是x的一次函数,当x=-1时,y=2;当x=0时,y=3.
(1)求这个一次函数的表达式.
(2)若点A(m,n)在该一次函数图象上,求代数式-m+n+2025的值.
19.某通讯公司新开发甲、乙两种手机话费套餐,每月通话费用(元)与通话时间(分钟)之间的关系如图所示.
(1)写出点A表示的实际意义;
(2)观察图象可知,若每月通话费用不足100分钟,则选择______种套餐划算;
(3)李明预计每月的通话时间为300分钟,分别求出两种套餐所需的通话费用.
20.如图1,在平面直角坐标系xOy中,直线y=kx+b分别与x轴,y轴交于点A(-1,0),B(0,2),过点C(2,0)作x轴的垂线,与直线AB交于点D.
(1)求点D的坐标;
(2)点E是线段CD上一动点,直线BE与x轴交于点F.若△BDF的面积为8,求点F的坐标;
21.如图,直线交y轴于点A,交x轴于点B,点C的坐标为(-3,-4),点M在线段AB上,点M的横坐标为m,过点M作MN∥y轴交折线BCO于N.
(1)求点A,B的坐标;
(2)当-3≤m<0时,求MN的长度;
(3)分别过点M,N作MQ,NP垂直于y轴,垂足分别为点Q,P,当-6≤m<0时,求矩形MNPQ周长的最大值;
(4)在x轴上取一点D(h,0).连接DM使得∠DMN=60°,当-3≤m<0时,请直接写出h的取值范围.
22.在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于A,B两点,OA,OB(OA<OB)的长是方程x2-9x+18=0的两个根,经过点A的直线y=kx+b与y轴交于点C(0,-2).
(1)求直线y=kx+b的函数表达式;
(2)如图①,P为直线AC上一动点,若△PAB的面积为S,点P的横坐标为t,求S与t的函数关系式;
(3)如图②,将△AOB沿着x轴向右平移得到△A'O'B',在平面直角坐标系内是否存在点M,使得以A',B',B,M为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
湘教版八年级下 第4章 一次函数 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、D 3、A 4、D 5、C 6、C 7、D 8、A 9、D 10、A 11、D 12、D
二.填空题(共5小题)
13、; 14、x<2; 15、y1<y2; 16、; 17、;
三.解答题(共5小题)
18、解:(1)设一次函数解析式为y=kx+b,
根据题意得,
解得,
∴一次函数解析式为y=x+3;
(2)把A(m,n)代入y=x+3得n=m+3,
所以-m+n+2025=-m+m+3+2025=2028.
19、解:(1)根据题意,
点A表示的实际意义是:通话时间为100分钟,甲、乙两种套餐的通话费用都是40元.
(2)根据图象可知,
当时间t<100时,甲种话费套餐在乙种手机话费的下方,若每月通话费用不足100分钟,则选择甲种套餐划算.
故答案为:甲;
(3)根据题意,
甲种套餐的费用:300×=120元,
乙种套餐的费用:300×+20=80元.
20、解:(1)∵点A(-1,0),B(0,2),
∴直线AB的解析式为y=2x+2,
∵CD⊥x轴,
∴点D的横坐标为2,
∴y=6,
∴点D的坐标为:(2,6);
(2)设F(m,0)有两种情况;
①当F在C点右侧时,
∵D(2,6),A(-1,0),B(0,2),DC⊥x轴.
∴S△ADF=AF DC=(m+1)×6=3(m+1),S△ABF=AF OB=(m+1)×2=m+l.
∵S△BDF=8,
∴S△ADF=S△ABF+S△DBF,即:3(m+1)=m+1+8
∴m=3.
∴F(3,0);
②当F点在C点左侧时,
∵点A(-1,0),B(0,2),C(2,0),D(2,6).
∴S△ADF=AF×CD=(-1-m)×6=-3-3m,S△ABF=AF×OB=(-1-m)×2-=-1-m,
∴S△BDF=S△ADF-S△ABF=8,
∴-(-3-3m)-(-1-m)=8,解得:m=-5,
∴F(-5,0);
综上所述:F(-5,0)或(3,0).
21、解:(1)对于,当x=0时,y=8,令y=0,则x=-6,
即点A、B的坐标分别为:(0,8)、(-6,0);
(2)由点B、C的坐标得,直线BC的表达式为:y=-x-8,同理可得,直线OC的表达式为:y=x,
设点M(m,m+8),点N(m,m),
则MN=m+8-m=8;
(3)设点M(m,m+8),点N(m,m)或(m,-m-8),
则MN=m+8-(-m-8)=m+16或MN=8,而MQ=-m,
当-6≤m≤-3时,
矩形MNPQ周长=2(MN+MQ)=2(m+16-m)=m+32,
当m=-6时,矩形MNPQ周长的最大值为22;
当-3<m<0时,
矩形MNPQ周长=2(MN+MQ)=2(8-m)=16-2m,
当m=0时,周长为16,
故矩形MNPQ周长的最大值为22;
(4)由(1)知MN=8,点M、N关于x轴对撑,则MT=4,
则Rt△DMT中,MT=4,∠DMN=60°,则DT=4,
即|h-m|=4,而-3≤m<0,
故-3-4≤h<-4或-3+4≤h<4.
22、解:(1)∵x2-9x+18=0,则x=3或6,
即点A、B的坐标分别为:(-3,0)、(0,6),
设直线的表达式为:y=kx-2,
将点A的坐标代入上式得:0=-3k-2,则k=-,
则函数的表达式为:y=-x-2;
(2)设点P(t,-t-2),
当点P在点A左侧时,
∵点B(0,6),点C(0,-2),
∴BC=8,
∵S△PAB=(-t)×8-=-4t-12;
当点P在点A右侧时,
同理可得:
S△PAB=×t×8+×8×3=4t+12,
综上所述:S=|4t+12|;
(3)存在,理由:
如图,连接BB',A'B,
∵点A(-3,0),点B(0,6),
∴AO=3,BO=6,则AB=3,
∵将△AOB沿着x轴向右平移得到△A'O'B',
∴AB=A'B'=3,BB'∥AA',BB'=AA',当BB',A'B'为边时,
∵A'B'BM是菱形,
∴BB'=A'B'=3=A'M,BB'∥A'M,
即点A与点M重合,
∴M(-3,0);
当A'B'与A'B为边时,
∵四边形A'BMB'是菱形,
∴A'B=A'B'=AB,
∴AO=A'O=3,
∴点A'(3,0),
∵A'M与BB'互相垂直平分,
∴点M(3,12);
当BB'与A'B为边时,
∵四边形A'BB'M是菱形,
∴BM垂直平分A'B',
∴BM⊥AB,
又∵BO⊥AM,
∴△ABO∽△BMO,
∴BO:AO=OM:OB,
则OM==12,
∴点M(12,0),
综上所述:点M的坐标为(-3,0)或(3,12)或(12,0).
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
