3.2整式的加减(第1课时) 教学课件(共21张PPT)初中数学北师大版(2024)七年级上册
文档属性
| 名称 | 3.2整式的加减(第1课时) 教学课件(共21张PPT)初中数学北师大版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 21.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 19:28:50 | ||
图片预览








文档简介
(共21张PPT)
3.2整式的加减
(第1课时)
第三章 整式及其加减
北师大版(2024)七年级上册
学习目标
准确理解并掌握同类项的概念与特点
01
理解合并同类项的法则和步骤,能熟练正确地合并同类项
02
知识引入
生活中处处存在分类,请对下类水果进行分类.
知识探究
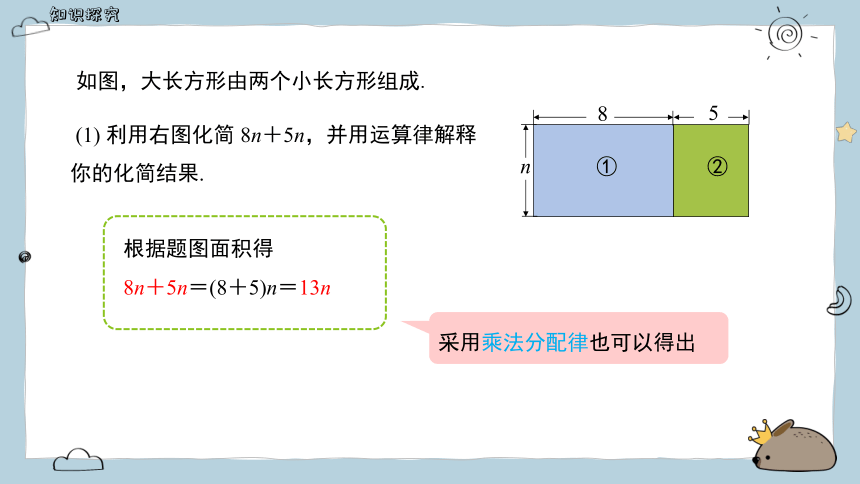
如图,大长方形由两个小长方形组成.
8
5
n
①
②
根据题图面积得
8n+5n=(8+5)n=13n
采用乘法分配律也可以得出
(1) 利用右图化简 8n+5n,并用运算律解释你的化简结果.
知识探究
如图,大长方形由两个小长方形组成.
8
5
n
①
②
根据乘法对加法的分配律可得
2xy+3xy=(2+3)xy=5xy
-7a2b+2a2b=(-7+2)a2b=-5a2b
(2) 你能用类似的方法化简 2xy+3xy 及
-7a2b+2a2b 吗?
字母可以和数一样进行计算.
知识探究
像 8n 与 5n ,2xy 与 3xy ,-7a2 b 与 2a2b 这样所含字母相同,并且相同字母的指数也相同的项,叫作同类项.
把同类项合并成一项叫作合并同类项.
例如:8n+5n=13n,2xy+3xy=5xy,
-7a2b+2a2b=-5a2b.
(1)都是单项式;
(2)与系数无关;
(3)与字母的顺序无关;
(4)几个常数项也是同类项.
典型例题
例1 根据乘法对加法的分配律合并同类项:
(1) -xy2+3xy2; (2) 7a+3a2+2a-a2+3.
解:(1)-xy2+3xy2
=(-1+3)xy2
=2xy2.
(2) 7a+3a2+2a-a2+3
=(7a+2a)+(3a2-a2)+3
=(7+2)a+(3-1) a2+3
=9a+2a2+3.
合并同类项时,把同类项的系数相加,字母和字母的指数不变.
典型例题
例2 合并同类项:
(1) 3a+2b-5a-b
=(3a-5a)+(2b-b)
=-2a+b
=(3-5)a+(2-1)b
解:(1) 3a+2b-5a-b
(2)-4ab+b2-9ab- b2
(2) -4ab+b2-9ab- b2
=(-4ab-9ab)+(b2-b2)
=-13ab-b2
=(-4-9)ab+()b2
知识探究
合并同类项的一般步骤:
(1)找出多项式中的同类项;
(2)通过交换律把同类项放在一起,交换位置时一定不要丢掉单项式前面的符号;
(3)把同类项的系数相加,字母和字母的指数不变.
知识探究
尝试·交流
解:-3x2y+5x-0.5x2y+3.5x2y-2
=(-3x2y-0.5x2y+3.5x2y)+5x-2
=(-3-0.5+3.5)x2y+5x-2
=5x-2
一般情况下,先化简再代入求解.
-3x2y+5x-0.5x2y+3.5x2y-2
求代数式-3x2y+5x-0.5x2y+3.5x2y-2的值,其中 x= ,y=7 .
当 x= ,y=7 时,原式=5× -2=-1
当堂检测
D
A
C
C
D
同类项的概念:
化简并求值:一般情况下,先化简再求值.
整式的加减
合并同类项:
所含字母相同,且相同字母的指数也相同的项叫做同类项.
(1)找出多项式中的同类项;
(2)通过交换律把同类项放在一起,交换位置时一定不要丢掉单项式前面的符号;
(3)把同类项的系数相加,字母和字母的指数不变.
感谢观看
3.2整式的加减
(第1课时)
第三章 整式及其加减
北师大版(2024)七年级上册
学习目标
准确理解并掌握同类项的概念与特点
01
理解合并同类项的法则和步骤,能熟练正确地合并同类项
02
知识引入
生活中处处存在分类,请对下类水果进行分类.
知识探究
如图,大长方形由两个小长方形组成.
8
5
n
①
②
根据题图面积得
8n+5n=(8+5)n=13n
采用乘法分配律也可以得出
(1) 利用右图化简 8n+5n,并用运算律解释你的化简结果.
知识探究
如图,大长方形由两个小长方形组成.
8
5
n
①
②
根据乘法对加法的分配律可得
2xy+3xy=(2+3)xy=5xy
-7a2b+2a2b=(-7+2)a2b=-5a2b
(2) 你能用类似的方法化简 2xy+3xy 及
-7a2b+2a2b 吗?
字母可以和数一样进行计算.
知识探究
像 8n 与 5n ,2xy 与 3xy ,-7a2 b 与 2a2b 这样所含字母相同,并且相同字母的指数也相同的项,叫作同类项.
把同类项合并成一项叫作合并同类项.
例如:8n+5n=13n,2xy+3xy=5xy,
-7a2b+2a2b=-5a2b.
(1)都是单项式;
(2)与系数无关;
(3)与字母的顺序无关;
(4)几个常数项也是同类项.
典型例题
例1 根据乘法对加法的分配律合并同类项:
(1) -xy2+3xy2; (2) 7a+3a2+2a-a2+3.
解:(1)-xy2+3xy2
=(-1+3)xy2
=2xy2.
(2) 7a+3a2+2a-a2+3
=(7a+2a)+(3a2-a2)+3
=(7+2)a+(3-1) a2+3
=9a+2a2+3.
合并同类项时,把同类项的系数相加,字母和字母的指数不变.
典型例题
例2 合并同类项:
(1) 3a+2b-5a-b
=(3a-5a)+(2b-b)
=-2a+b
=(3-5)a+(2-1)b
解:(1) 3a+2b-5a-b
(2)-4ab+b2-9ab- b2
(2) -4ab+b2-9ab- b2
=(-4ab-9ab)+(b2-b2)
=-13ab-b2
=(-4-9)ab+()b2
知识探究
合并同类项的一般步骤:
(1)找出多项式中的同类项;
(2)通过交换律把同类项放在一起,交换位置时一定不要丢掉单项式前面的符号;
(3)把同类项的系数相加,字母和字母的指数不变.
知识探究
尝试·交流
解:-3x2y+5x-0.5x2y+3.5x2y-2
=(-3x2y-0.5x2y+3.5x2y)+5x-2
=(-3-0.5+3.5)x2y+5x-2
=5x-2
一般情况下,先化简再代入求解.
-3x2y+5x-0.5x2y+3.5x2y-2
求代数式-3x2y+5x-0.5x2y+3.5x2y-2的值,其中 x= ,y=7 .
当 x= ,y=7 时,原式=5× -2=-1
当堂检测
D
A
C
C
D
同类项的概念:
化简并求值:一般情况下,先化简再求值.
整式的加减
合并同类项:
所含字母相同,且相同字母的指数也相同的项叫做同类项.
(1)找出多项式中的同类项;
(2)通过交换律把同类项放在一起,交换位置时一定不要丢掉单项式前面的符号;
(3)把同类项的系数相加,字母和字母的指数不变.
感谢观看
同课章节目录
