浙江省宁波市鄞州区2024学年第二学期八年级期末模拟练习(含答案)
文档属性
| 名称 | 浙江省宁波市鄞州区2024学年第二学期八年级期末模拟练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 347.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 15:40:47 | ||
图片预览



文档简介
浙江省宁波市鄞州区2024学年第二学期八年级期末模拟练习
一、选择题(每小题3分,共30分)
1.二次根式在实数范围内有意义,则x应满足的条件是( )
A. B. C. D.
2.我国有56个民族,各民族的传统服饰图案各具特色.下列图案既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.下列各式计算正确的是( )
A. B. C. D.
4.如图,四边形是平行四边形,若,则的度数是( )
A. B. C. D.
5.一元二次方程x2-2x-1=0配方后可变形为( )
A.(x-1)2=0 B.(x+1)2=0 C.(x-1)2=2 D.(x+1)2=2
6.用反证法证明命题“已知,求证:.”的第一步应先假设( )
A. B. C. D.
7.在长为,宽为的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为,求道路的宽度设道路的宽度为,则可列方程( ).
A. B.
C. D.
8.某篮球队 5 名场上队员的身高 (单位: ) 分别是: . 现用一名身高为 的队员换下场上身高为 的队员,与换人前相比,换人后场上队员的身高
A.平均数变小, 方差变小 B.平均数变小, 方差变大
C.平均数变大, 方差变小 D.平均数变大, 方差变大
9.已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上,当x1<x2<x3时,则下列判断正确的是( )
A.若x1+x2<0,则y2 y3>0 B.若y1 y3<0,则x2 x3>0
C.若x2+x3<0,则y1 y2>0 D.若y2 y3<0,则x1 x3>0
10.如图,AC是正方形ABCD的对角线,点E是CD上一点,连结BE,分别过点A和C作BE的垂线,垂足分别为G和F,BE与AC交于点H,O是AC的中点,连结OF,OG,AB=5,有下列结论:①当AG=4时,FG=1;②OG平分∠AGE.关于这两个结论,下列说法正确的是( )
A.①②都对 B.①对,②错 C.①错,②对 D.①②都错
二、填空题(每小题3分,共18分)
11.一个多边形的内角和是,这个多边形的边数为 .
12.若是关于x的方程的解,则的值为 .
13.最简二次根式能与合并,则 .
14.如图,在正方形中,,分别为边、的中点,连接、,点分别为、的中点,连接,则的长是 .
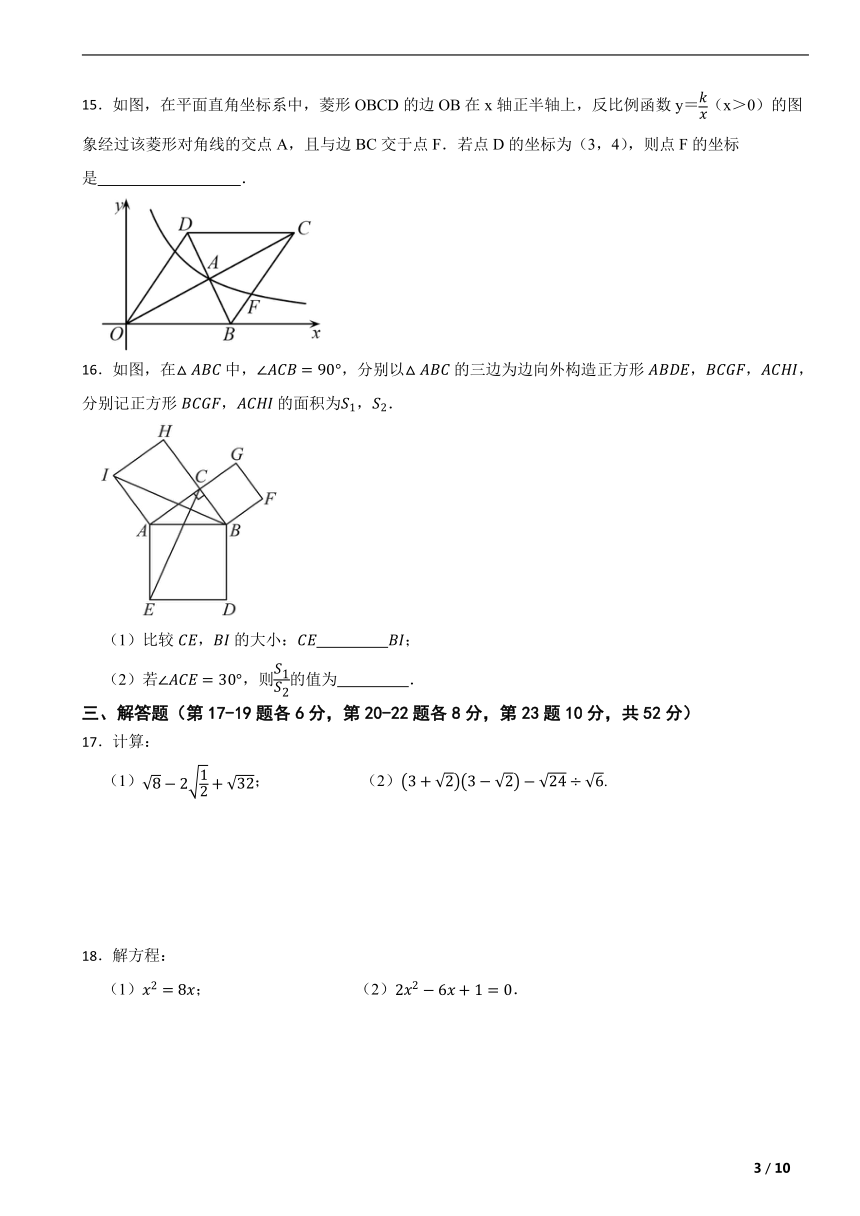
15.如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是 .
16.如图,在中,,分别以的三边为边向外构造正方形,,,分别记正方形,的面积为,.
(1)比较,的大小: ;
(2)若,则的值为 .
三、解答题(第17-19题各6分,第20-22题各8分,第23题10分,共52分)
17.计算:
(1); (2).
18.解方程:
(1); (2).
19.学校为加强学生垃圾分类方面的知识普及,开设了垃圾分类臻善德育小课培训学习,为了解培训效果,学校对七年级544名学生在学习前和培训后各进行一次垃圾分类知晓情况检测,两次检测项目相同,政教处依据同一标准进行问卷评估,分成“合格”、“良好”、“优秀”3个等级,依次记为2分、6分、8分,学校随机抽取32名学生的2次检测等级作为样本,绘制成如图的条形统计图:
(1)这32名学生在培训前得分的中位数对应等级应为 ;(填“合格”、“良好”或“优秀”)
(2)求这32名学生培训后比培训前的平均分提高了多少?
(3)利用样本估计该校七年级学生中,培训后检测等级为“良好”与“优秀”的学生人数之和是多少
20.某商店销售一款电风扇,平均每天可售出24台,每台利润60元.为了增加利润,商店准备适当降价,若每台电风扇每降价5元,平均每天将多售出4台.设每台电风扇降价元.
(1)降价后平均每天的销售量为 ,每台的利润为 .
(2)若要使每天销售利润达到1540元,求的值.
(3)请问该电风扇每天销售利润能否达到2000元吗?请说明理由.
21.如图,菱形中,对角线交于点,点是的中点,延长到点,使,连接.
(1)求证:四边形是矩形;
(2)若,,求菱形的面积.
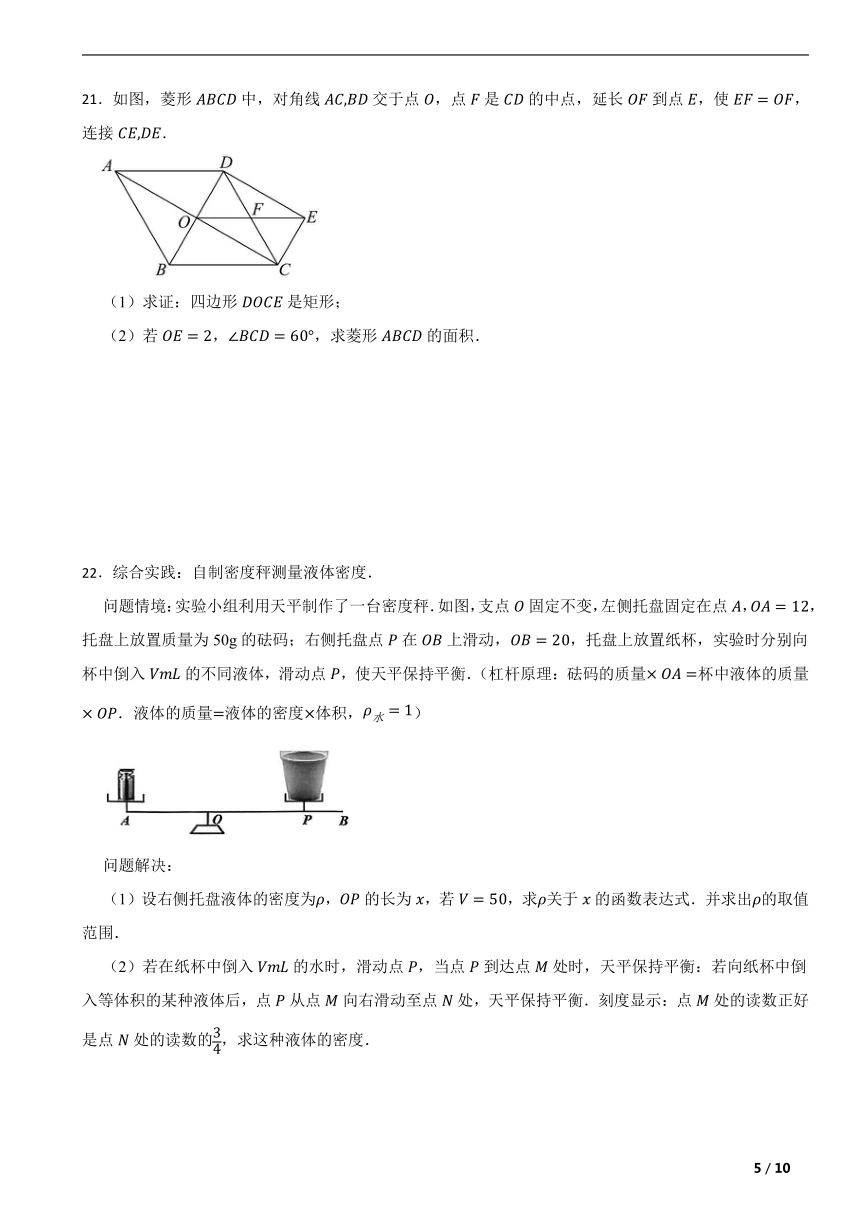
22.综合实践:自制密度秤测量液体密度.
问题情境:实验小组利用天平制作了一台密度秤.如图,支点固定不变,左侧托盘固定在点,,托盘上放置质量为50g的砝码;右侧托盘点在上滑动,,托盘上放置纸杯,实验时分别向杯中倒入的不同液体,滑动点,使天平保持平衡.(杠杆原理:砝码的质量杯中液体的质量.液体的质量液体的密度体积,)
问题解决:
(1)设右侧托盘液体的密度为,的长为,若,求关于的函数表达式.并求出的取值范围.
(2)若在纸杯中倒入的水时,滑动点,当点到达点处时,天平保持平衡:若向纸杯中倒入等体积的某种液体后,点从点向右滑动至点处,天平保持平衡.刻度显示:点处的读数正好是点处的读数的,求这种液体的密度.
23. 在矩形中,,,点E,F分别在边,上,将沿直线折叠,点C的对应点为点G.
(1)如图1,当点F与点B重合,点G落在上时,求的长;
(2)如图2,当点E是的中点,且时,连接,求的长;
(3)如图3,当,点G恰好落在上时,延长交于点H,直接写出的长.
参考答案
1.A
2.B
3.C
4.A
5.C
6.A
7.A
8.A
9.C
10.A
11.9
12.
13.
14.
15.(6,).
16.;
17.(1)解:
(2)解:
18.(1)解:
(2)解:
,
19.(1)合格
(2)解:培训前的平均分为:(25×2+5×6+2×8)÷32=3(分)
培训后的平均分为:(8×2+16×6+8×8)÷32=5.5(分)
培训后比培训前的平均分提高2.5分
(3)解:样本中培训后“良好”的比例为:
样本中培训后“优秀”的比例为:
培训后考分等级为“良好”与“优秀”的学生共有(名).
20.(1)24+4x;60-5x
(2)解:依题意,可列方程:
(60-5x)(24+4x)=1540,
解方程得:,
答:x的值为1或5
(3)解:不能。依题意,可列方程:(60-5x)(24+4x)=2000,
化简得x2-6x+28=0,
Δ=(-6)2-4×1×28=-76<0.
故方程无实数根.
故该电风扇每天销售利润不能达到2000元
21.(1)证明:∵点是的中点,∴,
∵,
∴四边形是平行四边形,
∵四边形是菱形,
∴,即,
∴四边形是矩形
(2)解:∵四边形是矩形,,∴,
∵四边形是菱形,
∴,,,,
∵,
∴,
∴,,
∴,,
∴四边形的面积为.
22.(1)解:根据杠杆平衡原理可得:,
即,
∴,
∵,
∴;
(2)解:设点处的读数为,则点N处的读数为,
即,,
根据杠杆平衡条件得:,
,
∴,
即,
∵,
∴.
23.(1)解:∵四边形是矩形,
,,
由折叠的性质,得,
在中,由勾股定理,得.
(2)解:四边形是矩形,,,,
点是的中点,
,
由折叠的性质,得,.
,
,
四边形是矩形.
又∵,
四边形是正方形.
,
,
在中,由勾股定理,得.
(3)解:如图,连接,,
四边形是矩形,
,,.
,
在中,由勾股定理,得,
由折叠的性质,得,,
,,
.
在和中,
,
,
,
设,则,
在中,由勾股定理,得,
在中,由勾股定理,得,
,解得:,
的长为.
1 / 1
一、选择题(每小题3分,共30分)
1.二次根式在实数范围内有意义,则x应满足的条件是( )
A. B. C. D.
2.我国有56个民族,各民族的传统服饰图案各具特色.下列图案既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.下列各式计算正确的是( )
A. B. C. D.
4.如图,四边形是平行四边形,若,则的度数是( )
A. B. C. D.
5.一元二次方程x2-2x-1=0配方后可变形为( )
A.(x-1)2=0 B.(x+1)2=0 C.(x-1)2=2 D.(x+1)2=2
6.用反证法证明命题“已知,求证:.”的第一步应先假设( )
A. B. C. D.
7.在长为,宽为的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为,求道路的宽度设道路的宽度为,则可列方程( ).
A. B.
C. D.
8.某篮球队 5 名场上队员的身高 (单位: ) 分别是: . 现用一名身高为 的队员换下场上身高为 的队员,与换人前相比,换人后场上队员的身高
A.平均数变小, 方差变小 B.平均数变小, 方差变大
C.平均数变大, 方差变小 D.平均数变大, 方差变大
9.已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上,当x1<x2<x3时,则下列判断正确的是( )
A.若x1+x2<0,则y2 y3>0 B.若y1 y3<0,则x2 x3>0
C.若x2+x3<0,则y1 y2>0 D.若y2 y3<0,则x1 x3>0
10.如图,AC是正方形ABCD的对角线,点E是CD上一点,连结BE,分别过点A和C作BE的垂线,垂足分别为G和F,BE与AC交于点H,O是AC的中点,连结OF,OG,AB=5,有下列结论:①当AG=4时,FG=1;②OG平分∠AGE.关于这两个结论,下列说法正确的是( )
A.①②都对 B.①对,②错 C.①错,②对 D.①②都错
二、填空题(每小题3分,共18分)
11.一个多边形的内角和是,这个多边形的边数为 .
12.若是关于x的方程的解,则的值为 .
13.最简二次根式能与合并,则 .
14.如图,在正方形中,,分别为边、的中点,连接、,点分别为、的中点,连接,则的长是 .
15.如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是 .
16.如图,在中,,分别以的三边为边向外构造正方形,,,分别记正方形,的面积为,.
(1)比较,的大小: ;
(2)若,则的值为 .
三、解答题(第17-19题各6分,第20-22题各8分,第23题10分,共52分)
17.计算:
(1); (2).
18.解方程:
(1); (2).
19.学校为加强学生垃圾分类方面的知识普及,开设了垃圾分类臻善德育小课培训学习,为了解培训效果,学校对七年级544名学生在学习前和培训后各进行一次垃圾分类知晓情况检测,两次检测项目相同,政教处依据同一标准进行问卷评估,分成“合格”、“良好”、“优秀”3个等级,依次记为2分、6分、8分,学校随机抽取32名学生的2次检测等级作为样本,绘制成如图的条形统计图:
(1)这32名学生在培训前得分的中位数对应等级应为 ;(填“合格”、“良好”或“优秀”)
(2)求这32名学生培训后比培训前的平均分提高了多少?
(3)利用样本估计该校七年级学生中,培训后检测等级为“良好”与“优秀”的学生人数之和是多少
20.某商店销售一款电风扇,平均每天可售出24台,每台利润60元.为了增加利润,商店准备适当降价,若每台电风扇每降价5元,平均每天将多售出4台.设每台电风扇降价元.
(1)降价后平均每天的销售量为 ,每台的利润为 .
(2)若要使每天销售利润达到1540元,求的值.
(3)请问该电风扇每天销售利润能否达到2000元吗?请说明理由.
21.如图,菱形中,对角线交于点,点是的中点,延长到点,使,连接.
(1)求证:四边形是矩形;
(2)若,,求菱形的面积.
22.综合实践:自制密度秤测量液体密度.
问题情境:实验小组利用天平制作了一台密度秤.如图,支点固定不变,左侧托盘固定在点,,托盘上放置质量为50g的砝码;右侧托盘点在上滑动,,托盘上放置纸杯,实验时分别向杯中倒入的不同液体,滑动点,使天平保持平衡.(杠杆原理:砝码的质量杯中液体的质量.液体的质量液体的密度体积,)
问题解决:
(1)设右侧托盘液体的密度为,的长为,若,求关于的函数表达式.并求出的取值范围.
(2)若在纸杯中倒入的水时,滑动点,当点到达点处时,天平保持平衡:若向纸杯中倒入等体积的某种液体后,点从点向右滑动至点处,天平保持平衡.刻度显示:点处的读数正好是点处的读数的,求这种液体的密度.
23. 在矩形中,,,点E,F分别在边,上,将沿直线折叠,点C的对应点为点G.
(1)如图1,当点F与点B重合,点G落在上时,求的长;
(2)如图2,当点E是的中点,且时,连接,求的长;
(3)如图3,当,点G恰好落在上时,延长交于点H,直接写出的长.
参考答案
1.A
2.B
3.C
4.A
5.C
6.A
7.A
8.A
9.C
10.A
11.9
12.
13.
14.
15.(6,).
16.;
17.(1)解:
(2)解:
18.(1)解:
(2)解:
,
19.(1)合格
(2)解:培训前的平均分为:(25×2+5×6+2×8)÷32=3(分)
培训后的平均分为:(8×2+16×6+8×8)÷32=5.5(分)
培训后比培训前的平均分提高2.5分
(3)解:样本中培训后“良好”的比例为:
样本中培训后“优秀”的比例为:
培训后考分等级为“良好”与“优秀”的学生共有(名).
20.(1)24+4x;60-5x
(2)解:依题意,可列方程:
(60-5x)(24+4x)=1540,
解方程得:,
答:x的值为1或5
(3)解:不能。依题意,可列方程:(60-5x)(24+4x)=2000,
化简得x2-6x+28=0,
Δ=(-6)2-4×1×28=-76<0.
故方程无实数根.
故该电风扇每天销售利润不能达到2000元
21.(1)证明:∵点是的中点,∴,
∵,
∴四边形是平行四边形,
∵四边形是菱形,
∴,即,
∴四边形是矩形
(2)解:∵四边形是矩形,,∴,
∵四边形是菱形,
∴,,,,
∵,
∴,
∴,,
∴,,
∴四边形的面积为.
22.(1)解:根据杠杆平衡原理可得:,
即,
∴,
∵,
∴;
(2)解:设点处的读数为,则点N处的读数为,
即,,
根据杠杆平衡条件得:,
,
∴,
即,
∵,
∴.
23.(1)解:∵四边形是矩形,
,,
由折叠的性质,得,
在中,由勾股定理,得.
(2)解:四边形是矩形,,,,
点是的中点,
,
由折叠的性质,得,.
,
,
四边形是矩形.
又∵,
四边形是正方形.
,
,
在中,由勾股定理,得.
(3)解:如图,连接,,
四边形是矩形,
,,.
,
在中,由勾股定理,得,
由折叠的性质,得,,
,,
.
在和中,
,
,
,
设,则,
在中,由勾股定理,得,
在中,由勾股定理,得,
,解得:,
的长为.
1 / 1
同课章节目录
