第四章三角形期末单元复习题(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
第四章三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
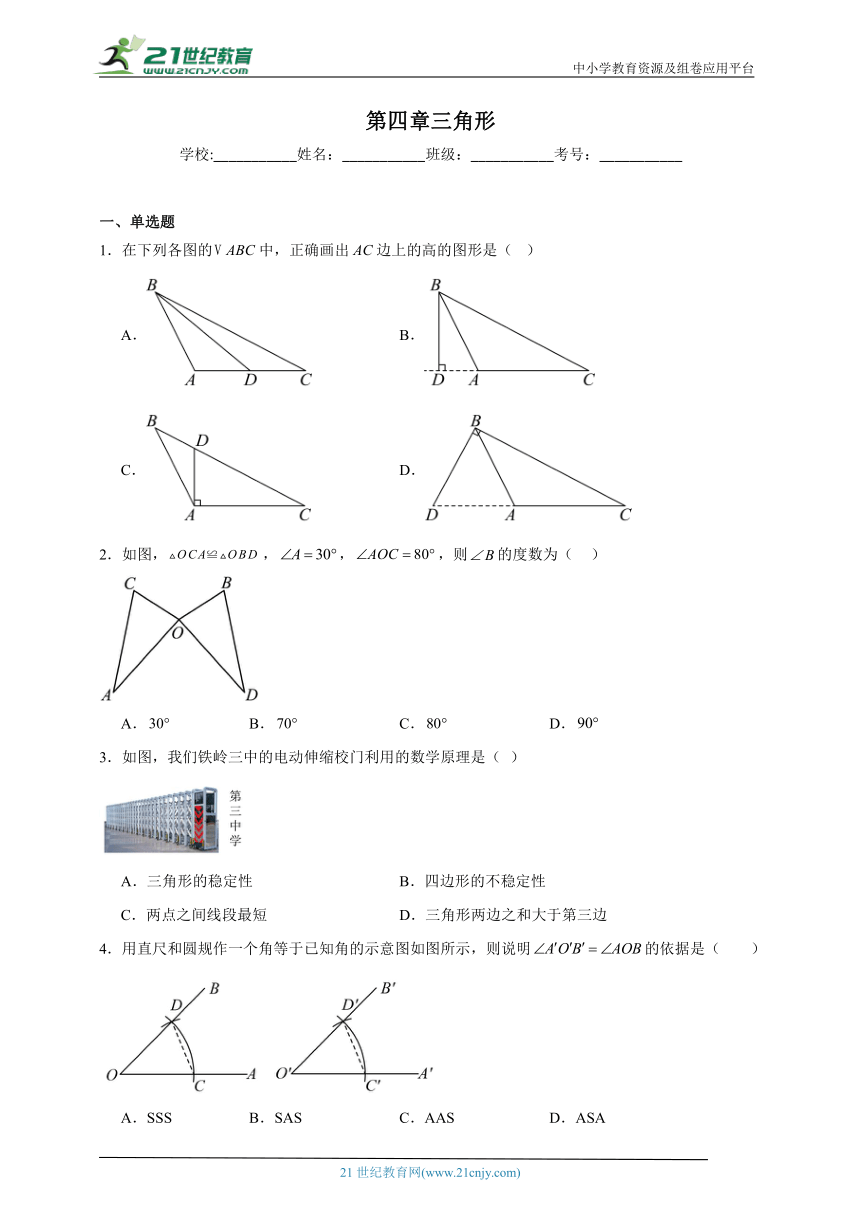
1.在下列各图的中,正确画出边上的高的图形是( )
A. B.
C. D.
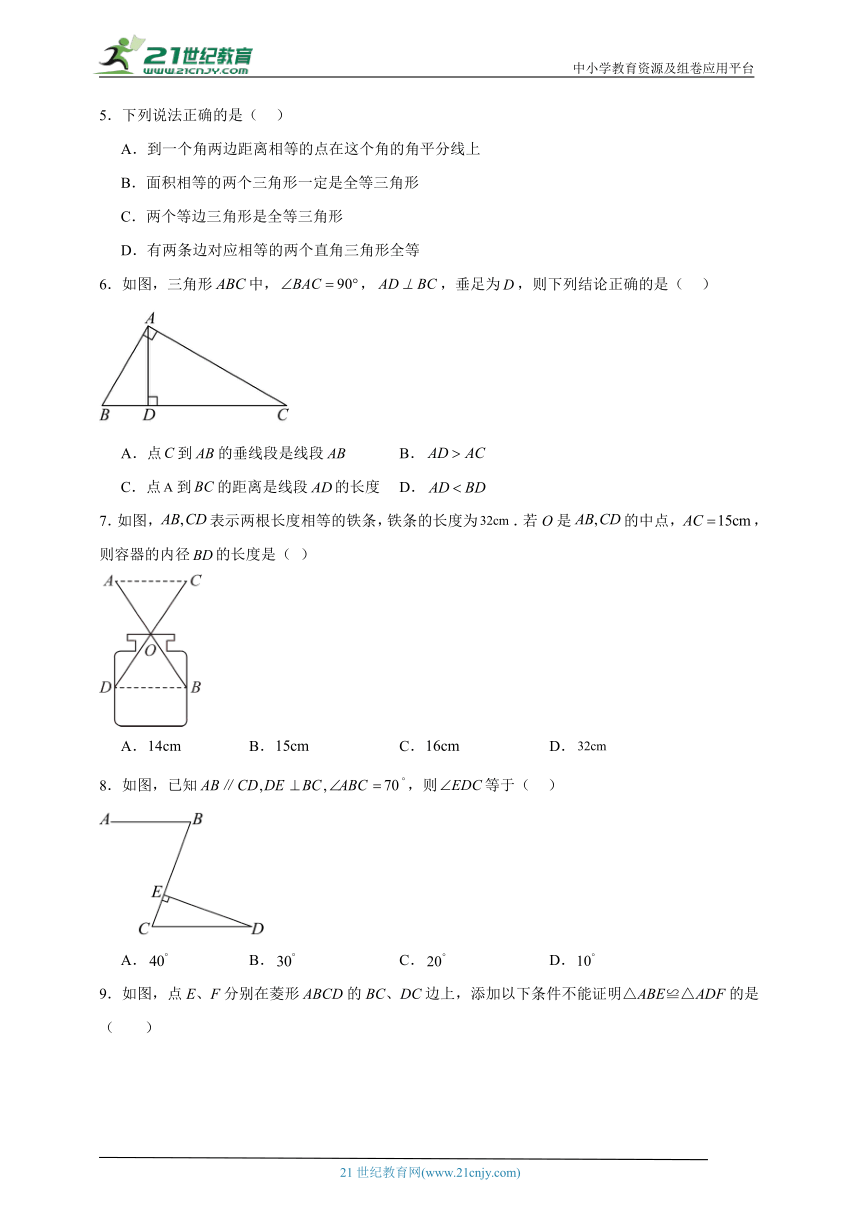
2.如图,,,,则的度数为( )
A. B. C. D.
3.如图,我们铁岭三中的电动伸缩校门利用的数学原理是( )
A.三角形的稳定性 B.四边形的不稳定性
C.两点之间线段最短 D.三角形两边之和大于第三边
4.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( )
A.SSS B.SAS C.AAS D.ASA
5.下列说法正确的是( )
A.到一个角两边距离相等的点在这个角的角平分线上
B.面积相等的两个三角形一定是全等三角形
C.两个等边三角形是全等三角形
D.有两条边对应相等的两个直角三角形全等
6.如图,三角形中,,,垂足为,则下列结论正确的是( )
A.点到的垂线段是线段 B.
C.点到的距离是线段的长度 D.
7.如图,表示两根长度相等的铁条,铁条的长度为.若O是的中点,,则容器的内径的长度是( )
A. B. C. D.
8.如图,已知,则等于( )
A. B. C. D.
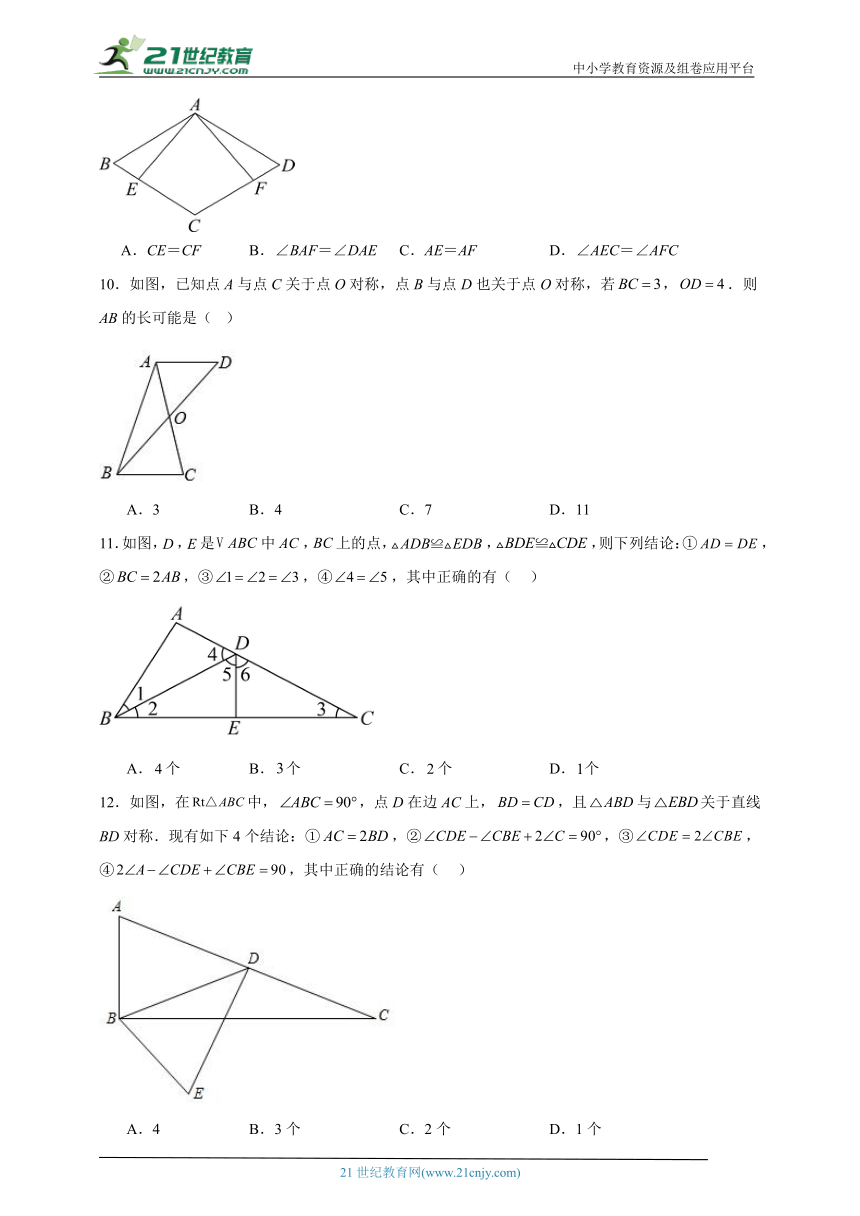
9.如图,点E、F分别在菱形ABCD的BC、DC边上,添加以下条件不能证明△ABE≌△ADF的是( )
A.CE=CF B.∠BAF=∠DAE C.AE=AF D.∠AEC=∠AFC
10.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,.则AB的长可能是( )
A.3 B.4 C.7 D.11
11.如图,,是中,上的点,,,则下列结论:①,②,③,④,其中正确的有( )
A.个 B.个 C.个 D.个
12.如图,在中,,点D在边AC上,,且与关于直线BD对称.现有如下4个结论:①,②,③,④,其中正确的结论有( )
A.4 B.3个 C.2个 D.1个
二、填空题
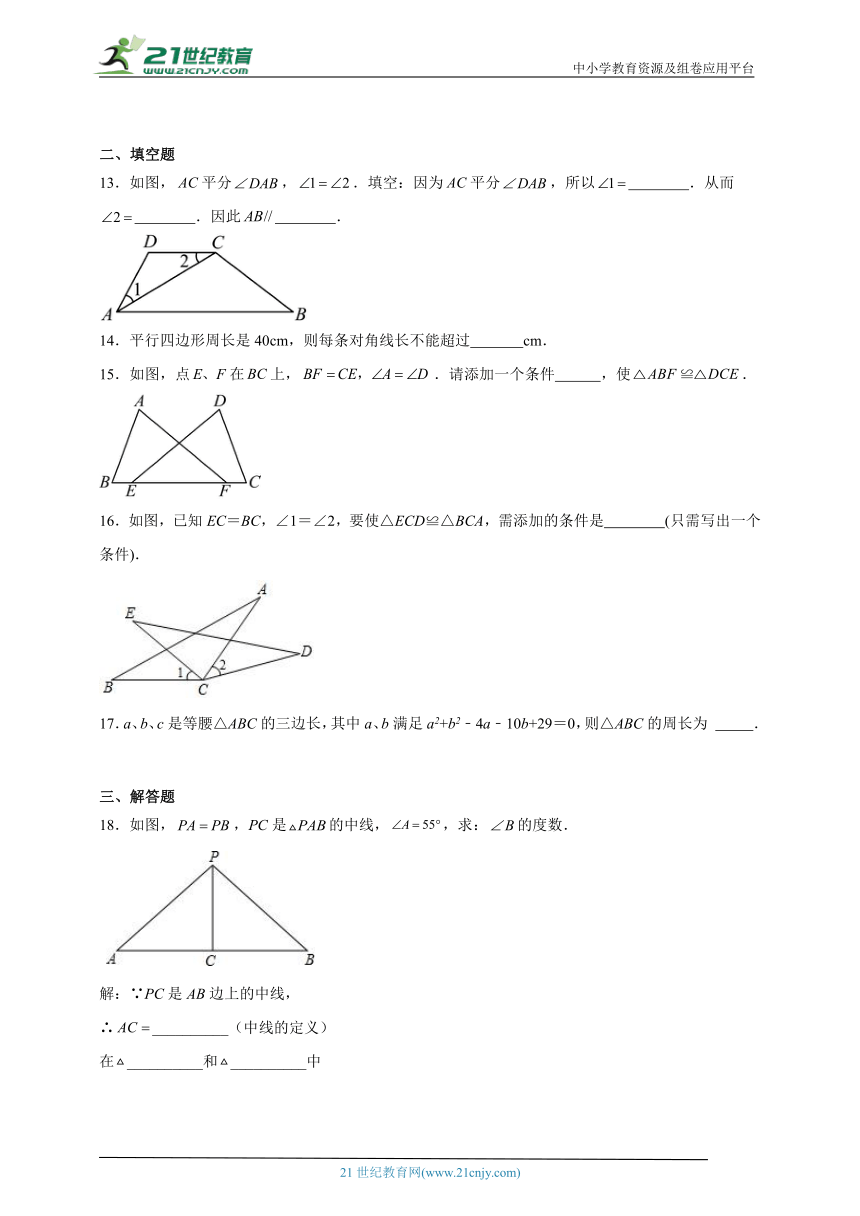
13.如图,平分,.填空:因为平分,所以 .从而 .因此 .
14.平行四边形周长是40cm,则每条对角线长不能超过 cm.
15.如图,点在上,.请添加一个条件 ,使.
16.如图,已知EC=BC,∠1=∠2,要使△ECD≌△BCA,需添加的条件是 (只需写出一个条件).
17.a、b、c是等腰△ABC的三边长,其中a、b满足a2+b2﹣4a﹣10b+29=0,则△ABC的周长为 .
三、解答题
18.如图,,PC是的中线,,求:的度数.
解:∵PC是AB边上的中线,
∴__________(中线的定义)
在__________和__________中
∴____________________(________)
∴(______________________)
∵(已知)
∴(等量代换)
19.如图,和关于直线对称,与的交点在直线上.
(1)图中点的对应点是点 ,的对应角是 ;
(2)若,,则的长为 ;
(3)若,,求的度数.
20.如下图,已知,写出该组全等三角形的对应边和剩余的对应角.
21.如图,在边长为1个单位的正方形网格中,经过平移后得到,图中标出了点B的对应点.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
(1)画出;
(2)画出的高;
(3)连接、,那么与的关系是 ,线段AC扫过的图形的面积为 .
(4)在AB的右侧确定格点Q,使的面积和的面积相等,这样的Q点有 个.
22.已知:如图,,.
(1)AB与CD有怎样的位置关系?请证明你的结论.
(2)你还能发现哪些结论?
23.某中学七(2)班学生到户外活动,为了测量池塘两端A,B之间的距离,设计了如下方案:
如图,先过点B作的垂线,再在上取C,D两点,使,接着过点D作的垂线,交的延长线于点E,则测出的长即为点A,B之间的距离.
阅读后回答下列问题:
(1)此方案是否可行?请说明理由;
(2)方案中作的目的是什么?若,方案是否仍然成立(无须说明理由)?
24.【问题探究】
(1)如图①,在中,,的平分线交于点,于点.
①试说明:;
②如图②,点是线段上一点,连接,且,判断与之间的数量关系,并说明理由;
【问题解决】
(2)若图②中的是某市的一块空地,,和是三条小路(小路宽度忽略不计),现要在区域内种植鲜花,已知区域的面积为,,,求种植鲜花的面积(即的面积).
《第四章三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A D C B C C C
题号 11 12
答案 A A
1.B
【分析】本题考查了三角形的高,关键是利用基本作图作三角形高的方法解答.根据三角形的高的概念判断即可.
【详解】解:边上的高就是过顶点B作垂线段,垂直,交的延长线于D点,因此只有B符合条件,
故选:B.
2.B
【分析】在中由三角形内角和180°可求出,由全等三角形对应角相等可得即可求解.
【详解】解∶在中,,
∴
又∵,
∴,
故选B.
【点睛】本题考查三角形内角和与全等三角形的性质,熟记相应的概念是解题的关键.
3.B
【分析】本题考查了四边形的性质,根据电动伸缩门的工作原理,结合四边形的不稳定性即可得到答案,熟练掌握四边形的相关知识的解题的关键.
【详解】解:∵电动伸缩门的整体形状为四边形,且电动伸缩门的长度可以伸长和变短,
∴利用的数学原理是四边形的不稳定性,
故选:.
4.A
【分析】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键.
根据尺规作图可知,可证,得到,即可得到结论.
【详解】解:直尺和圆规作一个角等于已知角可得,
,
,
,
故选:A .
5.D
【分析】根据角平分线的判定可判断选项A错误,根据全等三角形的判定可判断选项B、C错误,选项D正确,即可得.
【详解】解:A、根据角平分线的判定“角的内部到角的两边的距离相等的点在角平分线上”,选项说法错误,不符合题意;
B、能够完全重合的两个三角形叫做全等三角形,选项说法错误,不符合题意;
C、两个等边三角形不是全等三角形,再有一条对应边相等才行,选项说法错误,不符合题意;
D、有两条边对应相等的两个直角三角形全等,选项说法正确,符合题意;
故选D.
【点睛】本题考查了角平分线,全等三角形的判定,解题的关键是掌握这些知识点.
6.C
【分析】根据三角形的三边关系和垂线段最短即可得到结论.
【详解】解:A、点到的垂线段是线段,故选项错误,不符合题意;
B、在中,是直角边,是斜边,故,故选项错误,不符合题意;
C、点到的距离是线段的长度,故选项正确,符合题意;
D、在中,和都是直角边,故,无法判断大小,故错误,不符合题意;
故选:C.
【点睛】本题考查了三角形的三边关系,垂线段最短,解题的关键是正确的识别图形.
7.B
【分析】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.只要证明,即可推出.
【详解】解:是的中点,,
在和中,
故选:B.
8.C
【分析】本题考查了平行线的性质和直角三角形两锐角互余的性质,掌握相关的性质是解题的关键.先根据平行线性质求出,再在直角三角形中利用直角三角形两锐角互余求出.
【详解】解:,
,
,
,
,
故选:C.
9.C
【分析】由四边形是菱形可得:,,再根据每个选项添加的条件逐一判断.
【详解】解:由四边形是菱形可得:,,
A、由CE=CF ,可得,可用证明,故不符合题意;
B、添加,可用证明,故不符合题意;
C、添加,不能证明,故符合题意;
D、由∠AEC=∠AFC ,可得,可用证明,故不符合题意;
故选:C.
【点睛】本题考查菱形性质及全等三角形的判定,解题的关键是掌握三角形全等的判定定理.
10.C
【分析】根据三角形三边关系定理,可知即可求解.
【详解】解:∵点与点关于点对称,点与点也关于点对称,
∴,
又∵∠AOD=∠BOC
∴△AOD≌△BOC(SAS)
∴AD=BC=3
∵
∴.
故选:C.
【点睛】本题考查了三角形三边关系定理:任意两边之和大于第三边,及对称的性质,全等三角形的判定与性质,解题的关键是将求AB的值转化为求三角形第三边的取值范围.
11.A
【分析】本题主要考查了全等三角形的性质,解题的关键是掌握全等三角形的对应角、对应边相等.根据全等三角形的性质,对每一项分别分析、解答出即可.
【详解】解:,
,,,,
故①④正确;
,
,,
,,
,
故②③正确;
综上,正确的有①②③④,共个,
故选:A.
12.A
【分析】根据等边对等角可得∠C=∠DBC,根据直角三角形两锐角互余和等角的余角相等可判断①;
根据折叠前后对应角相等和角的和差分别表示∠CBE和∠CDE,即可判断③;
代入到②④等式的左边与右边比较可判断②和④;
【详解】解:∵∠ABC=90°,
∴∠A+∠C=90°,∠ABD+∠DBC=90°,
∵BD=CD,
∴∠C=∠DBC,
∴∠ADB=∠DBC+∠C=2∠C,∠A=∠ABD,
∴AD=BD,即AC=AD+CD=2BD,①正确;
根据折叠的性质可知∠DBE=∠ABD,∠ADB=∠BDE,
∴∠DBE=∠ABD=∠A,∠ADB=∠BDE=2∠C,
∴∠CBE=2∠A-90°,∠CDE=180°-4∠C,
∴
,②正确;
∵,
∴,③正确;
∴,④正确;
综上所述,正确的有4个,
故选:A.
【点睛】本题考查三角形外角的性质,等边对等角,折叠问题,直角三角形两锐角互余等.解决此题的关键是熟练掌握定理,分别正确表示相应角.
13.
【分析】由AC平分∠DAB,∠1=∠2,可得出∠CAB=∠2,由内错角相等可以得出两直线平行.
【详解】解:∵AC平分∠DAB,
∴∠1=∠CAB.
又∵∠1=∠2,
∴∠CAB=∠2,
∴ABDC(内错角相等,两直线平行).
故答案为:∠CAB,∠CAB,DC.
【点睛】本题考查了平行线的判定定理以及角平分线的定义,解题的关键是找出∠CAB=∠2.解决该类题型只需牢牢掌握平行线的判定定理即可.
14.20
【分析】根据平行四边形的性质和三角形三边关系进行求解即可.
【详解】解:如图所示,平行四边形ABCD中,
,
在△ABD中,由三边关系知:,
∴,
同理可得,
即:每条对角线长不能超过20cm,
故答案为:20.
【点睛】本题考查平行四边形的性质以及三角形的三边关系,理解基本性质以及熟练综合运用基本结论是解题关键.
15.(答案不唯一)
【分析】本题考查了全等三角形的判定.根据已知条件中的一边一角,再添加一组对角相等即可.
【详解】解:∵,
再添加,
根据“角角边”就能证明.
故答案为:(答案不唯一).
16.DC=AC(答案不唯一)
【分析】由∠1=∠2可得∠ECD=∠BCA,再由EC=BC,添加DC=AC,利用“SAS”判定两个三角形全等.
【详解】解:添加的条件是DC=AC,理由如下:
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ECD=∠BCA,
在△ECD和△BCA中,
,
∴△ECD≌△BCA(SAS).
故答案为DC=AC.
【点睛】本题考查了全等三角形的判定定理.熟记全等三角形的判定定理是解题的关键.
17.12
【分析】先利用完全平方公式把a2+b2﹣4a﹣10b+29=0化为再利用非负数的性质求解 再分两种情况讨论:当为腰时,当为底时,结合三角形的三边关系,从而可得答案.
【详解】解: a2+b2﹣4a﹣10b+29=0,
a、b、c是等腰△ABC的三边长,
当为腰时,则另一腰 此时 三角形不存在,舍去,
当为底时,则腰 此时 三角形存在,
△ABC的周长为
故答案为:12
【点睛】本题考查的是利用完全平方公式分解因式,非负数的性质,三角形三边的关系,等腰三角形的定义,掌握以上基础知识是解题的关键.
18.见解析.
【分析】根据三角形中线的定义和全等三角形的判定与性质分别填空即可.
【详解】解:是边上的中线,
(中线的定义).
在和中,
,
,
(全等三角形对应角相等).
(已知),
(等量代换).
故答案为:,,,PB,BC,PC,PC,公共边,,,SSS,全等三角形对应角相等.
【点睛】本题考查了全等三角形的判定与性质,三角形中线的定义,主要是对逻辑推理能力的训练,熟记全等三角形的判定方法是解题的关键.
19.(1)E,
(2)3
(3)
【分析】本题主要考查了轴对称,成轴对称的两个图形的全等性:
(1)观察图形可直接得出答案;
(2)根据成轴对称的两个图形的全等性可得,根据全等三角形对应边相等即可求解;
(3)根据,,推出,根据对称性得到,推出.
【详解】(1)解:∵和关于直线对称,
∴图中点C的对应点是点E,的对应角是;
故答案为:E,.
(2)解:∵和关于直线对称,
∴,
∴,
∵,
∴.
故答案为:3.
(3)解:∵,,
∴,
根据对称性知,,
∴.
20.该组全等三角形的对应边为与与与,剩余的对应角为与.
【分析】本题考查了全等三角形的性质,根据全等三角形的对应边相等,对应角相等,即可作答.
【详解】解:∵,
∴该组全等三角形的对应边为与与与,剩余的对应角为与.
21.(1)
(2)见解析
(3),,10
(4)8
【分析】(1)分别作出,,的对应点,,即可.
(2)根据三角形高的定义画出图形即可.
(3)利用分割法求解即可.
(4)作关于的对称点,利用等高模型解决问题即可.
【详解】(1)如图,即为所求作.
(2)如图,线段即为所求作.
(3),,
线段扫过的图形的面积为.
故答案为:,,10
(4)满足条件的点有8个,
故答案为:8.
22.(1),证明见解析
(2),
【分析】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
(1),理由为:连接,由两直线平行内错角相等得到一对角相等,再由已知角相等及公共边,利用得到三角形全等,利用全等三角形对应边相等即可得证;
(2)还能得到与平行,.
【详解】(1)解:,理由如下:
连接,
,
,
在和中,
,
,
;
(2)还能确定出:,
23.(1)可行,见解析
(2)目的见解析,成立
【分析】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键:
(1)证明,可得到,故此方案可行.
(2)根据全等三角形的性质解答即可.
【详解】(1)解:此方案可行.理由如下:
由题意可知,,
所以.
在和中,
所以,
所以.
故此方案可行.
(2)作的目的是为了使,同时简化测量过程,提高测量的准确性(合理即可).
若,方案仍然成立.
24.(1)①见解析;②,理由见解析;(2)
【分析】本题考查全等三角形的判定与性质;
(1)①证明即可得到;
②由(1)得,得到,即可证明,得到;
(2)由的面积为,,得到,由(1)可知,,则,再根据,得到,求出,最后根据求解即可.
【详解】证明:(1)① ∵平分,
∴,
∵,,
∴,
在和中,
,,,
∴,
∴;
② ;
理由:由(1)得,
∴,
∵, ,
∴,
∴;
(2)∵,
∴,
∴,
∵的面积为,,
∴,
解得,
由(1)可知,,
∴,
∵,
∴,即,
解得,
∴,
∴,
即种植鲜花的面积是.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列各图的中,正确画出边上的高的图形是( )
A. B.
C. D.
2.如图,,,,则的度数为( )
A. B. C. D.
3.如图,我们铁岭三中的电动伸缩校门利用的数学原理是( )
A.三角形的稳定性 B.四边形的不稳定性
C.两点之间线段最短 D.三角形两边之和大于第三边
4.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( )
A.SSS B.SAS C.AAS D.ASA
5.下列说法正确的是( )
A.到一个角两边距离相等的点在这个角的角平分线上
B.面积相等的两个三角形一定是全等三角形
C.两个等边三角形是全等三角形
D.有两条边对应相等的两个直角三角形全等
6.如图,三角形中,,,垂足为,则下列结论正确的是( )
A.点到的垂线段是线段 B.
C.点到的距离是线段的长度 D.
7.如图,表示两根长度相等的铁条,铁条的长度为.若O是的中点,,则容器的内径的长度是( )
A. B. C. D.
8.如图,已知,则等于( )
A. B. C. D.
9.如图,点E、F分别在菱形ABCD的BC、DC边上,添加以下条件不能证明△ABE≌△ADF的是( )
A.CE=CF B.∠BAF=∠DAE C.AE=AF D.∠AEC=∠AFC
10.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,.则AB的长可能是( )
A.3 B.4 C.7 D.11
11.如图,,是中,上的点,,,则下列结论:①,②,③,④,其中正确的有( )
A.个 B.个 C.个 D.个
12.如图,在中,,点D在边AC上,,且与关于直线BD对称.现有如下4个结论:①,②,③,④,其中正确的结论有( )
A.4 B.3个 C.2个 D.1个
二、填空题
13.如图,平分,.填空:因为平分,所以 .从而 .因此 .
14.平行四边形周长是40cm,则每条对角线长不能超过 cm.
15.如图,点在上,.请添加一个条件 ,使.
16.如图,已知EC=BC,∠1=∠2,要使△ECD≌△BCA,需添加的条件是 (只需写出一个条件).
17.a、b、c是等腰△ABC的三边长,其中a、b满足a2+b2﹣4a﹣10b+29=0,则△ABC的周长为 .
三、解答题
18.如图,,PC是的中线,,求:的度数.
解:∵PC是AB边上的中线,
∴__________(中线的定义)
在__________和__________中
∴____________________(________)
∴(______________________)
∵(已知)
∴(等量代换)
19.如图,和关于直线对称,与的交点在直线上.
(1)图中点的对应点是点 ,的对应角是 ;
(2)若,,则的长为 ;
(3)若,,求的度数.
20.如下图,已知,写出该组全等三角形的对应边和剩余的对应角.
21.如图,在边长为1个单位的正方形网格中,经过平移后得到,图中标出了点B的对应点.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
(1)画出;
(2)画出的高;
(3)连接、,那么与的关系是 ,线段AC扫过的图形的面积为 .
(4)在AB的右侧确定格点Q,使的面积和的面积相等,这样的Q点有 个.
22.已知:如图,,.
(1)AB与CD有怎样的位置关系?请证明你的结论.
(2)你还能发现哪些结论?
23.某中学七(2)班学生到户外活动,为了测量池塘两端A,B之间的距离,设计了如下方案:
如图,先过点B作的垂线,再在上取C,D两点,使,接着过点D作的垂线,交的延长线于点E,则测出的长即为点A,B之间的距离.
阅读后回答下列问题:
(1)此方案是否可行?请说明理由;
(2)方案中作的目的是什么?若,方案是否仍然成立(无须说明理由)?
24.【问题探究】
(1)如图①,在中,,的平分线交于点,于点.
①试说明:;
②如图②,点是线段上一点,连接,且,判断与之间的数量关系,并说明理由;
【问题解决】
(2)若图②中的是某市的一块空地,,和是三条小路(小路宽度忽略不计),现要在区域内种植鲜花,已知区域的面积为,,,求种植鲜花的面积(即的面积).
《第四章三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A D C B C C C
题号 11 12
答案 A A
1.B
【分析】本题考查了三角形的高,关键是利用基本作图作三角形高的方法解答.根据三角形的高的概念判断即可.
【详解】解:边上的高就是过顶点B作垂线段,垂直,交的延长线于D点,因此只有B符合条件,
故选:B.
2.B
【分析】在中由三角形内角和180°可求出,由全等三角形对应角相等可得即可求解.
【详解】解∶在中,,
∴
又∵,
∴,
故选B.
【点睛】本题考查三角形内角和与全等三角形的性质,熟记相应的概念是解题的关键.
3.B
【分析】本题考查了四边形的性质,根据电动伸缩门的工作原理,结合四边形的不稳定性即可得到答案,熟练掌握四边形的相关知识的解题的关键.
【详解】解:∵电动伸缩门的整体形状为四边形,且电动伸缩门的长度可以伸长和变短,
∴利用的数学原理是四边形的不稳定性,
故选:.
4.A
【分析】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键.
根据尺规作图可知,可证,得到,即可得到结论.
【详解】解:直尺和圆规作一个角等于已知角可得,
,
,
,
故选:A .
5.D
【分析】根据角平分线的判定可判断选项A错误,根据全等三角形的判定可判断选项B、C错误,选项D正确,即可得.
【详解】解:A、根据角平分线的判定“角的内部到角的两边的距离相等的点在角平分线上”,选项说法错误,不符合题意;
B、能够完全重合的两个三角形叫做全等三角形,选项说法错误,不符合题意;
C、两个等边三角形不是全等三角形,再有一条对应边相等才行,选项说法错误,不符合题意;
D、有两条边对应相等的两个直角三角形全等,选项说法正确,符合题意;
故选D.
【点睛】本题考查了角平分线,全等三角形的判定,解题的关键是掌握这些知识点.
6.C
【分析】根据三角形的三边关系和垂线段最短即可得到结论.
【详解】解:A、点到的垂线段是线段,故选项错误,不符合题意;
B、在中,是直角边,是斜边,故,故选项错误,不符合题意;
C、点到的距离是线段的长度,故选项正确,符合题意;
D、在中,和都是直角边,故,无法判断大小,故错误,不符合题意;
故选:C.
【点睛】本题考查了三角形的三边关系,垂线段最短,解题的关键是正确的识别图形.
7.B
【分析】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.只要证明,即可推出.
【详解】解:是的中点,,
在和中,
故选:B.
8.C
【分析】本题考查了平行线的性质和直角三角形两锐角互余的性质,掌握相关的性质是解题的关键.先根据平行线性质求出,再在直角三角形中利用直角三角形两锐角互余求出.
【详解】解:,
,
,
,
,
故选:C.
9.C
【分析】由四边形是菱形可得:,,再根据每个选项添加的条件逐一判断.
【详解】解:由四边形是菱形可得:,,
A、由CE=CF ,可得,可用证明,故不符合题意;
B、添加,可用证明,故不符合题意;
C、添加,不能证明,故符合题意;
D、由∠AEC=∠AFC ,可得,可用证明,故不符合题意;
故选:C.
【点睛】本题考查菱形性质及全等三角形的判定,解题的关键是掌握三角形全等的判定定理.
10.C
【分析】根据三角形三边关系定理,可知即可求解.
【详解】解:∵点与点关于点对称,点与点也关于点对称,
∴,
又∵∠AOD=∠BOC
∴△AOD≌△BOC(SAS)
∴AD=BC=3
∵
∴.
故选:C.
【点睛】本题考查了三角形三边关系定理:任意两边之和大于第三边,及对称的性质,全等三角形的判定与性质,解题的关键是将求AB的值转化为求三角形第三边的取值范围.
11.A
【分析】本题主要考查了全等三角形的性质,解题的关键是掌握全等三角形的对应角、对应边相等.根据全等三角形的性质,对每一项分别分析、解答出即可.
【详解】解:,
,,,,
故①④正确;
,
,,
,,
,
故②③正确;
综上,正确的有①②③④,共个,
故选:A.
12.A
【分析】根据等边对等角可得∠C=∠DBC,根据直角三角形两锐角互余和等角的余角相等可判断①;
根据折叠前后对应角相等和角的和差分别表示∠CBE和∠CDE,即可判断③;
代入到②④等式的左边与右边比较可判断②和④;
【详解】解:∵∠ABC=90°,
∴∠A+∠C=90°,∠ABD+∠DBC=90°,
∵BD=CD,
∴∠C=∠DBC,
∴∠ADB=∠DBC+∠C=2∠C,∠A=∠ABD,
∴AD=BD,即AC=AD+CD=2BD,①正确;
根据折叠的性质可知∠DBE=∠ABD,∠ADB=∠BDE,
∴∠DBE=∠ABD=∠A,∠ADB=∠BDE=2∠C,
∴∠CBE=2∠A-90°,∠CDE=180°-4∠C,
∴
,②正确;
∵,
∴,③正确;
∴,④正确;
综上所述,正确的有4个,
故选:A.
【点睛】本题考查三角形外角的性质,等边对等角,折叠问题,直角三角形两锐角互余等.解决此题的关键是熟练掌握定理,分别正确表示相应角.
13.
【分析】由AC平分∠DAB,∠1=∠2,可得出∠CAB=∠2,由内错角相等可以得出两直线平行.
【详解】解:∵AC平分∠DAB,
∴∠1=∠CAB.
又∵∠1=∠2,
∴∠CAB=∠2,
∴ABDC(内错角相等,两直线平行).
故答案为:∠CAB,∠CAB,DC.
【点睛】本题考查了平行线的判定定理以及角平分线的定义,解题的关键是找出∠CAB=∠2.解决该类题型只需牢牢掌握平行线的判定定理即可.
14.20
【分析】根据平行四边形的性质和三角形三边关系进行求解即可.
【详解】解:如图所示,平行四边形ABCD中,
,
在△ABD中,由三边关系知:,
∴,
同理可得,
即:每条对角线长不能超过20cm,
故答案为:20.
【点睛】本题考查平行四边形的性质以及三角形的三边关系,理解基本性质以及熟练综合运用基本结论是解题关键.
15.(答案不唯一)
【分析】本题考查了全等三角形的判定.根据已知条件中的一边一角,再添加一组对角相等即可.
【详解】解:∵,
再添加,
根据“角角边”就能证明.
故答案为:(答案不唯一).
16.DC=AC(答案不唯一)
【分析】由∠1=∠2可得∠ECD=∠BCA,再由EC=BC,添加DC=AC,利用“SAS”判定两个三角形全等.
【详解】解:添加的条件是DC=AC,理由如下:
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ECD=∠BCA,
在△ECD和△BCA中,
,
∴△ECD≌△BCA(SAS).
故答案为DC=AC.
【点睛】本题考查了全等三角形的判定定理.熟记全等三角形的判定定理是解题的关键.
17.12
【分析】先利用完全平方公式把a2+b2﹣4a﹣10b+29=0化为再利用非负数的性质求解 再分两种情况讨论:当为腰时,当为底时,结合三角形的三边关系,从而可得答案.
【详解】解: a2+b2﹣4a﹣10b+29=0,
a、b、c是等腰△ABC的三边长,
当为腰时,则另一腰 此时 三角形不存在,舍去,
当为底时,则腰 此时 三角形存在,
△ABC的周长为
故答案为:12
【点睛】本题考查的是利用完全平方公式分解因式,非负数的性质,三角形三边的关系,等腰三角形的定义,掌握以上基础知识是解题的关键.
18.见解析.
【分析】根据三角形中线的定义和全等三角形的判定与性质分别填空即可.
【详解】解:是边上的中线,
(中线的定义).
在和中,
,
,
(全等三角形对应角相等).
(已知),
(等量代换).
故答案为:,,,PB,BC,PC,PC,公共边,,,SSS,全等三角形对应角相等.
【点睛】本题考查了全等三角形的判定与性质,三角形中线的定义,主要是对逻辑推理能力的训练,熟记全等三角形的判定方法是解题的关键.
19.(1)E,
(2)3
(3)
【分析】本题主要考查了轴对称,成轴对称的两个图形的全等性:
(1)观察图形可直接得出答案;
(2)根据成轴对称的两个图形的全等性可得,根据全等三角形对应边相等即可求解;
(3)根据,,推出,根据对称性得到,推出.
【详解】(1)解:∵和关于直线对称,
∴图中点C的对应点是点E,的对应角是;
故答案为:E,.
(2)解:∵和关于直线对称,
∴,
∴,
∵,
∴.
故答案为:3.
(3)解:∵,,
∴,
根据对称性知,,
∴.
20.该组全等三角形的对应边为与与与,剩余的对应角为与.
【分析】本题考查了全等三角形的性质,根据全等三角形的对应边相等,对应角相等,即可作答.
【详解】解:∵,
∴该组全等三角形的对应边为与与与,剩余的对应角为与.
21.(1)
(2)见解析
(3),,10
(4)8
【分析】(1)分别作出,,的对应点,,即可.
(2)根据三角形高的定义画出图形即可.
(3)利用分割法求解即可.
(4)作关于的对称点,利用等高模型解决问题即可.
【详解】(1)如图,即为所求作.
(2)如图,线段即为所求作.
(3),,
线段扫过的图形的面积为.
故答案为:,,10
(4)满足条件的点有8个,
故答案为:8.
22.(1),证明见解析
(2),
【分析】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
(1),理由为:连接,由两直线平行内错角相等得到一对角相等,再由已知角相等及公共边,利用得到三角形全等,利用全等三角形对应边相等即可得证;
(2)还能得到与平行,.
【详解】(1)解:,理由如下:
连接,
,
,
在和中,
,
,
;
(2)还能确定出:,
23.(1)可行,见解析
(2)目的见解析,成立
【分析】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键:
(1)证明,可得到,故此方案可行.
(2)根据全等三角形的性质解答即可.
【详解】(1)解:此方案可行.理由如下:
由题意可知,,
所以.
在和中,
所以,
所以.
故此方案可行.
(2)作的目的是为了使,同时简化测量过程,提高测量的准确性(合理即可).
若,方案仍然成立.
24.(1)①见解析;②,理由见解析;(2)
【分析】本题考查全等三角形的判定与性质;
(1)①证明即可得到;
②由(1)得,得到,即可证明,得到;
(2)由的面积为,,得到,由(1)可知,,则,再根据,得到,求出,最后根据求解即可.
【详解】证明:(1)① ∵平分,
∴,
∵,,
∴,
在和中,
,,,
∴,
∴;
② ;
理由:由(1)得,
∴,
∵, ,
∴,
∴;
(2)∵,
∴,
∴,
∵的面积为,,
∴,
解得,
由(1)可知,,
∴,
∵,
∴,即,
解得,
∴,
∴,
即种植鲜花的面积是.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
