第六章变量之间的关系期末单元复习题(含解析)
文档属性
| 名称 | 第六章变量之间的关系期末单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 970.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 14:37:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六章变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某辆速度为的车从甲地开往相距的乙地,全程所用的时间为,在这个变化过程中,( )
A.是变量 B.是常量 C.是常量 D.是常量
2.质量P(P为整数)的对应关系如下表所示:
P(kg) 1 2 3 4 5 …
C(元) 2 2.5 3 3.5 4 …
则C与P之间的关系式为( )
A. B. C. D.
3.表中给出的统计数据,表示皮球从高度落下时与反弹到高度的关系:
40 50 60 80 100
25 30 35 45 55
用关系式表示y与x的这种关系正确的是( )
A. B. C. D.
4.某商店销售一批玩具时,其收入y(元)与销售数量x(个)之间有如下关系:
销售数量x(个) 1 2 3 4 ……
收入y(元) 8+0.3 16+0.6 24+0.9 32+1.2 ……
则收入y与销售数量x之间的关系式可表示为( )
A. B. C. D.
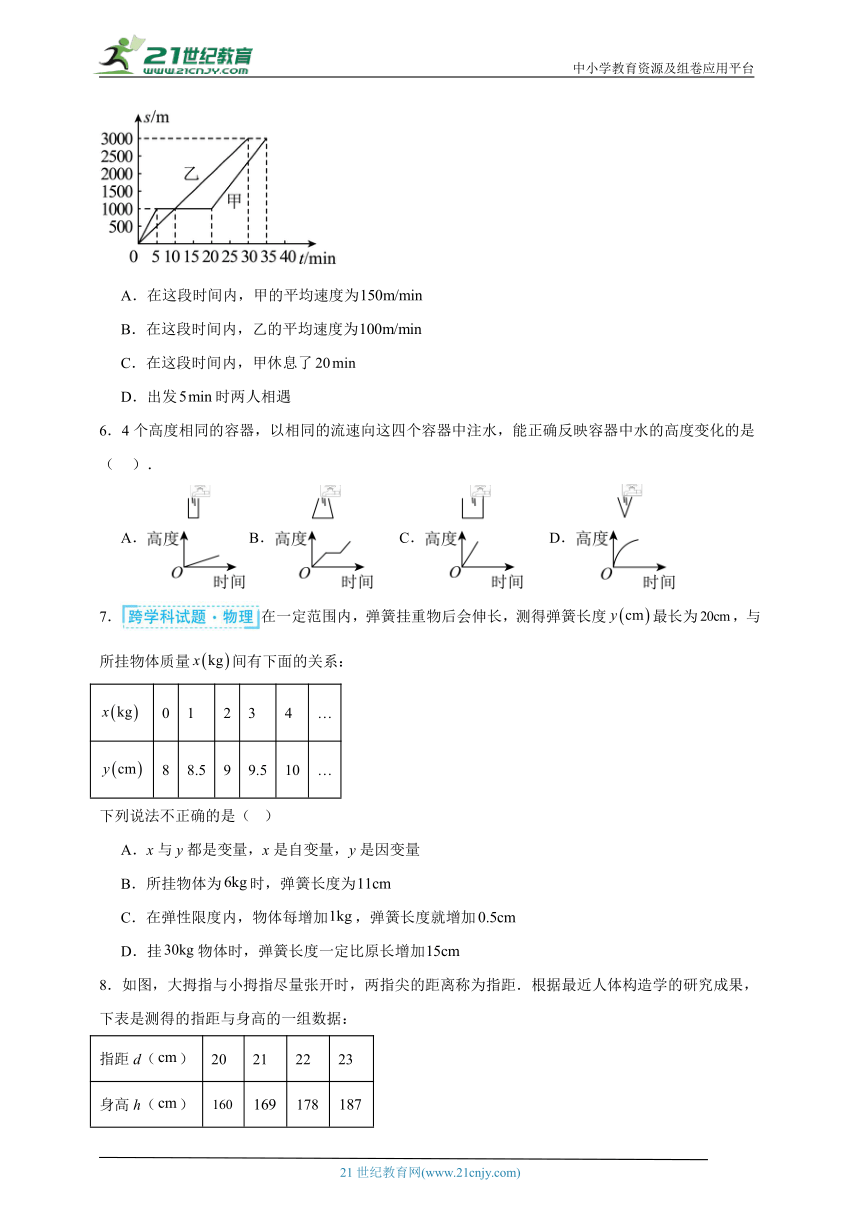
5.2023年5月21日,“锦绣太原·激情太马”2023太原马拉松赛成功举行,3.5万名选手沿汾河岸畔同场竞技,畅跑魅力并州.如图是甲、乙两人从起点出发一段时间内路程与时间的关系,则下列说法正确的是( )
A.在这段时间内,甲的平均速度为
B.在这段时间内,乙的平均速度为
C.在这段时间内,甲休息了
D.出发时两人相遇
6.4个高度相同的容器,以相同的流速向这四个容器中注水,能正确反映容器中水的高度变化的是( ).
A. B. C. D.
7.在一定范围内,弹簧挂重物后会伸长,测得弹簧长度最长为,与所挂物体质量间有下面的关系:
0 1 2 3 4 …
8 8.5 9 9.5 10 …
下列说法不正确的是( )
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为时,弹簧长度为
C.在弹性限度内,物体每增加,弹簧长度就增加
D.挂物体时,弹簧长度一定比原长增加
8.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果,下表是测得的指距与身高的一组数据:
指距d() 20 21 22 23
身高h()
已知,世界上被证实最高的人的身高是厘米,则他的指距约为( )
A. B. C. D.
9.某学习小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
温度 0 10 20 30
声速 318 324 330 336 342 348
下列说法中错误的是( )
A.在这个变化过程中,自变量是温度,因变量是声速
B.在一定范围内,温度越高,声速越快
C.当空气温度为时,内声音可以传播
D.在一定范围内,温度每升高,声速增加
10.弹簧的受力和伸长量成正比.某次实验中,小军组的同学们记录了同一根弹簧的长度y(cm)和所挂物体质量x(kg)(0≤x≤12)的对应数据如下表(部分)所示,下列说法中正确的是( )
x(kg) 0 1 2 3 4 ...
y(cm) 10.5 11 11.5 12 ...
A.x,y都是变量,y是x的正比例函数
B.当所挂物体的质量为10kg时,弹簧长度是19cm
C.物体质量由4 kg增加到7kg,弹簧的长度增加1cm
D.弹簧不挂物体时的长度是10cm
11.某市出租车收费标准如下表:设行驶里程数为,收费为y元,则y与x()之间的关系式为( )
里程数 收费/元
3以下(含3) 8
3以上每增加1 1.8
A. B. C. D.
二、填空题
12.一辆汽车在行驶的过程中,已知汽车行驶的速度是60千米/小时,若设x小时行驶的路程为y千米,那么变量y与x之间的关系式为 .
13.高山地区海拔高,空气稀薄,所以大气压低于一个标准大气压,水的沸点随高原气压的减小而降低.下表是各个城市的海拔高度及水的沸点统计情况,请根据表中的大致数据,推断地水的沸点为 .
城市 地 地 地 地 地
海拔(米 0 300 600 1500
沸点(度 100 99 98
14.表格中列出了一个试验的统计数据,表示皮球从高处落下时,弹跳高度与下降高度的关系.给出下列关系式:①;②;③;④.其中能表示这种关系的是 .(填序号)
15.变量x,y的一些对应值如表:
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
根据表格中的数据规律,当时,y的值是 .
16.等腰三角形顶角度数随底角度数的变化而变化.若设底角为,顶角为,则y与x的关系式为 .
三、解答题
17.某公交车司机统计了月乘车人数x(人)与月利润y(元)的部分数据如下表,假设每位乘客的公交票价固定不变,公交车月支出费用为6000元.(月利润=月收入-月支出费用)
x(人) … 2500 2750 3000 3500 4000 …
y(元) … -1000 -500 0 1000 2000 …
(1)根据函数的定义,y是关于x的函数吗?
(2)结合表格解答下列问题:
①公交车票的单价是多少元?
②当x=2750时,y的值是多少?它的实际意义是什么?
18.如图所示,梯形上底的长是,下底长,高.
(1)梯形面积与上底之间的关系式是什么;
(2)当x每增加时,y如何变化?
(3)当时,y等于什么?此时y表示的是什么?
19.如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车匀速行驶了______分钟,时速是______千米/时;
(2)汽车在行驶途中在哪段时间停车休息?休息了多长时间?
(3)若司机从第28分钟开始先匀速行驶8分钟后,立即减速行驶2分钟,至停止.请你按照以上叙述在途中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
20.下图是某水库的库容曲线图,其中x表示水库的平均水深(m),表示水库的库容(万).根据图象回答下面的问题:
(1)这个函数反映了哪两个变量之间的关系?
(2)填表:
5 10 15 20 25
V(万)
(3)当平均水深取至之间的一个确定的值时,相应的库容确定吗?
(4)库容V可以看成平均水深x的函数吗?
(5)求当时的函数值,并说明它的实际意义.
21.兴平市南市镇的苹果种植历史悠久,以红富士为主,种植规模达到万亩,深秋,这里的苹果迎来丰收,鲜红透亮,饱满圆润.鲜上鲜水果店刘老板购进一批红富士苹果销售,售价为每千克9元,如果一次购买4千克以上的这种苹果,超过4千克的部分按售价的七五折售卖.设(元)表示付款金额,(千克)表示购买的质量.
(1)求出与之间的关系式;(提示:分两种情况)
(2)隔壁的水果店也销售同样品质的这种苹果,售价为每千克9元,且全部按售价的八五折售卖.李阿姨和王阿姨分别在这两个水果店购买苹果,结果付款金额与购买苹果的质量都一样,那么她们各自买了多少千克苹果?各自花了多少钱?
22.某公交车每月的支出费用为4000元,每月的乘车人数(人)与每月利润(利润=收入费用-支出费用)(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(人) 500 1000 1500 2000 2500 3000 ……
(元) -3000 -2000 -1000 0 1000 2000 ……
(1)在这个变化过程中,______是自变量,______是因变量;(填中文)
(2)观察表中数据可知,每月乘客量达到______人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为_______元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达_______人.
23.如图1,两地之间有一条笔直的道路,地位于两地之间,甲从地出发驾车驶往地,乙从地出发驾车驶向地.在行驶过程中,乙由于汽车故障,换乘客车(换乘时间忽略不计)继续前行,并与甲同时到达地.图2中线段和折线段分别表示甲、乙两人与地的距离与甲行驶的时间的变化关系,其中与交于点.
(1)在图2中表示的变量是______,因变量是______;
(2)乙比甲晚出发______,两地相距______;
(3)请直接写出甲的速度为______;
(4)______,______;
(5)在图2中点表示的含义是______;
(6)请直接写出当______时,甲、乙相距.
《第六章变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D A B D D B C D
题号 11
答案 D
1.D
【分析】根据常量、变量的定义结合具体问题情境进行判断即可.
【详解】解:某辆速度为的车从甲地开往相距的乙地,全程所用的时间为,在这个变化过程中,
速度为与所用的时间为是变量,甲乙两地的距离是常量,
故选:D.
【点睛】本题考查常量与变量,理解常量与变量的定义是正确判断的前提.常量就是在变化过程中不变的量,变量就是可以取到不同数值的量.
2.D
【分析】根据表可以得到增加1,则对应的C增加,据此即可求解.
【详解】解:根据表可以得到增加1,则对应的C增加,则C与P之间的关系式为.
故选:D
【点睛】此题考查了函数关系式,找到规律“增加1,则对应的C增加”是解题的关键.
3.D
【分析】本题主要考查了函数的表示法,分析表格中的数据得出x每增加10,y增加5,从表格中的数据得出规律,求出函数解析式即可.
【详解】解:由表格中的数据可知,当x每增加10,y增加5,
∵,
,
,
,
,
∴.
故选:D.
4.A
【分析】根据表格中、、和时,的值进行归纳类推即可得.
【详解】解:由表格可知,当时,,
当时,,
当时,,
当时,,
所以收入与销售数量之间的关系式可表示为,即,
故选:A.
【点睛】本题考查了用表格表示变量间的关系、用关系式表示变量间的关系,正确观察出表格中列出的两个变量的对应值之间的关系是解题关键.
5.B
【分析】根据速度=路程÷时间结合图象可求出甲、乙的平均速度;根据时甲的路程没有改变可知此时甲在休息,然后可得休息的时间;甲、乙图象交点的横坐标即是两人相遇的时间,问题得解.
【详解】解:A. 甲的平均速度为,说法错误,不符合题意;
B. 乙的平均速度为,说法正确,符合题意;
C. 甲休息了,说法错误,不符合题意;
D. 由函数图象得,出发时两人相遇,说法错误,不符合题意,
故选:B.
【点睛】本题考查了从图象获取信息的能力,正确理解横纵坐标所表示的意义是解题的关键.
6.D
【分析】本题主要考查了折线统计图,根据容器的形状,判断出水面升高的高度随时间变化的规律,逐项进行判断即可.
【详解】解:AC.因为水流速度相同,A选项中容器的底面积较小,C选项中容器的底面积较大,所以向A容器中注水时,高度随时间变化的较快,向A容器中注水时,高度随时间变化的较慢,故AC错误;
B.因为容器越向上横截面积越小,所以高度随时间变化的越来越快,故B错误;
D.因为容器越向上横截面积越大,所以高度随时间变化的越来越慢,故D正确.
故选:D.
7.D
【分析】本题考查了变量、自变量、因变量的概念,认真审题能从题目中抽取出有效信息是解题的关键.弹簧长度随所挂物体的重量的变化而变化,由表格数据可知物体每增加,弹簧长度就增加,可以计算当所挂物体为或时弹簧的长度,但应注意弹簧的最大长度为.
【详解】解:A.因为弹簧长度随所挂物体的重量的变化而变化,所以x是自变量,y是因变量.故本选项正确,不符合题意;
B.当所挂物体为时,弹簧的长度为.故本选项正确,不符合题意;
C.从表格数据中分析可知,物体每增加,弹簧长度就增加.故本选项正确,不符合题意;
D.当所挂物体为时,弹簧长度为.故本选项不正确,符合题意.
故选:D.
8.B
【分析】本题考查了用表格表示函数关系,根据表格可知,指距每增加身高就增加,据此列式计算即可求出答案.
【详解】解:根据表格可知,指距每增加身高就增加,
,
即世界上被证实最高的人的身高是厘米,则他的指距约为,
故选:B.
9.C
【分析】本题主要考查了函数的表示方法和有理数的混合运算.根据图表里的信息,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【详解】解:A. 在这个变化过程中,自变量是温度,因变量是声速,正确,此选项不符合题意;
B.根据数据表可知,在一定范围内,温度越高,声速越快,正确,此选项不符合题意;
C、,当空气温度为时,声音可以传播,故选项不符合题意;
D、∵,,,,,
∴当温度每升高,声速增加,正确,此选项不符合题意;
故选:C.
10.D
【分析】根据图表数据可得,弹簧的长度随所挂重物的质量的变化而变化,并且质量每增加1千克,弹簧的长度增加0.5cm,先求出一次函数的解析式,然后对各选项分析判断后利用排除法.
【详解】解:A、x,y都是变量,y是x的一次函数;故A错误;
设一次函数的解析式为,结合表格的数据可得:
,解得,
∴;
B、当所挂物体的质量为10kg时,弹簧长度是cm;故B错误;
C、物体质量4 kg时弹簧长度是cm;
物体质量7kg时,弹簧的长度是cm,
∴增加了cm;故C错误;
D、弹簧不挂物体时的长度是10cm,故D正确;
故选:D
【点睛】本题考查了求一次函数的解析式,函数关系的确认,常量与变量的确定,读懂图表数据,并从表格数据得出正确结论是解题的关键,是基础题,难度不大.
11.D
【分析】本题考查了函数的关系式,审题是解题的关键.
根据3以下(含3)收费8元,3以上每增加1米收费1.8元,列出关系式即可.
【详解】解:由题意得,所付车费为:,
即.
故选:D.
12.
【分析】本题主要考查函数关系式.根据路程速度时间,即可得出答案.
【详解】解:由题意得.
故答案为:.
13.95度
【分析】本题考查了函数关系式,发现表格中两个变量对应值的变化规律是解题的关键.根据表格中两个变量变化关系可知,海拔每增加,沸点就降低1度,由此得解.
【详解】解:由表格中两个变量对应值的变化规律可知,海拔每增加,沸点就降低1度,
即,
当,地水的沸点(度.
故答案为:95度.
14.②
【分析】本题考查求函数关系式,根据表格即可得到,关系即可得到答案;
【详解】解:由表格可得,
∵,,,,
∴,
故答案为:②.
15.-125
【分析】根据表格中两个变量对应值的变化规律得出答案.
【详解】解:由表格中两个变量对应值的变化规律可知,y=x3,
当x=﹣5时,y=(﹣5)3=﹣125,
故答案为:﹣125.
【点睛】本题考查了用表格表示变量间的关系,发现表格中两个变量对应值的变化规律是解题的关键.
16.
【分析】本题考查了三角形的内角和定理、等腰三角形的性质、利用关系式表示函数关系,熟练掌握三角形的内角和定理和等腰三角形的性质是解题关键.先根据三角形的内角和定理可得,再根据等腰三角形的性质可得的取值范围,由此即可得.
【详解】解:由题意得:,
则,
∵等腰三角形的底角为,
∴,
所以与的关系式为,
故答案为:.
17.(1)y是关于x的函数,理由见详解
(2)①2元;②当x=2750时,函数值y=-500,实际意义是:月乘车人数为2750人时,公交车本月亏损500元.
【分析】(1)根据函数的定义:在一个变化过程中,因变量随着自变量的变化而变化,对于每一个确定的自变量都有唯一确定的因变量与之对应,进行解答即可;
(2)结合表格进行解答即可.
【详解】(1)解:根据函数的定义可知:y是关于x的函数.
(2)解:①由题意得:
公交车票价:6000÷3000=2(元).
②当x=2750时,函数值y=-500,
实际意义是:月乘车人数为2750人时,公交车本月亏损500元.
【点睛】本题考查函数的定义,以及用表格法表示函数.理解函数的定义是解题的关键.
18.(1)
(2)当x每增加时,y增加
(3)当时,,此时y表示的是的面积
【分析】本题主要考查了列函数关系式,求函数值:
(1)根据梯形面积计算公式求解即可;
(2)根据(1)所求求出当时,当时的函数值即可得到答案;
(3)根据(1)所求求出当时的值,根据可得点A和点D重合,则此时y表示的是的面积.
【详解】(1)解:由题意得:;
(2)解:当时,,
当时,,
∵,
∴当x每增加时,y增加;
(3)解:当时,,此时y表示的是的面积.
19.(1)4,45
(2)汽车在行驶途中,在分钟这个时间段停车休息,休息了6分钟
(3)见解析
【分析】(1)直接由图象知汽车在段匀速行驶,进而可得结论;
(2)直接由图知,汽车在段的速度为0,进而可求解;
(3)根据题中描述补画图象即可.
【详解】(1)解:由图知,汽车匀速行驶了(分钟),时速是45千米/时,
故答案为:4,45;
(2)解:由图可知,汽车在段的速度为0,所以汽车在行驶途中,在分钟这个时间段停车休息,休息了(分钟).
(3)解:如图所示:
【点睛】本题考查用图象表示变量间的关系,理解题意,从图象上获取所需信息是解答的关键.
20.(1)水库的库容与平均水深之间的关系.
(2)10,40,75,150,250
(3)确定
(4)是
(5)当时的函数值为,表示的意义是:当水库的平均水深为18m时,水库的库容是125万.
【分析】(1)观察水库的库容曲线图,理解横、纵坐标代表的实际意义,就可解答问题;
(2)从图象可以读出来即可;
(3)抓住函数的概念,就可以判断出来;
(4)抓住函数的概念,就可以判断出来;
(5)从图象可以读出来,还要结合横、纵坐标代表的实际意义,即可解答.
【详解】(1)根据图像可知,这个函数反映了水库的库容与平均水深之间的关系.
(2)根据图像可知,
5 10 15 20 25
V(万) 10 40 75 150 250
故答案为:10,40,75,150,250;
(3)根据图像可知,当平均水深取至之间的一个确定的值时,相应的库容确定;
(4)根据函数图像及函数定义可知,库容V可以看成平均水深x的函数;
(5)根据图像可知,当时的函数值为,
表示的意义是:当水库的平均水深为18m时,水库的库容是125万.
【点睛】本题考查的是由图象反映的信息来解决的题目,解此类题的关键是理解点的横坐标和纵坐标的实际意义,明确点的坐标与点的对应关系,培养观察能力和分析问题的能力,体现了数形结合的思想,将“数”和“形”结合在一起研究、探索,从而解决问题.函数的三种表示形式是:列表法、图象法、解析法.本题考查的是图象法.
21.(1)
(2)她们各自买了10千克苹果?各自花了元
【分析】本题主要考查了列函数关系式,一元一次方程的应用,
(1)分和,两种情况根据所给苹果价格方案列式求解即可;
(2)当时,李阿姨需付款元,王阿姨需要付款元,则在购买了苹果的前提下,两位阿姨的付款金额不可能相同,故,则,解方程即可得到答案.
【详解】(1)解:当时,;
当时,;
∴;
(2)解:当时,李阿姨需付款元,王阿姨需要付款元,
∴在购买了苹果的前提下,两位阿姨的付款金额不可能相同,
∴,
∴,
解得,
∴,
答:她们各自买了10千克苹果?各自花了元.
22.(1)每月的乘车人数,每月利润;(2)2000;(3)3000;(4)4500.
【分析】(1)直接利用常量与变量的定义分析即可得答案;
(2)直接利用表中数据分析得出答案;
(3)利用由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,进而得出答案;
(4)由(3)得出当利润为5000元时乘客人数,即可得出答案.
【详解】(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
(2)∵观察表中数据可知,当每月乘客量达到2000人以上时,每月利润为0,
∴每月乘客量达到2000人以上时,该公交车才不会亏损;
(3)∵每月乘客量增加500人时,每月利润增加1000元,
∴当每月乘车人数为3500人时,每月利润为3000元;
(4)∵每月乘客量增加500人时,每月利润增加1000元,
∴若5月份想获得利润5000元,5月份的乘客量需达4500人.
【点睛】本题主要考查了常量与变量以及函数的表示方法,正确把握函数的定义是解题关键.
23.(1)甲行驶的时间;甲、乙两人与地的距离
(2)
(3)
(4)
(5)乙出发后(或甲出发后)两人相遇,相遇地点距地
(6)或或14
【分析】本题考查了函数的图象,从图象上获取信息,求出甲乙两人的速度是正确解答的关键.
(1)根据函数的定义解答即可;
(2)由图象可得乙比甲晚出发两地相距(千米);
(3)根据点的坐标可求出甲,乙两人的驾车速度;
(4)根据两车的速度可得答案;
(5)根据点的坐标解答即可;
(6)分两种情况,①时,②时,分别列方程求解即可.
【详解】(1)解:在图2中表示的自变量是甲行驶的时间,因变量是甲、乙两人与地的距离;
故答案为:甲行驶的时间;甲、乙两人与地的距离;
(2)解:由图象可知,乙比甲晚出发的是两地相距(千米);
故答案为:;
(3)解:甲的驾车速度为:;
故答案为:;
(4)解:由题意可得,,
乙的驾车速度为:,
所以,
故答案为:;
(5)解:在图2中点表示的含义是乙出发后(或甲出发后)两人相遇,相遇地点距地;
故答案为:乙出发后(或甲出发后)两人相遇,相遇地点距地;
(6)解:分两种情况,①时,
,
解得:,
②时,
乙的速度为,
∴,
∴,
综上,当或6.5或14时,甲,乙相距.
故答案为:或或14.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某辆速度为的车从甲地开往相距的乙地,全程所用的时间为,在这个变化过程中,( )
A.是变量 B.是常量 C.是常量 D.是常量
2.质量P(P为整数)的对应关系如下表所示:
P(kg) 1 2 3 4 5 …
C(元) 2 2.5 3 3.5 4 …
则C与P之间的关系式为( )
A. B. C. D.
3.表中给出的统计数据,表示皮球从高度落下时与反弹到高度的关系:
40 50 60 80 100
25 30 35 45 55
用关系式表示y与x的这种关系正确的是( )
A. B. C. D.
4.某商店销售一批玩具时,其收入y(元)与销售数量x(个)之间有如下关系:
销售数量x(个) 1 2 3 4 ……
收入y(元) 8+0.3 16+0.6 24+0.9 32+1.2 ……
则收入y与销售数量x之间的关系式可表示为( )
A. B. C. D.
5.2023年5月21日,“锦绣太原·激情太马”2023太原马拉松赛成功举行,3.5万名选手沿汾河岸畔同场竞技,畅跑魅力并州.如图是甲、乙两人从起点出发一段时间内路程与时间的关系,则下列说法正确的是( )
A.在这段时间内,甲的平均速度为
B.在这段时间内,乙的平均速度为
C.在这段时间内,甲休息了
D.出发时两人相遇
6.4个高度相同的容器,以相同的流速向这四个容器中注水,能正确反映容器中水的高度变化的是( ).
A. B. C. D.
7.在一定范围内,弹簧挂重物后会伸长,测得弹簧长度最长为,与所挂物体质量间有下面的关系:
0 1 2 3 4 …
8 8.5 9 9.5 10 …
下列说法不正确的是( )
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为时,弹簧长度为
C.在弹性限度内,物体每增加,弹簧长度就增加
D.挂物体时,弹簧长度一定比原长增加
8.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果,下表是测得的指距与身高的一组数据:
指距d() 20 21 22 23
身高h()
已知,世界上被证实最高的人的身高是厘米,则他的指距约为( )
A. B. C. D.
9.某学习小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
温度 0 10 20 30
声速 318 324 330 336 342 348
下列说法中错误的是( )
A.在这个变化过程中,自变量是温度,因变量是声速
B.在一定范围内,温度越高,声速越快
C.当空气温度为时,内声音可以传播
D.在一定范围内,温度每升高,声速增加
10.弹簧的受力和伸长量成正比.某次实验中,小军组的同学们记录了同一根弹簧的长度y(cm)和所挂物体质量x(kg)(0≤x≤12)的对应数据如下表(部分)所示,下列说法中正确的是( )
x(kg) 0 1 2 3 4 ...
y(cm) 10.5 11 11.5 12 ...
A.x,y都是变量,y是x的正比例函数
B.当所挂物体的质量为10kg时,弹簧长度是19cm
C.物体质量由4 kg增加到7kg,弹簧的长度增加1cm
D.弹簧不挂物体时的长度是10cm
11.某市出租车收费标准如下表:设行驶里程数为,收费为y元,则y与x()之间的关系式为( )
里程数 收费/元
3以下(含3) 8
3以上每增加1 1.8
A. B. C. D.
二、填空题
12.一辆汽车在行驶的过程中,已知汽车行驶的速度是60千米/小时,若设x小时行驶的路程为y千米,那么变量y与x之间的关系式为 .
13.高山地区海拔高,空气稀薄,所以大气压低于一个标准大气压,水的沸点随高原气压的减小而降低.下表是各个城市的海拔高度及水的沸点统计情况,请根据表中的大致数据,推断地水的沸点为 .
城市 地 地 地 地 地
海拔(米 0 300 600 1500
沸点(度 100 99 98
14.表格中列出了一个试验的统计数据,表示皮球从高处落下时,弹跳高度与下降高度的关系.给出下列关系式:①;②;③;④.其中能表示这种关系的是 .(填序号)
15.变量x,y的一些对应值如表:
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
根据表格中的数据规律,当时,y的值是 .
16.等腰三角形顶角度数随底角度数的变化而变化.若设底角为,顶角为,则y与x的关系式为 .
三、解答题
17.某公交车司机统计了月乘车人数x(人)与月利润y(元)的部分数据如下表,假设每位乘客的公交票价固定不变,公交车月支出费用为6000元.(月利润=月收入-月支出费用)
x(人) … 2500 2750 3000 3500 4000 …
y(元) … -1000 -500 0 1000 2000 …
(1)根据函数的定义,y是关于x的函数吗?
(2)结合表格解答下列问题:
①公交车票的单价是多少元?
②当x=2750时,y的值是多少?它的实际意义是什么?
18.如图所示,梯形上底的长是,下底长,高.
(1)梯形面积与上底之间的关系式是什么;
(2)当x每增加时,y如何变化?
(3)当时,y等于什么?此时y表示的是什么?
19.如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车匀速行驶了______分钟,时速是______千米/时;
(2)汽车在行驶途中在哪段时间停车休息?休息了多长时间?
(3)若司机从第28分钟开始先匀速行驶8分钟后,立即减速行驶2分钟,至停止.请你按照以上叙述在途中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
20.下图是某水库的库容曲线图,其中x表示水库的平均水深(m),表示水库的库容(万).根据图象回答下面的问题:
(1)这个函数反映了哪两个变量之间的关系?
(2)填表:
5 10 15 20 25
V(万)
(3)当平均水深取至之间的一个确定的值时,相应的库容确定吗?
(4)库容V可以看成平均水深x的函数吗?
(5)求当时的函数值,并说明它的实际意义.
21.兴平市南市镇的苹果种植历史悠久,以红富士为主,种植规模达到万亩,深秋,这里的苹果迎来丰收,鲜红透亮,饱满圆润.鲜上鲜水果店刘老板购进一批红富士苹果销售,售价为每千克9元,如果一次购买4千克以上的这种苹果,超过4千克的部分按售价的七五折售卖.设(元)表示付款金额,(千克)表示购买的质量.
(1)求出与之间的关系式;(提示:分两种情况)
(2)隔壁的水果店也销售同样品质的这种苹果,售价为每千克9元,且全部按售价的八五折售卖.李阿姨和王阿姨分别在这两个水果店购买苹果,结果付款金额与购买苹果的质量都一样,那么她们各自买了多少千克苹果?各自花了多少钱?
22.某公交车每月的支出费用为4000元,每月的乘车人数(人)与每月利润(利润=收入费用-支出费用)(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(人) 500 1000 1500 2000 2500 3000 ……
(元) -3000 -2000 -1000 0 1000 2000 ……
(1)在这个变化过程中,______是自变量,______是因变量;(填中文)
(2)观察表中数据可知,每月乘客量达到______人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为_______元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达_______人.
23.如图1,两地之间有一条笔直的道路,地位于两地之间,甲从地出发驾车驶往地,乙从地出发驾车驶向地.在行驶过程中,乙由于汽车故障,换乘客车(换乘时间忽略不计)继续前行,并与甲同时到达地.图2中线段和折线段分别表示甲、乙两人与地的距离与甲行驶的时间的变化关系,其中与交于点.
(1)在图2中表示的变量是______,因变量是______;
(2)乙比甲晚出发______,两地相距______;
(3)请直接写出甲的速度为______;
(4)______,______;
(5)在图2中点表示的含义是______;
(6)请直接写出当______时,甲、乙相距.
《第六章变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D A B D D B C D
题号 11
答案 D
1.D
【分析】根据常量、变量的定义结合具体问题情境进行判断即可.
【详解】解:某辆速度为的车从甲地开往相距的乙地,全程所用的时间为,在这个变化过程中,
速度为与所用的时间为是变量,甲乙两地的距离是常量,
故选:D.
【点睛】本题考查常量与变量,理解常量与变量的定义是正确判断的前提.常量就是在变化过程中不变的量,变量就是可以取到不同数值的量.
2.D
【分析】根据表可以得到增加1,则对应的C增加,据此即可求解.
【详解】解:根据表可以得到增加1,则对应的C增加,则C与P之间的关系式为.
故选:D
【点睛】此题考查了函数关系式,找到规律“增加1,则对应的C增加”是解题的关键.
3.D
【分析】本题主要考查了函数的表示法,分析表格中的数据得出x每增加10,y增加5,从表格中的数据得出规律,求出函数解析式即可.
【详解】解:由表格中的数据可知,当x每增加10,y增加5,
∵,
,
,
,
,
∴.
故选:D.
4.A
【分析】根据表格中、、和时,的值进行归纳类推即可得.
【详解】解:由表格可知,当时,,
当时,,
当时,,
当时,,
所以收入与销售数量之间的关系式可表示为,即,
故选:A.
【点睛】本题考查了用表格表示变量间的关系、用关系式表示变量间的关系,正确观察出表格中列出的两个变量的对应值之间的关系是解题关键.
5.B
【分析】根据速度=路程÷时间结合图象可求出甲、乙的平均速度;根据时甲的路程没有改变可知此时甲在休息,然后可得休息的时间;甲、乙图象交点的横坐标即是两人相遇的时间,问题得解.
【详解】解:A. 甲的平均速度为,说法错误,不符合题意;
B. 乙的平均速度为,说法正确,符合题意;
C. 甲休息了,说法错误,不符合题意;
D. 由函数图象得,出发时两人相遇,说法错误,不符合题意,
故选:B.
【点睛】本题考查了从图象获取信息的能力,正确理解横纵坐标所表示的意义是解题的关键.
6.D
【分析】本题主要考查了折线统计图,根据容器的形状,判断出水面升高的高度随时间变化的规律,逐项进行判断即可.
【详解】解:AC.因为水流速度相同,A选项中容器的底面积较小,C选项中容器的底面积较大,所以向A容器中注水时,高度随时间变化的较快,向A容器中注水时,高度随时间变化的较慢,故AC错误;
B.因为容器越向上横截面积越小,所以高度随时间变化的越来越快,故B错误;
D.因为容器越向上横截面积越大,所以高度随时间变化的越来越慢,故D正确.
故选:D.
7.D
【分析】本题考查了变量、自变量、因变量的概念,认真审题能从题目中抽取出有效信息是解题的关键.弹簧长度随所挂物体的重量的变化而变化,由表格数据可知物体每增加,弹簧长度就增加,可以计算当所挂物体为或时弹簧的长度,但应注意弹簧的最大长度为.
【详解】解:A.因为弹簧长度随所挂物体的重量的变化而变化,所以x是自变量,y是因变量.故本选项正确,不符合题意;
B.当所挂物体为时,弹簧的长度为.故本选项正确,不符合题意;
C.从表格数据中分析可知,物体每增加,弹簧长度就增加.故本选项正确,不符合题意;
D.当所挂物体为时,弹簧长度为.故本选项不正确,符合题意.
故选:D.
8.B
【分析】本题考查了用表格表示函数关系,根据表格可知,指距每增加身高就增加,据此列式计算即可求出答案.
【详解】解:根据表格可知,指距每增加身高就增加,
,
即世界上被证实最高的人的身高是厘米,则他的指距约为,
故选:B.
9.C
【分析】本题主要考查了函数的表示方法和有理数的混合运算.根据图表里的信息,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【详解】解:A. 在这个变化过程中,自变量是温度,因变量是声速,正确,此选项不符合题意;
B.根据数据表可知,在一定范围内,温度越高,声速越快,正确,此选项不符合题意;
C、,当空气温度为时,声音可以传播,故选项不符合题意;
D、∵,,,,,
∴当温度每升高,声速增加,正确,此选项不符合题意;
故选:C.
10.D
【分析】根据图表数据可得,弹簧的长度随所挂重物的质量的变化而变化,并且质量每增加1千克,弹簧的长度增加0.5cm,先求出一次函数的解析式,然后对各选项分析判断后利用排除法.
【详解】解:A、x,y都是变量,y是x的一次函数;故A错误;
设一次函数的解析式为,结合表格的数据可得:
,解得,
∴;
B、当所挂物体的质量为10kg时,弹簧长度是cm;故B错误;
C、物体质量4 kg时弹簧长度是cm;
物体质量7kg时,弹簧的长度是cm,
∴增加了cm;故C错误;
D、弹簧不挂物体时的长度是10cm,故D正确;
故选:D
【点睛】本题考查了求一次函数的解析式,函数关系的确认,常量与变量的确定,读懂图表数据,并从表格数据得出正确结论是解题的关键,是基础题,难度不大.
11.D
【分析】本题考查了函数的关系式,审题是解题的关键.
根据3以下(含3)收费8元,3以上每增加1米收费1.8元,列出关系式即可.
【详解】解:由题意得,所付车费为:,
即.
故选:D.
12.
【分析】本题主要考查函数关系式.根据路程速度时间,即可得出答案.
【详解】解:由题意得.
故答案为:.
13.95度
【分析】本题考查了函数关系式,发现表格中两个变量对应值的变化规律是解题的关键.根据表格中两个变量变化关系可知,海拔每增加,沸点就降低1度,由此得解.
【详解】解:由表格中两个变量对应值的变化规律可知,海拔每增加,沸点就降低1度,
即,
当,地水的沸点(度.
故答案为:95度.
14.②
【分析】本题考查求函数关系式,根据表格即可得到,关系即可得到答案;
【详解】解:由表格可得,
∵,,,,
∴,
故答案为:②.
15.-125
【分析】根据表格中两个变量对应值的变化规律得出答案.
【详解】解:由表格中两个变量对应值的变化规律可知,y=x3,
当x=﹣5时,y=(﹣5)3=﹣125,
故答案为:﹣125.
【点睛】本题考查了用表格表示变量间的关系,发现表格中两个变量对应值的变化规律是解题的关键.
16.
【分析】本题考查了三角形的内角和定理、等腰三角形的性质、利用关系式表示函数关系,熟练掌握三角形的内角和定理和等腰三角形的性质是解题关键.先根据三角形的内角和定理可得,再根据等腰三角形的性质可得的取值范围,由此即可得.
【详解】解:由题意得:,
则,
∵等腰三角形的底角为,
∴,
所以与的关系式为,
故答案为:.
17.(1)y是关于x的函数,理由见详解
(2)①2元;②当x=2750时,函数值y=-500,实际意义是:月乘车人数为2750人时,公交车本月亏损500元.
【分析】(1)根据函数的定义:在一个变化过程中,因变量随着自变量的变化而变化,对于每一个确定的自变量都有唯一确定的因变量与之对应,进行解答即可;
(2)结合表格进行解答即可.
【详解】(1)解:根据函数的定义可知:y是关于x的函数.
(2)解:①由题意得:
公交车票价:6000÷3000=2(元).
②当x=2750时,函数值y=-500,
实际意义是:月乘车人数为2750人时,公交车本月亏损500元.
【点睛】本题考查函数的定义,以及用表格法表示函数.理解函数的定义是解题的关键.
18.(1)
(2)当x每增加时,y增加
(3)当时,,此时y表示的是的面积
【分析】本题主要考查了列函数关系式,求函数值:
(1)根据梯形面积计算公式求解即可;
(2)根据(1)所求求出当时,当时的函数值即可得到答案;
(3)根据(1)所求求出当时的值,根据可得点A和点D重合,则此时y表示的是的面积.
【详解】(1)解:由题意得:;
(2)解:当时,,
当时,,
∵,
∴当x每增加时,y增加;
(3)解:当时,,此时y表示的是的面积.
19.(1)4,45
(2)汽车在行驶途中,在分钟这个时间段停车休息,休息了6分钟
(3)见解析
【分析】(1)直接由图象知汽车在段匀速行驶,进而可得结论;
(2)直接由图知,汽车在段的速度为0,进而可求解;
(3)根据题中描述补画图象即可.
【详解】(1)解:由图知,汽车匀速行驶了(分钟),时速是45千米/时,
故答案为:4,45;
(2)解:由图可知,汽车在段的速度为0,所以汽车在行驶途中,在分钟这个时间段停车休息,休息了(分钟).
(3)解:如图所示:
【点睛】本题考查用图象表示变量间的关系,理解题意,从图象上获取所需信息是解答的关键.
20.(1)水库的库容与平均水深之间的关系.
(2)10,40,75,150,250
(3)确定
(4)是
(5)当时的函数值为,表示的意义是:当水库的平均水深为18m时,水库的库容是125万.
【分析】(1)观察水库的库容曲线图,理解横、纵坐标代表的实际意义,就可解答问题;
(2)从图象可以读出来即可;
(3)抓住函数的概念,就可以判断出来;
(4)抓住函数的概念,就可以判断出来;
(5)从图象可以读出来,还要结合横、纵坐标代表的实际意义,即可解答.
【详解】(1)根据图像可知,这个函数反映了水库的库容与平均水深之间的关系.
(2)根据图像可知,
5 10 15 20 25
V(万) 10 40 75 150 250
故答案为:10,40,75,150,250;
(3)根据图像可知,当平均水深取至之间的一个确定的值时,相应的库容确定;
(4)根据函数图像及函数定义可知,库容V可以看成平均水深x的函数;
(5)根据图像可知,当时的函数值为,
表示的意义是:当水库的平均水深为18m时,水库的库容是125万.
【点睛】本题考查的是由图象反映的信息来解决的题目,解此类题的关键是理解点的横坐标和纵坐标的实际意义,明确点的坐标与点的对应关系,培养观察能力和分析问题的能力,体现了数形结合的思想,将“数”和“形”结合在一起研究、探索,从而解决问题.函数的三种表示形式是:列表法、图象法、解析法.本题考查的是图象法.
21.(1)
(2)她们各自买了10千克苹果?各自花了元
【分析】本题主要考查了列函数关系式,一元一次方程的应用,
(1)分和,两种情况根据所给苹果价格方案列式求解即可;
(2)当时,李阿姨需付款元,王阿姨需要付款元,则在购买了苹果的前提下,两位阿姨的付款金额不可能相同,故,则,解方程即可得到答案.
【详解】(1)解:当时,;
当时,;
∴;
(2)解:当时,李阿姨需付款元,王阿姨需要付款元,
∴在购买了苹果的前提下,两位阿姨的付款金额不可能相同,
∴,
∴,
解得,
∴,
答:她们各自买了10千克苹果?各自花了元.
22.(1)每月的乘车人数,每月利润;(2)2000;(3)3000;(4)4500.
【分析】(1)直接利用常量与变量的定义分析即可得答案;
(2)直接利用表中数据分析得出答案;
(3)利用由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,进而得出答案;
(4)由(3)得出当利润为5000元时乘客人数,即可得出答案.
【详解】(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
(2)∵观察表中数据可知,当每月乘客量达到2000人以上时,每月利润为0,
∴每月乘客量达到2000人以上时,该公交车才不会亏损;
(3)∵每月乘客量增加500人时,每月利润增加1000元,
∴当每月乘车人数为3500人时,每月利润为3000元;
(4)∵每月乘客量增加500人时,每月利润增加1000元,
∴若5月份想获得利润5000元,5月份的乘客量需达4500人.
【点睛】本题主要考查了常量与变量以及函数的表示方法,正确把握函数的定义是解题关键.
23.(1)甲行驶的时间;甲、乙两人与地的距离
(2)
(3)
(4)
(5)乙出发后(或甲出发后)两人相遇,相遇地点距地
(6)或或14
【分析】本题考查了函数的图象,从图象上获取信息,求出甲乙两人的速度是正确解答的关键.
(1)根据函数的定义解答即可;
(2)由图象可得乙比甲晚出发两地相距(千米);
(3)根据点的坐标可求出甲,乙两人的驾车速度;
(4)根据两车的速度可得答案;
(5)根据点的坐标解答即可;
(6)分两种情况,①时,②时,分别列方程求解即可.
【详解】(1)解:在图2中表示的自变量是甲行驶的时间,因变量是甲、乙两人与地的距离;
故答案为:甲行驶的时间;甲、乙两人与地的距离;
(2)解:由图象可知,乙比甲晚出发的是两地相距(千米);
故答案为:;
(3)解:甲的驾车速度为:;
故答案为:;
(4)解:由题意可得,,
乙的驾车速度为:,
所以,
故答案为:;
(5)解:在图2中点表示的含义是乙出发后(或甲出发后)两人相遇,相遇地点距地;
故答案为:乙出发后(或甲出发后)两人相遇,相遇地点距地;
(6)解:分两种情况,①时,
,
解得:,
②时,
乙的速度为,
∴,
∴,
综上,当或6.5或14时,甲,乙相距.
故答案为:或或14.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
