第六章平行四边形期末单元复习题(含解析)
文档属性
| 名称 | 第六章平行四边形期末单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章平行四边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在腰长为的等腰中,,,,分别是,,上的点,并且,,则四边形的周长是( )
A. B. C. D.
2.一个四边形四个内角的度数之比为 ,则该四边形最小内角的度数为( )
A.75° B.70° C.65° D.60°
3.如图,在四边形中,,若,则的度数是( )
A. B. C. D.
4.将一个n边形变成(n+1)边形,内角和将( )
A.减少180° B.增加90° C.增加180° D.增加360°
5.如图,,,,垂足为 A,,垂足为D.下面四个结论:①;②;③;④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
6.在平面直角坐标系中,平行四边形的边在轴上,顶点,,对角线、相交于点、分别以点、为圆心,以大于长为半径画弧,两弧交于点,连接交于点,则点的横坐标为( ).
A.5 B.4 C.3 D.1
7.在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AE, 则∠BAD等于 ( )
A.120° B.135° C.130° D.不能确定
8.如图,将平行四边形沿对角线折叠,使点落在点处,若,,则的度数为( ).
A.124° B.114° C.104° D.56°
9.不能作为正多边形的内角的度数的是( )
A.120° B.108° C.144° D.145°
10.如果一个正多边形的每个外角是,则这个正多边形的对角线共有( )条.
A.8 B.9 C. D.
11.如图,在中,,的平分线分别交于点E,F,若,,则EF的长是( )
A.2 B.2.5 C.3 D.3.5
12.如图,折叠ABCD,使折痕经过点B,交AD边于点E,点C落在BA延长线上的点G处,点D落在点H处,得到四边形AEHG.若ABCD的面积是8,则下列结论中正确的是( )
A.四边形AEHG不是平行四边形
B.AB≠AE
C.设四边形AEHG的面积为y,四边形BCDE的面积为x,则y与x的函数关系式是
D.若BC=4,则点E到BG的距离为1
二、填空题
13.如图,,,,,都在上.(1)图中圆内接四边形的外角是 ;(2)的内对角是 .
14.如图,顺次连接四边形四边的中点,则四边形的形状一定是 .
15.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是 .
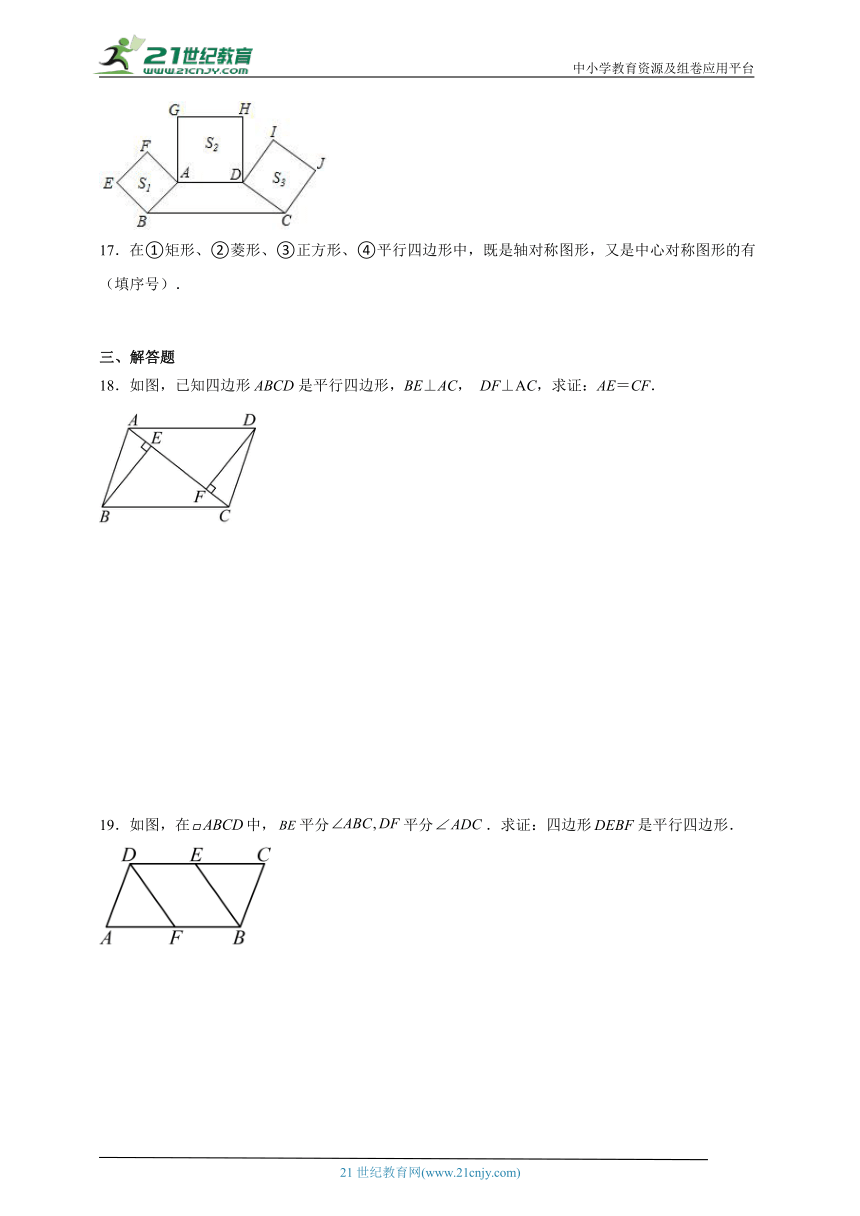
16.如图,四边形ABCD中,AD∥BC,且∠B+∠C=90°,分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI,且其面积依次记为S1、S2、S3,若S1+S3=4S2,则= .
17.在①矩形、②菱形、③正方形、④平行四边形中,既是轴对称图形,又是中心对称图形的有 (填序号).
三、解答题
18.如图,已知四边形ABCD是平行四边形,BE⊥AC, DF⊥AC,求证:AE=CF.
19.如图,在中,平分平分.求证:四边形是平行四边形.
20.如图,在平行四边形ABCD中,点M是边AD上的点,连接MB,MC,点N为BC边上的动点,点E,F为MB,MC上的两点,连接NE,NF,且∠BNE=∠CMD,∠BEN=∠NFC.求证:四边形MENF为平行四边形.
21.求出下列图中的x值.
22.如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=105°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请直接写出α,β所满足的数量关系式;
(3)如图2,若α=β,判断BE,DF的位置关系,并说明理由.
23.如图所示,已知四边形ABCD是平行四边形,在AB的延长线上截取BE=AB,BF=BD,连接CE,DF,相交于点M.求证:CD=CM.
24.平行四边形中,点O是对角线中点,点E在边上,的延长线与边交于点F,连接 ,如图1.
(1)求证:四边形是平行四边形;
(2)在(1)中,若,过点C作的垂线,与 分别交于点G H R,如图2
①当时时,求的长.
②探究与的数量关系,直接写出答案.
《第六章平行四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B C A C B A D B
题号 11 12
答案 A C
1.D
【分析】本题考查了平行四边形的性质与判定,等腰三角形的性质与判定,熟练掌握平行四边形的性质与判定是解题的关键.根据题意得出四边形是平行四边形,进而根据等边对等角以及平行线的性质,得,得出,则,进而根据平行四边形的性质,即可求解.
【详解】解:∵,,
∴四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴平行四边形的周长为:.
故选:D.
2.D
【分析】根据题意:可设这四个内角分别为:x,x, ,x,再根据四边形的内角和为 ,可求出x的值,即可求解.
【详解】解:根据题意:可设这四个内角分别为:x,x, ,x,
∵四边形的内角和为 ,
∴ ,
解得:
∴最小内角的度数为: .
故选:D.
【点睛】本题主要考查了四边形的内角和,熟练掌握四边形的内角和为360度是解题的关键.
3.B
【分析】本题考查了平行四边形的性质和判定,熟练掌握平行四边形的性质和判定是解题的关键.
证明四边形是平行四边形,根据平行四边形的性质即可得到结论.
【详解】解:∵,
∴四边形是平行四边形,
∵,
,
故选:B.
4.C
【分析】利用多边形的内角和公式即可求出答案.
【详解】解:n边形的内角和是(n﹣2) 180°,
n+1边形的内角和是(n﹣1) 180°,
因而(n+1)边形的内角和比n边形的内角和大(n﹣1) 180°﹣(n﹣2) 180=180°.
故选C.
5.A
【分析】本题考查平行线间距离,三角形和四边形平移性质,平行四边形判定及性质等.根据题意逐一对序号进行分析即可得到本题答案.
【详解】解:∵,,,,
∴四边形和四边形均为平行四边形,
∴,,,,
∴向右平移即可得到,
∴,
∵平行四边形和平行四边形有公共边和公共的高,
∴,
∴①②③④都正确,
故选:A.
6.C
【分析】连接,根据作图得到垂直平分线段,从而得到,设,在中利用勾股定理列出方程得出,即可得出点的横坐标
【详解】∵四边形是平行四边形,∴为对角线中点,
由作图可知,垂直平分线段,
连接,则,
延长交轴于点,则轴,
∵,,平行四边形
∴OC=AB=6,AM=2,OM=4
设,则,
在中,有,
解得,,
∴ME=3
∴点的横坐标为3.
故选:C.
【点睛】本题考查了基本作图、线段垂直平分线的性质、平行四边形的性质,勾股定理,得出AE=1是解本题的关键.
7.B
【详解】解:过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B.
8.A
【分析】根据折叠、平行四边形的性质,三角形的内角和定理,即可求出答案.
【详解】解:
由折叠得,,
∵四边形是平行四边形,
∴,
∴,
∴,
又∵,
∴,
在中,,
故选:A.
【点睛】本题考查折叠的性质、平行四边形的性质,三角形的内角和定理等知识,由图形直观得出各个角之间的关系是正确解答的关键.
9.D
【详解】试题分析:设边数为n(n为大于等于3的整数),根据正多边形各个内角相等和多边形的内角和公式建立方程,求出n,进行判断即可.
A、(n-2) 180=120 n,解得n=6,所以A选项错误;
B、(n-2) 180=108 n,解得n=5,所以B选项错误;
C、(n-2) 180=144 n,解得n=10,所以C选项错误;
D、(n-2) 180=145 n,解得n=,不为整数,所以D选项正确.
故选D.
10.B
【分析】本题考查多边形内角与外角.解题的关键在于掌握正多边形的外角和为,并且正多边形的每一个外角都相等.
根据正多边形的每一个外角都相等,多边形的边数=,进而求得多边形的对角线条数.
【详解】解:这个正多边形的边数:,
则对角线的条数是:,
故选:B.
11.A
【分析】根据平行四边形的性质证明DF=CD,AE=AB,进而可得AF和ED的长,然后可得答案.
【详解】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB=CD=3,AD=BC=4,
∴∠DFC=∠FCB,
又∵CF平分∠BCD,
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC=3,
同理可证:AE=AB=3,
∴AF=DE
∵AD=4,
∴AF=4-3=1,
∴EF=4-1-1=2.
故选:A.
【点睛】本题主要考查了平行四边形的性质,解题的关键是掌握在平行四边形中,当出现角平分线时,一般可利用等腰三角形的性质解题.
12.C
【分析】根据轴对称、平行四边形、等腰三角形的性质,得,,从而证明四边形AEHG是平行四边形;根据轴对称和平行四边形的性质,得;设点E到BG的距离为,结合根据轴对称的性质分析,即可得到答案.
【详解】解:∵折叠ABCD,使折痕经过点B,交AD边于点E,点C落在BA延长线上的点G处,点D落在点H处,
∴,,,四边形面积=四边形面积
∵ABCD
∴,,
∴,
∴,
∴,即选项B不正确;
∴
∴四边形AEHG是平行四边形,即选项A不正确;
∴
∵四边形面积=四边形面积
∴四边形面积=+四边形AEHG面积
∵四边形AEHG的面积为y,四边形BCDE的面积为x,ABCD的面积是8
∴,即
∵点E在AD边上
∴四边形BCDE面积,即
∴,即选项C正确;
设点E到BG的距离为
∵四边形面积
∴四边形面积
∴,即
∴
∴,即点E到BG的距离为2
∴选项D不正确
故选:C.
【点睛】本题考查了一次函数、平行四边形、等腰三角形、轴对称的知识;解题的关键是熟练掌握轴对称、平行四边形的性质,从而完成求解.
13. (1)∠DBG; (2)∠AED.
【分析】根据圆内接四边形外角的定义和内对角的定义即可得到答案.
【详解】由图可知,根据圆内接四边形外角的定义可得图中圆内接四边形的外角是为∠DBG;因为的邻补角为,所以的内对角是∠AED.
【点睛】本题考查圆内接四边形外角的定义和内对角的定义,解题的关键是熟练掌握圆内接四边形外角的定义和内对角的定义.
14.平行四边形
【分析】顺次连接任意四边形四边中点所得的四边形,由三角形中位线的性质可得一组对边平行且相等,再根据平行四边形的判定进行判断即可.
【详解】如图,连接,
∵分别是四边形边的中点,
∴,
∴且
∴四边形是平行四边形,
故答案为:平行四边形.
【点睛】本题考查了三角形中位线的性质,平行四边形的判定,熟练掌握知识点是解题的关键.
15.6
【详解】解:根据多边形的外角和等于360°和正多边形的每一个外角都相等,得多边形的边数为360°÷60°=6.
故答案为:6.
16.3
【分析】过点A作AE∥BC交CD于点E,得到平行四边形ABCE和Rt△ADE,根据平行四边形的性质和勾股定理,不难证明三个正方形的边长对应等于所得直角三角形的边.
【详解】解:过点A作AE∥DC交CB于点E,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴AD=CE,DC=AE,∠BCD=∠AEB,
∵∠ABC+∠BCD=90°,
∴∠ABC+∠AEB=90°,
∴∠BAE=90°,
在Rt△ABE中,AB2+AE2=BE2,
∵S1=AB2,S2=AD2=BE2,S3=DC2=AE2,
∵S1+S3=4S2,
∴AB2+DC2=AB2+AE2=4AD2=BE2,
∴,
∴.
故答案为:3.
【点睛】本题主要考查了平行四边形的判定和性质、勾股定理,准确计算是解题的关键.
17.①②③
【详解】矩形、菱形、正方形既是轴对称图形,又是中心对称图形.
平行四边形是中心对称图形,但不是轴对称图形.
故答案为:①②③
18.见解析
【分析】可证明ABECDF,即可得到结论.
【详解】证明:∵四边形ABCD是平行四边形
∴AB=CD,ABCD
∴∠BAC=∠DCA
∵BEAC于E,DFAC于F
∴∠AEB=∠DFC=90°
在ABE和CDF中 ,
∴ABECDF(AAS)
∴AE=CF
【点睛】此题考查平行四边形的性质和全等三角形的判定及性质,掌握平行四边形的性质和全等三角形的判定是解决问题的关键.
19.见解析
【分析】本题考查平行四边形的判定和性质,根据平行四边形的性质得到,,根据角平分线的性质,结合平行线的性质,得到,进而得到,结合,即可得证.
【详解】证明:∵四边形是平行四边形,
∴,.
∵平分,平分,
∴,,
∴.
∵,
∴.
∴.
∴.
又∵,即,
∴四边形是平行四边形.
20.证明见解析
【分析】只需要分别证明ENMC,NFMB,即可证明四边形MENF为平行四边形.
【详解】证明:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠MCB=∠CMD,
∵∠BNE=∠CMD,
∴∠BNE=∠MCB,
∴ENMC,
∴∠NFC=∠ENF,
∵∠BEN=∠NFC,
∴∠BEN=∠ENF,
∴NFMB,
∴四边形MENF为平行四边形.
【点睛】本题主要考查了平行四边形的性质与判定,熟知平行四边形的性质与判定条件是解题的关键.
21.65;60.
【分析】先求出多边形的内角和,然后再利用方程求得未知数的值.
【详解】解:由四边形的内角和为360°,
则有:150°+80°+2x°=360°,解得x=65
由五边形内角和为:180°×(5-2)=540°,
则有:3x°+160°+90°+110°=540°,解得x=60
故答案为:65,60.
【点睛】本题考查了运用多边形内角和定理求多边形的内角的大小,解题关键在于求得多边形内角和,即多边形内角和=180°×(n-2)(n为多边形的边数).
22.(1)105°
(2)β-α=90°
(3)BE∥DF,理由见解析
【分析】(1)利用四边形的内角和和平角的定义推导即可;
(2)利用角平分线的定义,四边形的内角和以及三角形的内角和转化即可;
(3)利用角平分线的定义以及平行线的判定与性质即可解答.
【详解】(1)解:∵四边形ABCD的内角和为360°,
∴α+β=∠A+∠BCD=360°-(∠ABC+∠ADC),
∵∠MBC和∠NDC是四边形ABCD的外角,
∴∠MBC=180°-∠ABC,∠NDC=180°-∠ADC,
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC
=360°-(∠ABC+∠ADC),
=α+β
=105°;
(2)解:β-α=90°(或α-β=-90°等均正确).
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG= ∠MBC,∠CDG= ∠NDC,
∴∠CBG+∠CDG= ∠MBC+ ∠NDC= (∠MBC+∠NDC)= (α+β),
在△BCD中,∠BDC+∠CBD=180°-∠BCD=180°-β,
在△BDG中,∠BGD=45°,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(α+β)+180°-β+45°=180°,
∴β-α=90°.
故答案为β-α=90°(或α-β=-90°等均正确);
(3)解:BE∥DF.
理由:如图2,过点C作CP∥BE,
则∠EBC=∠BCP,
∴∠DCP=∠BCD-∠BCP=β-∠EBC,
由(1)知∠MBC+∠NDC=α+β,
∵α=β,
∴∠MBC+∠NDC=2β,
又∵BE、DF分别平分∠MBC和∠NDC,
∴∠EBC+∠FDC=(∠MBC+∠NDC)=β,
∴∠FDC=β-∠EBC,
又∵∠DCP=β-∠EBC,
∴∠FDC=∠DCP,
∴CP∥DF,
又CP∥BE,
∴BE∥DF.
【点睛】此题主要考查了平行线的性质及其判定、平角的定义,四边形的内角和,三角形内角和,角平分线的定义,用整体代换的思想是解本题的关键,整体思想是初中阶段的一种重要思想,要多加强训练.
23.详见解析
【分析】利用一组对边平行且相等得到四边形BDCE是平行四边形,然后利用对边平行得到两组角相等,进而整理到∠CDF=∠CMD,进而得证.
【详解】证明:∵四边形ABCD是平行四边形.
∴ABDC.
又∵BE=AB,
∴BEDC,
∴四边形BDCE是平行四边形.
∴DC∥BF,BD∥CE,
∴∠CDF=∠F,∠BDM=∠DMC.
∵BD=BF,
∴∠BDF=∠F.
∴∠CDF=∠CMD,
∴CD=CM.
【点睛】本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.当证明两条在一个三角形中的边相等时,通常是利用等角对等边来进行证明.
24.(1)见解析
(2)①;②
【分析】本题是四边形综合题,考查了平行四边形的性质,全等三角形的判定和性质,勾股定理,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.
(1)由可得,可得,可得结论;
(2)①由等腰三角形的性质可得由勾股定理可求,由等腰三角形的性质可求的长,即可求解;
②如图,过点H作于点M,证明,可得,由等腰直角三角形的性质可得,即可得结论.
【详解】(1)证明:∵平行四边形中,点O是对角线中点,
∴,
∴,且,
∴,
∴,且,
∴四边形是平行四边形;
(2)①如图2,过点D作点N,
∵,,
∴,
∴,
∵,
∴,
∴,
∴;
②,
理由如下:如图,过点H作于点M,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴
∴,且,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章平行四边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在腰长为的等腰中,,,,分别是,,上的点,并且,,则四边形的周长是( )
A. B. C. D.
2.一个四边形四个内角的度数之比为 ,则该四边形最小内角的度数为( )
A.75° B.70° C.65° D.60°
3.如图,在四边形中,,若,则的度数是( )
A. B. C. D.
4.将一个n边形变成(n+1)边形,内角和将( )
A.减少180° B.增加90° C.增加180° D.增加360°
5.如图,,,,垂足为 A,,垂足为D.下面四个结论:①;②;③;④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
6.在平面直角坐标系中,平行四边形的边在轴上,顶点,,对角线、相交于点、分别以点、为圆心,以大于长为半径画弧,两弧交于点,连接交于点,则点的横坐标为( ).
A.5 B.4 C.3 D.1
7.在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AE, 则∠BAD等于 ( )
A.120° B.135° C.130° D.不能确定
8.如图,将平行四边形沿对角线折叠,使点落在点处,若,,则的度数为( ).
A.124° B.114° C.104° D.56°
9.不能作为正多边形的内角的度数的是( )
A.120° B.108° C.144° D.145°
10.如果一个正多边形的每个外角是,则这个正多边形的对角线共有( )条.
A.8 B.9 C. D.
11.如图,在中,,的平分线分别交于点E,F,若,,则EF的长是( )
A.2 B.2.5 C.3 D.3.5
12.如图,折叠ABCD,使折痕经过点B,交AD边于点E,点C落在BA延长线上的点G处,点D落在点H处,得到四边形AEHG.若ABCD的面积是8,则下列结论中正确的是( )
A.四边形AEHG不是平行四边形
B.AB≠AE
C.设四边形AEHG的面积为y,四边形BCDE的面积为x,则y与x的函数关系式是
D.若BC=4,则点E到BG的距离为1
二、填空题
13.如图,,,,,都在上.(1)图中圆内接四边形的外角是 ;(2)的内对角是 .
14.如图,顺次连接四边形四边的中点,则四边形的形状一定是 .
15.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是 .
16.如图,四边形ABCD中,AD∥BC,且∠B+∠C=90°,分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI,且其面积依次记为S1、S2、S3,若S1+S3=4S2,则= .
17.在①矩形、②菱形、③正方形、④平行四边形中,既是轴对称图形,又是中心对称图形的有 (填序号).
三、解答题
18.如图,已知四边形ABCD是平行四边形,BE⊥AC, DF⊥AC,求证:AE=CF.
19.如图,在中,平分平分.求证:四边形是平行四边形.
20.如图,在平行四边形ABCD中,点M是边AD上的点,连接MB,MC,点N为BC边上的动点,点E,F为MB,MC上的两点,连接NE,NF,且∠BNE=∠CMD,∠BEN=∠NFC.求证:四边形MENF为平行四边形.
21.求出下列图中的x值.
22.如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
(1)如图1,若α+β=105°,求∠MBC+∠NDC的度数;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请直接写出α,β所满足的数量关系式;
(3)如图2,若α=β,判断BE,DF的位置关系,并说明理由.
23.如图所示,已知四边形ABCD是平行四边形,在AB的延长线上截取BE=AB,BF=BD,连接CE,DF,相交于点M.求证:CD=CM.
24.平行四边形中,点O是对角线中点,点E在边上,的延长线与边交于点F,连接 ,如图1.
(1)求证:四边形是平行四边形;
(2)在(1)中,若,过点C作的垂线,与 分别交于点G H R,如图2
①当时时,求的长.
②探究与的数量关系,直接写出答案.
《第六章平行四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B C A C B A D B
题号 11 12
答案 A C
1.D
【分析】本题考查了平行四边形的性质与判定,等腰三角形的性质与判定,熟练掌握平行四边形的性质与判定是解题的关键.根据题意得出四边形是平行四边形,进而根据等边对等角以及平行线的性质,得,得出,则,进而根据平行四边形的性质,即可求解.
【详解】解:∵,,
∴四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴平行四边形的周长为:.
故选:D.
2.D
【分析】根据题意:可设这四个内角分别为:x,x, ,x,再根据四边形的内角和为 ,可求出x的值,即可求解.
【详解】解:根据题意:可设这四个内角分别为:x,x, ,x,
∵四边形的内角和为 ,
∴ ,
解得:
∴最小内角的度数为: .
故选:D.
【点睛】本题主要考查了四边形的内角和,熟练掌握四边形的内角和为360度是解题的关键.
3.B
【分析】本题考查了平行四边形的性质和判定,熟练掌握平行四边形的性质和判定是解题的关键.
证明四边形是平行四边形,根据平行四边形的性质即可得到结论.
【详解】解:∵,
∴四边形是平行四边形,
∵,
,
故选:B.
4.C
【分析】利用多边形的内角和公式即可求出答案.
【详解】解:n边形的内角和是(n﹣2) 180°,
n+1边形的内角和是(n﹣1) 180°,
因而(n+1)边形的内角和比n边形的内角和大(n﹣1) 180°﹣(n﹣2) 180=180°.
故选C.
5.A
【分析】本题考查平行线间距离,三角形和四边形平移性质,平行四边形判定及性质等.根据题意逐一对序号进行分析即可得到本题答案.
【详解】解:∵,,,,
∴四边形和四边形均为平行四边形,
∴,,,,
∴向右平移即可得到,
∴,
∵平行四边形和平行四边形有公共边和公共的高,
∴,
∴①②③④都正确,
故选:A.
6.C
【分析】连接,根据作图得到垂直平分线段,从而得到,设,在中利用勾股定理列出方程得出,即可得出点的横坐标
【详解】∵四边形是平行四边形,∴为对角线中点,
由作图可知,垂直平分线段,
连接,则,
延长交轴于点,则轴,
∵,,平行四边形
∴OC=AB=6,AM=2,OM=4
设,则,
在中,有,
解得,,
∴ME=3
∴点的横坐标为3.
故选:C.
【点睛】本题考查了基本作图、线段垂直平分线的性质、平行四边形的性质,勾股定理,得出AE=1是解本题的关键.
7.B
【详解】解:过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B.
8.A
【分析】根据折叠、平行四边形的性质,三角形的内角和定理,即可求出答案.
【详解】解:
由折叠得,,
∵四边形是平行四边形,
∴,
∴,
∴,
又∵,
∴,
在中,,
故选:A.
【点睛】本题考查折叠的性质、平行四边形的性质,三角形的内角和定理等知识,由图形直观得出各个角之间的关系是正确解答的关键.
9.D
【详解】试题分析:设边数为n(n为大于等于3的整数),根据正多边形各个内角相等和多边形的内角和公式建立方程,求出n,进行判断即可.
A、(n-2) 180=120 n,解得n=6,所以A选项错误;
B、(n-2) 180=108 n,解得n=5,所以B选项错误;
C、(n-2) 180=144 n,解得n=10,所以C选项错误;
D、(n-2) 180=145 n,解得n=,不为整数,所以D选项正确.
故选D.
10.B
【分析】本题考查多边形内角与外角.解题的关键在于掌握正多边形的外角和为,并且正多边形的每一个外角都相等.
根据正多边形的每一个外角都相等,多边形的边数=,进而求得多边形的对角线条数.
【详解】解:这个正多边形的边数:,
则对角线的条数是:,
故选:B.
11.A
【分析】根据平行四边形的性质证明DF=CD,AE=AB,进而可得AF和ED的长,然后可得答案.
【详解】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB=CD=3,AD=BC=4,
∴∠DFC=∠FCB,
又∵CF平分∠BCD,
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC=3,
同理可证:AE=AB=3,
∴AF=DE
∵AD=4,
∴AF=4-3=1,
∴EF=4-1-1=2.
故选:A.
【点睛】本题主要考查了平行四边形的性质,解题的关键是掌握在平行四边形中,当出现角平分线时,一般可利用等腰三角形的性质解题.
12.C
【分析】根据轴对称、平行四边形、等腰三角形的性质,得,,从而证明四边形AEHG是平行四边形;根据轴对称和平行四边形的性质,得;设点E到BG的距离为,结合根据轴对称的性质分析,即可得到答案.
【详解】解:∵折叠ABCD,使折痕经过点B,交AD边于点E,点C落在BA延长线上的点G处,点D落在点H处,
∴,,,四边形面积=四边形面积
∵ABCD
∴,,
∴,
∴,
∴,即选项B不正确;
∴
∴四边形AEHG是平行四边形,即选项A不正确;
∴
∵四边形面积=四边形面积
∴四边形面积=+四边形AEHG面积
∵四边形AEHG的面积为y,四边形BCDE的面积为x,ABCD的面积是8
∴,即
∵点E在AD边上
∴四边形BCDE面积,即
∴,即选项C正确;
设点E到BG的距离为
∵四边形面积
∴四边形面积
∴,即
∴
∴,即点E到BG的距离为2
∴选项D不正确
故选:C.
【点睛】本题考查了一次函数、平行四边形、等腰三角形、轴对称的知识;解题的关键是熟练掌握轴对称、平行四边形的性质,从而完成求解.
13. (1)∠DBG; (2)∠AED.
【分析】根据圆内接四边形外角的定义和内对角的定义即可得到答案.
【详解】由图可知,根据圆内接四边形外角的定义可得图中圆内接四边形的外角是为∠DBG;因为的邻补角为,所以的内对角是∠AED.
【点睛】本题考查圆内接四边形外角的定义和内对角的定义,解题的关键是熟练掌握圆内接四边形外角的定义和内对角的定义.
14.平行四边形
【分析】顺次连接任意四边形四边中点所得的四边形,由三角形中位线的性质可得一组对边平行且相等,再根据平行四边形的判定进行判断即可.
【详解】如图,连接,
∵分别是四边形边的中点,
∴,
∴且
∴四边形是平行四边形,
故答案为:平行四边形.
【点睛】本题考查了三角形中位线的性质,平行四边形的判定,熟练掌握知识点是解题的关键.
15.6
【详解】解:根据多边形的外角和等于360°和正多边形的每一个外角都相等,得多边形的边数为360°÷60°=6.
故答案为:6.
16.3
【分析】过点A作AE∥BC交CD于点E,得到平行四边形ABCE和Rt△ADE,根据平行四边形的性质和勾股定理,不难证明三个正方形的边长对应等于所得直角三角形的边.
【详解】解:过点A作AE∥DC交CB于点E,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴AD=CE,DC=AE,∠BCD=∠AEB,
∵∠ABC+∠BCD=90°,
∴∠ABC+∠AEB=90°,
∴∠BAE=90°,
在Rt△ABE中,AB2+AE2=BE2,
∵S1=AB2,S2=AD2=BE2,S3=DC2=AE2,
∵S1+S3=4S2,
∴AB2+DC2=AB2+AE2=4AD2=BE2,
∴,
∴.
故答案为:3.
【点睛】本题主要考查了平行四边形的判定和性质、勾股定理,准确计算是解题的关键.
17.①②③
【详解】矩形、菱形、正方形既是轴对称图形,又是中心对称图形.
平行四边形是中心对称图形,但不是轴对称图形.
故答案为:①②③
18.见解析
【分析】可证明ABECDF,即可得到结论.
【详解】证明:∵四边形ABCD是平行四边形
∴AB=CD,ABCD
∴∠BAC=∠DCA
∵BEAC于E,DFAC于F
∴∠AEB=∠DFC=90°
在ABE和CDF中 ,
∴ABECDF(AAS)
∴AE=CF
【点睛】此题考查平行四边形的性质和全等三角形的判定及性质,掌握平行四边形的性质和全等三角形的判定是解决问题的关键.
19.见解析
【分析】本题考查平行四边形的判定和性质,根据平行四边形的性质得到,,根据角平分线的性质,结合平行线的性质,得到,进而得到,结合,即可得证.
【详解】证明:∵四边形是平行四边形,
∴,.
∵平分,平分,
∴,,
∴.
∵,
∴.
∴.
∴.
又∵,即,
∴四边形是平行四边形.
20.证明见解析
【分析】只需要分别证明ENMC,NFMB,即可证明四边形MENF为平行四边形.
【详解】证明:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠MCB=∠CMD,
∵∠BNE=∠CMD,
∴∠BNE=∠MCB,
∴ENMC,
∴∠NFC=∠ENF,
∵∠BEN=∠NFC,
∴∠BEN=∠ENF,
∴NFMB,
∴四边形MENF为平行四边形.
【点睛】本题主要考查了平行四边形的性质与判定,熟知平行四边形的性质与判定条件是解题的关键.
21.65;60.
【分析】先求出多边形的内角和,然后再利用方程求得未知数的值.
【详解】解:由四边形的内角和为360°,
则有:150°+80°+2x°=360°,解得x=65
由五边形内角和为:180°×(5-2)=540°,
则有:3x°+160°+90°+110°=540°,解得x=60
故答案为:65,60.
【点睛】本题考查了运用多边形内角和定理求多边形的内角的大小,解题关键在于求得多边形内角和,即多边形内角和=180°×(n-2)(n为多边形的边数).
22.(1)105°
(2)β-α=90°
(3)BE∥DF,理由见解析
【分析】(1)利用四边形的内角和和平角的定义推导即可;
(2)利用角平分线的定义,四边形的内角和以及三角形的内角和转化即可;
(3)利用角平分线的定义以及平行线的判定与性质即可解答.
【详解】(1)解:∵四边形ABCD的内角和为360°,
∴α+β=∠A+∠BCD=360°-(∠ABC+∠ADC),
∵∠MBC和∠NDC是四边形ABCD的外角,
∴∠MBC=180°-∠ABC,∠NDC=180°-∠ADC,
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC
=360°-(∠ABC+∠ADC),
=α+β
=105°;
(2)解:β-α=90°(或α-β=-90°等均正确).
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG= ∠MBC,∠CDG= ∠NDC,
∴∠CBG+∠CDG= ∠MBC+ ∠NDC= (∠MBC+∠NDC)= (α+β),
在△BCD中,∠BDC+∠CBD=180°-∠BCD=180°-β,
在△BDG中,∠BGD=45°,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(α+β)+180°-β+45°=180°,
∴β-α=90°.
故答案为β-α=90°(或α-β=-90°等均正确);
(3)解:BE∥DF.
理由:如图2,过点C作CP∥BE,
则∠EBC=∠BCP,
∴∠DCP=∠BCD-∠BCP=β-∠EBC,
由(1)知∠MBC+∠NDC=α+β,
∵α=β,
∴∠MBC+∠NDC=2β,
又∵BE、DF分别平分∠MBC和∠NDC,
∴∠EBC+∠FDC=(∠MBC+∠NDC)=β,
∴∠FDC=β-∠EBC,
又∵∠DCP=β-∠EBC,
∴∠FDC=∠DCP,
∴CP∥DF,
又CP∥BE,
∴BE∥DF.
【点睛】此题主要考查了平行线的性质及其判定、平角的定义,四边形的内角和,三角形内角和,角平分线的定义,用整体代换的思想是解本题的关键,整体思想是初中阶段的一种重要思想,要多加强训练.
23.详见解析
【分析】利用一组对边平行且相等得到四边形BDCE是平行四边形,然后利用对边平行得到两组角相等,进而整理到∠CDF=∠CMD,进而得证.
【详解】证明:∵四边形ABCD是平行四边形.
∴ABDC.
又∵BE=AB,
∴BEDC,
∴四边形BDCE是平行四边形.
∴DC∥BF,BD∥CE,
∴∠CDF=∠F,∠BDM=∠DMC.
∵BD=BF,
∴∠BDF=∠F.
∴∠CDF=∠CMD,
∴CD=CM.
【点睛】本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.当证明两条在一个三角形中的边相等时,通常是利用等角对等边来进行证明.
24.(1)见解析
(2)①;②
【分析】本题是四边形综合题,考查了平行四边形的性质,全等三角形的判定和性质,勾股定理,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.
(1)由可得,可得,可得结论;
(2)①由等腰三角形的性质可得由勾股定理可求,由等腰三角形的性质可求的长,即可求解;
②如图,过点H作于点M,证明,可得,由等腰直角三角形的性质可得,即可得结论.
【详解】(1)证明:∵平行四边形中,点O是对角线中点,
∴,
∴,且,
∴,
∴,且,
∴四边形是平行四边形;
(2)①如图2,过点D作点N,
∵,,
∴,
∴,
∵,
∴,
∴,
∴;
②,
理由如下:如图,过点H作于点M,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴
∴,且,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
