第七章一元一次不等式期末单元复习题(含解析)
文档属性
| 名称 | 第七章一元一次不等式期末单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 785.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 14:39:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第七章一元一次不等式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.不等式的解集为( )
A. B. C. D.
2.关于一元一次不等式, 下列说法正确的是( )
A.x可以是负数 B.x必须是正整数
C. x可以取 D.x可以取0
3.已知关于x的不等式的负整数解恰好是-3,-2,-1,则a的取值范围是( )
A. B. C. D.
4.下列说法不一定成立的是( )
A.若,则 B.若,则
C.若,则 D.若,则
5.下列解不等式的步骤中,错误的一步是( )
A.去分母,得 B.去括号,得
C.移项、合并同类项,得 D.系数化为1,得
6.已知、为非零常数,若的解集是,则的解集是( )
A.x>-3 B.x<-3 C.x>3 D.x<3
7.如果不等式的解集为,则a必须满足的条件是( )
A. B. C. D.
8.若,且,则的值可能是( )
A. B.0 C.1 D.4
9.若整数使关于的方程的解为负数,且使关于的不等式组无解,则所有满足条件的整数的值之和是( )
A.6 B.7 C.9 D.10
10.某品牌台灯的生产成本为220元,春节期间,商店为了让利给顾客,要求原价满300元的产品,需在原价的基础上减去50元出售,该品牌台灯为了保证利润率不低于,以下定价不能达到品牌要求的是( )
A.290元 B.330元 C.340元 D.350元
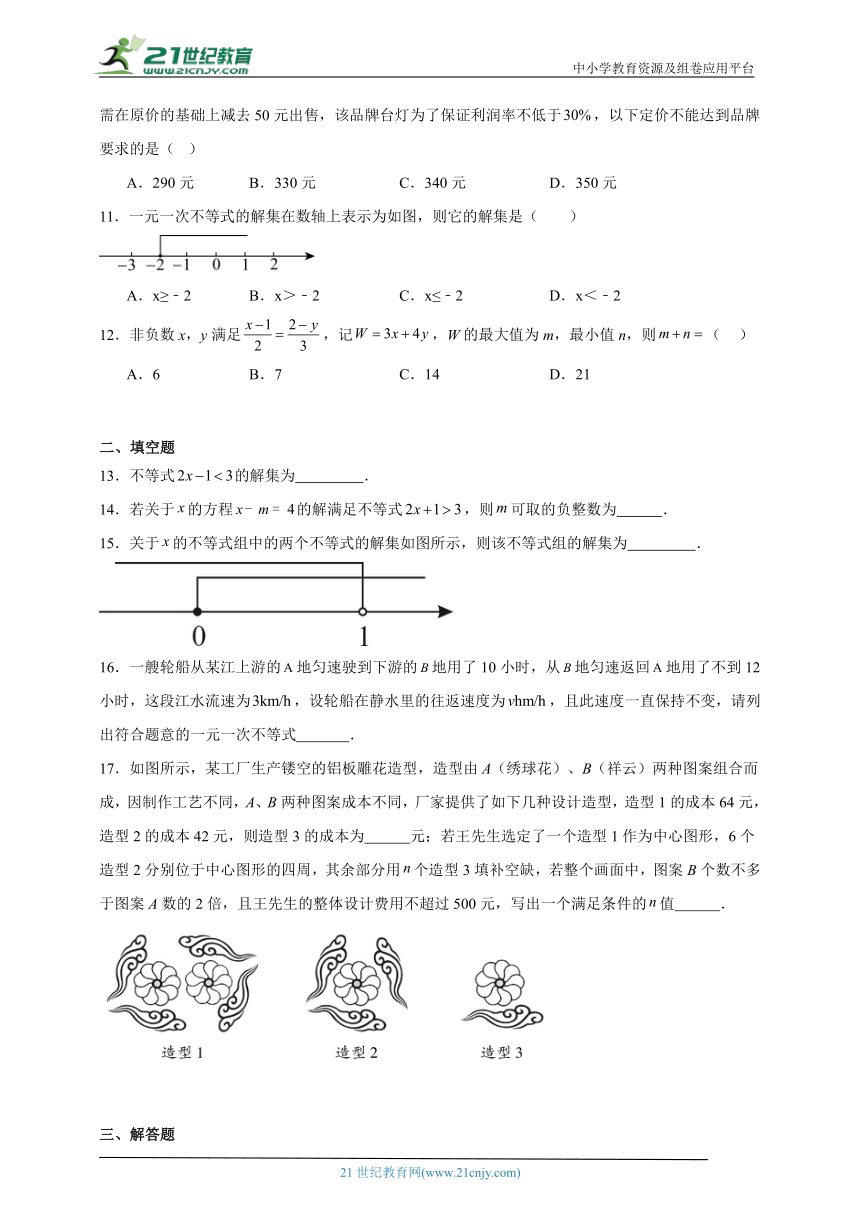
11.一元一次不等式的解集在数轴上表示为如图,则它的解集是( )
A.x≥﹣2 B.x>﹣2 C.x≤﹣2 D.x<﹣2
12.非负数x,y满足,记,W的最大值为m,最小值n,则( )
A.6 B.7 C.14 D.21
二、填空题
13.不等式的解集为 .
14.若关于的方程的解满足不等式,则可取的负整数为 .
15.关于的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为 .
16.一艘轮船从某江上游的地匀速驶到下游的地用了10小时,从地匀速返回地用了不到12小时,这段江水流速为,设轮船在静水里的往返速度为,且此速度一直保持不变,请列出符合题意的一元一次不等式 .
17.如图所示,某工厂生产镂空的铝板雕花造型,造型由A(绣球花)、B(祥云)两种图案组合而成,因制作工艺不同,A、B两种图案成本不同,厂家提供了如下几种设计造型,造型1的成本64元,造型2的成本42元,则造型3的成本为 元;若王先生选定了一个造型1作为中心图形,6个造型2分别位于中心图形的四周,其余部分用个造型3填补空缺,若整个画面中,图案B个数不多于图案A数的2倍,且王先生的整体设计费用不超过500元,写出一个满足条件的值 .
三、解答题
18.解不等式组:.
19.某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,有哪几种购买方案?
20.将下列不等式化成或的形式,并将解集在数轴上表示出来:
(1);
(2);
(3).
21.解下列不等式:
(1);
(2).
22.下面是小明同学解不等式组的过程,请认真阅读,完成相应的任务.
解:由不等式①,得.…第一步
解得.…第二步
由不等式②,得.…第三步
移项,得.…第四步
解得.…第五步
所以原不等式组的解集是.…第六步
任务一:
(1)小明的解答过程中,第__________步开始出现错误,错误的原因是__________;
(2)第三步的依据是__________;
任务二:
(3)直接写出这个不等式组正确的解集是__________.
23.学校举行八年级段数学知识竞赛,设立了一、二、三等奖,计划共购买件奖品,其中二等奖奖品件数比一等奖奖品件数的倍还少件,已知购买一等奖奖品件,各种奖品的单价如表:
奖品 一等奖奖品 二等奖奖品 三等奖奖品
单价(元)
(1)学校购买二等奖奖品 件,三等奖奖品 件;(用含的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品的费用的倍,且三等奖奖品的件数不少于一等奖奖品件数的倍.问学校共有几种购买方案?如何购买这三种奖品,使总费用最少?并求出最少的总费用.
24.解不等式或不等式组
(1)解不等式,并求出它的正整数解.
(2)解不等式组:
《第七章一元一次不等式》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D C D A D A D B
题号 11 12
答案 A D
1.C
【分析】不等式移项求出解集即可;
【详解】解不等式 得: ,
故选C
【点睛】此题考查了解一元一次不等式,熟练掌握运算法则是解本题的关键
2.C
【分析】本题考查了求一元一次不等式的解集,注意计算的准确性即可.
【详解】解:解不等式得:
∴x不可以是负数,故A错误;
x不必是正整数,故B错误;
x可以取 ,故C正确;
x不可以取0,故D错误;
故选:C
3.D
【解析】略
4.C
【分析】本题考查了不等式的性质,理解并掌握不等式的基本性质是解题关键.不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.据此求解即可.牢记不等式的性质是解题的关键.利用不等式的基本性质即可判断出正误.
【详解】解:∵,∴,故A选项成立;
∵,∴,故B选项成立;
∵,
∴当时,,故C选项不一定成立;
∵,
∴,而,
∴,故D选项成立.
故选:C.
5.D
【分析】按照去分母、去括号、移项、合并同类项、系数化为1的步骤求解,然后与各选项比较即可.
【详解】
去分母,得
去括号,得
移项、合并同类项,得
系数化为1,得
故选D.
【点睛】本题考查了一元一次不等式的解法,熟练掌握解一元一次不等式的步骤是解答本题的关键.
6.A
【分析】根据的解集是,得出的等量关系,再将的等量关系代入,解出不等式即可.
【详解】解:∵的解集是,
又∵不等号发生了变化,
∴,
又∵,即,
∴,
将代入不等式,可得:,
解得:.
故选:A.
【点睛】本题考查了不等式的性质和解一元一次不等式,在解题时要注意移项要改变符号这一点.不等式的两边同时乘以或除以同一个负数不等号的方向改变.正确判断出a、b的取值范围及关系是解本题的关键.
7.D
【分析】根据不等式的性质:不等式的两边同时乘以或除以同一个负数,不等号的方向改变可得,再解即可.
【详解】解:不等式的解集为,
,
,
故选:D.
【点睛】本题考查了不等式的性质,熟知该性质是解题的关键.
8.A
【分析】本题主要考查了不等式的性质,根据题意可知不等式两边同时乘以a之后不等号改变,则.
【详解】,且,
,
∴的值可能是.
故选:A.
9.D
【分析】先求出方程的解和不等式的解,得出a的范围,再求出整数解,最后求出答案即可.
【详解】解:解方程x+2a=1得:x=12a,
∵方程的解为负数,
∴12a<0,
解得:a>0.5,
∵解不等式①得:x<a,
解不等式②得:x≥4,
又∵不等式组无解,
∴a≤4,
∴a的取值范围是0.5<a≤4,
∴整数和为1+2+3+4=10,
故选:D.
【点睛】本题考查了解一元一次不等式,解一元一次不等式组,不等式组的整数解,解一元一次方程等知识点,能求出a的范围是解此题的关键.
10.B
【分析】本题考查了一元一次不等式的应用,根据题意得出台灯的最低售价为元才能保证利润率不低于,逐一分析各项即可得出答案,掌握一元一次不等式的应用是解题的关键.
【详解】解:根据题意可得,设台灯的最低售价为元,
解得:,
A、,故选项不符合题意;
B、,故选项符合题意;
C、,故选项不符合题意;
D、,故选项不符合题意;
故选:B.
11.A
【分析】根据不等式组解集在数轴上的表示方法可知不等式的解集.
【详解】由数轴可得:x≥﹣2,
故选A.
【点睛】不等式的解集在数轴上表示出来的方法:“>”空心圆点向右画折线,“≥”实心圆点向右画折线,“<”空心圆点向左画折线,“≤”实心圆点向左画折线.
12.D
【分析】设,用t表示出x、y的值,再由x,y为非负数即可求出t的取值范围,把所求代数式用t的形式表示出来,根据t的取值范围即可求解.
【详解】解:设,
则x=2t+1,y=2-3t,
∵x≥0,y≥0,
∴2t+1≥0,2-3t≥0,
解得
∴
∵w=3x+4y,把x=2t+1,y=2-3t,代入得:w=-6t+11,
∴
解得,7≤w≤14,
∴w的最大值是14,最小值是7,
∴m+n=14+7=21.
故选:D.
【点睛】本题考查了一元一次不等式组的应用,通过设参数的方法求出W的取值范围是解答此题的关键.
13.
【分析】此题考查了求不等式的解集.按照移项、合并同类项、系数化为1的步骤解不等式即可.
【详解】解:,
移项得,,
合并同类项得到,,
系数化为1得,,
故答案为:.
14.,
【分析】先解方程,求得,再解不等式得,然后解不等式,得出的取值范围,进而求解即可.
【详解】解:解方程,得,
解不等式,得,
∵关于的方程的解满足不等式,
∴,解得,
所以满足条件的的负整数值为,.
故答案为:,.
【点睛】此题考查了一元一次不等式的整数解,一元一次方程的解,解一元一次不等式,方程的解即为能使方程左右两边相等的未知数的值.求出方程的解是解题的关键.
15.
【分析】不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来向右画;,向左画,数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“”,“”要用实心圆点表示;“”,“”要用空心圆点表示.
【详解】解:该不等式组的解集为
故答案为:
【点睛】本题考查了不等式组解集在数轴上的表示方法,数形结合是解题的关键.
16.10(v+3)<12(v-3)
【分析】根据顺水航行10小时的路程≤12小时逆水航行的路程即可列出不等式.
【详解】解:∵这段江水流速为,设轮船在静水里的往返速度为,且此速度一直保持不变,
∴船在顺水中的速度为(v+3),船在逆水中的速度为(v-3),
∵轮船从某江上游的地匀速驶到下游的地用了10小时,从地匀速返回地用了不到12小时,
∴可列方程10(v+3)<12(v-3),
故答案为:10(v+3)<12(v-3).
【点睛】本题考查了一元一次不等式,能根据题目中的条件找到不等关系是列不等式的关键.
17. 22 6(答案不唯一,6,7,8均可)
【分析】设A种图案成本每个x元,B种图案成本每个y元,根据造型1的成本64元,造型2的成本42元,列方程组,得出x、y的值,则由造型3的成本为元;再根据图案的个数不多于图案个数的2倍,且整体设计费用不超过500元,列不等式组,求得,然后由n为整数,得出n的值即可.
【详解】解:设A种图案成本每个x元,B种图案成本每个y元,根据题意,得
,解得:,
∴(元),
即造型3的成本为22元;
故答案为:22;
根据题意得:,
解得:,
∵n为整数,
∴,7,8,
故答案为:6(答案不唯一,6,7,8均可).
【点睛】本题考查二元一次方程组与一元一次不等式组的应用,理解题意,列出方程组与不等式组是解题的关键.
18..
【分析】分别求出每个不等式的解,然后求两个不等式的交集即可.
本题主要考查解不等式组,解答本题的关键是熟练掌握解不等式组的解题方法与步骤,此题难度不大.
【详解】解:原不等式组为
解不等式①,得.
解不等式②,得.
∴原不等式组的解集为.
19.(1)每个气排球的价格是50元,每个篮球的价格是80元
(2)购买方案三种:①购买排球29个,篮球21个,②购买排球28个,篮球22个,③购买排球27个,篮球23个
【分析】(1)设每个气排球的价格是元,每个篮球的价格是元.根据“购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.”列出方程组,即可求解;
(2)设购买气排球个,则购买篮球个,根据“总费用不超过3200元,且购买气排球的个数少于30个,”列出不等式组,即可求解.
【详解】(1)解:设每个气排球的价格是元,每个篮球的价格是元.
根据题意得:,
解得:
所以每个气排球的价格是50元,每个篮球的价格是80元.
(2)解:设购买气排球个,则购买篮球个.
根据题意得:,
解得,
又∵为正整数,
∴排球的个数可以为27,28,29,
∴购买方案三种:①购买排球29个,篮球21个,
②购买排球28个,篮球22个,
③购买排球27个,篮球23个.
【点睛】本题主要考查了二元一次方程组的应用,一元一次不等式组的应用,明确题意,准确得到数量关系是解题的关键.
20.(1),见解析
(2),见解析
(3),见解析
【详解】(1)解:
两边都减3,得,
在数轴上表示解集为:
(2)解:,
两边都除以3,得,
在数轴上表示解集为:
(3)解:,
两边都乘,得,
在数轴上表示解集为:
21.(1);
(2).
【分析】本题考查了解一元一次不等式,能正确根据不等式的性质进行变形是解此题的关键.
(1)去分母,移项,合并同类项,系数化成1即可.
(2)去分母,去括号,移项,合并同类项,系数化成1即可.
【详解】(1)解:
去分母,得,
移项、合并同类项,得,
系数化为1,得.
(2)解:
去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得.
22.(1)五;不等式两边同时除以负数时,不等号方向没有改变
(2)不等式的性质2
(3)
【分析】本题考查了解一元一次不等式组,熟练掌握一元一次不等式组的解法是解题的关键.
(1)由不等式的性质可知,第五步不等式两边同时除以一个负数时,不等号方向没有发生改变,据此可得答案;
(2)根据不等式的性质2即可得出答案;
(3)先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集即可.
【详解】解:(1)由解题过程可知,第五步开始出现错误,错误的原因是:不等式两边同时除以负数时,不等号方向没有改变,
故答案为:五;不等式两边同时除以负数时,不等号方向没有改变;
(2)由解题过程可知,第三步是不等式两边同时乘以2去分母,因而第三步的依据是不等式的性质2,
故答案为:不等式的性质2;
(3),
由不等式①,去括号,得:,
移项,得:,
合并同类项,得:,
系数化为,得:;
由不等式②,去分母,得:,
移项,得:,
合并同类项,得:,
系数化为,得:;
不等式组的解集为:,
故答案为:.
23.(1);
(2)共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元
【分析】(1)根据一等奖奖品件及二等奖奖品件数比一等奖奖品件数的倍还少件,可得二等奖奖品件,由计划共购买件奖品,可得三等奖奖品件;
(2)根据题意列出不等式组,解出的取值范围,由为正整数,可得或,即共有两种购买方案,设总运费为,得出,分别求出当和时的总运费,比较选出运费最少的,并求出此时每种奖品的件数即可.
【详解】(1)解:学校购买二等奖奖品件,三等奖奖品件;
故答案为:;.
(2)解:根据题意可得:,
解得,
∵为正整数,
∴或,
设总费用为,则,
当时,(元),
当时,(元).
∴共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元.
【点睛】本题考查了一元一次不等式的实际应用,根据题目中的数量关系和不等关系列出不等式组是解答本题的关键.
24.(1)解集为,正整数解为1、2、3、4.
(2)
【分析】(1)按照解一元一次不等式的一般步骤求出解集,然后根据范围写出正整数解即可;
(2)分别求出两个不等式,然后取公共解.
【详解】(1)解:两边同时乘以6得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得:,
即解不等式的解集为.
∴原不等式的正整数解为1、2、3、4.
(2)解:
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:.
【点睛】本题考查一元一次不等式与一元一次不等式组得解法,掌握解一元一次不等式的一般方法和求解集公共部分的方法时解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章一元一次不等式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.不等式的解集为( )
A. B. C. D.
2.关于一元一次不等式, 下列说法正确的是( )
A.x可以是负数 B.x必须是正整数
C. x可以取 D.x可以取0
3.已知关于x的不等式的负整数解恰好是-3,-2,-1,则a的取值范围是( )
A. B. C. D.
4.下列说法不一定成立的是( )
A.若,则 B.若,则
C.若,则 D.若,则
5.下列解不等式的步骤中,错误的一步是( )
A.去分母,得 B.去括号,得
C.移项、合并同类项,得 D.系数化为1,得
6.已知、为非零常数,若的解集是,则的解集是( )
A.x>-3 B.x<-3 C.x>3 D.x<3
7.如果不等式的解集为,则a必须满足的条件是( )
A. B. C. D.
8.若,且,则的值可能是( )
A. B.0 C.1 D.4
9.若整数使关于的方程的解为负数,且使关于的不等式组无解,则所有满足条件的整数的值之和是( )
A.6 B.7 C.9 D.10
10.某品牌台灯的生产成本为220元,春节期间,商店为了让利给顾客,要求原价满300元的产品,需在原价的基础上减去50元出售,该品牌台灯为了保证利润率不低于,以下定价不能达到品牌要求的是( )
A.290元 B.330元 C.340元 D.350元
11.一元一次不等式的解集在数轴上表示为如图,则它的解集是( )
A.x≥﹣2 B.x>﹣2 C.x≤﹣2 D.x<﹣2
12.非负数x,y满足,记,W的最大值为m,最小值n,则( )
A.6 B.7 C.14 D.21
二、填空题
13.不等式的解集为 .
14.若关于的方程的解满足不等式,则可取的负整数为 .
15.关于的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为 .
16.一艘轮船从某江上游的地匀速驶到下游的地用了10小时,从地匀速返回地用了不到12小时,这段江水流速为,设轮船在静水里的往返速度为,且此速度一直保持不变,请列出符合题意的一元一次不等式 .
17.如图所示,某工厂生产镂空的铝板雕花造型,造型由A(绣球花)、B(祥云)两种图案组合而成,因制作工艺不同,A、B两种图案成本不同,厂家提供了如下几种设计造型,造型1的成本64元,造型2的成本42元,则造型3的成本为 元;若王先生选定了一个造型1作为中心图形,6个造型2分别位于中心图形的四周,其余部分用个造型3填补空缺,若整个画面中,图案B个数不多于图案A数的2倍,且王先生的整体设计费用不超过500元,写出一个满足条件的值 .
三、解答题
18.解不等式组:.
19.某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,有哪几种购买方案?
20.将下列不等式化成或的形式,并将解集在数轴上表示出来:
(1);
(2);
(3).
21.解下列不等式:
(1);
(2).
22.下面是小明同学解不等式组的过程,请认真阅读,完成相应的任务.
解:由不等式①,得.…第一步
解得.…第二步
由不等式②,得.…第三步
移项,得.…第四步
解得.…第五步
所以原不等式组的解集是.…第六步
任务一:
(1)小明的解答过程中,第__________步开始出现错误,错误的原因是__________;
(2)第三步的依据是__________;
任务二:
(3)直接写出这个不等式组正确的解集是__________.
23.学校举行八年级段数学知识竞赛,设立了一、二、三等奖,计划共购买件奖品,其中二等奖奖品件数比一等奖奖品件数的倍还少件,已知购买一等奖奖品件,各种奖品的单价如表:
奖品 一等奖奖品 二等奖奖品 三等奖奖品
单价(元)
(1)学校购买二等奖奖品 件,三等奖奖品 件;(用含的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品的费用的倍,且三等奖奖品的件数不少于一等奖奖品件数的倍.问学校共有几种购买方案?如何购买这三种奖品,使总费用最少?并求出最少的总费用.
24.解不等式或不等式组
(1)解不等式,并求出它的正整数解.
(2)解不等式组:
《第七章一元一次不等式》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D C D A D A D B
题号 11 12
答案 A D
1.C
【分析】不等式移项求出解集即可;
【详解】解不等式 得: ,
故选C
【点睛】此题考查了解一元一次不等式,熟练掌握运算法则是解本题的关键
2.C
【分析】本题考查了求一元一次不等式的解集,注意计算的准确性即可.
【详解】解:解不等式得:
∴x不可以是负数,故A错误;
x不必是正整数,故B错误;
x可以取 ,故C正确;
x不可以取0,故D错误;
故选:C
3.D
【解析】略
4.C
【分析】本题考查了不等式的性质,理解并掌握不等式的基本性质是解题关键.不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.据此求解即可.牢记不等式的性质是解题的关键.利用不等式的基本性质即可判断出正误.
【详解】解:∵,∴,故A选项成立;
∵,∴,故B选项成立;
∵,
∴当时,,故C选项不一定成立;
∵,
∴,而,
∴,故D选项成立.
故选:C.
5.D
【分析】按照去分母、去括号、移项、合并同类项、系数化为1的步骤求解,然后与各选项比较即可.
【详解】
去分母,得
去括号,得
移项、合并同类项,得
系数化为1,得
故选D.
【点睛】本题考查了一元一次不等式的解法,熟练掌握解一元一次不等式的步骤是解答本题的关键.
6.A
【分析】根据的解集是,得出的等量关系,再将的等量关系代入,解出不等式即可.
【详解】解:∵的解集是,
又∵不等号发生了变化,
∴,
又∵,即,
∴,
将代入不等式,可得:,
解得:.
故选:A.
【点睛】本题考查了不等式的性质和解一元一次不等式,在解题时要注意移项要改变符号这一点.不等式的两边同时乘以或除以同一个负数不等号的方向改变.正确判断出a、b的取值范围及关系是解本题的关键.
7.D
【分析】根据不等式的性质:不等式的两边同时乘以或除以同一个负数,不等号的方向改变可得,再解即可.
【详解】解:不等式的解集为,
,
,
故选:D.
【点睛】本题考查了不等式的性质,熟知该性质是解题的关键.
8.A
【分析】本题主要考查了不等式的性质,根据题意可知不等式两边同时乘以a之后不等号改变,则.
【详解】,且,
,
∴的值可能是.
故选:A.
9.D
【分析】先求出方程的解和不等式的解,得出a的范围,再求出整数解,最后求出答案即可.
【详解】解:解方程x+2a=1得:x=12a,
∵方程的解为负数,
∴12a<0,
解得:a>0.5,
∵解不等式①得:x<a,
解不等式②得:x≥4,
又∵不等式组无解,
∴a≤4,
∴a的取值范围是0.5<a≤4,
∴整数和为1+2+3+4=10,
故选:D.
【点睛】本题考查了解一元一次不等式,解一元一次不等式组,不等式组的整数解,解一元一次方程等知识点,能求出a的范围是解此题的关键.
10.B
【分析】本题考查了一元一次不等式的应用,根据题意得出台灯的最低售价为元才能保证利润率不低于,逐一分析各项即可得出答案,掌握一元一次不等式的应用是解题的关键.
【详解】解:根据题意可得,设台灯的最低售价为元,
解得:,
A、,故选项不符合题意;
B、,故选项符合题意;
C、,故选项不符合题意;
D、,故选项不符合题意;
故选:B.
11.A
【分析】根据不等式组解集在数轴上的表示方法可知不等式的解集.
【详解】由数轴可得:x≥﹣2,
故选A.
【点睛】不等式的解集在数轴上表示出来的方法:“>”空心圆点向右画折线,“≥”实心圆点向右画折线,“<”空心圆点向左画折线,“≤”实心圆点向左画折线.
12.D
【分析】设,用t表示出x、y的值,再由x,y为非负数即可求出t的取值范围,把所求代数式用t的形式表示出来,根据t的取值范围即可求解.
【详解】解:设,
则x=2t+1,y=2-3t,
∵x≥0,y≥0,
∴2t+1≥0,2-3t≥0,
解得
∴
∵w=3x+4y,把x=2t+1,y=2-3t,代入得:w=-6t+11,
∴
解得,7≤w≤14,
∴w的最大值是14,最小值是7,
∴m+n=14+7=21.
故选:D.
【点睛】本题考查了一元一次不等式组的应用,通过设参数的方法求出W的取值范围是解答此题的关键.
13.
【分析】此题考查了求不等式的解集.按照移项、合并同类项、系数化为1的步骤解不等式即可.
【详解】解:,
移项得,,
合并同类项得到,,
系数化为1得,,
故答案为:.
14.,
【分析】先解方程,求得,再解不等式得,然后解不等式,得出的取值范围,进而求解即可.
【详解】解:解方程,得,
解不等式,得,
∵关于的方程的解满足不等式,
∴,解得,
所以满足条件的的负整数值为,.
故答案为:,.
【点睛】此题考查了一元一次不等式的整数解,一元一次方程的解,解一元一次不等式,方程的解即为能使方程左右两边相等的未知数的值.求出方程的解是解题的关键.
15.
【分析】不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来向右画;,向左画,数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“”,“”要用实心圆点表示;“”,“”要用空心圆点表示.
【详解】解:该不等式组的解集为
故答案为:
【点睛】本题考查了不等式组解集在数轴上的表示方法,数形结合是解题的关键.
16.10(v+3)<12(v-3)
【分析】根据顺水航行10小时的路程≤12小时逆水航行的路程即可列出不等式.
【详解】解:∵这段江水流速为,设轮船在静水里的往返速度为,且此速度一直保持不变,
∴船在顺水中的速度为(v+3),船在逆水中的速度为(v-3),
∵轮船从某江上游的地匀速驶到下游的地用了10小时,从地匀速返回地用了不到12小时,
∴可列方程10(v+3)<12(v-3),
故答案为:10(v+3)<12(v-3).
【点睛】本题考查了一元一次不等式,能根据题目中的条件找到不等关系是列不等式的关键.
17. 22 6(答案不唯一,6,7,8均可)
【分析】设A种图案成本每个x元,B种图案成本每个y元,根据造型1的成本64元,造型2的成本42元,列方程组,得出x、y的值,则由造型3的成本为元;再根据图案的个数不多于图案个数的2倍,且整体设计费用不超过500元,列不等式组,求得,然后由n为整数,得出n的值即可.
【详解】解:设A种图案成本每个x元,B种图案成本每个y元,根据题意,得
,解得:,
∴(元),
即造型3的成本为22元;
故答案为:22;
根据题意得:,
解得:,
∵n为整数,
∴,7,8,
故答案为:6(答案不唯一,6,7,8均可).
【点睛】本题考查二元一次方程组与一元一次不等式组的应用,理解题意,列出方程组与不等式组是解题的关键.
18..
【分析】分别求出每个不等式的解,然后求两个不等式的交集即可.
本题主要考查解不等式组,解答本题的关键是熟练掌握解不等式组的解题方法与步骤,此题难度不大.
【详解】解:原不等式组为
解不等式①,得.
解不等式②,得.
∴原不等式组的解集为.
19.(1)每个气排球的价格是50元,每个篮球的价格是80元
(2)购买方案三种:①购买排球29个,篮球21个,②购买排球28个,篮球22个,③购买排球27个,篮球23个
【分析】(1)设每个气排球的价格是元,每个篮球的价格是元.根据“购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.”列出方程组,即可求解;
(2)设购买气排球个,则购买篮球个,根据“总费用不超过3200元,且购买气排球的个数少于30个,”列出不等式组,即可求解.
【详解】(1)解:设每个气排球的价格是元,每个篮球的价格是元.
根据题意得:,
解得:
所以每个气排球的价格是50元,每个篮球的价格是80元.
(2)解:设购买气排球个,则购买篮球个.
根据题意得:,
解得,
又∵为正整数,
∴排球的个数可以为27,28,29,
∴购买方案三种:①购买排球29个,篮球21个,
②购买排球28个,篮球22个,
③购买排球27个,篮球23个.
【点睛】本题主要考查了二元一次方程组的应用,一元一次不等式组的应用,明确题意,准确得到数量关系是解题的关键.
20.(1),见解析
(2),见解析
(3),见解析
【详解】(1)解:
两边都减3,得,
在数轴上表示解集为:
(2)解:,
两边都除以3,得,
在数轴上表示解集为:
(3)解:,
两边都乘,得,
在数轴上表示解集为:
21.(1);
(2).
【分析】本题考查了解一元一次不等式,能正确根据不等式的性质进行变形是解此题的关键.
(1)去分母,移项,合并同类项,系数化成1即可.
(2)去分母,去括号,移项,合并同类项,系数化成1即可.
【详解】(1)解:
去分母,得,
移项、合并同类项,得,
系数化为1,得.
(2)解:
去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为1,得.
22.(1)五;不等式两边同时除以负数时,不等号方向没有改变
(2)不等式的性质2
(3)
【分析】本题考查了解一元一次不等式组,熟练掌握一元一次不等式组的解法是解题的关键.
(1)由不等式的性质可知,第五步不等式两边同时除以一个负数时,不等号方向没有发生改变,据此可得答案;
(2)根据不等式的性质2即可得出答案;
(3)先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集即可.
【详解】解:(1)由解题过程可知,第五步开始出现错误,错误的原因是:不等式两边同时除以负数时,不等号方向没有改变,
故答案为:五;不等式两边同时除以负数时,不等号方向没有改变;
(2)由解题过程可知,第三步是不等式两边同时乘以2去分母,因而第三步的依据是不等式的性质2,
故答案为:不等式的性质2;
(3),
由不等式①,去括号,得:,
移项,得:,
合并同类项,得:,
系数化为,得:;
由不等式②,去分母,得:,
移项,得:,
合并同类项,得:,
系数化为,得:;
不等式组的解集为:,
故答案为:.
23.(1);
(2)共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元
【分析】(1)根据一等奖奖品件及二等奖奖品件数比一等奖奖品件数的倍还少件,可得二等奖奖品件,由计划共购买件奖品,可得三等奖奖品件;
(2)根据题意列出不等式组,解出的取值范围,由为正整数,可得或,即共有两种购买方案,设总运费为,得出,分别求出当和时的总运费,比较选出运费最少的,并求出此时每种奖品的件数即可.
【详解】(1)解:学校购买二等奖奖品件,三等奖奖品件;
故答案为:;.
(2)解:根据题意可得:,
解得,
∵为正整数,
∴或,
设总费用为,则,
当时,(元),
当时,(元).
∴共有两种购买方案,且当购买一等奖件,二等奖件,三等奖件时,总费用最少为元.
【点睛】本题考查了一元一次不等式的实际应用,根据题目中的数量关系和不等关系列出不等式组是解答本题的关键.
24.(1)解集为,正整数解为1、2、3、4.
(2)
【分析】(1)按照解一元一次不等式的一般步骤求出解集,然后根据范围写出正整数解即可;
(2)分别求出两个不等式,然后取公共解.
【详解】(1)解:两边同时乘以6得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得:,
即解不等式的解集为.
∴原不等式的正整数解为1、2、3、4.
(2)解:
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:.
【点睛】本题考查一元一次不等式与一元一次不等式组得解法,掌握解一元一次不等式的一般方法和求解集公共部分的方法时解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
