第九章轴对称、平移与旋转期末单元复习题(含解析)
文档属性
| 名称 | 第九章轴对称、平移与旋转期末单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章轴对称、平移与旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形中,绕某个点旋转72度后能与自身重合的是( )
A. B.
C. D.
2.若和关于直线l 对称,的面积为8,则的面积为( )
A.2 B.4 C.8 D.16
3.如图所示,与关于直线成轴对称,则线段与直线的关系正确的是( )
A.直线被线段垂直平分 B.线段被直线垂直平分
C.直线经过线段中点,但不垂直 D.直线与线段垂直,但不经过线段中点
4.如图是由三个全等的菱形拼接成的图形,若平移其中一个菱形,与其他两个菱形重新拼接(无覆盖,有公共顶点),可以拼接成不全等的轴对称图形有( )
A.3种 B.4种 C.6种 D.8种
5.下列说法正确的是( )
A.三角形的一个外角等于两个内角的和
B.一个三角形至少有两个锐角
C.两条直线被第三条直线所截,同旁内角互补
D.面积相等的两个三角形全等
6.如图,,且,,则的度数是( )
A. B. C. D.
7.如图,哪一个选项中的右边图形与左边图形成轴对称( ).
A. B.
C. D.
8.如图是从一块边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,则这块垫片的周长为( )
A.182cm B.191cm C.209cm D.218cm
9.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2026,则n的值为( )
A.407 B.406 C.405 D.404
10.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.菱形 B.平行四边形 C.正五边形 D.等边三角形
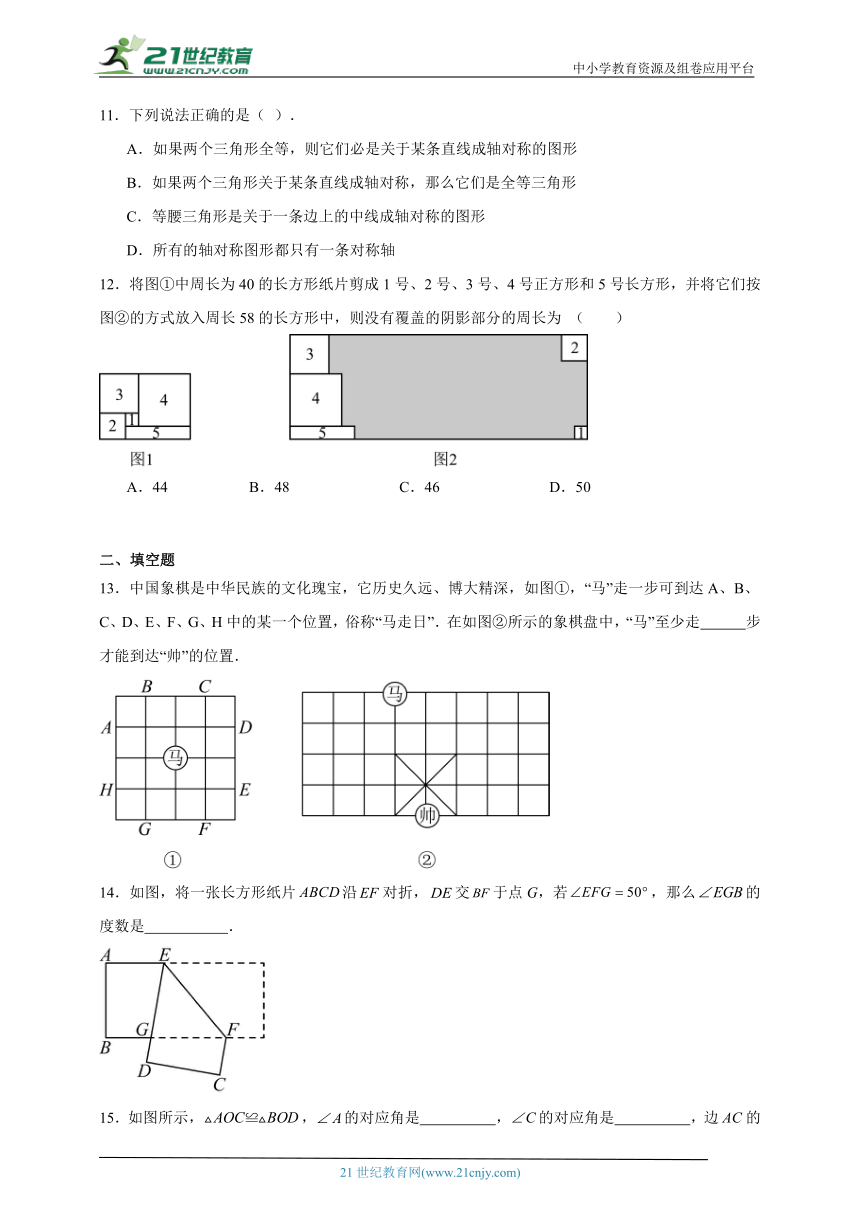
11.下列说法正确的是( ).
A.如果两个三角形全等,则它们必是关于某条直线成轴对称的图形
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于一条边上的中线成轴对称的图形
D.所有的轴对称图形都只有一条对称轴
12.将图①中周长为40的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图②的方式放入周长58的长方形中,则没有覆盖的阴影部分的周长为 ( )
A.44 B.48 C.46 D.50
二、填空题
13.中国象棋是中华民族的文化瑰宝,它历史久远、博大精深,如图①,“马”走一步可到达A、B、C、D、E、F、G、H中的某一个位置,俗称“马走日”.在如图②所示的象棋盘中,“马”至少走 步才能到达“帅”的位置.
14.如图,将一张长方形纸片沿对折,交于点G,若,那么的度数是 .
15.如图所示,,的对应角是 ,的对应角是 ,边的对应边是 .
16.如图,将沿方向平移得到,图中全等的三角形记为 ,其中点的对应点是 .
17.如图,将一张对边互相平行的纸条折叠.若,则的度数为 .
三、解答题
18.如图所示,直线与交于点,,试判断与的位置关系,并说明理由.
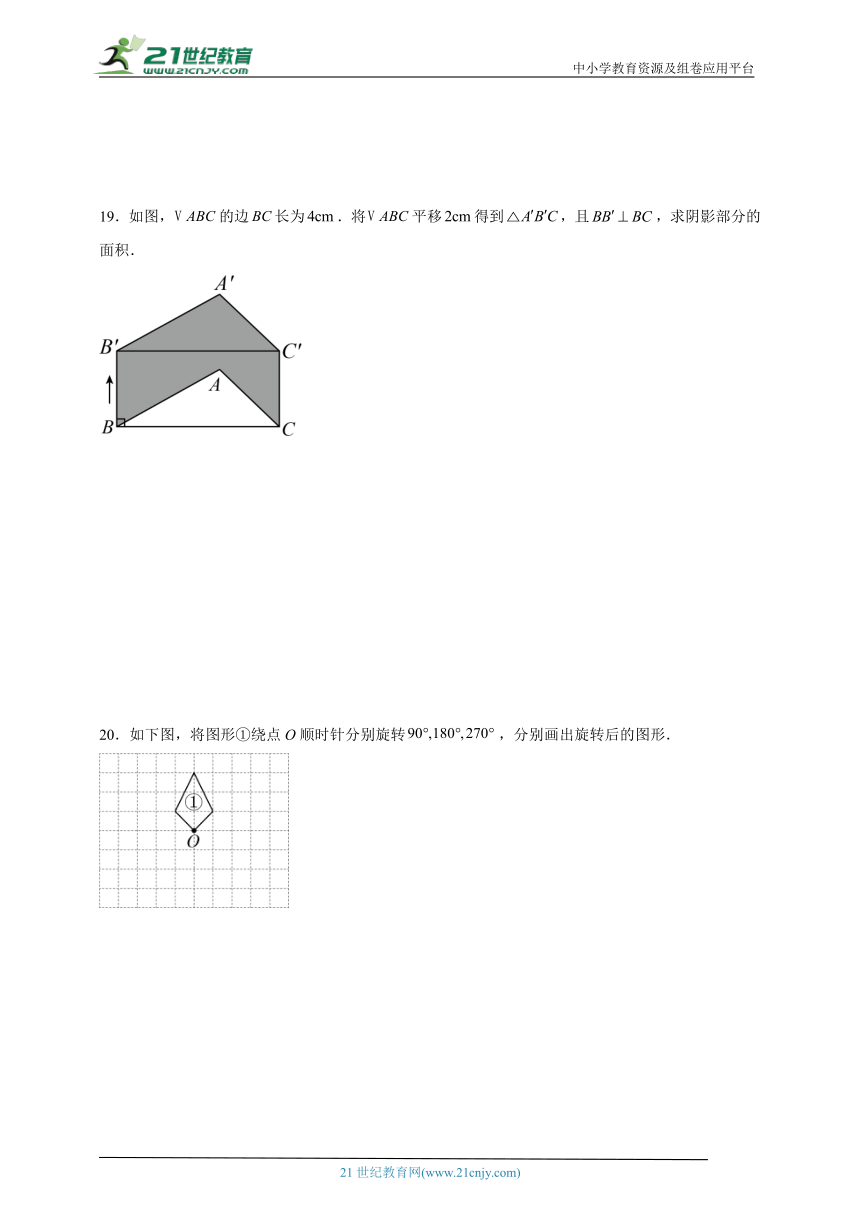
19.如图,的边长为.将平移得到,且,求阴影部分的面积.
20.如下图,将图形①绕点O顺时针分别旋转,分别画出旋转后的图形.
21.如图,直线,被直线所截,.
(1)作的平分线和的平分线;
(2)探究与的位置关系,并证明你的结论.
22.如图,为了做好交通安全工作,某交警执勤小队从点A处出发,先到公路上设卡检查,再到公路上设卡检查,最后到点B处执行任务,他们应如何走才能使总路程最短?
23.如图,在的网格中按要求画图并回答问题.
(1)画出关于直线对称的;
(2)画出关于点对称的;
(3)填空:与成轴对称吗?答:________(填写“成”或“不成”).如果成,请画出对称轴直线.
24.如图,已知中,,.将绕点A按逆时针方向旋转得到,与交于点F.
(1)若,求的度数;
(2)若平分,求的度数.
《第九章轴对称、平移与旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B B B B C D D A
题号 11 12
答案 B B
1.B
【分析】根据旋转的定义即可得出答案.
【详解】解:A.旋转90°后能与自身重合,不合题意;
B.旋转72°后能与自身重合,符合题意;
C.旋转60°后能与自身重合,不合题意;
D.旋转45°后能与自身重合,不合题意;
故选B.
【点睛】本题考查的是旋转:如果某一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形.
2.C
【分析】本题考查轴对称的性质,根据轴对称的性质可得即可得到答案.
【详解】∵和关于直线l 对称,
∴,
∴,
的面积为8,
∴的面积为8;
故选:C.
3.B
【分析】成轴对称图形的性质:对应点的连线被对称轴垂直平分,据此即可得到答案.
【详解】解:∵与关于直线成轴对称,
∴线段被直线垂直平分.
故选:B
【点睛】此题考查了成轴对称图形的性质,熟练掌握“成轴对称图形的对应点的连线被对称轴垂直平分”是解题的关键.
4.B
【分析】根据题意,画出图形,可得结论.
【详解】解;如图,共有四种可能.
故选:B.
【点睛】本题考查利用轴对称设计图案,解题的关键是理解题意,学会用图象法解决问题.
5.B
【分析】本题考查的是全等三角形的判定、三角形的外角性质、三角形内角和定理和平行线的性质,熟知以上知识是解答此题的关键.利用三角形的外角性质、三角形内角和定理和平行线的性质、全等三角形的判定分别判断后即可确定正确的选项.
【详解】解:A.三角形的一个外角等于和它不相邻的两个内角的和,原说法错误,不符合题意;
B.一个三角形中至少有两个锐角,原说法正确,符合题意;
C.两条平行线被第三条直线所截,同旁内角互补,原说法错误,不符合题意;
D.面积相等的两个三角形不一定全等,原说法错误,不符合题意;
故选:B.
6.B
【分析】本题主要考查了全等三角形的性质、三角形内角和定理等知识,熟练掌握全等三角形的性质是解题关键.
利用全等三角形的性质结合三角形内角和定理以及三角形外角的性质得出答案.
【详解】解:∵,
∴,
∵,,
∴,
∴,
∴.
故选:B.
7.C
【分析】本题考查了成轴对称图形的相关概念,掌握成轴对称图形的概念是解答本题的关键.根据成轴对称图形的相关概念逐项判断即可解答.
【详解】解:A、不符合成轴对称图形的相关概念,故A不符合题意;
B、不符合成轴对称图形的相关概念,故B不符合题意;
C、符合成轴对称图形的相关概念,故C符合题意;
D、不符合成轴对称图形的相关概念,故D不符合题意;
故选:C.
8.D
【分析】根据平移的思想进行求解即可.
【详解】解:在正方形中CD=BC=50cm,
由平移可知,
EF+GH+AB=CD=50cm,
AH+ED=BC+FG=50+9=59cm,
∴这块垫片的周长为50+50+59×2=218cm.
故选:D.
【点睛】本题考查了平移的实际问题,通过平移将垫片的周长与正方形的周长联系是解决问题的关键.
9.D
【分析】根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1-A1A2=6-5=1,进而求出AB1和AB2的长,由此得出ABn=5(n+1)×5+1,将2026代入求出n即可.
【详解】解:∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,
∴AA1=5,A1A2=5,A2B1=A1B1-A1A2=6-5=1,
∴AB1=AA1+A1A2+A2B1=5+5+1==2×5+1=11,
∴AB2的长为:5+5+6=3×5+1=16,
……
∴ABn=5(n+1)+1
5(n+1)+1=2026,
解得:n=404,
故选:D.
【点睛】此题主要考查了平移的性质以及一元一次方程的应用,根据平移的性质得出AA1=5,A1A2=5是解题关键.
10.A
【分析】本题主要考查了轴对称图形和中心对称图形,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
根据中心对称图形的定义和轴对称图形的定义进行逐项判断即可.
【详解】解:A、菱形是轴对称图形,是中心对称图形.故符合题意;
B、平行四边形不是轴对称图形,是中心对称图形.故不符合题意;
C、正五边形是轴对称图形,不是中心对称图形.故不符合题意;
D、等边三角形是轴对称图形,不是中心对称图形.故不符合题意.
故选:A.
11.B
【分析】根据全等三角形的定义以及轴对称的性质可判断选项A和B;根据等腰三角形的性质可判断选项C;根据对称轴的性质可判断选项D.
【详解】解:A、如果两个三角形全等,则它们不一定关于某条直线成轴对称,故本选项不合题意;
B、如果两个三角形关于某条直线成轴对称,那么它们是全等三角形,说法正确,故本选项符合题意;
C、等腰三角形是关于底边上的中线呈轴对称的图形,故本选项不合题意;
D、等边三角形就有三条对称轴,故本选项不合题意;
故选:B.
【点睛】本题考查了轴对称的性质,全等三角形的性质,等腰三角形的性质,关键是掌握性质进行逐一判断.
12.B
【分析】此题考查整式加减的应用,平移的性质,利用平移的性质将不规则图形变化为规则图形进而求解,解题的关键是设出未知数,列代数式表示各线段进而解决问题.
设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,根据图1中长方形的周长为40,求得,根据图中长方形的周长为58,求得,根据平移得:没有覆盖的阴影部分的周长为四边形的周长,计算即可得到答案.
【详解】解:设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,
由图1中长方形的周长为40,可得,,
解得:,
如图,∵图2中长方形的周长为58,
∴,
∴,
根据平移得:没有覆盖的阴影部分的周长为四边形的周长,
∴
;
故选:B.
13.3
【分析】结合“马走日”规则,分析“马”和“帅”之间相距的格数,并以此作为依据推出“马”行走的步数.
【详解】已知“马”和“帅”之间纵向相距个单位长度,横向相距个单位长度,结合图像进行以下假设:
①如果走步,“马”应落点黄色箭头所指的点,可直观看出无法走到“帅”处;
②如果走步,在①基础上,“马”应落点蓝色箭头所指的点,也无法步到达“帅”点;
③如果走步,在①②基础上,可有条线路能到达“帅”点,如下图绿色箭头所示.
故答案为:.
【点睛】本题考查的是对题意中“马走日”规则的理解,解题关键是结合图像进行假设.
14./度
【分析】本题主要考查了平行线的性质,折叠的性质,先由平行线的性质得到,,再由折叠的性质得到,由此即可得到答案.
【详解】解:∵,
∴,
由折叠的性质可得,
∴,
∴,
故答案为:.
15.
【分析】本题考查全等三角形的性质,根据图形确定对应边和对应角,进行作答即可.
【详解】解:∵,
∴的对应角是,的对应角是,边的对应边是边;
故答案为:,,.
16. 点
【分析】由平移的性质及全等三角形的性质即可得到答案.
【详解】解:将沿方向平移得到,
,
点的对应点是点,
故答案为:,点.
【点睛】本题主要考查了平移的性质、三角形全等的性质,熟练掌握平移的性质、三角形全等的性质是解题的关键.
17./55度
【分析】本题考查了平行线的性质,折叠的性质,掌握折叠的性质是解题的关键.由得,进而由平行线的性质得,又由折叠得,即得,据此即可求解.
【详解】解:如图,∵,
∴,
∵,
∴,
又由折叠得,,
∴,
故答案为:.
18.,理由见解析
【分析】本题主要考查了全等三角形的性质,平行线的判定,根据全等三角形对应角相等得到 ,从而利用平行线的判定定理可判断.
【详解】解:.理由如下:
,
,(全等三角形的对应角相等.)
.(内错角相等,两直线平行.)
19.
【分析】根据平移特点得出,得出阴影部分的面积长方形的面积.
【详解】解:∵将平移得到,
∴,
∵,
∴四边形是长方形,,
∴阴影部分的面积长方形的面积.
【点睛】本题主要考查了平移的性质,解题的关键是根据题意得出阴影部分的面积长方形的面积.
20.图见解析
【分析】本题考查旋转作图,根据旋转的性质,作图即可.
【详解】根据题意,画图如下:
②为旋转90度所得;③为旋转180度所得,④为旋转270度所得.
21.(1)作图见解析
(2),证明见解析
【分析】本题考查的是作角平分线,平行线的判定与性质;
(1)根据作角平分线的步骤画图即可;
(2)先证明,结合角平分线的定义可得,,可得,进一步可得结论.
【详解】(1)解:作的平分线和的平分线如下图:
(2)解:,理由如下:
∵,
∴.
∵分别平分和,
∴,,
∴,
∴.
22.见解析
【分析】利用轴对称的性质及两点之间线段最短即可求解.
【详解】解:如图所示,作点A关于直线的对称点,作点B关于直线的对称点,连接,分别交直线,于点C,D,连接,则C,D两点为所设卡检查点.
点A关于直线的对称点为,点B关于直线的对称点为,
,,
,
根据两点之间线段最短,可得沿走,才能时总路程最短.
【点睛】本题考查轴对称——最短路线问题,掌握轴对称的性质是解题的关键.
23.(1)见解析
(2)见解析
(3)成,见解析
【分析】本题考查了作图—轴对称变换、画中心对称图形、轴对称的性质,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)根据轴对称的性质画出图形即可;
(2)根据中心对称的性质画出图形即可;
(3)根据轴对称的性质解答即可.
【详解】(1)解:如图,即为所作,
(2)解:如图:即为所作;
(3)解:与成轴对称,对称轴为直线如图所示.
24.(1)
(2)
【分析】(1)由旋转的性质可得,即可求解;
(2)由三角形内角和定理可求的度数,由角平分线的性质和外角性质可求解.
本题主要考查了旋转的性质以及三角形内角和定理和外角定理,熟练掌握以上知识是解题的关键.
【详解】(1)证明:∵将绕点A按逆时针方向旋转得到,
,
,
,
;
(2)解:,,
,
平分,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章轴对称、平移与旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形中,绕某个点旋转72度后能与自身重合的是( )
A. B.
C. D.
2.若和关于直线l 对称,的面积为8,则的面积为( )
A.2 B.4 C.8 D.16
3.如图所示,与关于直线成轴对称,则线段与直线的关系正确的是( )
A.直线被线段垂直平分 B.线段被直线垂直平分
C.直线经过线段中点,但不垂直 D.直线与线段垂直,但不经过线段中点
4.如图是由三个全等的菱形拼接成的图形,若平移其中一个菱形,与其他两个菱形重新拼接(无覆盖,有公共顶点),可以拼接成不全等的轴对称图形有( )
A.3种 B.4种 C.6种 D.8种
5.下列说法正确的是( )
A.三角形的一个外角等于两个内角的和
B.一个三角形至少有两个锐角
C.两条直线被第三条直线所截,同旁内角互补
D.面积相等的两个三角形全等
6.如图,,且,,则的度数是( )
A. B. C. D.
7.如图,哪一个选项中的右边图形与左边图形成轴对称( ).
A. B.
C. D.
8.如图是从一块边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,则这块垫片的周长为( )
A.182cm B.191cm C.209cm D.218cm
9.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2026,则n的值为( )
A.407 B.406 C.405 D.404
10.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.菱形 B.平行四边形 C.正五边形 D.等边三角形
11.下列说法正确的是( ).
A.如果两个三角形全等,则它们必是关于某条直线成轴对称的图形
B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于一条边上的中线成轴对称的图形
D.所有的轴对称图形都只有一条对称轴
12.将图①中周长为40的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图②的方式放入周长58的长方形中,则没有覆盖的阴影部分的周长为 ( )
A.44 B.48 C.46 D.50
二、填空题
13.中国象棋是中华民族的文化瑰宝,它历史久远、博大精深,如图①,“马”走一步可到达A、B、C、D、E、F、G、H中的某一个位置,俗称“马走日”.在如图②所示的象棋盘中,“马”至少走 步才能到达“帅”的位置.
14.如图,将一张长方形纸片沿对折,交于点G,若,那么的度数是 .
15.如图所示,,的对应角是 ,的对应角是 ,边的对应边是 .
16.如图,将沿方向平移得到,图中全等的三角形记为 ,其中点的对应点是 .
17.如图,将一张对边互相平行的纸条折叠.若,则的度数为 .
三、解答题
18.如图所示,直线与交于点,,试判断与的位置关系,并说明理由.
19.如图,的边长为.将平移得到,且,求阴影部分的面积.
20.如下图,将图形①绕点O顺时针分别旋转,分别画出旋转后的图形.
21.如图,直线,被直线所截,.
(1)作的平分线和的平分线;
(2)探究与的位置关系,并证明你的结论.
22.如图,为了做好交通安全工作,某交警执勤小队从点A处出发,先到公路上设卡检查,再到公路上设卡检查,最后到点B处执行任务,他们应如何走才能使总路程最短?
23.如图,在的网格中按要求画图并回答问题.
(1)画出关于直线对称的;
(2)画出关于点对称的;
(3)填空:与成轴对称吗?答:________(填写“成”或“不成”).如果成,请画出对称轴直线.
24.如图,已知中,,.将绕点A按逆时针方向旋转得到,与交于点F.
(1)若,求的度数;
(2)若平分,求的度数.
《第九章轴对称、平移与旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B B B B C D D A
题号 11 12
答案 B B
1.B
【分析】根据旋转的定义即可得出答案.
【详解】解:A.旋转90°后能与自身重合,不合题意;
B.旋转72°后能与自身重合,符合题意;
C.旋转60°后能与自身重合,不合题意;
D.旋转45°后能与自身重合,不合题意;
故选B.
【点睛】本题考查的是旋转:如果某一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形.
2.C
【分析】本题考查轴对称的性质,根据轴对称的性质可得即可得到答案.
【详解】∵和关于直线l 对称,
∴,
∴,
的面积为8,
∴的面积为8;
故选:C.
3.B
【分析】成轴对称图形的性质:对应点的连线被对称轴垂直平分,据此即可得到答案.
【详解】解:∵与关于直线成轴对称,
∴线段被直线垂直平分.
故选:B
【点睛】此题考查了成轴对称图形的性质,熟练掌握“成轴对称图形的对应点的连线被对称轴垂直平分”是解题的关键.
4.B
【分析】根据题意,画出图形,可得结论.
【详解】解;如图,共有四种可能.
故选:B.
【点睛】本题考查利用轴对称设计图案,解题的关键是理解题意,学会用图象法解决问题.
5.B
【分析】本题考查的是全等三角形的判定、三角形的外角性质、三角形内角和定理和平行线的性质,熟知以上知识是解答此题的关键.利用三角形的外角性质、三角形内角和定理和平行线的性质、全等三角形的判定分别判断后即可确定正确的选项.
【详解】解:A.三角形的一个外角等于和它不相邻的两个内角的和,原说法错误,不符合题意;
B.一个三角形中至少有两个锐角,原说法正确,符合题意;
C.两条平行线被第三条直线所截,同旁内角互补,原说法错误,不符合题意;
D.面积相等的两个三角形不一定全等,原说法错误,不符合题意;
故选:B.
6.B
【分析】本题主要考查了全等三角形的性质、三角形内角和定理等知识,熟练掌握全等三角形的性质是解题关键.
利用全等三角形的性质结合三角形内角和定理以及三角形外角的性质得出答案.
【详解】解:∵,
∴,
∵,,
∴,
∴,
∴.
故选:B.
7.C
【分析】本题考查了成轴对称图形的相关概念,掌握成轴对称图形的概念是解答本题的关键.根据成轴对称图形的相关概念逐项判断即可解答.
【详解】解:A、不符合成轴对称图形的相关概念,故A不符合题意;
B、不符合成轴对称图形的相关概念,故B不符合题意;
C、符合成轴对称图形的相关概念,故C符合题意;
D、不符合成轴对称图形的相关概念,故D不符合题意;
故选:C.
8.D
【分析】根据平移的思想进行求解即可.
【详解】解:在正方形中CD=BC=50cm,
由平移可知,
EF+GH+AB=CD=50cm,
AH+ED=BC+FG=50+9=59cm,
∴这块垫片的周长为50+50+59×2=218cm.
故选:D.
【点睛】本题考查了平移的实际问题,通过平移将垫片的周长与正方形的周长联系是解决问题的关键.
9.D
【分析】根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1-A1A2=6-5=1,进而求出AB1和AB2的长,由此得出ABn=5(n+1)×5+1,将2026代入求出n即可.
【详解】解:∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,
∴AA1=5,A1A2=5,A2B1=A1B1-A1A2=6-5=1,
∴AB1=AA1+A1A2+A2B1=5+5+1==2×5+1=11,
∴AB2的长为:5+5+6=3×5+1=16,
……
∴ABn=5(n+1)+1
5(n+1)+1=2026,
解得:n=404,
故选:D.
【点睛】此题主要考查了平移的性质以及一元一次方程的应用,根据平移的性质得出AA1=5,A1A2=5是解题关键.
10.A
【分析】本题主要考查了轴对称图形和中心对称图形,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
根据中心对称图形的定义和轴对称图形的定义进行逐项判断即可.
【详解】解:A、菱形是轴对称图形,是中心对称图形.故符合题意;
B、平行四边形不是轴对称图形,是中心对称图形.故不符合题意;
C、正五边形是轴对称图形,不是中心对称图形.故不符合题意;
D、等边三角形是轴对称图形,不是中心对称图形.故不符合题意.
故选:A.
11.B
【分析】根据全等三角形的定义以及轴对称的性质可判断选项A和B;根据等腰三角形的性质可判断选项C;根据对称轴的性质可判断选项D.
【详解】解:A、如果两个三角形全等,则它们不一定关于某条直线成轴对称,故本选项不合题意;
B、如果两个三角形关于某条直线成轴对称,那么它们是全等三角形,说法正确,故本选项符合题意;
C、等腰三角形是关于底边上的中线呈轴对称的图形,故本选项不合题意;
D、等边三角形就有三条对称轴,故本选项不合题意;
故选:B.
【点睛】本题考查了轴对称的性质,全等三角形的性质,等腰三角形的性质,关键是掌握性质进行逐一判断.
12.B
【分析】此题考查整式加减的应用,平移的性质,利用平移的性质将不规则图形变化为规则图形进而求解,解题的关键是设出未知数,列代数式表示各线段进而解决问题.
设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,根据图1中长方形的周长为40,求得,根据图中长方形的周长为58,求得,根据平移得:没有覆盖的阴影部分的周长为四边形的周长,计算即可得到答案.
【详解】解:设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,
由图1中长方形的周长为40,可得,,
解得:,
如图,∵图2中长方形的周长为58,
∴,
∴,
根据平移得:没有覆盖的阴影部分的周长为四边形的周长,
∴
;
故选:B.
13.3
【分析】结合“马走日”规则,分析“马”和“帅”之间相距的格数,并以此作为依据推出“马”行走的步数.
【详解】已知“马”和“帅”之间纵向相距个单位长度,横向相距个单位长度,结合图像进行以下假设:
①如果走步,“马”应落点黄色箭头所指的点,可直观看出无法走到“帅”处;
②如果走步,在①基础上,“马”应落点蓝色箭头所指的点,也无法步到达“帅”点;
③如果走步,在①②基础上,可有条线路能到达“帅”点,如下图绿色箭头所示.
故答案为:.
【点睛】本题考查的是对题意中“马走日”规则的理解,解题关键是结合图像进行假设.
14./度
【分析】本题主要考查了平行线的性质,折叠的性质,先由平行线的性质得到,,再由折叠的性质得到,由此即可得到答案.
【详解】解:∵,
∴,
由折叠的性质可得,
∴,
∴,
故答案为:.
15.
【分析】本题考查全等三角形的性质,根据图形确定对应边和对应角,进行作答即可.
【详解】解:∵,
∴的对应角是,的对应角是,边的对应边是边;
故答案为:,,.
16. 点
【分析】由平移的性质及全等三角形的性质即可得到答案.
【详解】解:将沿方向平移得到,
,
点的对应点是点,
故答案为:,点.
【点睛】本题主要考查了平移的性质、三角形全等的性质,熟练掌握平移的性质、三角形全等的性质是解题的关键.
17./55度
【分析】本题考查了平行线的性质,折叠的性质,掌握折叠的性质是解题的关键.由得,进而由平行线的性质得,又由折叠得,即得,据此即可求解.
【详解】解:如图,∵,
∴,
∵,
∴,
又由折叠得,,
∴,
故答案为:.
18.,理由见解析
【分析】本题主要考查了全等三角形的性质,平行线的判定,根据全等三角形对应角相等得到 ,从而利用平行线的判定定理可判断.
【详解】解:.理由如下:
,
,(全等三角形的对应角相等.)
.(内错角相等,两直线平行.)
19.
【分析】根据平移特点得出,得出阴影部分的面积长方形的面积.
【详解】解:∵将平移得到,
∴,
∵,
∴四边形是长方形,,
∴阴影部分的面积长方形的面积.
【点睛】本题主要考查了平移的性质,解题的关键是根据题意得出阴影部分的面积长方形的面积.
20.图见解析
【分析】本题考查旋转作图,根据旋转的性质,作图即可.
【详解】根据题意,画图如下:
②为旋转90度所得;③为旋转180度所得,④为旋转270度所得.
21.(1)作图见解析
(2),证明见解析
【分析】本题考查的是作角平分线,平行线的判定与性质;
(1)根据作角平分线的步骤画图即可;
(2)先证明,结合角平分线的定义可得,,可得,进一步可得结论.
【详解】(1)解:作的平分线和的平分线如下图:
(2)解:,理由如下:
∵,
∴.
∵分别平分和,
∴,,
∴,
∴.
22.见解析
【分析】利用轴对称的性质及两点之间线段最短即可求解.
【详解】解:如图所示,作点A关于直线的对称点,作点B关于直线的对称点,连接,分别交直线,于点C,D,连接,则C,D两点为所设卡检查点.
点A关于直线的对称点为,点B关于直线的对称点为,
,,
,
根据两点之间线段最短,可得沿走,才能时总路程最短.
【点睛】本题考查轴对称——最短路线问题,掌握轴对称的性质是解题的关键.
23.(1)见解析
(2)见解析
(3)成,见解析
【分析】本题考查了作图—轴对称变换、画中心对称图形、轴对称的性质,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)根据轴对称的性质画出图形即可;
(2)根据中心对称的性质画出图形即可;
(3)根据轴对称的性质解答即可.
【详解】(1)解:如图,即为所作,
(2)解:如图:即为所作;
(3)解:与成轴对称,对称轴为直线如图所示.
24.(1)
(2)
【分析】(1)由旋转的性质可得,即可求解;
(2)由三角形内角和定理可求的度数,由角平分线的性质和外角性质可求解.
本题主要考查了旋转的性质以及三角形内角和定理和外角定理,熟练掌握以上知识是解题的关键.
【详解】(1)证明:∵将绕点A按逆时针方向旋转得到,
,
,
,
;
(2)解:,,
,
平分,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
