(期末培优卷)期末全真模拟押题卷-2024-2025学年四年级下学期数学青岛版(五四制)(含解析)
文档属性
| 名称 | (期末培优卷)期末全真模拟押题卷-2024-2025学年四年级下学期数学青岛版(五四制)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 293.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 19:56:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年四年级下学期数学期末全真模拟押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.对于下面三种图形面积,说法正确的是( )。
A.平行四边形面积最大 B.三角形面积最大
C.梯形面积最大 D.一样大
2.下列说法正确的是( )。
A.一个分数的分子越大,这个分数的分数值越大。
B.所有的奇数都是质数,所有的偶数都是合数。
C.求方程5X+5=15的解时,把5X看作一个整体。
D.假分数都大于1。
3.四年级一班同学的平均数学成绩是90分,以这个为标准,小亮的成绩用正负数表示为+3,那么小亮的成绩为( )分。
A.3 B.87 C.90 D.93
4.在一个上底是15厘米,下底是25厘米,高是12厘米的梯形纸片中,剪下一个最大的三角形,剩下的面积是( )平方厘米。
A.150 B.240 C.90 D.180
5.一块三角形标志牌的面积是30平方分米,底5分米,高是( )分米。
A.20 B.12 C.10
6.把长方形木框拉成一个平行四边形,它们的面积相比较,( )。
A.平行四边形面积大 B.长方形面积大 C.一样大 D.无法比较
7.要在一个上底8厘米,下底12厘米,高4厘米的梯形中剪一个最大的三角形,这个三角形的面积是( )。
A.40平方厘米 B.80平方厘米 C.24平方厘米 D.48平方厘米
8.下面涂色部分用分数表示是( )。
A. B. C.
二、填空题。(每空1分,共19分)
9.一个自然数比20小,它既是3的倍数,又有因数5,这个自然数是( )。
10.两个完全一样的三角形可以拼成一个( ),拼成图形的面积是原三角形面积的( )倍。
11.平行四边形的底是2.5米,高是1.2米,面积是( )平方米,和它等底等高的三角形面积是( )平方米。
12.一个四位数,个位上的数既是2的倍数又是3的倍数,十位上的数是最小的质数,百位上的数是合数但不是偶数,千位上的数既不是质数也不是合数,这个四位数是( )。
13.一个平行四边形的面积是15平方分米,从这个平行四边形中剪下一个最大的三角形,剩下的面积是( )平方分米。
14.某种药品的说明书标明保存温度是℃,由此可知该药品在( )℃至( )℃范围内保存才合适。
15.一个平行四边形比与它等底等高的三角形的面积多36平方厘米,这个三角形的面积是( )。
16.汽车的速度是90千米/时,自行车的速度是15千米/时,小明步行的速度是4千米/时,汽车的速度是自行车速( )倍;小明步行的速度是自行车的。
17.冬冬和姐姐年龄的乘积是165,已知他俩的年龄都小于20岁,则冬冬( )岁,姐姐( )岁。
18.把7个同样大小的面包平均分给4个同学,每个同学分得这些面包的,每个同学分得( )个面包。
19.一块长方形的布,长15分米,宽6分米。把它裁成正方形手绢(没有剩余),手绢的边长最长是( )分米,能裁( )块。
20.一个数,万位上是最小的质数,百位上是最小的奇数,十位上是最小的合数,其余数位上的数字是0,这个数写作( )。
三、判断题。(每题1分,共5分)
21.0、3、E、D、口、木都是近似轴对称图形。( )
22.两个非零的连续自然数的最小公倍数是它们的乘积。( )
23.的分子加上12,要使分数的大小不变,分母应该加上10。( )
24.统计宁阳6月的气温变化情况,用条形统计图比较合适。( )
25.非零自然数都能化成分母是1、2、3……的假分数。( )
四、计算题。(共26分)
26.直接写得数。(共10分)
200×90= 3.6÷4= 10÷0.5= 4.8×100= 3÷12=
27.脱式计算,能用简便方法的用简便方法。(共6分)
28.解方程。(共6分)
3.8x-x=0.56 17.4×3+4.8x=69
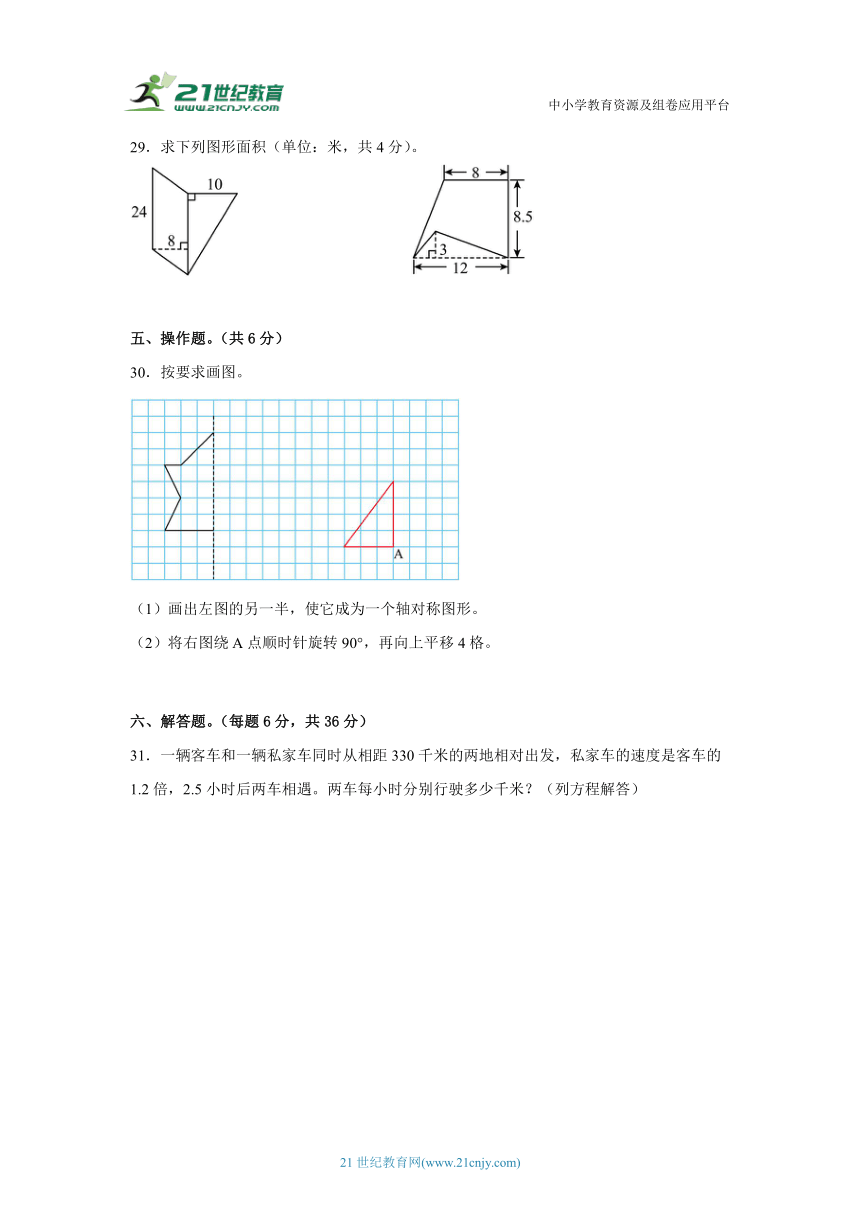
29.求下列图形面积(单位:米,共4分)。
五、操作题。(共6分)
30.按要求画图。
(1)画出左图的另一半,使它成为一个轴对称图形。
(2)将右图绕A点顺时针旋转90°,再向上平移4格。
六、解答题。(每题6分,共36分)
31.一辆客车和一辆私家车同时从相距330千米的两地相对出发,私家车的速度是客车的1.2倍,2.5小时后两车相遇。两车每小时分别行驶多少千米?(列方程解答)
32.跳绳是一项极佳的健体运动,能有效训练个人反应能力和耐力。阳光小学有短绳和长绳共120根,其中短绳是长绳根数的1.5倍,红旗小学短绳有多少根?(列方程解答)
33.根据相关研究,室内景点人均活动面积低于1平方米,室外景点人均活动面积低于0.75平方米时,就有发生踩踏事故的危险。在某古镇景点戏台前,有一个上底是32米、下底是48米、高是30米的梯形室外场地,为保证安全,这个场地最多能容纳多少人同时看戏?
34.快递员小李和小赵分别从相距240千米的东、西物流仓同时出发,驾驶货车相向而行调配物资,1.5小时后相遇。已知小李的货车比小赵每小时快16千米。求小赵驾驶的货车每小时行驶多少千米。
35.在社区环保活动中,小王比小李多收集了15公斤可回收物,小王收集的数量是小李的1.2倍,小王收集了多少公斤可回收物?(先写等量关系式再解答。)
等量关系式:______________________
列方程解答:
36.刘阿姨有一块底边长106米的平行四边形的梨园,为了种植的需要,刘阿姨又在梨园旁开出了一块底是12.5米,面积是175平方米的三角形地(如下图)。原来平行四边形的面积是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】根据题意,图中三个图形的高相同,根据梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,平行四边形的面积=底×高,分别求出它们的面积,再比较大小即可解答。
【解析】解:设这三个图形的高都是h。
梯形的面积:(1+4)×h÷2=5h÷2=2.5h(平方厘米)
三角形的面积:4×h÷2=2h(平方厘米)
平行四边形的面积:4×h=4h(平方厘米)
4h>2h>2.5h
三种图形面积,说法正确的是平行四边形面积最大。
故答案为:A
2.C
【分析】本题需要对每个选项所涉及的概念进行分析判断,依据分数值大小的决定因素、奇数与质数以及偶数与合数的定义、解方程的方法、假分数的定义来逐一判断选项的正确性。
【解析】A.分数值的大小不仅取决于分子,还与分母有关。当分母不变时,分子越大,分数值越大;但如果分母也发生变化,就不能仅根据分子大小判断分数值大小。所以A选项错误。
B.奇数是不能被2整除的整数,质数是除了1和它本身外没有其他因数的数;偶数是能被2整除的整数,合数是除了1和它本身外还有其他因数的数。9是奇数,但9=3×3,它不是质数;2是偶数,但它只有1和2两个因数,不是合数。所以B选项错误。
C.在求解方程5X+5=15时,我们可以把5X看作一个整体。根据等式的性质,等式两边同时减去5,然后再进一步求解X的值。所以C选项正确。
D.假分数是分子大于或者等于分母的分数,当分子等于分母时,假分数的值等于1,所以D选项错误。
故答案为:C
3.D
【分析】以平均成绩为标准,高于平均成绩记为正,低于平均成绩记为负,那么小亮成绩用正数表示的数值加上平均成绩就是小亮的实际成绩。
【解析】90+3=93分,所以小亮的成绩为93分。
故答案为:D
4.C
【分析】梯形面积公式为:(上底+下底)×高÷2。在梯形中剪最大的三角形时,应选择最长的底边(下底25厘米)作为三角形的底,顶点在另一底边的端点,此时高为梯形的高12厘米。剩余面积=梯形面积-最大三角形面积。
【解析】(15+25)×12÷2
=40×12÷2
=480÷2
=240(平方厘米)
25×12÷2
=300÷2
=150(平方厘米)
240-150=90(平方厘米)
在一个上底是15厘米,下底是25厘米,高是12厘米的梯形纸片中,剪下一个最大的三角形,剩下的面积是90平方厘米。
故答案为:C
5.B
【分析】根据题意,已知一块三角形标志牌的面积是30平方分米,底5分米,应用三角形的面积=底×高÷2,用30乘2,再除以5,就是三角形的高,列式计算即可。
【解析】根据分析可知:
30×2÷5
=60÷5
=12(分米)
一块三角形标志牌的面积是30平方分米,底5分米,高是12分米。
故答案为:B
6.B
【分析】
由图可知,把长方形木框拉成一个平行四边形,平行四边的底和长方形的长相等,平行四边形的高小于长方形的宽,平行四边形面积=底×高,长方形面积=长×宽,所以长方形面积大。
【解析】把长方形木框拉成一个平行四边形,它们的面积相比较,长方形面积大。
故答案为:B
7.C
【分析】在一个上底8厘米,下底12厘米,高4厘米的梯形中剪一个最大的三角形,这个最大的三角形的以这个梯形的下底为底,即为12厘米,高为这个梯形的高,即为4厘米,根据三角形的面积=底×高÷2,代入数据,即可求出这个三角形的面积是多少;据此解答。
【解析】12×4÷2
=48÷2
=24(平方厘米)
即要在一个上底8厘米,下底12厘米,高4厘米的梯形中剪一个最大的三角形,这个三角形的面积是24平方厘米。
故答案为:C
8.A
【分析】根据图中信息,第三个三角形平均分成3份,涂色部分占其中2份,前面有两个三角形被涂色,所以涂色部分表示的是,据此解答。
【解析】根据分析涂色部分用分数表示是。
故答案为:A
9.15
【分析】根据题意可知,这个自然数既是3的倍数,也是5的倍数;根据求一个数的倍数,就把这个数依次乘1、2、3……,分别找出20以内3的倍数和5的倍数,即可解答。
【解析】20以内3的倍数有:3、6、9、12、15、18
20以内5的倍数有:5、10、15、20
20以内既是3的倍数又是5的倍数的是:15
所以,一个自然数比20小,它既是3的倍数,又有因数5,这个自然数是15。
10.平行四边形 2
【分析】根据题意作图如下:
由图可知,两个完全一样的三角形可以拼成一个平行四边形。平行四边形的面积等于两个三角形的面积,所以拼成图形的面积是原三角形面积的2倍。
【解析】两个完全一样的三角形可以拼成一个平行四边形,拼成图形的面积是原三角形面积的2倍。
11.3 1.5
【分析】平行四边形的面积=底×高,所以用2.5×1.2即可计算出平行四边形的面积;三角形与此平行四边形等底等高,三角形面积=底×高÷2,据此用2.5×1.2÷2即可。
【解析】2.5×1.2=3(平方米)
2.5×1.2÷2
=3÷2
=1.5(平方米)
平行四边形的底是2.5米,高是1.2米,面积是3平方米,和它等底等高的三角形面积是1.5平方米。
12.1926
【分析】根据题意,个位上的数既是2的倍数又是3的倍数,即能被6整除,符合的数为6;最小的质数是2,所以十位上的数是2;既是奇数又是合数的数字是9,所以百位上是9;既不是质数也不是合数的数是1,所以千位上是1;所以这个数是1926。以此答题即可。
【解析】根据分析可知:
一个四位数,个位上的数既是2的倍数又是3的倍数,十位上的数是最小的质数,百位上的数是合数但不是偶数,千位上的数既不是质数也不是合数,这个四位数是1926。
13.7.5
【分析】从平行四边形中剪下一个最大的三角形,这个最大的三角形是与平行四边形等底等高的;根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知,从平行四边形中剪下一个最大的三角形的面积等于平行四边形的面积的一半,剪去最大三角形后剩下的面积也是平行四边形的一半;已知这个平行四边形的面积是15平方分米,则用15除以2,即可求出从平行四边形中剪下一个最大的三角形的面积,也就是剪去最大三角形后剩下的面积。
【解析】15÷2=7.5(平方米)
即一个平行四边形的面积是15平方分米,从这个平行四边形中剪下一个最大的三角形,剩下的面积是7.5平方分米。
14.17 23
【分析】根据题意,目中标明的保存温度为 (20±3)℃ ,表示温度以 20℃为基准,允许上下波动 3℃。最低温度:20-3=17℃最高温度:20+3=23℃,以此答题即可。
【解析】根据分析可知:
20-3=17℃
20+3=23℃
某种药品的说明书标明保存温度是 ( 20 ± 3 ) ℃,由此可知该药品在17℃至23℃范围内保存才合适。
15.36平方厘米/36cm2
【分析】平行四边形面积=底×高,三角形的面积=底×高÷2,如果平行四边形与三角形等底等高,则三角形面积是平行四边形面积的一半,所以一个平行四边形比与它等底等高的三角形的面积多36平方厘米即为三角形面积。
【解析】由分析可知:一个平行四边形比与它等底等高的三角形的面积多36平方厘米,这个三角形的面积是36平方厘米。
16.6;
【分析】求一个数是另一个数的几倍用除法,求一个数是另一个数的几分之几也用除法。求汽车速度是自行车速度的几倍:已知汽车速度是90千米/时,自行车速度是15千米/时,用汽车速度除以自行车速度可得汽车的速度是自行车速度的倍数;求小明步行速度是自行车速度的几分之几:已知小明步行速度是4千米/时,自行车速度是15千米/时,用小明步行速度除以自行车速度可得小明步行的速度是自行车的几分之几。
【解析】90÷15=6,所以汽车的速度是自行车速度的6倍。
4÷15=,所以小明步行的速度是自行车的。
17.11 15
【分析】先把165分解质因数,然后再改写成两个小于20的数的乘积,据此即可解答。
【解析】165=3×5×11=15×11
所以则冬冬11岁,姐姐15岁。
18.;
【分析】根据分数的初步认识,把7个同样大小的面包看作一个整体,平均分成4份,每份占这些面包的,即每个同学分得这些面包的;
分数与除数的关系:a÷b=(b≠0)。求每个同学分得多少个面包,用这些面包的总个数除以同学人数,即可解答。
【解析】由分析可得:把7个同样大小的面包平均分给4个同学,每个同学分得这些面包的。
7÷4=(个)
即把7个同样大小的面包平均分给4个同学,每个同学分得这些面包的,每个同学分得个面包。
19.3 10
【分析】根据题意,将长方形的布裁成大小相同的正方形且无剩余,正方形的边长必须是长和宽的公因数。边长最大是多少,即求15和6的最大公因数。
用长方形的长除以正方形手绢的最长边长就是长可以裁的块数。用长方形的宽除以正方形手绢的最长边长就是宽可以裁的块数。最后用长的块数乘宽的块数就是能裁的块数。以此答题即可。
【解析】15的因数:1、 3、 5、15, 6的因数:1、 2、 3、 6 。所以15和6的最大公因数为3。因此手绢的边长最长是3分米。
15÷3=5(块)
6÷3=2(块)
5×2=10(块)
所以,能裁10块。
20.20140
【分析】质数是指只能被1和它本身整除的数,合数是指除了1和它本身外,还有其它能整除的数;奇数是指不能被2整除的数。据此可得出答案。
【解析】万位是最小的质数,即为2;百位是最小的奇数,即为1;十位是最小的合数,即为4;其余数位上是0即千位和十位上是0。因此这个数是20140。
21.√
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。据此解答即可。
【解析】0、3、E、D、口、木都是近似轴对称图形,原题说法正确。
故答案为:√
22.√
【分析】根据题意,两个非0的连续自然数是互质的,互质的两个数的最小公倍数是这两个数的乘积。以此判断即可。
【解析】根据分析可知:
例如:两个连续的非零自然数3和4,5和6等,它们的最大公约数为1,它们的最小公倍数即为两数的乘积,3和4的最小公倍数是:3×4=12,5和6的最小公倍数是:5×6=30;所以两个非零的连续自然数的最小公倍数是它们的乘积。原题说法正确。
故答案为:√
23.×
【分析】分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。据此解答。
【解析】的分子加上12,4+12=16,那么分子就变为16。4×4=16,即分子乘4,要使分数的大小不变,分母也应该乘4。5×4=20,20-5=15,即分母应该加上15。原题说法错误。
故答案为:×
24.×
【分析】条形统计图能直观地看出数量的多少;折线统计图不仅能看出数量的多少,还能看出数量的增加变化情况。
【解析】统计宁阳6月的气温变化情况,用折线统计图比较合适。
故答案为:×
25.√
【分析】分子大于或等于分母的分数是假分数。整数可以化成假分数,分母可以是1、2、3、4……例如:2=……,
3=……
50=……
【解析】非零自然数都能化成分母是1、2、3……的假分数。
故答案为:√
26.1;;;;1
18000;0.9;20;480;
【解析】略
27.8;
10
【分析】先把写成小数0.6,然后观察,利用加法交换律和加法结合律进行简便运算即可;
观察发现的分子是17,的分子是7,17减去7刚好可以凑整,运用加法交换律交换和的位置,注意带着减号一起交换,然后再进行简便计算;
运用加法交换律,交换和0.77的位置后再运用加法结合律进行简便计算即可。
【解析】
=(0.64+6.36)+(0.6+0.4)
=7+1
=8
=--
=-
=
=(8.23+0.77)+(+)
=9+1
=10
28x=0.2;x=3.5;
【分析】(1)先计算3.8x-x=2.8x,再根据等式的性质2,等式两边同时除以2.8,据此解方程。
(2)先计算17.4×3=52.2,根据等式的性质1,等式两边同时减去52.2,再根据等式的性质2,等式两边同时除以4.8,据此解方程。
(3)根据等式的性质1,等式两边同时加上,据此解方程。
【解析】3.8x-x=0.56
解:2.8 x=0.56
2.8 x÷2.8=0.56÷2.8
x=0.2
17.4×3+4.8x=69
解:52.2+4.8x=69
52.2+4.8x-52.2=69-52.2
4.8x=16.8
4.8x÷4.8=16.8÷4.8
x=3.5
解:
x=
x=
29.312平方米;67平方米
【分析】(1)左边的图形由一个底是24米、高是4米的平行四边形,和一个底是24米、高是10米的直角三角形组成,根据平行四边形的面积=底×高,三角形面积=底×高÷2,据此代入数字计算出平行四边形和三角形的面积,相加即可求出这个图形的面积;
(2)右面的图形比一个上底是8米、下底是12米、高是8.5米的梯形,缺少一个底是12米、高是3米的三角形,根据梯形面积=(上底+下底)×高÷2,据此代入数字计算出梯形和三角形的面积后,用梯形的面积减去三角形的面积,即可求出该图形的面积;据此解答。
【解析】(1)(24×8)+(24×10÷2)
=192+120
=312(平方米)
所以左边图形的面积是312平方米。
(2)(8+12)×8.5÷2-(12×3÷2)
=20×8.5÷2-18
=170÷2-18
=85-18
=67(平方米)
所以右边图形的面积是67平方米。
30.(1)(2)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出左半图的关键对称点,依次连接即可补全这个轴对称图形。
(2)三角形绕点A旋转,点A不动。三条边分别绕点A顺时针旋转90°即可得到图形。根据平移的特征,把旋转后的三角形的三个顶点分别向上平移4格。依次连接即可得到平移后的图形。
【解析】具体画法如下所示:
31.客车:60千米;
私家车:72千米;
【分析】(1)设未知数:设客车每小时行驶x千米。因为题目中明确私家车的速度是客车的1.2倍,所以私家车每小时行驶1.2x千米。
(2)列方程:两车是相对出发,根据路程=速度和×时间,客车和私家车速度和是(1.2x+x),行驶的时间是2.5小时,行驶的路程是330千米。可列出方程(1.2x+x)×2.5=330。解方程求客车速度,最后求私家车的速度。
【解析】解:设客车每小时行驶x千米,则私家车每小时行驶1.2x千米。
(1.2x+x)×2.5=330
2.2x×2.5=330
2.2x×2.5÷2.5=330÷2.5
2.2x=132
2.2x÷2.2=150÷2.2
x=60
60×1.2=72(千米)
答:客车每小时行驶60千米,私家车每小时行驶72千米。
32.72根
【分析】根据题意,已知阳光小学有短绳和长绳共120根,其中短绳是长绳根数的1.5倍,设长绳有x根,则短绳有1.5x根。根据题意,短绳和长绳共120根,列方程为:x+1.5x=120,先计算x+1.5x=2.5x,再应用等式的性质2,等式两边同时除以2.5,解方程,求出长绳的数量,用长绳的数量乘1.5,就是短绳的数量。以此答题即可。
【解析】根据分析可知:
解:设长绳有x根,则短绳有1.5x根。
x+1.5x=120
2.5x=120
2.5x÷2.5=120÷2.5
x=48
48×1.5=72(根)
答:红旗小学短绳有72根。
33.1600人
【分析】梯形的面积=(上底+下底)×高÷2。由题意得,梯形室外场地的上底是32米、下底是48米、高是30米,那么直接将数据代入即可算出梯形室外场地的面积。室外景点人均活动面积应该大于或等于0.75平方米,那么直接用前面的得数除以0.75即可算出这个场地最多能容纳多少人同时看戏。
【解析】(32+48)×30÷2
=80×30÷2
=2400÷2
=1200(平方米)
1200÷0.75=1600(人)
答:这个场地最多能容纳1600人同时看戏。
34.72千米
【分析】根据题意,可以设小赵驾驶的货车每小时行驶x千米,小李的货车比小赵每小时快16千米,则小李的货车每小时行驶(x+16)千米,将行驶的距离相加再乘相遇的时间,即为两个物流仓之间的距离,据此列方程后根据等式的性质1和性质2解方程即可。
【解析】解:设小赵驾驶的货车每小时行驶x千米。
(x+16+x)×1.5=240
(x+16+x)×1.5÷1.5=240÷1.5
x+16+x=160
2x+16=160
2x+16-16=160-16
2x=144
2x÷2=144÷2
x=72
答:小赵驾驶的货车每小时行驶72千米。
35.等量关系式:小王收集的数量-小李收集的数量=小王比小李多收集了15公斤;
90公斤
【分析】根据条件小王比小李多收集了15公斤可回收物可得等量关系式,这里小李收集的数量×1.2=小王收集的数量。
设小李收集了x公斤可回收物,则小王收集了1.2x公斤可回收物,根据等量关系式列方程为:1.2x-x=15,方程左边合并为0.2x=15,根据等式的性质2左右两边同时除以0.2求得小李收集的数量,把方程的解代入1.2x中求出小王收集了多少公斤可回收物。
【解析】等量关系式是:小王收集的数量-小李收集的数量=小王比小李多收集了15公斤
解:设小李收集了x公斤可回收物,则小王收集了1.2x公斤可回收物。
1.2x-x=15
0.2x=15
0.2x÷0.2=15÷0.2
x=75
1.2x=1.2×75=90
答:小王收集了90公斤可回收物。
36.2968平方米
【分析】由题意得,三角形地的底是12.5米,面积是175平方米。三角形的高=面积×2÷底,直接将数据代入即可算出三角形的高,也就是原来平行四边形的高。平行四边形的面积=底×高,平行四边形梨园的底边长106米,直接将数据代入即可算出原来平行四边形的面积。
【解析】175×2÷12.5
=350÷12.5
=28(米)
106×28=2968(平方米)
答:原来平行四边形的面积是2968平方米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年四年级下学期数学期末全真模拟押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.对于下面三种图形面积,说法正确的是( )。
A.平行四边形面积最大 B.三角形面积最大
C.梯形面积最大 D.一样大
2.下列说法正确的是( )。
A.一个分数的分子越大,这个分数的分数值越大。
B.所有的奇数都是质数,所有的偶数都是合数。
C.求方程5X+5=15的解时,把5X看作一个整体。
D.假分数都大于1。
3.四年级一班同学的平均数学成绩是90分,以这个为标准,小亮的成绩用正负数表示为+3,那么小亮的成绩为( )分。
A.3 B.87 C.90 D.93
4.在一个上底是15厘米,下底是25厘米,高是12厘米的梯形纸片中,剪下一个最大的三角形,剩下的面积是( )平方厘米。
A.150 B.240 C.90 D.180
5.一块三角形标志牌的面积是30平方分米,底5分米,高是( )分米。
A.20 B.12 C.10
6.把长方形木框拉成一个平行四边形,它们的面积相比较,( )。
A.平行四边形面积大 B.长方形面积大 C.一样大 D.无法比较
7.要在一个上底8厘米,下底12厘米,高4厘米的梯形中剪一个最大的三角形,这个三角形的面积是( )。
A.40平方厘米 B.80平方厘米 C.24平方厘米 D.48平方厘米
8.下面涂色部分用分数表示是( )。
A. B. C.
二、填空题。(每空1分,共19分)
9.一个自然数比20小,它既是3的倍数,又有因数5,这个自然数是( )。
10.两个完全一样的三角形可以拼成一个( ),拼成图形的面积是原三角形面积的( )倍。
11.平行四边形的底是2.5米,高是1.2米,面积是( )平方米,和它等底等高的三角形面积是( )平方米。
12.一个四位数,个位上的数既是2的倍数又是3的倍数,十位上的数是最小的质数,百位上的数是合数但不是偶数,千位上的数既不是质数也不是合数,这个四位数是( )。
13.一个平行四边形的面积是15平方分米,从这个平行四边形中剪下一个最大的三角形,剩下的面积是( )平方分米。
14.某种药品的说明书标明保存温度是℃,由此可知该药品在( )℃至( )℃范围内保存才合适。
15.一个平行四边形比与它等底等高的三角形的面积多36平方厘米,这个三角形的面积是( )。
16.汽车的速度是90千米/时,自行车的速度是15千米/时,小明步行的速度是4千米/时,汽车的速度是自行车速( )倍;小明步行的速度是自行车的。
17.冬冬和姐姐年龄的乘积是165,已知他俩的年龄都小于20岁,则冬冬( )岁,姐姐( )岁。
18.把7个同样大小的面包平均分给4个同学,每个同学分得这些面包的,每个同学分得( )个面包。
19.一块长方形的布,长15分米,宽6分米。把它裁成正方形手绢(没有剩余),手绢的边长最长是( )分米,能裁( )块。
20.一个数,万位上是最小的质数,百位上是最小的奇数,十位上是最小的合数,其余数位上的数字是0,这个数写作( )。
三、判断题。(每题1分,共5分)
21.0、3、E、D、口、木都是近似轴对称图形。( )
22.两个非零的连续自然数的最小公倍数是它们的乘积。( )
23.的分子加上12,要使分数的大小不变,分母应该加上10。( )
24.统计宁阳6月的气温变化情况,用条形统计图比较合适。( )
25.非零自然数都能化成分母是1、2、3……的假分数。( )
四、计算题。(共26分)
26.直接写得数。(共10分)
200×90= 3.6÷4= 10÷0.5= 4.8×100= 3÷12=
27.脱式计算,能用简便方法的用简便方法。(共6分)
28.解方程。(共6分)
3.8x-x=0.56 17.4×3+4.8x=69
29.求下列图形面积(单位:米,共4分)。
五、操作题。(共6分)
30.按要求画图。
(1)画出左图的另一半,使它成为一个轴对称图形。
(2)将右图绕A点顺时针旋转90°,再向上平移4格。
六、解答题。(每题6分,共36分)
31.一辆客车和一辆私家车同时从相距330千米的两地相对出发,私家车的速度是客车的1.2倍,2.5小时后两车相遇。两车每小时分别行驶多少千米?(列方程解答)
32.跳绳是一项极佳的健体运动,能有效训练个人反应能力和耐力。阳光小学有短绳和长绳共120根,其中短绳是长绳根数的1.5倍,红旗小学短绳有多少根?(列方程解答)
33.根据相关研究,室内景点人均活动面积低于1平方米,室外景点人均活动面积低于0.75平方米时,就有发生踩踏事故的危险。在某古镇景点戏台前,有一个上底是32米、下底是48米、高是30米的梯形室外场地,为保证安全,这个场地最多能容纳多少人同时看戏?
34.快递员小李和小赵分别从相距240千米的东、西物流仓同时出发,驾驶货车相向而行调配物资,1.5小时后相遇。已知小李的货车比小赵每小时快16千米。求小赵驾驶的货车每小时行驶多少千米。
35.在社区环保活动中,小王比小李多收集了15公斤可回收物,小王收集的数量是小李的1.2倍,小王收集了多少公斤可回收物?(先写等量关系式再解答。)
等量关系式:______________________
列方程解答:
36.刘阿姨有一块底边长106米的平行四边形的梨园,为了种植的需要,刘阿姨又在梨园旁开出了一块底是12.5米,面积是175平方米的三角形地(如下图)。原来平行四边形的面积是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】根据题意,图中三个图形的高相同,根据梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,平行四边形的面积=底×高,分别求出它们的面积,再比较大小即可解答。
【解析】解:设这三个图形的高都是h。
梯形的面积:(1+4)×h÷2=5h÷2=2.5h(平方厘米)
三角形的面积:4×h÷2=2h(平方厘米)
平行四边形的面积:4×h=4h(平方厘米)
4h>2h>2.5h
三种图形面积,说法正确的是平行四边形面积最大。
故答案为:A
2.C
【分析】本题需要对每个选项所涉及的概念进行分析判断,依据分数值大小的决定因素、奇数与质数以及偶数与合数的定义、解方程的方法、假分数的定义来逐一判断选项的正确性。
【解析】A.分数值的大小不仅取决于分子,还与分母有关。当分母不变时,分子越大,分数值越大;但如果分母也发生变化,就不能仅根据分子大小判断分数值大小。所以A选项错误。
B.奇数是不能被2整除的整数,质数是除了1和它本身外没有其他因数的数;偶数是能被2整除的整数,合数是除了1和它本身外还有其他因数的数。9是奇数,但9=3×3,它不是质数;2是偶数,但它只有1和2两个因数,不是合数。所以B选项错误。
C.在求解方程5X+5=15时,我们可以把5X看作一个整体。根据等式的性质,等式两边同时减去5,然后再进一步求解X的值。所以C选项正确。
D.假分数是分子大于或者等于分母的分数,当分子等于分母时,假分数的值等于1,所以D选项错误。
故答案为:C
3.D
【分析】以平均成绩为标准,高于平均成绩记为正,低于平均成绩记为负,那么小亮成绩用正数表示的数值加上平均成绩就是小亮的实际成绩。
【解析】90+3=93分,所以小亮的成绩为93分。
故答案为:D
4.C
【分析】梯形面积公式为:(上底+下底)×高÷2。在梯形中剪最大的三角形时,应选择最长的底边(下底25厘米)作为三角形的底,顶点在另一底边的端点,此时高为梯形的高12厘米。剩余面积=梯形面积-最大三角形面积。
【解析】(15+25)×12÷2
=40×12÷2
=480÷2
=240(平方厘米)
25×12÷2
=300÷2
=150(平方厘米)
240-150=90(平方厘米)
在一个上底是15厘米,下底是25厘米,高是12厘米的梯形纸片中,剪下一个最大的三角形,剩下的面积是90平方厘米。
故答案为:C
5.B
【分析】根据题意,已知一块三角形标志牌的面积是30平方分米,底5分米,应用三角形的面积=底×高÷2,用30乘2,再除以5,就是三角形的高,列式计算即可。
【解析】根据分析可知:
30×2÷5
=60÷5
=12(分米)
一块三角形标志牌的面积是30平方分米,底5分米,高是12分米。
故答案为:B
6.B
【分析】
由图可知,把长方形木框拉成一个平行四边形,平行四边的底和长方形的长相等,平行四边形的高小于长方形的宽,平行四边形面积=底×高,长方形面积=长×宽,所以长方形面积大。
【解析】把长方形木框拉成一个平行四边形,它们的面积相比较,长方形面积大。
故答案为:B
7.C
【分析】在一个上底8厘米,下底12厘米,高4厘米的梯形中剪一个最大的三角形,这个最大的三角形的以这个梯形的下底为底,即为12厘米,高为这个梯形的高,即为4厘米,根据三角形的面积=底×高÷2,代入数据,即可求出这个三角形的面积是多少;据此解答。
【解析】12×4÷2
=48÷2
=24(平方厘米)
即要在一个上底8厘米,下底12厘米,高4厘米的梯形中剪一个最大的三角形,这个三角形的面积是24平方厘米。
故答案为:C
8.A
【分析】根据图中信息,第三个三角形平均分成3份,涂色部分占其中2份,前面有两个三角形被涂色,所以涂色部分表示的是,据此解答。
【解析】根据分析涂色部分用分数表示是。
故答案为:A
9.15
【分析】根据题意可知,这个自然数既是3的倍数,也是5的倍数;根据求一个数的倍数,就把这个数依次乘1、2、3……,分别找出20以内3的倍数和5的倍数,即可解答。
【解析】20以内3的倍数有:3、6、9、12、15、18
20以内5的倍数有:5、10、15、20
20以内既是3的倍数又是5的倍数的是:15
所以,一个自然数比20小,它既是3的倍数,又有因数5,这个自然数是15。
10.平行四边形 2
【分析】根据题意作图如下:
由图可知,两个完全一样的三角形可以拼成一个平行四边形。平行四边形的面积等于两个三角形的面积,所以拼成图形的面积是原三角形面积的2倍。
【解析】两个完全一样的三角形可以拼成一个平行四边形,拼成图形的面积是原三角形面积的2倍。
11.3 1.5
【分析】平行四边形的面积=底×高,所以用2.5×1.2即可计算出平行四边形的面积;三角形与此平行四边形等底等高,三角形面积=底×高÷2,据此用2.5×1.2÷2即可。
【解析】2.5×1.2=3(平方米)
2.5×1.2÷2
=3÷2
=1.5(平方米)
平行四边形的底是2.5米,高是1.2米,面积是3平方米,和它等底等高的三角形面积是1.5平方米。
12.1926
【分析】根据题意,个位上的数既是2的倍数又是3的倍数,即能被6整除,符合的数为6;最小的质数是2,所以十位上的数是2;既是奇数又是合数的数字是9,所以百位上是9;既不是质数也不是合数的数是1,所以千位上是1;所以这个数是1926。以此答题即可。
【解析】根据分析可知:
一个四位数,个位上的数既是2的倍数又是3的倍数,十位上的数是最小的质数,百位上的数是合数但不是偶数,千位上的数既不是质数也不是合数,这个四位数是1926。
13.7.5
【分析】从平行四边形中剪下一个最大的三角形,这个最大的三角形是与平行四边形等底等高的;根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知,从平行四边形中剪下一个最大的三角形的面积等于平行四边形的面积的一半,剪去最大三角形后剩下的面积也是平行四边形的一半;已知这个平行四边形的面积是15平方分米,则用15除以2,即可求出从平行四边形中剪下一个最大的三角形的面积,也就是剪去最大三角形后剩下的面积。
【解析】15÷2=7.5(平方米)
即一个平行四边形的面积是15平方分米,从这个平行四边形中剪下一个最大的三角形,剩下的面积是7.5平方分米。
14.17 23
【分析】根据题意,目中标明的保存温度为 (20±3)℃ ,表示温度以 20℃为基准,允许上下波动 3℃。最低温度:20-3=17℃最高温度:20+3=23℃,以此答题即可。
【解析】根据分析可知:
20-3=17℃
20+3=23℃
某种药品的说明书标明保存温度是 ( 20 ± 3 ) ℃,由此可知该药品在17℃至23℃范围内保存才合适。
15.36平方厘米/36cm2
【分析】平行四边形面积=底×高,三角形的面积=底×高÷2,如果平行四边形与三角形等底等高,则三角形面积是平行四边形面积的一半,所以一个平行四边形比与它等底等高的三角形的面积多36平方厘米即为三角形面积。
【解析】由分析可知:一个平行四边形比与它等底等高的三角形的面积多36平方厘米,这个三角形的面积是36平方厘米。
16.6;
【分析】求一个数是另一个数的几倍用除法,求一个数是另一个数的几分之几也用除法。求汽车速度是自行车速度的几倍:已知汽车速度是90千米/时,自行车速度是15千米/时,用汽车速度除以自行车速度可得汽车的速度是自行车速度的倍数;求小明步行速度是自行车速度的几分之几:已知小明步行速度是4千米/时,自行车速度是15千米/时,用小明步行速度除以自行车速度可得小明步行的速度是自行车的几分之几。
【解析】90÷15=6,所以汽车的速度是自行车速度的6倍。
4÷15=,所以小明步行的速度是自行车的。
17.11 15
【分析】先把165分解质因数,然后再改写成两个小于20的数的乘积,据此即可解答。
【解析】165=3×5×11=15×11
所以则冬冬11岁,姐姐15岁。
18.;
【分析】根据分数的初步认识,把7个同样大小的面包看作一个整体,平均分成4份,每份占这些面包的,即每个同学分得这些面包的;
分数与除数的关系:a÷b=(b≠0)。求每个同学分得多少个面包,用这些面包的总个数除以同学人数,即可解答。
【解析】由分析可得:把7个同样大小的面包平均分给4个同学,每个同学分得这些面包的。
7÷4=(个)
即把7个同样大小的面包平均分给4个同学,每个同学分得这些面包的,每个同学分得个面包。
19.3 10
【分析】根据题意,将长方形的布裁成大小相同的正方形且无剩余,正方形的边长必须是长和宽的公因数。边长最大是多少,即求15和6的最大公因数。
用长方形的长除以正方形手绢的最长边长就是长可以裁的块数。用长方形的宽除以正方形手绢的最长边长就是宽可以裁的块数。最后用长的块数乘宽的块数就是能裁的块数。以此答题即可。
【解析】15的因数:1、 3、 5、15, 6的因数:1、 2、 3、 6 。所以15和6的最大公因数为3。因此手绢的边长最长是3分米。
15÷3=5(块)
6÷3=2(块)
5×2=10(块)
所以,能裁10块。
20.20140
【分析】质数是指只能被1和它本身整除的数,合数是指除了1和它本身外,还有其它能整除的数;奇数是指不能被2整除的数。据此可得出答案。
【解析】万位是最小的质数,即为2;百位是最小的奇数,即为1;十位是最小的合数,即为4;其余数位上是0即千位和十位上是0。因此这个数是20140。
21.√
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。据此解答即可。
【解析】0、3、E、D、口、木都是近似轴对称图形,原题说法正确。
故答案为:√
22.√
【分析】根据题意,两个非0的连续自然数是互质的,互质的两个数的最小公倍数是这两个数的乘积。以此判断即可。
【解析】根据分析可知:
例如:两个连续的非零自然数3和4,5和6等,它们的最大公约数为1,它们的最小公倍数即为两数的乘积,3和4的最小公倍数是:3×4=12,5和6的最小公倍数是:5×6=30;所以两个非零的连续自然数的最小公倍数是它们的乘积。原题说法正确。
故答案为:√
23.×
【分析】分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。据此解答。
【解析】的分子加上12,4+12=16,那么分子就变为16。4×4=16,即分子乘4,要使分数的大小不变,分母也应该乘4。5×4=20,20-5=15,即分母应该加上15。原题说法错误。
故答案为:×
24.×
【分析】条形统计图能直观地看出数量的多少;折线统计图不仅能看出数量的多少,还能看出数量的增加变化情况。
【解析】统计宁阳6月的气温变化情况,用折线统计图比较合适。
故答案为:×
25.√
【分析】分子大于或等于分母的分数是假分数。整数可以化成假分数,分母可以是1、2、3、4……例如:2=……,
3=……
50=……
【解析】非零自然数都能化成分母是1、2、3……的假分数。
故答案为:√
26.1;;;;1
18000;0.9;20;480;
【解析】略
27.8;
10
【分析】先把写成小数0.6,然后观察,利用加法交换律和加法结合律进行简便运算即可;
观察发现的分子是17,的分子是7,17减去7刚好可以凑整,运用加法交换律交换和的位置,注意带着减号一起交换,然后再进行简便计算;
运用加法交换律,交换和0.77的位置后再运用加法结合律进行简便计算即可。
【解析】
=(0.64+6.36)+(0.6+0.4)
=7+1
=8
=--
=-
=
=(8.23+0.77)+(+)
=9+1
=10
28x=0.2;x=3.5;
【分析】(1)先计算3.8x-x=2.8x,再根据等式的性质2,等式两边同时除以2.8,据此解方程。
(2)先计算17.4×3=52.2,根据等式的性质1,等式两边同时减去52.2,再根据等式的性质2,等式两边同时除以4.8,据此解方程。
(3)根据等式的性质1,等式两边同时加上,据此解方程。
【解析】3.8x-x=0.56
解:2.8 x=0.56
2.8 x÷2.8=0.56÷2.8
x=0.2
17.4×3+4.8x=69
解:52.2+4.8x=69
52.2+4.8x-52.2=69-52.2
4.8x=16.8
4.8x÷4.8=16.8÷4.8
x=3.5
解:
x=
x=
29.312平方米;67平方米
【分析】(1)左边的图形由一个底是24米、高是4米的平行四边形,和一个底是24米、高是10米的直角三角形组成,根据平行四边形的面积=底×高,三角形面积=底×高÷2,据此代入数字计算出平行四边形和三角形的面积,相加即可求出这个图形的面积;
(2)右面的图形比一个上底是8米、下底是12米、高是8.5米的梯形,缺少一个底是12米、高是3米的三角形,根据梯形面积=(上底+下底)×高÷2,据此代入数字计算出梯形和三角形的面积后,用梯形的面积减去三角形的面积,即可求出该图形的面积;据此解答。
【解析】(1)(24×8)+(24×10÷2)
=192+120
=312(平方米)
所以左边图形的面积是312平方米。
(2)(8+12)×8.5÷2-(12×3÷2)
=20×8.5÷2-18
=170÷2-18
=85-18
=67(平方米)
所以右边图形的面积是67平方米。
30.(1)(2)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出左半图的关键对称点,依次连接即可补全这个轴对称图形。
(2)三角形绕点A旋转,点A不动。三条边分别绕点A顺时针旋转90°即可得到图形。根据平移的特征,把旋转后的三角形的三个顶点分别向上平移4格。依次连接即可得到平移后的图形。
【解析】具体画法如下所示:
31.客车:60千米;
私家车:72千米;
【分析】(1)设未知数:设客车每小时行驶x千米。因为题目中明确私家车的速度是客车的1.2倍,所以私家车每小时行驶1.2x千米。
(2)列方程:两车是相对出发,根据路程=速度和×时间,客车和私家车速度和是(1.2x+x),行驶的时间是2.5小时,行驶的路程是330千米。可列出方程(1.2x+x)×2.5=330。解方程求客车速度,最后求私家车的速度。
【解析】解:设客车每小时行驶x千米,则私家车每小时行驶1.2x千米。
(1.2x+x)×2.5=330
2.2x×2.5=330
2.2x×2.5÷2.5=330÷2.5
2.2x=132
2.2x÷2.2=150÷2.2
x=60
60×1.2=72(千米)
答:客车每小时行驶60千米,私家车每小时行驶72千米。
32.72根
【分析】根据题意,已知阳光小学有短绳和长绳共120根,其中短绳是长绳根数的1.5倍,设长绳有x根,则短绳有1.5x根。根据题意,短绳和长绳共120根,列方程为:x+1.5x=120,先计算x+1.5x=2.5x,再应用等式的性质2,等式两边同时除以2.5,解方程,求出长绳的数量,用长绳的数量乘1.5,就是短绳的数量。以此答题即可。
【解析】根据分析可知:
解:设长绳有x根,则短绳有1.5x根。
x+1.5x=120
2.5x=120
2.5x÷2.5=120÷2.5
x=48
48×1.5=72(根)
答:红旗小学短绳有72根。
33.1600人
【分析】梯形的面积=(上底+下底)×高÷2。由题意得,梯形室外场地的上底是32米、下底是48米、高是30米,那么直接将数据代入即可算出梯形室外场地的面积。室外景点人均活动面积应该大于或等于0.75平方米,那么直接用前面的得数除以0.75即可算出这个场地最多能容纳多少人同时看戏。
【解析】(32+48)×30÷2
=80×30÷2
=2400÷2
=1200(平方米)
1200÷0.75=1600(人)
答:这个场地最多能容纳1600人同时看戏。
34.72千米
【分析】根据题意,可以设小赵驾驶的货车每小时行驶x千米,小李的货车比小赵每小时快16千米,则小李的货车每小时行驶(x+16)千米,将行驶的距离相加再乘相遇的时间,即为两个物流仓之间的距离,据此列方程后根据等式的性质1和性质2解方程即可。
【解析】解:设小赵驾驶的货车每小时行驶x千米。
(x+16+x)×1.5=240
(x+16+x)×1.5÷1.5=240÷1.5
x+16+x=160
2x+16=160
2x+16-16=160-16
2x=144
2x÷2=144÷2
x=72
答:小赵驾驶的货车每小时行驶72千米。
35.等量关系式:小王收集的数量-小李收集的数量=小王比小李多收集了15公斤;
90公斤
【分析】根据条件小王比小李多收集了15公斤可回收物可得等量关系式,这里小李收集的数量×1.2=小王收集的数量。
设小李收集了x公斤可回收物,则小王收集了1.2x公斤可回收物,根据等量关系式列方程为:1.2x-x=15,方程左边合并为0.2x=15,根据等式的性质2左右两边同时除以0.2求得小李收集的数量,把方程的解代入1.2x中求出小王收集了多少公斤可回收物。
【解析】等量关系式是:小王收集的数量-小李收集的数量=小王比小李多收集了15公斤
解:设小李收集了x公斤可回收物,则小王收集了1.2x公斤可回收物。
1.2x-x=15
0.2x=15
0.2x÷0.2=15÷0.2
x=75
1.2x=1.2×75=90
答:小王收集了90公斤可回收物。
36.2968平方米
【分析】由题意得,三角形地的底是12.5米,面积是175平方米。三角形的高=面积×2÷底,直接将数据代入即可算出三角形的高,也就是原来平行四边形的高。平行四边形的面积=底×高,平行四边形梨园的底边长106米,直接将数据代入即可算出原来平行四边形的面积。
【解析】175×2÷12.5
=350÷12.5
=28(米)
106×28=2968(平方米)
答:原来平行四边形的面积是2968平方米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
