4.2角(第1课时) 教学课件(共24张PPT)初中数学北师大版(2024)七年级上册
文档属性
| 名称 | 4.2角(第1课时) 教学课件(共24张PPT)初中数学北师大版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 33.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 19:32:41 | ||
图片预览




文档简介
(共24张PPT)
4.2角
(第 1 课时)
第四章 基本平面图形
北师大版(2024)七年级上册
学习目标
理解角的概念,掌握角的表示方法
01
理解平角、周角的概念,掌握角的常用度量单位:度、分、秒,及它们之间的换算关系,并会进行简单的换算
02
知识引入
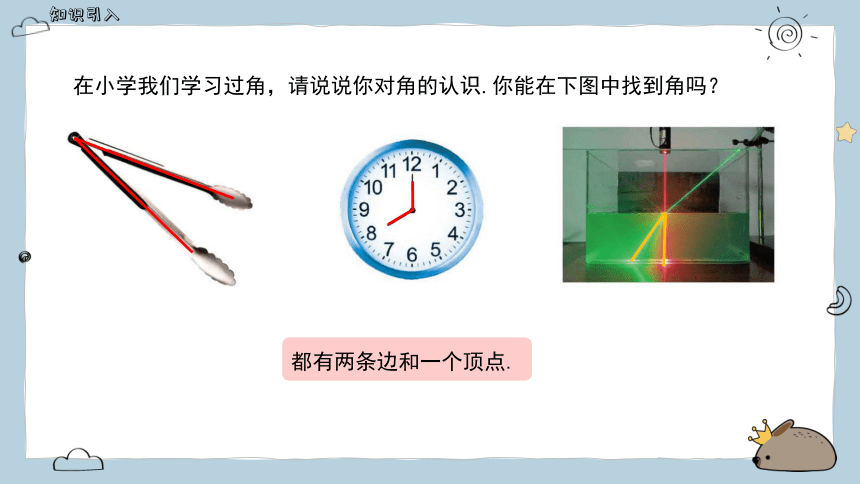
在小学我们学习过角,请说说你对角的认识. 你能在下图中找到角吗?
都有两条边和一个顶点.
知识探究
角
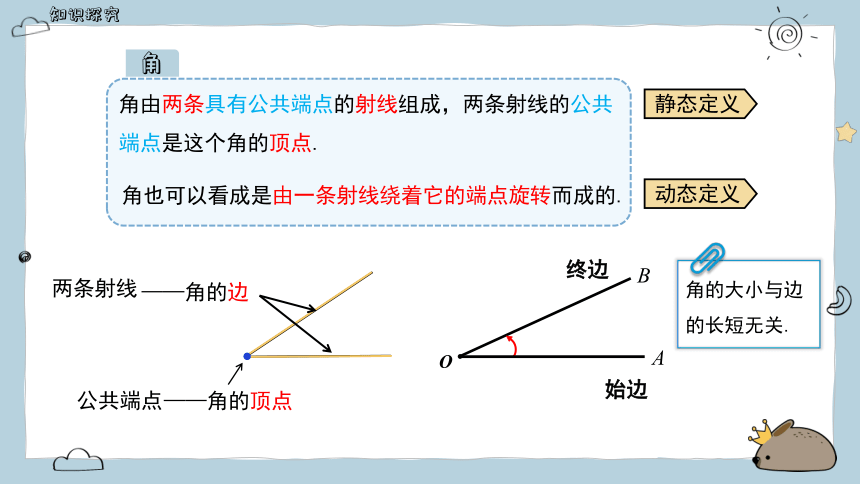
角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点.
公共端点
——角的顶点
两条射线
——角的边
角也可以看成是由一条射线绕着它的端点旋转而成的.
始边
终边
O
A
B
角的大小与边的长短无关.
静态定义
动态定义
知识探究
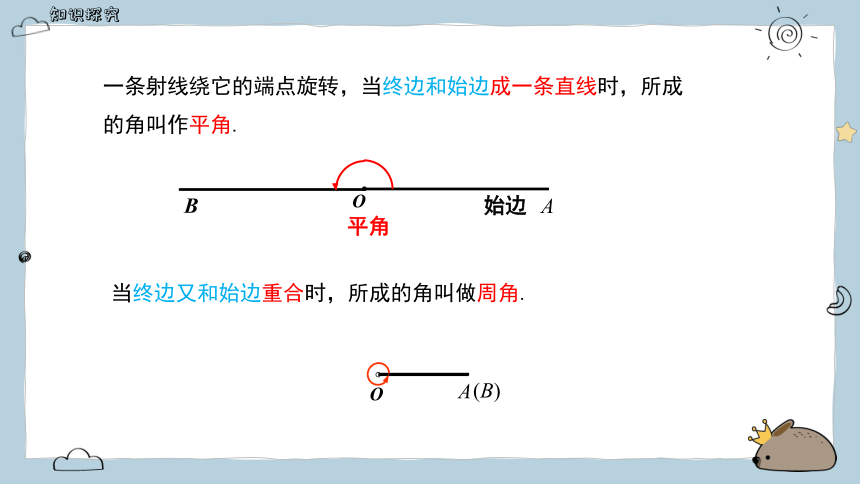
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫作平角.
始边
O
A
B
平角
当终边又和始边重合时,所成的角叫做周角.
O
A
(B)
知识探究
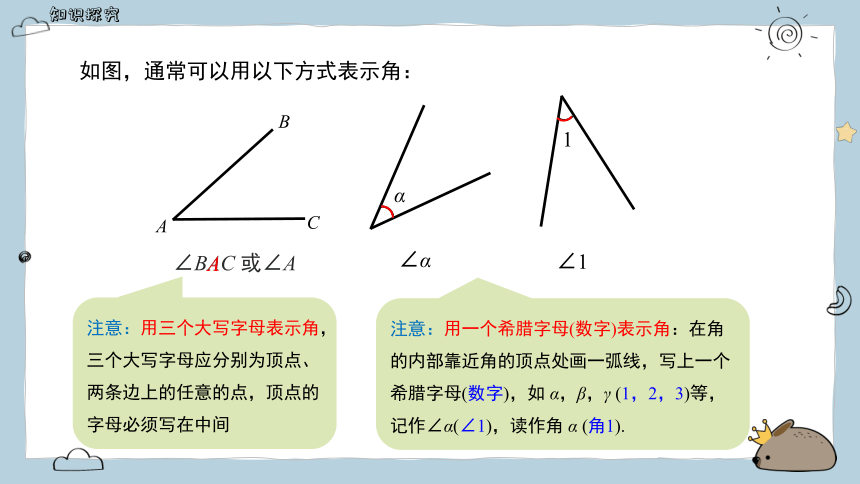
如图,通常可以用以下方式表示角:
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
注意:用一个希腊字母(数字)表示角:在角的内部靠近角的顶点处画一弧线,写上一个希腊字母(数字),如 α,β,γ (1,2,3)等,记作∠α(∠1),读作角 α (角1).
注意:用三个大写字母表示角,三个大写字母应分别为顶点、两条边上的任意的点,顶点的字母必须写在中间
A
知识探究
尝试·思考
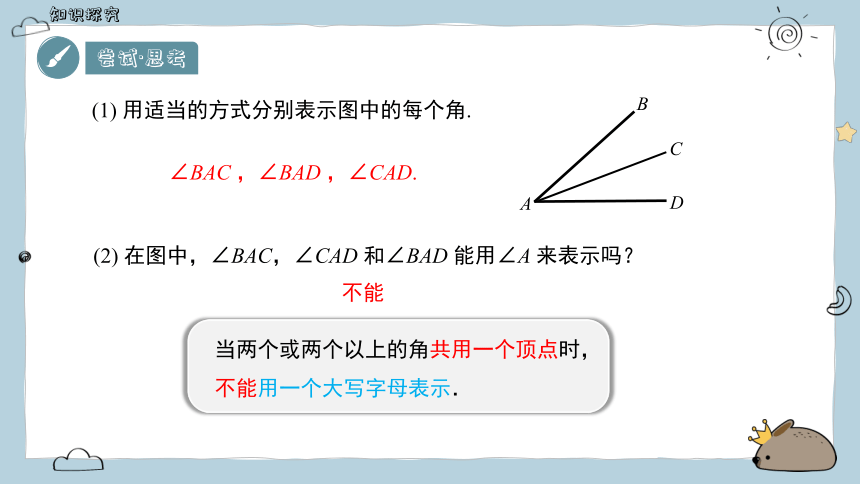
(1) 用适当的方式分别表示图中的每个角.
∠BAC ,∠BAD ,∠CAD.
(2) 在图中,∠BAC,∠CAD 和∠BAD 能用∠A 来表示吗?
不能
当两个或两个以上的角共用一个顶点时,不能用一个大写字母表示.
B
D
A
C
知识探究
和线段一样,在学习了角的表示方法后,我们也要学习如何度量角的大小.
在小学我们已经知道:1 周角=360°,1 平角=180°,1 直角=90°.
为了更精密地度量角,我们规定:
思考·交流
1°的 为 1 分,记作 1′,即 1°=60′.
1′ 的 为 1 秒,记作 1″,即 1′=60″.
典型例题
例1 计算:
(1)1.45°等于多少分?等于多少秒?
(2)1800″ 等于多少分?等于多少度?
解:(1) 60′×1.45=87′,
即 1.45°=87′=5220″;
(2) ()′ ×1800=30′ ,
60″×87=5 220″,
()°×30 =0.5°,
即 1800″=30′=0.5°.
知识探究
右图呈现了几个城市在中国地图上的大致位置.
分别用点O,A,B,C,D表示北京,哈尔滨,上海,福州,西安的位置,可得以北京为中心的每两个城市之间的夹角分别是∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD.
观察·思考
(1) 分别表示以北京为中心的每两个城市之间的夹角.
A
O
B
C
D
知识探究
方位角
在小学的时候,同学们学习过表示方向的角,我们用两条相互垂直的直线来代表南北和东西,即上北下南,左西右东.
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位:
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
知识探究
方位角
表示方向的角(方位角)在航行、测绘等工作中经常用到.
东北方向表示北偏东45°,
西北方向表示北偏西45°,
东南方向表示南偏东45°,
西南方向表示南偏西45°.
注意:方位角通常先写北或南,再写偏东或偏西,如“北偏东30°”一般不写成“东偏北60°”.
知识探究
右图呈现了几个城市在中国地图上的大致位置.
观察可知,哈尔滨在北京的北偏东约45°.
观察·思考
(2) 哈尔滨在北京的北偏东大约多少度?
A
O
B
C
D
东
当堂检测
D
A
A
B
B
D
67.5
南偏西40°
相等
角的定义:
角的表示方法:
角
角的度量:单位:度、分、秒.
角由两条具有公共端点的射线组成.
角也可以看成是由一条射线绕着它的端点旋转而成的.
1°=60′,1′=60″ .
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
感谢观看
4.2角
(第 1 课时)
第四章 基本平面图形
北师大版(2024)七年级上册
学习目标
理解角的概念,掌握角的表示方法
01
理解平角、周角的概念,掌握角的常用度量单位:度、分、秒,及它们之间的换算关系,并会进行简单的换算
02
知识引入
在小学我们学习过角,请说说你对角的认识. 你能在下图中找到角吗?
都有两条边和一个顶点.
知识探究
角
角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点.
公共端点
——角的顶点
两条射线
——角的边
角也可以看成是由一条射线绕着它的端点旋转而成的.
始边
终边
O
A
B
角的大小与边的长短无关.
静态定义
动态定义
知识探究
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫作平角.
始边
O
A
B
平角
当终边又和始边重合时,所成的角叫做周角.
O
A
(B)
知识探究
如图,通常可以用以下方式表示角:
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
注意:用一个希腊字母(数字)表示角:在角的内部靠近角的顶点处画一弧线,写上一个希腊字母(数字),如 α,β,γ (1,2,3)等,记作∠α(∠1),读作角 α (角1).
注意:用三个大写字母表示角,三个大写字母应分别为顶点、两条边上的任意的点,顶点的字母必须写在中间
A
知识探究
尝试·思考
(1) 用适当的方式分别表示图中的每个角.
∠BAC ,∠BAD ,∠CAD.
(2) 在图中,∠BAC,∠CAD 和∠BAD 能用∠A 来表示吗?
不能
当两个或两个以上的角共用一个顶点时,不能用一个大写字母表示.
B
D
A
C
知识探究
和线段一样,在学习了角的表示方法后,我们也要学习如何度量角的大小.
在小学我们已经知道:1 周角=360°,1 平角=180°,1 直角=90°.
为了更精密地度量角,我们规定:
思考·交流
1°的 为 1 分,记作 1′,即 1°=60′.
1′ 的 为 1 秒,记作 1″,即 1′=60″.
典型例题
例1 计算:
(1)1.45°等于多少分?等于多少秒?
(2)1800″ 等于多少分?等于多少度?
解:(1) 60′×1.45=87′,
即 1.45°=87′=5220″;
(2) ()′ ×1800=30′ ,
60″×87=5 220″,
()°×30 =0.5°,
即 1800″=30′=0.5°.
知识探究
右图呈现了几个城市在中国地图上的大致位置.
分别用点O,A,B,C,D表示北京,哈尔滨,上海,福州,西安的位置,可得以北京为中心的每两个城市之间的夹角分别是∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD.
观察·思考
(1) 分别表示以北京为中心的每两个城市之间的夹角.
A
O
B
C
D
知识探究
方位角
在小学的时候,同学们学习过表示方向的角,我们用两条相互垂直的直线来代表南北和东西,即上北下南,左西右东.
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位:
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
知识探究
方位角
表示方向的角(方位角)在航行、测绘等工作中经常用到.
东北方向表示北偏东45°,
西北方向表示北偏西45°,
东南方向表示南偏东45°,
西南方向表示南偏西45°.
注意:方位角通常先写北或南,再写偏东或偏西,如“北偏东30°”一般不写成“东偏北60°”.
知识探究
右图呈现了几个城市在中国地图上的大致位置.
观察可知,哈尔滨在北京的北偏东约45°.
观察·思考
(2) 哈尔滨在北京的北偏东大约多少度?
A
O
B
C
D
东
当堂检测
D
A
A
B
B
D
67.5
南偏西40°
相等
角的定义:
角的表示方法:
角
角的度量:单位:度、分、秒.
角由两条具有公共端点的射线组成.
角也可以看成是由一条射线绕着它的端点旋转而成的.
1°=60′,1′=60″ .
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
感谢观看
同课章节目录
