浙江省金华市2025年七年级下册期末考试数学模拟卷 含解析
文档属性
| 名称 | 浙江省金华市2025年七年级下册期末考试数学模拟卷 含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 665.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 17:04:41 | ||
图片预览




文档简介
/ 让教学更有效 精品试卷 | 数学学科
浙江省金华市2025年七年级下册期末考试数学模拟卷
满分120分 时间120分钟
一、选择题(共30分)
1.2025年第九届亚洲冬季运动会的吉祥物是一对可爱的东北虎“滨滨”和“妮妮”.如图,通过平移吉祥物,可以得到的图形是( )(不考虑由于印刷而导致的颜色变化)
A. B. C. D.
2.下面调查统计中,适合做普查的是( )
A.某品牌电冰箱的市场占有率 B.某个社区居民对垃圾分类的知晓率
C.某品牌汽车每百公里的耗油量 D.今天班主任张老师与几名同学谈话
3.用加减消元法解方程组时,如果想消掉x,操作正确的是()
A. B. C. D.
4.下列能用平方差公式因式分解的是( )
A. B. C. D.
5.根据下列表格中的信息,代表的分式可能是( )
… 0 1 2 …
… 0 无意义 * 无意义 * …
A. B. C. D.
6.如图,下列条件:①;②;③;④;⑤.其中,能判定的条件有( )
A.5个 B.4个 C.3个 D.2个
7.姜山镇要修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村,水渠从村沿方向修建到村,且保持.一工程队从村沿开始施工,施工方向是( )
A.北偏东 B.北偏东 C.南偏西 D.南偏西
8.若,则的值为( )
A. B. C. D.
9.在古代建筑中,榫()卯()结构至关重要,它通过凸出的榫头和凹进的榫眼精密配合连接,使得建筑物连接牢固且难以松动.工匠们制作一种特定的榫卯组合,每个榫头需要耗费的木材比每个榫眼需要耗费的木材多千克.已知用30千克木材制作榫头的数量与用25千克木材制作榫眼的数量相同.设制作1个榫头需要耗费的木材为x千克,则可列方程为( )
A. B. C. D.
10.“杨辉三角”(如图),也叫“贾宪三角”,是中国古代数学无比睿智的成就之一,被后世广泛运用.用“杨辉三角”可以解释(,2,3,4)的展开式(按a的次数由大到小的顺序)的系数规律,例如,在“杨辉三角”中第3行的3个数1,2,1,恰好对应着的展开式中各项的系数;第4行的4个数1,3,3,1,恰好对应着的展开式中各项的系数,等等.当n是大于4的自然数时,上述规律仍然成立.则下列说法正确的有( )个
①的展开式中的系数是9
②的展开式为:
③能被28整除
A.0 B.1 C.2 D.3
二、填空题(共18分)
11.分解因式: .
12.一本书某页有1200字,小红发现“的”字出现36次,该页书中出现“的”字的频率是 .
13.分式与的最简公分母是 .
14.如图,的周长是,现将向左平移得到,交于点G,那么四边形的周长是 .
15.若的计算结果不含的一次项,则的值为 .
16.若关于的二元一次方程组的解是,则关于的二元一次方程组的解是 .
三、解答题(共72分)
17.(8分)解方程组:.
18.(8分)计算:
(1);
(2)化简:.
19.(8分)如图,已知于点E,于点G,,能成立吗?为什么?
20.(8分)因式分解:
(1);
(2).
21.(8分)先化简,再求值:,其中.
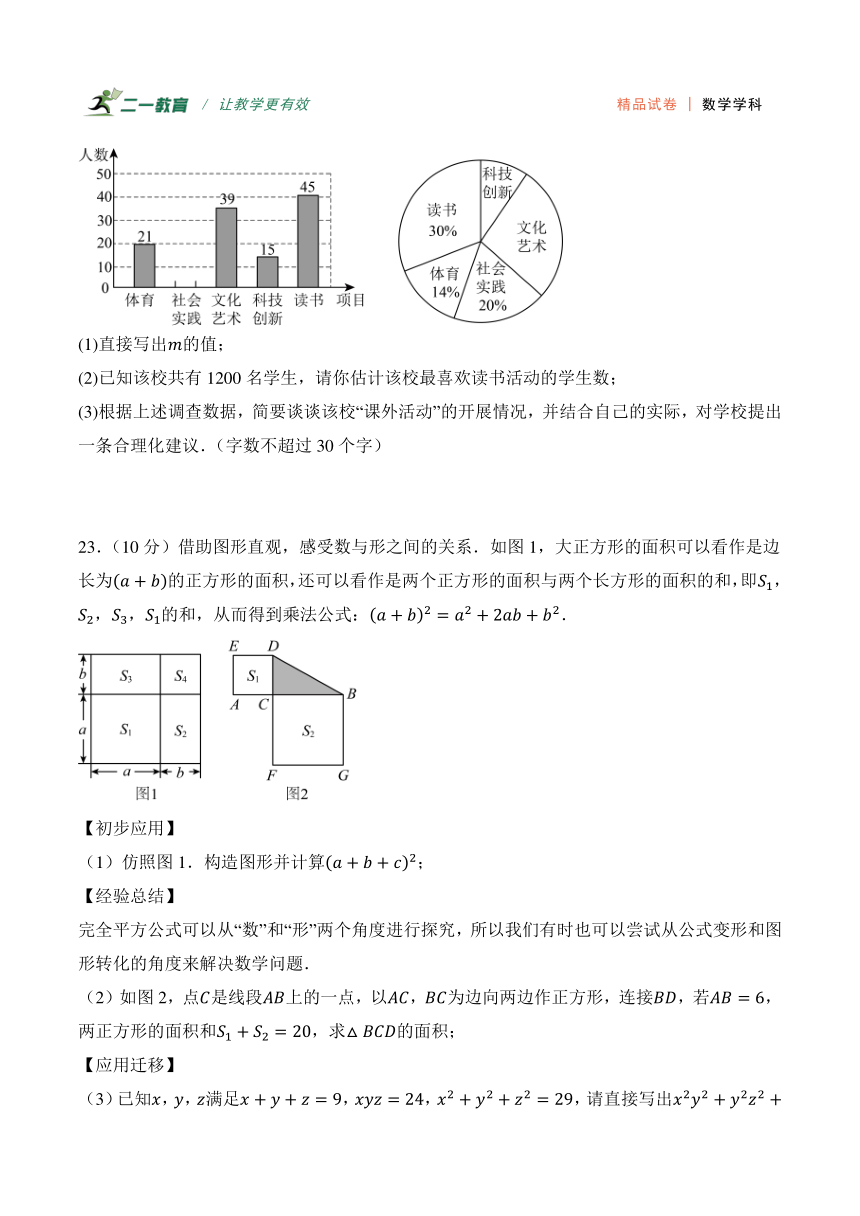
22.(10分)某校为了有效提升学生综合素质,同时减轻学生课业负担,决定在全校开展丰富多彩的学生课外活动,经研究确定课外活动类型为体育、社会实践、文化艺术、科技创新和读书等五类项目,学生从中选最感兴趣的一项活动参加.并在组织活动前作了调查,随机抽查了名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
(1)直接写出的值;
(2)已知该校共有1200名学生,请你估计该校最喜欢读书活动的学生数;
(3)根据上述调查数据,简要谈谈该校“课外活动”的开展情况,并结合自己的实际,对学校提出一条合理化建议.(字数不超过30个字)
23.(10分)借助图形直观,感受数与形之间的关系.如图1,大正方形的面积可以看作是边长为的正方形的面积,还可以看作是两个正方形的面积与两个长方形的面积的和,即,,,的和,从而得到乘法公式:.
【初步应用】
(1)仿照图1.构造图形并计算;
【经验总结】
完全平方公式可以从“数”和“形”两个角度进行探究,所以我们有时也可以尝试从公式变形和图形转化的角度来解决数学问题.
(2)如图2,点是线段上的一点,以,为边向两边作正方形,连接,若,两正方形的面积和,求的面积;
【应用迁移】
(3)已知,,满足,,,请直接写出的值.
24.(12分)问题情境:综合实践课上,王老师组织同学们开展了探究三角之间数量关系的数学活动.
(1)如图1,,点A,B分别为直线上的一点,点为平行线间一点且,,求度数;
问题迁移:
(2)如图2,射线与射线交于点,直线,直线分别交,于点,直线分别交于点,点在射线上运动.
①当点在(不与重合)两点之间运动时,设,.则之间有何数量关系?
②若点不在线段上运动时(点与点三点都不重合),请直接写出间的数量关系.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D A D D C C C A D
1.B
【分析】根据平移的性质,平移不改变图形的形状、大小和方向,只需逐一分析选项中图形与原吉祥物图形的形状、方向等是否一致,找出符合平移特征的图形.本题主要考查了平移的性质,熟练掌握平移不改变图形的形状、大小和方向是解题的关键.
【详解】解:平移的性质是图形平移后,形状、大小、方向均不变,只是位置发生变化.
选项A:图形方向与原吉祥物不同,不是平移得到.
选项B:图形的形状、大小、方向与原吉祥物一致,是平移得到.
选项C:图形方向与原吉祥物不同,不是平移得到.
选项D:图形方向与原吉祥物不同,不是平移得到.
故选:B.
2.D
【分析】本题考查抽样调查和全面调查的区别,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.解题的关键是掌握:选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
【详解】解:A.某品牌电冰箱的市场占有率,适合抽样调查,故此选项不符合题意;
B.某个社区居民对垃圾分类的知晓率,适合抽样调查,故此选项不符合题意;
C.某品牌汽车每百公里的耗油量,适合抽样调查,故此选项不符合题意;
D.今天班主任张老师与几名同学谈话,适合普查,故此选项符合题意.
故选:D.
3.A
【分析】本题考查加减消元法解方程组.利用加减消元法解方程组即可.
【详解】解∶A.得,可以消掉x,故操作正确;
B.得,不可以消掉x,故操作错误;
C.得,不可以消掉x,故操作错误;
D.得,不可以消掉x,故操作错误;
故选:A.
4.D
【分析】此题主要考查了平方差公式,关键是熟练掌握平方差公式分解因式的多项式的特点.根据能够运用平方差公式分解因式的多项式必须是二项式,两项都能写成平方的形式,且符号相反进行判断即可.
【详解】解:A、是与1的和,不能用平方差公式进行分解,故此选项错误;
B、共有三项,不能用平方差公式进行分解,故此选项错误;
C、两项的符号不相反,不能用平方差公式进行分解,故此选项错误;
D、符合平方差公式特点,能用平方差公式进行分解,故此选项正确;
故选:D.
5.D
【分析】本题考查了分式有意义的条件,根据分式有意义的条件及分式的值为的条件解答即可,熟知分式有意义的条件是分母不等于零是解题的关键.
【详解】解:由表格可知,当时分式无意义,
∴A不合题意;
∵当时,分式无意义,
∴B不合题意;
∵时分式的值为,
∴C不符合题意,D符合题意,
故选:D.
6.C
【分析】本题考查了平行线的判定定理,根据平行线的判定定理逐项分析即可得解,熟练掌握平行线的判定定理是解此题的关键.
【详解】解:①∵,∴,故①符合题意;
②∵,∴,故②不符合题意;
③∵,∴,故③不符合题意;
④∵,∴,故④符合题意;
⑤∵,∴,故⑤符合题意;
综上所述,正确的有①④⑤,共个,
故选:C.
7.C
【分析】本题考查了平行线的性质,方向角,根据题目的已知条件并结合图形进行分析是解题的关键.利用平行线的性质,结合图形即可求解.
【详解】解:∵,水渠从村沿北偏东方向到村,
∴从村沿的方向是南偏西
故选:C.
8.C
【分析】本题考查了同底数幂乘法的逆运算,幂的乘方的逆运算,根据同底数幂乘法的逆运算和幂的乘方的逆运算可得,进而代入已知计算即可求解,掌握以上知识点是解题的关键.
【详解】解:∵,
∴,
故选:.
9.A
【分析】本题主要考查了分式方程的实际应用,设制作1个榫头需要耗费的木材为x千克,则制作1个榫眼需要耗费的木材为x千克,再根据用30千克木材制作榫头的数量与用25千克木材制作榫眼的数量相同建立方程即可.
【详解】解:设制作1个榫头需要耗费的木材为x千克,
由题意得,,
故选:A.
10.D
【分析】本题考查数字的变换类规律,解题的关键是读懂题意,找到“杨辉三角”的规律.求出的展开式中的系数即可判定①;由计算规律可判断②正确;将分解为,再将分解成即可判定.
【详解】解:由计算规律可得,的展开式中,字母部分因式依次为,,,…,
∴含的为第二项,
又由“杨辉三角”可知,的展开式中第二项的系数为n,
∴的展开式中含的项为,故①正确;
由计算规律可得,
,故②正确;
∵,
而
,
∴能被28整除,故③正确;
∴正确的有①②③,共3个;
故选:D.
11./
【分析】本题考查了提取公因式法分解因式,掌握提取公因式法是关键.
根据题意提取公因式,进行分解即可.
【详解】解:,
故答案为: .
12./
【分析】本题主要考查了频率的计算公式:频率频数数据总和,是需要识记的内容.根据频数和频率的定义求解.
【详解】解:由题意可得,
即该页书中出现“的”字的频率是,
故答案为:
13./
【分析】本题考查了最简公分母,解题的关键是掌握确定最简公分母的一般方法:①如果各分母都是单项式,那么最简公分母就是各项系数的最小公倍数和所有字母的最高次幂的积,②如果各分母都是多项式,先把它们分解因式,然后把每个因式当做一个字母,再从系数、相同字母求最简公分母.
根据求最简公分母的方法求解即可.
【详解】解:分式与的最简公分母.
故答案为:.
14.17
【分析】本题主要考查了平移的性质、周长公式等知识点,熟练掌握平移的性质是解题的关键.
由平移的性质得到,,然后根据三角形的面积公式以及四边形的面积公式求解即可.
【详解】解:∵将向左平移得到,
∴,,
∵的周长是11cm,
∴,
∴四边形的周长是.
故答案为:17.
15.
【分析】本题考查已知多项式乘积不含某项求字母的值,掌握多项式乘积不含某项,即该项系数等于0是解题的关键.
先根据多项式乘以多项式法则计算,再根据计算结果不含的一次项,得出含的一次项的系数为0,建立关于a的方程求解即可.
【详解】解:
,
∵的计算结果不含的一次项,
∴,
解得:,
故答案为:.
16.
【分析】本题考查了二元一次方程组的解:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解,也考查了解二元一次方程组.二元一次方程组的解看成,解出x,y即可.
【详解】解:∵二元一次方程组的解是,
∴把关于二元一次方程组看作关于和 的二元一次方程组,
∴,
解得:,
则二元一次方程组的解是,
故答案为:
17.
【分析】本题考查了解二元一次方程组,利用加减法解答即可求解,掌握解二元一次方程组的方法是解题的关键.
【详解】解:① ②,得,
解得,
将代入①,得,
解得,
∴方程组的解为.
18.(1);
(2)
【分析】本题主要考查了整式混合运算和实数混合运算,解题的关键是熟练掌握乘方运算法则,零指数幂和负整数幂进行运算法则和平方差公式,准确计算.
(1)根据乘方运算法则,零指数幂和负整数幂进行运算即可;
(2)先利用平方差公式进行运算,再合并同类项即可.
【详解】(1)解:原式;
(2)解:原式 .
19.见解析
【分析】根据,,得出,得出,根据余角的性质得出,根据平行线的判定得出.
【详解】证明:∵,,
∴,
∴,
∵,
∴,
∴.
【点睛】本题主要考查了垂线的定义,余角的性质,平行线的判定,解题的关键是熟练掌握平行线的判定方法,内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.
20.(1)
(2)
【分析】本题主要考查了因式分解,综合运用提取公因式法和公式法进行因式分解成为解题的关键.
(1)先提取公因式,然后运用平方差公式因式分解即可;
(2)先提取公因式,然后运用完全平方公式因式分解即可.
【详解】(1)解:.
(2)解:.
21.,
【分析】本题考查了分式的化简求值,完全平方公式以及平方差公式的运用,熟练掌握分式的运算法则是关键.本题考查了分式的化简求值,熟练掌握分式的运算法则是关键.
【详解】解:
,
当时,原式.
22.(1)150
(2)360名
(3)见解析(答案不唯一)
【分析】本题考查了条形统计图和扇形统计图的综合运用,样本估计总体.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
(1)用最喜欢读书的人数除以它占的百分比得到的值;
(2)利用样本估计总体,用1200乘样本中最喜欢读书活动的学生数所占的百分比即可;
(3)建议有积极意义即可.
【详解】(1)解: ;
(2)解:(名,
答:估计该校最喜欢读书活动的学生数为360名;
(3)解:对于课外活动,喜欢“文化艺术”和“读书”的较多,我认为学校要加强科技创新宣传,并提供相应条件,促进科技创新活动的开展.(答案不唯一,建议有积极意义即可).
23.(1);(2)4;(3)244
【分析】本题考查的是完全平方公式及其变形的应用,已知式子的值求代数式的值,正确掌握相关性质内容是解题的关键.
(1)直接作图即可得出即可;
(2)设,,由题意可得,,再结合完全平方公式的变形可得答案;
(3)由可得,结合,再代入数值计算,可得答案.
【详解】解:(1)如图,已知大正方形的边长为,
利用图形3的面积关系可得:.
(2)依题意,设,,
∵以,为边向两边作正方形,连接,,两正方形的面积和
∴,
∵
.
(3)与(1)同理得,
∵,,,
∴
,
同理得
∴
.
24.(1);(2)①当点在A,B(不与A,B重合)两点之间运动时,;②当在延长线时,;当在之间时,
【分析】本题主要考查了平行线的性质与判定,正确的作出辅助线、灵活运用平行线的性质成为解题的关键.
(1)如图:过作,则,根据平行线的性质得出,再将已知条件代入即可解答;
(2)①同(1)求解即可;②如图:当在延长线时,过作交于,结合图形可得;同理:可求当在之间时.
【详解】(1)解:如图:过作,
∵,
∴,
∴,
∴,
即,
∵,
∴;
(2)解 :①,理由如下:
如图:过作交于,
,
,
,
;
②如图:当 P 在延长线时,
如图:过作交延长线于,
,
,
,
如图:当在之间时,
如图:过作交于,
,
,
,
.
浙江省金华市2025年七年级下册期末考试数学模拟卷
满分120分 时间120分钟
一、选择题(共30分)
1.2025年第九届亚洲冬季运动会的吉祥物是一对可爱的东北虎“滨滨”和“妮妮”.如图,通过平移吉祥物,可以得到的图形是( )(不考虑由于印刷而导致的颜色变化)
A. B. C. D.
2.下面调查统计中,适合做普查的是( )
A.某品牌电冰箱的市场占有率 B.某个社区居民对垃圾分类的知晓率
C.某品牌汽车每百公里的耗油量 D.今天班主任张老师与几名同学谈话
3.用加减消元法解方程组时,如果想消掉x,操作正确的是()
A. B. C. D.
4.下列能用平方差公式因式分解的是( )
A. B. C. D.
5.根据下列表格中的信息,代表的分式可能是( )
… 0 1 2 …
… 0 无意义 * 无意义 * …
A. B. C. D.
6.如图,下列条件:①;②;③;④;⑤.其中,能判定的条件有( )
A.5个 B.4个 C.3个 D.2个
7.姜山镇要修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村,水渠从村沿方向修建到村,且保持.一工程队从村沿开始施工,施工方向是( )
A.北偏东 B.北偏东 C.南偏西 D.南偏西
8.若,则的值为( )
A. B. C. D.
9.在古代建筑中,榫()卯()结构至关重要,它通过凸出的榫头和凹进的榫眼精密配合连接,使得建筑物连接牢固且难以松动.工匠们制作一种特定的榫卯组合,每个榫头需要耗费的木材比每个榫眼需要耗费的木材多千克.已知用30千克木材制作榫头的数量与用25千克木材制作榫眼的数量相同.设制作1个榫头需要耗费的木材为x千克,则可列方程为( )
A. B. C. D.
10.“杨辉三角”(如图),也叫“贾宪三角”,是中国古代数学无比睿智的成就之一,被后世广泛运用.用“杨辉三角”可以解释(,2,3,4)的展开式(按a的次数由大到小的顺序)的系数规律,例如,在“杨辉三角”中第3行的3个数1,2,1,恰好对应着的展开式中各项的系数;第4行的4个数1,3,3,1,恰好对应着的展开式中各项的系数,等等.当n是大于4的自然数时,上述规律仍然成立.则下列说法正确的有( )个
①的展开式中的系数是9
②的展开式为:
③能被28整除
A.0 B.1 C.2 D.3
二、填空题(共18分)
11.分解因式: .
12.一本书某页有1200字,小红发现“的”字出现36次,该页书中出现“的”字的频率是 .
13.分式与的最简公分母是 .
14.如图,的周长是,现将向左平移得到,交于点G,那么四边形的周长是 .
15.若的计算结果不含的一次项,则的值为 .
16.若关于的二元一次方程组的解是,则关于的二元一次方程组的解是 .
三、解答题(共72分)
17.(8分)解方程组:.
18.(8分)计算:
(1);
(2)化简:.
19.(8分)如图,已知于点E,于点G,,能成立吗?为什么?
20.(8分)因式分解:
(1);
(2).
21.(8分)先化简,再求值:,其中.
22.(10分)某校为了有效提升学生综合素质,同时减轻学生课业负担,决定在全校开展丰富多彩的学生课外活动,经研究确定课外活动类型为体育、社会实践、文化艺术、科技创新和读书等五类项目,学生从中选最感兴趣的一项活动参加.并在组织活动前作了调查,随机抽查了名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
(1)直接写出的值;
(2)已知该校共有1200名学生,请你估计该校最喜欢读书活动的学生数;
(3)根据上述调查数据,简要谈谈该校“课外活动”的开展情况,并结合自己的实际,对学校提出一条合理化建议.(字数不超过30个字)
23.(10分)借助图形直观,感受数与形之间的关系.如图1,大正方形的面积可以看作是边长为的正方形的面积,还可以看作是两个正方形的面积与两个长方形的面积的和,即,,,的和,从而得到乘法公式:.
【初步应用】
(1)仿照图1.构造图形并计算;
【经验总结】
完全平方公式可以从“数”和“形”两个角度进行探究,所以我们有时也可以尝试从公式变形和图形转化的角度来解决数学问题.
(2)如图2,点是线段上的一点,以,为边向两边作正方形,连接,若,两正方形的面积和,求的面积;
【应用迁移】
(3)已知,,满足,,,请直接写出的值.
24.(12分)问题情境:综合实践课上,王老师组织同学们开展了探究三角之间数量关系的数学活动.
(1)如图1,,点A,B分别为直线上的一点,点为平行线间一点且,,求度数;
问题迁移:
(2)如图2,射线与射线交于点,直线,直线分别交,于点,直线分别交于点,点在射线上运动.
①当点在(不与重合)两点之间运动时,设,.则之间有何数量关系?
②若点不在线段上运动时(点与点三点都不重合),请直接写出间的数量关系.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D A D D C C C A D
1.B
【分析】根据平移的性质,平移不改变图形的形状、大小和方向,只需逐一分析选项中图形与原吉祥物图形的形状、方向等是否一致,找出符合平移特征的图形.本题主要考查了平移的性质,熟练掌握平移不改变图形的形状、大小和方向是解题的关键.
【详解】解:平移的性质是图形平移后,形状、大小、方向均不变,只是位置发生变化.
选项A:图形方向与原吉祥物不同,不是平移得到.
选项B:图形的形状、大小、方向与原吉祥物一致,是平移得到.
选项C:图形方向与原吉祥物不同,不是平移得到.
选项D:图形方向与原吉祥物不同,不是平移得到.
故选:B.
2.D
【分析】本题考查抽样调查和全面调查的区别,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.解题的关键是掌握:选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
【详解】解:A.某品牌电冰箱的市场占有率,适合抽样调查,故此选项不符合题意;
B.某个社区居民对垃圾分类的知晓率,适合抽样调查,故此选项不符合题意;
C.某品牌汽车每百公里的耗油量,适合抽样调查,故此选项不符合题意;
D.今天班主任张老师与几名同学谈话,适合普查,故此选项符合题意.
故选:D.
3.A
【分析】本题考查加减消元法解方程组.利用加减消元法解方程组即可.
【详解】解∶A.得,可以消掉x,故操作正确;
B.得,不可以消掉x,故操作错误;
C.得,不可以消掉x,故操作错误;
D.得,不可以消掉x,故操作错误;
故选:A.
4.D
【分析】此题主要考查了平方差公式,关键是熟练掌握平方差公式分解因式的多项式的特点.根据能够运用平方差公式分解因式的多项式必须是二项式,两项都能写成平方的形式,且符号相反进行判断即可.
【详解】解:A、是与1的和,不能用平方差公式进行分解,故此选项错误;
B、共有三项,不能用平方差公式进行分解,故此选项错误;
C、两项的符号不相反,不能用平方差公式进行分解,故此选项错误;
D、符合平方差公式特点,能用平方差公式进行分解,故此选项正确;
故选:D.
5.D
【分析】本题考查了分式有意义的条件,根据分式有意义的条件及分式的值为的条件解答即可,熟知分式有意义的条件是分母不等于零是解题的关键.
【详解】解:由表格可知,当时分式无意义,
∴A不合题意;
∵当时,分式无意义,
∴B不合题意;
∵时分式的值为,
∴C不符合题意,D符合题意,
故选:D.
6.C
【分析】本题考查了平行线的判定定理,根据平行线的判定定理逐项分析即可得解,熟练掌握平行线的判定定理是解此题的关键.
【详解】解:①∵,∴,故①符合题意;
②∵,∴,故②不符合题意;
③∵,∴,故③不符合题意;
④∵,∴,故④符合题意;
⑤∵,∴,故⑤符合题意;
综上所述,正确的有①④⑤,共个,
故选:C.
7.C
【分析】本题考查了平行线的性质,方向角,根据题目的已知条件并结合图形进行分析是解题的关键.利用平行线的性质,结合图形即可求解.
【详解】解:∵,水渠从村沿北偏东方向到村,
∴从村沿的方向是南偏西
故选:C.
8.C
【分析】本题考查了同底数幂乘法的逆运算,幂的乘方的逆运算,根据同底数幂乘法的逆运算和幂的乘方的逆运算可得,进而代入已知计算即可求解,掌握以上知识点是解题的关键.
【详解】解:∵,
∴,
故选:.
9.A
【分析】本题主要考查了分式方程的实际应用,设制作1个榫头需要耗费的木材为x千克,则制作1个榫眼需要耗费的木材为x千克,再根据用30千克木材制作榫头的数量与用25千克木材制作榫眼的数量相同建立方程即可.
【详解】解:设制作1个榫头需要耗费的木材为x千克,
由题意得,,
故选:A.
10.D
【分析】本题考查数字的变换类规律,解题的关键是读懂题意,找到“杨辉三角”的规律.求出的展开式中的系数即可判定①;由计算规律可判断②正确;将分解为,再将分解成即可判定.
【详解】解:由计算规律可得,的展开式中,字母部分因式依次为,,,…,
∴含的为第二项,
又由“杨辉三角”可知,的展开式中第二项的系数为n,
∴的展开式中含的项为,故①正确;
由计算规律可得,
,故②正确;
∵,
而
,
∴能被28整除,故③正确;
∴正确的有①②③,共3个;
故选:D.
11./
【分析】本题考查了提取公因式法分解因式,掌握提取公因式法是关键.
根据题意提取公因式,进行分解即可.
【详解】解:,
故答案为: .
12./
【分析】本题主要考查了频率的计算公式:频率频数数据总和,是需要识记的内容.根据频数和频率的定义求解.
【详解】解:由题意可得,
即该页书中出现“的”字的频率是,
故答案为:
13./
【分析】本题考查了最简公分母,解题的关键是掌握确定最简公分母的一般方法:①如果各分母都是单项式,那么最简公分母就是各项系数的最小公倍数和所有字母的最高次幂的积,②如果各分母都是多项式,先把它们分解因式,然后把每个因式当做一个字母,再从系数、相同字母求最简公分母.
根据求最简公分母的方法求解即可.
【详解】解:分式与的最简公分母.
故答案为:.
14.17
【分析】本题主要考查了平移的性质、周长公式等知识点,熟练掌握平移的性质是解题的关键.
由平移的性质得到,,然后根据三角形的面积公式以及四边形的面积公式求解即可.
【详解】解:∵将向左平移得到,
∴,,
∵的周长是11cm,
∴,
∴四边形的周长是.
故答案为:17.
15.
【分析】本题考查已知多项式乘积不含某项求字母的值,掌握多项式乘积不含某项,即该项系数等于0是解题的关键.
先根据多项式乘以多项式法则计算,再根据计算结果不含的一次项,得出含的一次项的系数为0,建立关于a的方程求解即可.
【详解】解:
,
∵的计算结果不含的一次项,
∴,
解得:,
故答案为:.
16.
【分析】本题考查了二元一次方程组的解:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解,也考查了解二元一次方程组.二元一次方程组的解看成,解出x,y即可.
【详解】解:∵二元一次方程组的解是,
∴把关于二元一次方程组看作关于和 的二元一次方程组,
∴,
解得:,
则二元一次方程组的解是,
故答案为:
17.
【分析】本题考查了解二元一次方程组,利用加减法解答即可求解,掌握解二元一次方程组的方法是解题的关键.
【详解】解:① ②,得,
解得,
将代入①,得,
解得,
∴方程组的解为.
18.(1);
(2)
【分析】本题主要考查了整式混合运算和实数混合运算,解题的关键是熟练掌握乘方运算法则,零指数幂和负整数幂进行运算法则和平方差公式,准确计算.
(1)根据乘方运算法则,零指数幂和负整数幂进行运算即可;
(2)先利用平方差公式进行运算,再合并同类项即可.
【详解】(1)解:原式;
(2)解:原式 .
19.见解析
【分析】根据,,得出,得出,根据余角的性质得出,根据平行线的判定得出.
【详解】证明:∵,,
∴,
∴,
∵,
∴,
∴.
【点睛】本题主要考查了垂线的定义,余角的性质,平行线的判定,解题的关键是熟练掌握平行线的判定方法,内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.
20.(1)
(2)
【分析】本题主要考查了因式分解,综合运用提取公因式法和公式法进行因式分解成为解题的关键.
(1)先提取公因式,然后运用平方差公式因式分解即可;
(2)先提取公因式,然后运用完全平方公式因式分解即可.
【详解】(1)解:.
(2)解:.
21.,
【分析】本题考查了分式的化简求值,完全平方公式以及平方差公式的运用,熟练掌握分式的运算法则是关键.本题考查了分式的化简求值,熟练掌握分式的运算法则是关键.
【详解】解:
,
当时,原式.
22.(1)150
(2)360名
(3)见解析(答案不唯一)
【分析】本题考查了条形统计图和扇形统计图的综合运用,样本估计总体.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
(1)用最喜欢读书的人数除以它占的百分比得到的值;
(2)利用样本估计总体,用1200乘样本中最喜欢读书活动的学生数所占的百分比即可;
(3)建议有积极意义即可.
【详解】(1)解: ;
(2)解:(名,
答:估计该校最喜欢读书活动的学生数为360名;
(3)解:对于课外活动,喜欢“文化艺术”和“读书”的较多,我认为学校要加强科技创新宣传,并提供相应条件,促进科技创新活动的开展.(答案不唯一,建议有积极意义即可).
23.(1);(2)4;(3)244
【分析】本题考查的是完全平方公式及其变形的应用,已知式子的值求代数式的值,正确掌握相关性质内容是解题的关键.
(1)直接作图即可得出即可;
(2)设,,由题意可得,,再结合完全平方公式的变形可得答案;
(3)由可得,结合,再代入数值计算,可得答案.
【详解】解:(1)如图,已知大正方形的边长为,
利用图形3的面积关系可得:.
(2)依题意,设,,
∵以,为边向两边作正方形,连接,,两正方形的面积和
∴,
∵
.
(3)与(1)同理得,
∵,,,
∴
,
同理得
∴
.
24.(1);(2)①当点在A,B(不与A,B重合)两点之间运动时,;②当在延长线时,;当在之间时,
【分析】本题主要考查了平行线的性质与判定,正确的作出辅助线、灵活运用平行线的性质成为解题的关键.
(1)如图:过作,则,根据平行线的性质得出,再将已知条件代入即可解答;
(2)①同(1)求解即可;②如图:当在延长线时,过作交于,结合图形可得;同理:可求当在之间时.
【详解】(1)解:如图:过作,
∵,
∴,
∴,
∴,
即,
∵,
∴;
(2)解 :①,理由如下:
如图:过作交于,
,
,
,
;
②如图:当 P 在延长线时,
如图:过作交延长线于,
,
,
,
如图:当在之间时,
如图:过作交于,
,
,
,
.
同课章节目录
