5.3 三次函数的图象与性质 课件 (共13张PPT)
文档属性
| 名称 | 5.3 三次函数的图象与性质 课件 (共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 17:37:29 | ||
图片预览




文档简介
(共13张PPT)
三次函数的图象与性质
教材版本:普通高中数学人教A版
授课教师: 学校:
形如
的函数叫做三次函数.
三次函数的概念:
探究:初识系数 a, b, c, d 的变化将怎样影响三次函数的图像与性质
①类比二次函数你能猜想哪个系数对函数的单调性没有影响?
②观察系数a变化时函数图象有何特征?
③当系数a >0时,系数b和c分别变化时,图象有
何特征?
思考:
利用信息技术工具画出三次函数
的图象,改变 a, b, c, d 的值,观察图象的形状并思考以下问题.
借助工具、尝试探究
图象
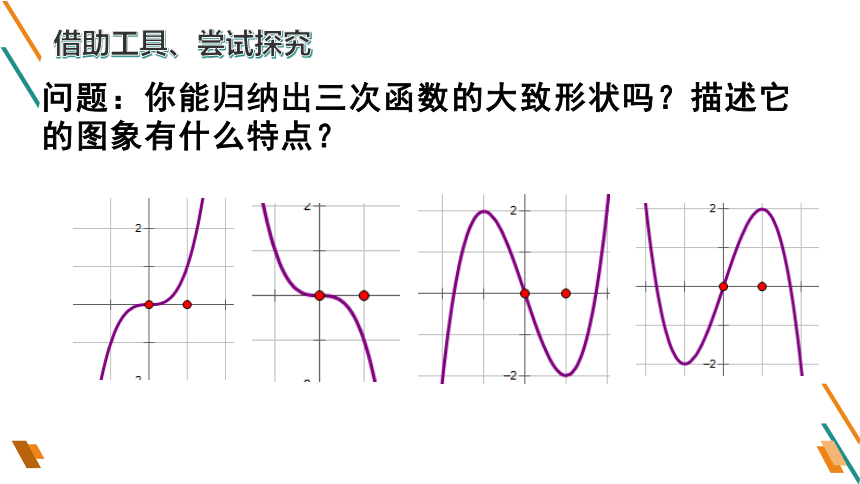
问题:你能归纳出三次函数的大致形状吗?描述它的图象有什么特点?
借助工具、尝试探究
我们通过数学软件观察了三次函数的图象,下面我们再用导数研究它的单调区间,若存在极值并求出相应的极值点.
设f (x)=ax3+bx2+cx+d (a≠0),则 f ′ (x) =3ax2+2bx+c是二次函数.可能有以下三种情形:
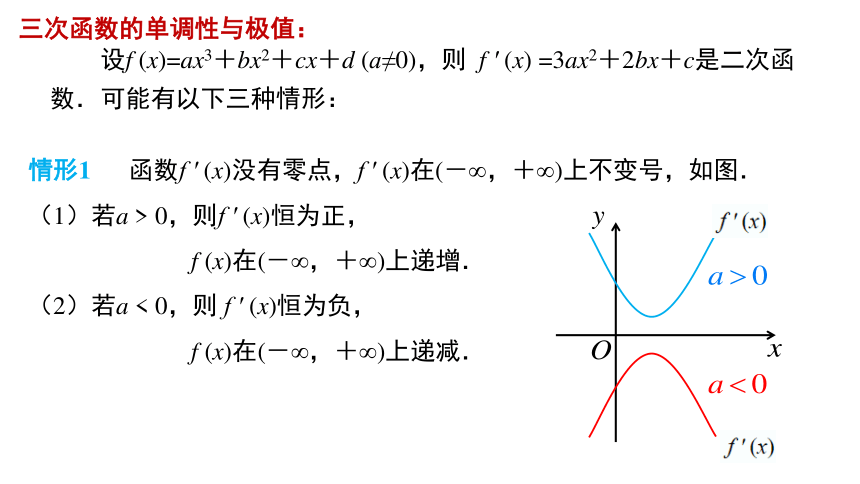
情形1 函数f ′ (x)没有零点,f ′ (x)在(-∞,+∞)上不变号,如图.
(1)若a > 0,则f ′ (x)恒为正,
f (x)在(-∞,+∞)上递增.
(2)若a < 0,则 f ′ (x)恒为负,
f (x)在(-∞,+∞)上递减.
三次函数的单调性与极值:
设f (x)=ax3+bx2+cx+d (a≠0),则f ′ (x)=3ax2+2bx+c是二次函数.
可能有以下三种情形:
情形2 函数f ′ (x)有一个零点x = w,如图.
(1)若a > 0,则f ′ (x)在(-∞,w)∪(w,+∞)恒为正,
f (x)在(-∞,+∞)上递增.
(2)若a < 0,则f ′ (x)在(-∞,w)∪(w,+∞)恒为负,
f (x)在(-∞,+∞)上递减.
三次函数的单调性与极值:
情形3 函数f ′ (x)有两个零点x1和x2,如图.
(1)若a > 0,则f ′ (x)在(-∞,x1)和(x2,+∞)为正,在(x1,x2)为负,
对应地, f (x) 在(-∞,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增.
由此可见f (x)在x = x1 处取得极大值,在x = x2 处取得极小值.
情形3 函数f ′ (x)有两个零点x = x1和x = x2,如图.
(2)若a < 0,则f ′ (x)在(-∞,x1)和(x2,+∞)为负,在(x1,x2)为正,
对应地, f (x)在(-∞,x1)上递减,在(x1,x2)上递增,在(x2,+∞)上递减.
由此可见f (x)在x = x1处取得极小值,在x = x2处取得极大值.
归 纳 总 结
三次函数的图象与性质
三次函数的单调性与极值:
设f (x)=ax3+bx2+cx+d (a≠0),则f ′ (x)=3ax2+2bx+c是二次函数.
f ′ (x)的判别式为 .
f ′ (x)的图像 f (x)的图像 f (x)的单调性 f (x)的极值
a>0 ≤0 在(-∞,+∞)上递增 无极值
>0 在(-∞,x1)上递增,在( x1 , x2 )上递减, 在(x2,+∞)上递增 极大值 f (x1)
极小值f (x2)
三次函数的单调性与极值:
设f (x)=ax3+bx2+cx+d (a≠0),则f ′ (x)=3ax2+2bx+c是二次函数.
f ′ (x)的判别式为 .
f ′ (x)的图像 f (x)的图像 f (x)的单调性 f (x)的极值
a<0 ≤0 在(-∞,+∞)上递减 无极值
>0 在(-∞,x1)上递减,在(x1,x2)上递增, 在(x2,+∞)上递减 极大值f (x2)
极小值f (x1)
谢谢!
三次函数的图象与性质
教材版本:普通高中数学人教A版
授课教师: 学校:
形如
的函数叫做三次函数.
三次函数的概念:
探究:初识系数 a, b, c, d 的变化将怎样影响三次函数的图像与性质
①类比二次函数你能猜想哪个系数对函数的单调性没有影响?
②观察系数a变化时函数图象有何特征?
③当系数a >0时,系数b和c分别变化时,图象有
何特征?
思考:
利用信息技术工具画出三次函数
的图象,改变 a, b, c, d 的值,观察图象的形状并思考以下问题.
借助工具、尝试探究
图象
问题:你能归纳出三次函数的大致形状吗?描述它的图象有什么特点?
借助工具、尝试探究
我们通过数学软件观察了三次函数的图象,下面我们再用导数研究它的单调区间,若存在极值并求出相应的极值点.
设f (x)=ax3+bx2+cx+d (a≠0),则 f ′ (x) =3ax2+2bx+c是二次函数.可能有以下三种情形:
情形1 函数f ′ (x)没有零点,f ′ (x)在(-∞,+∞)上不变号,如图.
(1)若a > 0,则f ′ (x)恒为正,
f (x)在(-∞,+∞)上递增.
(2)若a < 0,则 f ′ (x)恒为负,
f (x)在(-∞,+∞)上递减.
三次函数的单调性与极值:
设f (x)=ax3+bx2+cx+d (a≠0),则f ′ (x)=3ax2+2bx+c是二次函数.
可能有以下三种情形:
情形2 函数f ′ (x)有一个零点x = w,如图.
(1)若a > 0,则f ′ (x)在(-∞,w)∪(w,+∞)恒为正,
f (x)在(-∞,+∞)上递增.
(2)若a < 0,则f ′ (x)在(-∞,w)∪(w,+∞)恒为负,
f (x)在(-∞,+∞)上递减.
三次函数的单调性与极值:
情形3 函数f ′ (x)有两个零点x1和x2,如图.
(1)若a > 0,则f ′ (x)在(-∞,x1)和(x2,+∞)为正,在(x1,x2)为负,
对应地, f (x) 在(-∞,x1)上递增,在(x1,x2)上递减,在(x2,+∞)上递增.
由此可见f (x)在x = x1 处取得极大值,在x = x2 处取得极小值.
情形3 函数f ′ (x)有两个零点x = x1和x = x2,如图.
(2)若a < 0,则f ′ (x)在(-∞,x1)和(x2,+∞)为负,在(x1,x2)为正,
对应地, f (x)在(-∞,x1)上递减,在(x1,x2)上递增,在(x2,+∞)上递减.
由此可见f (x)在x = x1处取得极小值,在x = x2处取得极大值.
归 纳 总 结
三次函数的图象与性质
三次函数的单调性与极值:
设f (x)=ax3+bx2+cx+d (a≠0),则f ′ (x)=3ax2+2bx+c是二次函数.
f ′ (x)的判别式为 .
f ′ (x)的图像 f (x)的图像 f (x)的单调性 f (x)的极值
a>0 ≤0 在(-∞,+∞)上递增 无极值
>0 在(-∞,x1)上递增,在( x1 , x2 )上递减, 在(x2,+∞)上递增 极大值 f (x1)
极小值f (x2)
三次函数的单调性与极值:
设f (x)=ax3+bx2+cx+d (a≠0),则f ′ (x)=3ax2+2bx+c是二次函数.
f ′ (x)的判别式为 .
f ′ (x)的图像 f (x)的图像 f (x)的单调性 f (x)的极值
a<0 ≤0 在(-∞,+∞)上递减 无极值
>0 在(-∞,x1)上递减,在(x1,x2)上递增, 在(x2,+∞)上递减 极大值f (x2)
极小值f (x1)
谢谢!
