第十五章四边形期末单元复习题（含解析）

中小学教育资源及组卷应用平台
第十五章四边形
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，已知在锐角△ABC中，AB＝AC，AD是△ABC的角平分线，E是AD上一点，连结EB，EC．若∠EBC＝45°，BC＝6，则△EBC的面积是（ ）
A．12 B．9 C．6 D．
2．如图，要使平行四边形成为菱形，需添加的一个条件是（　　）
A． B． C． D．与互相平分
3．已知正多边形的一个外角为36°，则该正多边形的边数为( ).
A．12 B．10 C．8 D．6
4．下列说法：（1）一组对边平行，一组对角相等的四边形是平行四边形．（2）对角线相等的四边形是矩形．（3）有两条互相垂直的对称轴的四边形是菱形．（4）一条对角线平分一组对角的平行四边形是菱形．错误的个数是（ ）
A．1 B．2 C．3 D．4
5．从n边形的一个顶点出发作对角线，可以把这个n边形分成9个三角形，则n等于（ ）
A．9 B．10 C．11 D．12
6．如图，半径为10的扇形中，，C为弧AB上一点，，垂足分别为D，E．若图中阴影部分的面积为，则＝（　　）
A． B． C． D．
7．下列说法中，不正确的是（ ）
A．对角线互相平分的四边形是平行四边形
B．两组对角分别相等的四边形是平行四边形
C．一组对边平行且相等的四边形是平行四边形
D．一组对边平行另一组对边相等的四边形是平行四边形
8．若一个多边形的边数增加2倍，它的外角和( )
A．扩大2倍 B．缩小2倍 C．保持不变 D．无法确定
9．如图，在正方形外侧，以为一边向上作等边三角形，连接，则的度数是（ ）
A． B． C． D．
10．如图，在矩形中，，点和是边上的两点，连接、，将和沿、折叠后，点和点重合于点，则的长是（ ）
A．3 B．5 C．6 D．8
11．以下条件不能判别四边形ABCD是矩形的是（　　）
A．AB=CD，AD=BC，∠A=90° B．OA=OB=OC=OD
C．AB=CD，AB∥CD，AC=BD D．AB=CD，AB∥CD，OA=OC，OB=OD
12．如图，在矩形中，为的中点，F为上一动点，P为中点，连接，则的最小值是（ ）
A．2 B．4 C． D．
二、填空题
13．如图，若菱形的顶点A，B的坐标分别为，点D在y轴上，则点是 ．
14．如图，在 ABCD中，AB＝9，AD＝6，∠DAB，∠ABC的平分线AE，BF分别与直线CD交于点E，F．
（1）EF的长为 ．
（2）把“问题”中的条件“AB＝9，AD＝6”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求的值为 ．
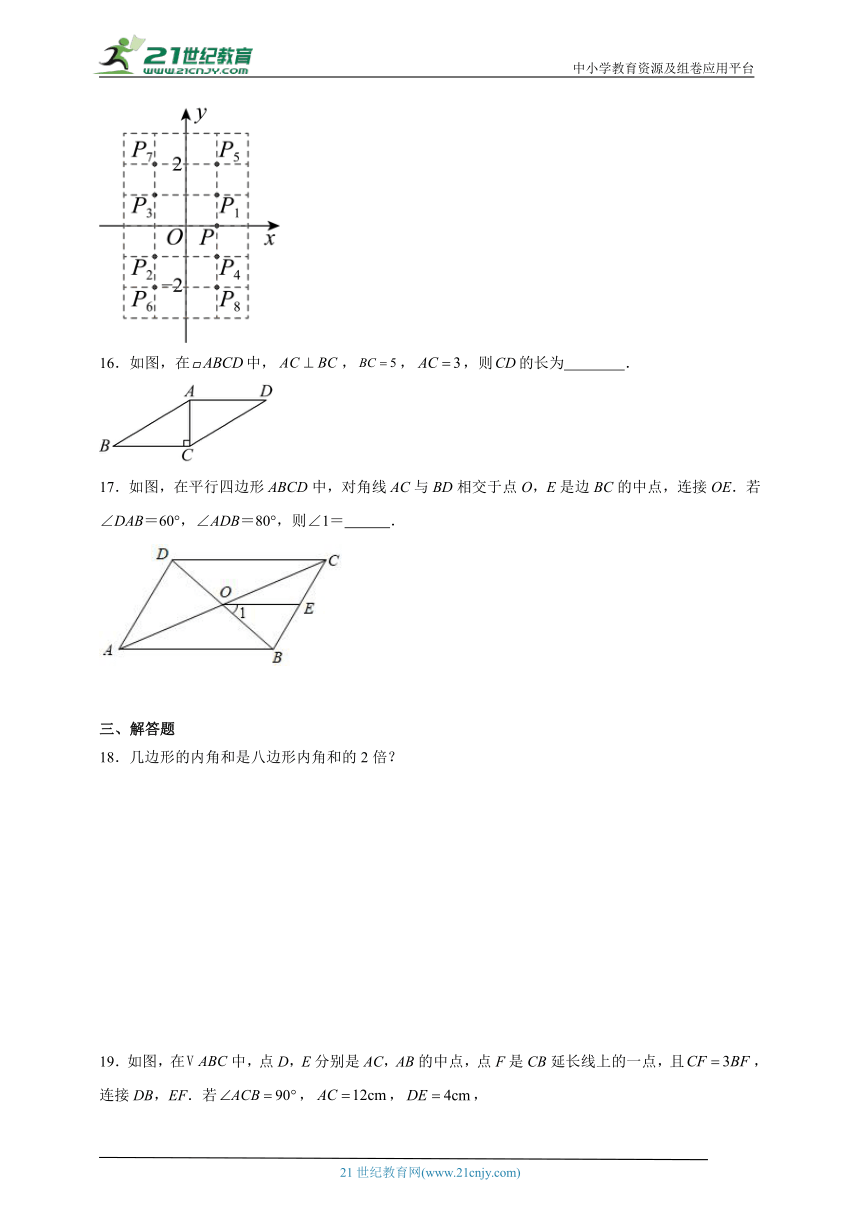
15．如图所示，在平面直角坐标系中，点作如下变换：先向上平移1个单位长度（后一次平移均比前一次多1个单位长度），再作关于原点的对称点，即将点向上平移1个单位长度得到点，作点关于原点的对称点，将点向上平移2个单位长度得到点，作点关于原点的对称点那么点的坐标是 ．

16．如图，在中，，，，则的长为 ．
17．如图，在平行四边形ABCD中，对角线AC与BD相交于点O，E是边BC的中点，连接OE．若∠DAB＝60°，∠ADB＝80°，则∠1＝ ．
三、解答题
18．几边形的内角和是八边形内角和的2倍？
19．如图，在中，点D，E分别是AC，AB的中点，点F是CB延长线上的一点，且，连接DB，EF．若，，，
(1)求证：；
(2)求四边形DEFB的周长．
20．如图，是的中线，，且，连接，．
(1)求证：；
(2)当满足条件_______时，四边形是矩形，并说明理由．
21．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
（1）试判断线段BD与CD的大小关系；
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论；
（3）若△ABC为直角三角形，且∠BAC=90°时，判断四边形AFBD的形状，并说明理由．
22．定义为函数的“特征数”．如：函数的“特征数”是，函数的“特征数”是，函数的“特征数”是
（1）将“特征数”是的函数图象向下平移2个单位，得到一个新函数，这个新函数的解析式是____________________；
（2）在（1）中，平移前后两个函数分别与y轴交于A、B两点，与直线分别交于D、C两点，判断以A、B、C、D四点为顶点的四边形的形状，说明理由并计算其周长．
23．如图，在五边形的边上，连接，可以得到几个三角形？它与边数有何关系？
24．如图，菱形ABCD中，∠B=60 ，点E在边BC上，点F在边CD上．
(1)如图1，若E是BC的中点，∠AEF=60 ，
求证：BE=DF；
(2)如图2，若∠EAF=60 ，
求证：△AEF是等边三角形．
《第十五章四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B B C B D C C C
题号 11 12
答案 D D
1．B
【分析】根据三线合一可得，根据垂直平分线的性质可得，进而根据∠EBC＝45°，可得为等腰直角三角形，根据斜边上的中线等于斜边的一半可得，然后根据三角形面积公式即可求解．
【详解】解： AB＝AC，AD是△ABC的角平分线，
，
，
∠EBC＝45°，
，
为等腰直角三角形，
，
，
则△EBC的面积是．
故选B．
【点睛】本题考查了等腰三角形的性质与判定，垂直平分线的性质，直角三角形中斜边上的中线等于斜边的一半，掌握等腰三角形的性质与判定是解题的关键．
2．A
【分析】本题主要考查了菱形的判定，根据菱形的判定方法得出A正确，B、C、D不正确；即可得出结果，熟练掌握菱形的判定：邻边相等的平行四边形是菱形；四条边都相等的四边形是菱形；对角线互相垂直的平行四边形是菱形，是解此题的关键．
【详解】解：A、四边形是平行四边形，，
平行四边形是菱形，故本选项正确；
B、四边形是平行四边形，，
平行四边形是矩形，故本选项错误；
C、四边形是平行四边形，，
四边形是矩形，
不能推出，平行四边形是菱形，故本选项错误；
D、四边形是平行四边形，
必有与互相平分，
四边形不一定是菱形；
故选：A．
3．B
【分析】利用多边形的外角和是360°，正多边形的每个外角都是36°，即可求出答案．
【详解】解：360°÷36°＝10，所以这个正多边形是正十边形．
故选B．
【点睛】本题主要考查了多边形的外角和定理．是需要识记的内容．
4．B
【分析】本题考查特殊四边形的判定方法．掌握判定特殊四边形的条件是解答本题的关键．利用平行四边形，菱形，矩形，正方形的判定条件逐项分析即可．
【详解】解：（1）根据一组对边平行，一组对角相等，结合平行线的性质，可得另一组对角也相等，即一组对边平行，一组对角相等的四边形是平行四边形，正确；
（2）对角线相等的平行四边形是矩形，故错误；
（3）有两条互相垂直的对称轴的四边形也可以是矩形，故错误；
（4）一条对角线平分一组对角的平行四边形是菱形，正确．
综上可知（2）（3）错误，有2个．
故选B．
5．C
【详解】经过n边形的一个顶点的所有对角线把多边形分成（n-2）个三角形，
依题意有n 2=9，
解得：n=11．
故选：C．
6．B
【分析】连接，得出四边形是矩形，则，得到图中阴影部分的面积＝扇形的面积，利用扇形的面积公式即可求得，然后根据平行线的性质即可求得答案．
【详解】解：连接，
∵，
∴四边形CDOE是矩形，
∴，
在与中，
，
∴，
∴图中阴影部分的面积＝扇形的面积＝，
∴，
∴，
∴，
∵，
∴，
∵，
∴，
故选：B．
【点睛】本题考查了扇形的面积，矩形的判定与性质，全等三角形的判定和性质，利用扇形的面积等于阴影的面积是解题的关键．
7．D
【分析】由平行四边形的判定方法得出A、B、C正确；即可得出结论．
【详解】解：∵对角线互相平分的四边形是平行四边形，
∴A正确；
∵两组对角分别相等的四边形是平行四边形，
∴B正确；
∵一组对边且相等的四边形是平行四边形，
∴C正确；
∵一组对边平行另一组对边相等的四边形是等腰梯形，不一定是平行四边形，
∴D不正确．
故选D．
【点睛】本题考查了平行四边形的判定方法：熟练掌握平行四边形的判定方法，并能进行推理论证是解决问题的关键．
8．C
【详解】任意多边形的外角和都是360°. 故选C.
9．C
【分析】本题考查了正方形的性质，等边三角形的性质，等腰三角形的 性质，由正方形和等边三角形的性质可得，，进而即可求解，掌握正方形和等边三角形的性质是解题的关键．
【详解】解：∵四边形是正方形，
∴，，
∵是等边三角形，
∴，，
∴，，
∴，
故选：．
10．C
【分析】本题主要考查矩形与折叠问题，等腰三角形的性质以及勾股定理等知识，过点作于点，则于点，由勾股定理可求，，设，则，由勾股定理求出，从而进一步可得出结论．
【详解】解：四边形是矩形，
，，，
由折叠得，，，，，
，
，
，
，
过点作于点，则于点，如图，则，
，
由勾股定理得，，
，
设，则，
在直角中，，
，
解得，，
，
即，
，
故选：C．
11．D
【详解】
如图：
A.∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形，
∵∠BAD=90°，
∴四边形ABCD是矩形，故本选项错误；
B.∵OA=OB=OC=OD，
∴AC=BD，
∴四边形ABCD是平行四边形，
∴四边形ABCD是矩形，故本选项错误；
C.∵AB=CD,AB∥CD，
∴四边形ABCD是平行四边形，
∵AC=BD，
∴四边形ABCD是矩形，故本选项错误；
D.∵AB∥CD，AB=CD，
∴四边形ABCD是平行四边形，
根据OA=OC，OB=OD不能推出平行四边形ABCD是矩形，故本选项正确；
故选D.
12．D
【详解】如解图，当点F与点C重合时，点P在处，，当点F与点E重合时，点P在处，且，当点F在上除点C，E的位置外时，有，由中位线定理可知：且，∴点P的运动轨迹是线段，∴当时，取得最小值，∵在矩形中，为的中点，均为等腰直角三角形，，，即的最小值为的长，在等腰直角中，，的最小值是．
13．10
【分析】利用菱形的性质以及勾股定理得出DO的长，进而三角形的面积．
【详解】解：∵菱形ABCD的顶点A，B的坐标分别为（3，0），（-2，0），点D在y轴上，
∴AB=3-（-2）=5，AB∥CD，AD=CD=AB=5，
即CD∥x轴，
在Rt△AOD中，
由勾股定理得：OD=
∴S=
故答案：10．
【点睛】此题主要考查了菱形的性质以及坐标与图形的性质，根据勾股定理求出DO的长是解题的关键．
14． 3 2或或
【分析】（1）先判定△ADE等腰三角形可得DE=AE=6,同理可得FE=BC=6,最后根据线段的和差解答即可；
（2）分点E、F在线段CD上和在CD的延长线上两种情况解答即可．
【详解】解：（1）∵在 ABCD中，AB＝9，AD＝6
∴BC=AD=6,CD=AB=9，AB//CD
∵∠DAB的平分线AE
∴∠DAE=∠EAB
∵AB//CD
∴∠DEA=∠DAB
∴∠DEA=∠DAE
∴DE=AD=6
同理：CF=BC=6
∴EF=CF+DE-CD=6+6-9=3
故答案为3．
（2）分两种情况：
①当E、F在CD上时
a.如图3：当E在F的左侧时
同（1）得：AD＝DE，
∵点C，D，E，F相邻两点间的距离相等，
∴AD＝DE＝EF＝CF，
∴AB=3DE
∴；
b.如图4：当E在F的右侧时
同（1）得：AD＝DE＝CF，
∵DF＝FE＝CE，
∴AD=2DF，AB=3DF
∴；
②如图5所示：点E、F在线段CD延长线上时
同（1）得：AD＝DE＝CF，
∵DF＝DC＝CE
∴AB=CD
∴＝2．
综上所述，的值为2或或．
【点睛】本题主要考查了平行四边形的性质、等腰三角形的性质以及分类讨论思想，灵活运用平行线四边形的性质和分类讨论思想成为解答本题的关键
15．
【分析】根据坐标变化得出规律，再判断即可．
【详解】根据题意可列出下面的表格：
向上平移 关于原点对称 向上平移 关于原点对称
… … … …
观察表格可知：这些点平均分布在四个象限中，序号除以4余1的点在第一象限，横坐标都是1，纵坐标为序号除以4的商加1；序号除以4余2的点是序号除以4余1的点关于原点的对称点；序号能被4整除的点在第四象限，横坐标为1，纵坐标为序号除以4的商的相反数；序号除以4余3的点在第二象限，是序号能被4整除的点关于原点的对称点．因为，所以点在第二象限，坐标为．
故答案为：．
【点睛】本题主要考查了坐标平面内的规律问题，掌握坐标的变化特点是解题的关键．
16．
【分析】本题考查勾股定理，平行四边形的性质．根据题意先用勾股定理求，再用平行四边形对边相等的性质即可．
【详解】解：
,
四边形是平行四边形
．
故答案为：．
17．40°
【分析】直接利用三角形内角和定理得出∠ABD的度数，再利用三角形中位线定理结合平行线的性质得出答案．
【详解】解：∵∠DAB＝60°，∠ADB＝80°，
∴∠ABD＝180°﹣60°﹣80°＝40°，
∵平行四边形ABCD对角线AC与BD相交于点O，
∴OA＝OC，
∵E是边CD的中点，
∴EO是△ABC的中位线，
∴EO∥AB，
∴∠1＝∠ABD＝40°．
故答案为：40°．
【点睛】本题考查了平行四边形的性质，三角形中位线定理，三角形内角和定理，平行线的性质，熟练掌握三角形中位线定理是解题的关键．
18．十四边形的内角和是八边形内角和的2倍.
【详解】试题分析：设n边形的内角和是八边形内角和的2倍，由题意列方程进行求解即可.
试题解析：设n边形的内角和是八边形内角和的2倍，则这个n边形内角和为：(n-2)×180°，
8边形内角和： (8-2)×180°=1080°，
∴2×1080°=2160°，
∴(n-2)×180°=2160，
∴n=14，
即十四边形的内角和是八边形内角和的2倍.
19．(1)见解析
(2)四边形DBFE的周长为28cm
【分析】（1）根据三角形中位线定理可得，根据已知条件可得即可得证；
（2）根据勾股定理求得，根据（1）的结论证明四边形DBFE是平行四边形，即可求解．
【详解】（1）证明：∵D，E分别是AC，AB的中点，
∴，，
又
即，
∴
（2），
∴，
，D是AC的中点 ，
∴，
中，
∴，
又且，
∴四边形DBFE为平行四边形．
∴四边形DBFE的周长为．
【点睛】本题考查了三角形中位线定理，平行四边形的性质与判定，勾股定理，掌握平行四边形的性质与判定以及中位线定理是解题的关键．
20．(1)见解析
(2)AB=AC或 ，见解析
【分析】（1）根据中线的性质易得，再结合得到四边形是平行四边形，最后由平行四边形的对边相等求解；
（2）先证得四边形是平行四边形，再利用△ABC是等腰三角形时四边形是矩形．
【详解】（1）解：∵是的中线，
∴．
∵，
∴．
∵，
∴四边形是平行四边形，
∴；
（2）解：当△ABC满足AB=AC或时，四边形ADCE是矩形，
∴，，
∴AE=CD．
∵AE∥BC，
∴四边形ADCE是平行四边形．
∵AB=DE，
∴当AB=AC或时，AC=DE，
∴四边形ADCE是矩形．
【点睛】本题主要考查了平行四边形的判定，等腰三角形的性质，矩形的判定，理解相关知识是解答关键．
21．（1）BD=CD；（2）矩形；（3）菱形
【详解】试题分析：（1）根据平行线的性质可得∠FAE=∠CDE，再结合∠AEF=∠DEC，AE=DE，即可证得△AEF≌△DEF，从而可以证得结论；
（2）由AF∥BC，AF=BD可证得四边形AFBD是平行四边形，再根据等腰三角形的性质可得AD⊥BC，即可证得四边形AFBD是矩形；
（3）先根据直角三角形斜边的中线是斜边的一半可证得BD=AD，再结合四边形AFBD是平行四边形可证得四边形AFBD是菱形．
（1）∵AF∥BC，
∴∠FAE=∠CDE，
∵∠AEF=∠DEC，AE=DE，
∴△AEF≌△DEF，
∴AF=CD，
∵AF=BD，
∴BD=CD；
（2）∵AF∥BC，AF=BD，
∴四边形AFBD是平行四边形，
∵AB=AC，BD=CD，
∴AD⊥BC，
∴四边形AFBD是矩形；
（3）∵∠BAC=90°，BD=CD，
∴BD=AD（直角三角形斜边的中线是斜边的一半）．
∵四边形AFBD是平行四边形，
∴四边形AFBD是菱形．
考点：平行线的性质，全等三角形的判定和性质，平行四边形、矩形、菱形的判定和性质
点评：特殊四边形的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.
22．（1）；（2）菱形，理由见解析，周长8
【分析】（1）先根据“特征数”的定义得到，“特征数”是的函数的函数解析式为，从而得到平移后的解析式为；
（2）根据（1）所求，先分别求出A、B、C、D的坐标，从而得到CD=AB=2，即可证明四边形ABCD是平行四边形，再利用勾股定理求出BC=CD=2，即可证明四边形ABCD是菱形，由此求解即可．
【详解】解：（1）∵为函数的“特征数”，
∴“特征数”是的函数的函数解析式为，
∴将函数向下平移两个单位得到的函数解析式为，
故答案为：；
（2）四边形ABCD是菱形，周长为8，理由如下：
∵A、B分别是函数、与y轴的交点，
∴，，
∴AB=2，OB=1，
∵函数、与直线分别交于D、C两点，
∴，，
∴，，
∴CD=2，OC=，
∴AB=CD，
∵A、B分别在y轴上，C、D分别在直线上，
∴AB∥CD，
∴四边形ABCD是平行四边形，
∵CD=BC=2，
∴四边形ABCD是菱形，
∴AB=BC=CD=AD=2，
∴四边形ABCD的周长=AB+BC+CD+AD=8．
【点睛】本题主要考查了一次函数的平移问题，一次函数与坐标轴的交点问题，菱形的性质与判定，平行四边形的判定，解题的关键在于能够熟练掌握相关知识机进行求解．
23．可以得到4个三角形，三角形的个数等于边数减1
【分析】根据图形找出三角形的个数，再分析出三角形个数与边数的关系即可．
【详解】解：根据图形可知，
图中共有4个三角形，三角形的个数等于边数减1．
【点睛】本题主要考查了多边形的知识，正确找出三角形的个数是解题关键．
24．(1)证明见解析；
(2)证明见解析．
【分析】（1）连接AC，由菱形ABCD中，∠B=60°，根据菱形的性质，易得△ABC是等边三角形，又由三线合一，可证得AE⊥BC，从而求得∠FEC=∠CFE，即可得EC=CF，从而证得BE=DF．
（2）连接AC，可得△ABC是等边三角形，即可得AB=AC，以求得∠ACF=∠B=60°，然后利用平行线与三角形外角的性质，可求得∠AEB=∠AFC，证得△AEB≌△AFC，即可得AE=AF，证得：△AEF是等边三角形．
【详解】（1）证明：连接AC．
∵菱形ABCD中，∠B=60°，
∴AB=BC=CD，∠C=180°－∠B=120°．
∴△ABC是等边三角形．
∵E是BC的中点，
∴AE⊥BC．
∵∠AEF=60°，
∴∠FEC=90°－∠AEF=30°．
∴∠CFE=180°－∠FEC－∠C=180°－30°－120°=30°．
∴∠FEC=∠CFE．
∴EC=CF．
∴BE=DF．
（2）证明：连接AC．
∵四边形ABCD是菱形，∠B=60°，
∴AB=BC，∠D=∠B=60°，∠ACB=∠ACF．
∴△ABC是等边三角形．
∴AB=AC，∠ACB=60°．
∴∠B=∠ACF=60°．
∵，
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD，∠AFC=∠D+∠FAD=60°+∠FAD．
∴∠AEB=∠AFC．
在△ABE和△AFC中，
∵∠B=∠ACF，∠AEB=∠AFC， AB=AC，
∴△ABE≌△ACF（AAS）．
∴AE=AF．
∵∠EAF=60°，
∴△AEF是等边三角形．
【点睛】本题考查了菱形的性质，等边三角形的判定和性质，三角形内角和定理 全等三角形的判定和性质，熟练掌握菱形的性质以及等边三角形的判定及性质是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)