第八章因式分解期末单元复习题(含解析)
文档属性
| 名称 | 第八章因式分解期末单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 600.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 17:06:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八章因式分解
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列多项式不能分解因式的是( )
A. B.20 C. D.
2.分解因式的结果为( )
A. B.
C. D.
3.下列由左边到右边的变形,属于分解因式的是( )
A. B.
C. D.
4.在日常生活中,如取款、上网等都需要密码,有一种利用“因式分解”法生成的密码,方便记忆.如:对于多项式,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“”作为一个六位数的密码.对于多项式,取,时,用上述方法生成的密码可以是( )
A. B. C. D.
5.三个多项式:,,的最大公因式是( )
A. B. C. D.
6.下列各式中能用完全平方公式进行因式分解的是( )
A. B. C. D.
7.下列各式从左到右不属于因式分解的是( )
A. B.
C. D.
8.下列多项式中,能运用平方差公式分解因式的是( )
A. B. C. D.
9.多项式2ax2 4ax 2a因式分解为( )
A.a(2x-1)2 B.a(2x+1)2 C.2a(x+1)2 D.2a(x-1)2
10.下列等式中,从左到右的变形是因式分解的是( )
A. B.
C. D.
11.下列各式中不能用平方差公式分解的是( )
A. B. C. D.
12.在多项式添加一个单项式,使得到的多项式能运用完全平方公式分解因式,则下列表述正确的是( )
嘉琪:添加,
陌陌:添加,
嘟嘟:添加,
A.嘉琪和陌陌的做法正确 B.嘉琪和嘟嘟的做法正确
C.陌陌和嘟嘟的做法正确 D.三位同学的做法都不正确
二、填空题
13.若两个多项式有公因式,则称这两个多项式为关联多项式,若与为关联多项式,则为 .
14.用完全平方公式填空: .
15.如果,则代数式的值为 .
16.因式分解: .
17.分解因式 .
三、解答题
18.下列从左到右的变形中,哪些是因式分解?哪些不是?
(1);
(2);
(3);
(4);
(5).
19.(1)若,比较与的大小,写出你的理由;
(2)若,比较与的大小,写出你的理由.
20.甲、乙两人各持一张分别写有整式A、B的卡片.已知整式,下面是甲、乙二人的对话:
甲:我的卡片上写着整式,加上整式C后得到最简整式D; 乙:我用最简整式B加上整式C后得到整式.
根据以上信息,解决下列问题:
(1)求整式D和B;
(2)请判断整式D和整式E的大小,并说明理由.
21.因式分解:
(1)
(2)
22.按要求解答下列各题:
(1)计算:;
(2)因式分解:
23.分解因式:
(1);
(2).
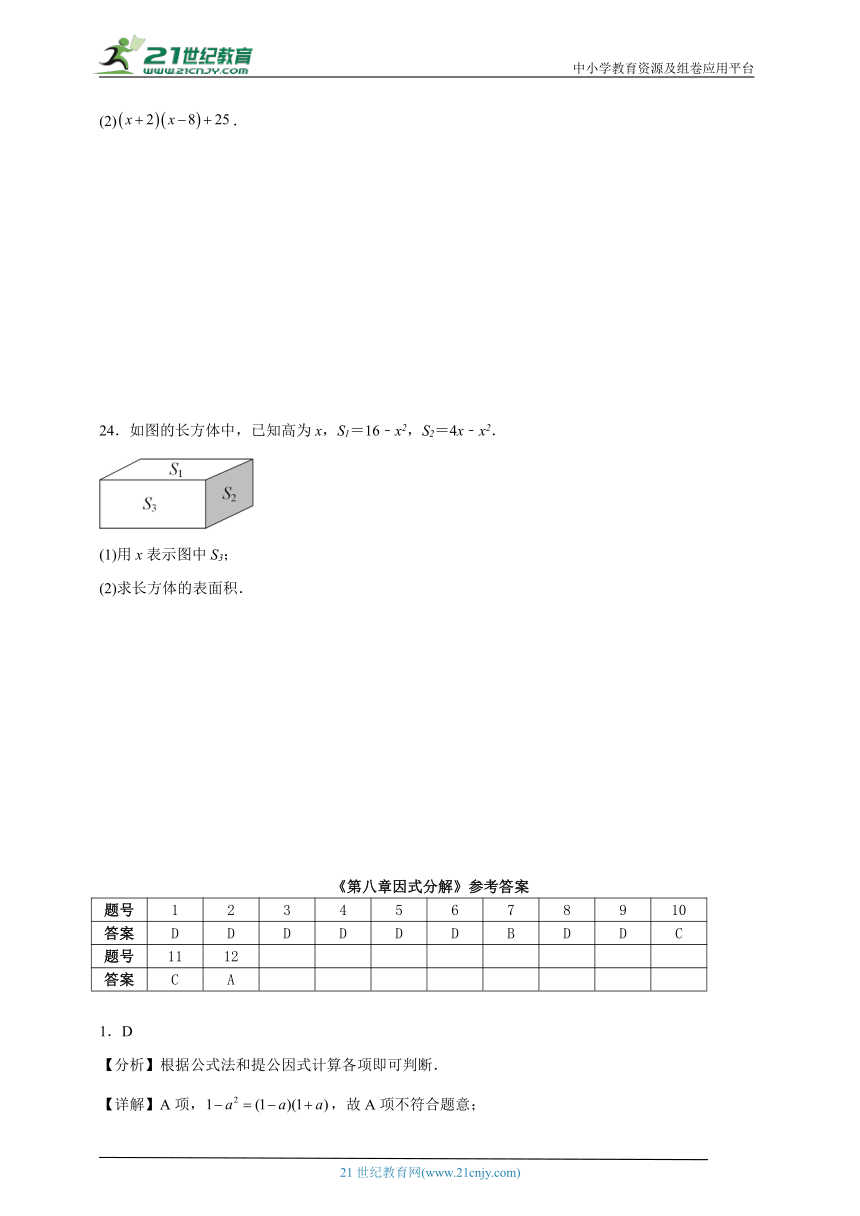
24.如图的长方体中,已知高为x,S1=16﹣x2,S2=4x﹣x2.
(1)用x表示图中S3;
(2)求长方体的表面积.
《第八章因式分解》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D D D D B D D C
题号 11 12
答案 C A
1.D
【分析】根据公式法和提公因式计算各项即可判断.
【详解】A项,,故A项不符合题意;
B项,20是是一个数,而不是多项式,故B项不合题意;
C项,,故C项不符合题意;
D项,无法进行因式分解,故D项符合题意;
故选:D.
【点睛】本题考查了多项式的定义以及用提公因式法和公式法进行因式分解的知识,掌握因式分解的方法是解答本题的关键.几个单项式的和是多项式.
2.D
【分析】根据平方差公式因式分解即可求解,注意分解要彻底.
【详解】解:原式=,
故选D
【点睛】本题考查了平方差公式因式分解,掌握平方差公式是解题的关键.
3.D
【分析】根据因式分解的定义逐项分析判断即可求解.
【详解】解:A. ,不是因式分解,故该选项不正确,不符合题意;
B. ,是整式乘法,不是因式分解,故该选项不正确,不符合题意;
C. ,不是多项式的乘积的形式,不是因式分解,故该选项不正确,不符合题意;
D. ,属于因式分解,故该选项正确,符合题意;
故选:D.
【点睛】本题考查了因式分解的定义,解题的关键是熟练掌握因式分解的定义:把一个多项式化为几个最简整式的积的形式,这种变形叫做把这个多项式因式分解.
4.D
【分析】首先对多项式提公因式,再利用平方差公式分解因式,然后把数值代入计算,即可确定出密码.
【详解】解:
,
当,时,,,,
∴上述方法生成的密码可以是.
故选:D
【点睛】本题考查了因式分解的应用,涉及分解因式的方法有:提公因式法,以及平方差公式法,属于阅读型的新定义题,其中根据阅读材料得出产生密码的方法是解本题的关键.
5.D
【分析】先把三个多项式因式分解,再进行解答即可.
【详解】解:∵,,,
∴最大公因式是.
故选D.
【点睛】本题主要考查了最大公因式,熟练掌握最大公因式的定义,将三个多项式分解因式,是解题的关键.
6.D
【分析】能用完全平方公式分解的式子的特点是:三项;两项平方项的符号需相同;有一项是两平方项底数积的2倍,据此逐项分析即可.
【详解】A.不能用完全平方公式因式分解,故不符合题意;
B.不能用完全平方公式因式分解,故不符合题意;
C.不能用完全平方公式因式分解,故不符合题意;
D.,符合题意,
故选:D.
【点睛】本题考查了完全平方公式进行因式分解,熟练掌握是解答本题的关键.两个平方项的符号需相同;另一项是两底数积的2倍,是易错点.
7.B
【分析】根据因式分解的意义逐个判断即可.
【详解】解:A.属于因式分解,不符合题意;
B.右边不是几个整式积的形式,不属于因式分解,符合题意;
C.属于因式分解,不符合题意;
D.属于因式分解,不符合题意.
故选:B.
【点睛】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式.
8.D
【分析】利用平方差公式的结构特征判断即可.
【详解】解:能运用平方差公式分解因式的是:.
故选:D.
【点睛】此题考查了平方差公式的综合运用,熟练掌握平方差公式是解本题的关键.
9.D
【分析】提取公因式2a后,再运用公式法分解即可.
【详解】解:2ax2 4ax 2a
故选:D
【点睛】此题主要考查了提取公因式法和运用公式法分解因式,正确找出公因式是解题关键.
10.C
【详解】根据因式分解的定义(把一个多项式化成几个最简整式的乘积的形式,这种多项式的变形叫做因式分解)逐项判断即可得.
【解答】解:A、是整式的乘法,不是因式分解,故此选项不符合题意;
B、是整式的乘法,不是因式分解,故此选项不符合题意;
C、把一个多项式转化成几个整式乘积的形式,是因式分解,故此选项符合题意;
D、等式右边中的不是整式,不是因式分解,故此选项不符合题意.
故选:C.
【点睛】本题考查了因式分解的意义;严格按照因式分解的定义去验证每个选项是正确解答本题的关键.
11.C
【分析】此题考查了因式分解运用公式法,熟练掌握平方差公式是解本题的关键.
利用平方差公式的结构特征判断即可.
【详解】A.,具备平方差公式的结构特征,故此多项式能用平方差公式分解,不符合题意;
B.,具备平方差公式的结构特征,故此多项式能用平方差公式分解,不符合题意;
C.,不具备平方差公式的结构特征,故此多项式不能用平方差公式分解,符合题意;
D.,具备平方差公式的结构特征,故此多项式能用平方差公式分解,不符合题意.
故选:C.
12.A
【分析】利用完全平方公式分解即可.
【详解】解:添加,,故嘉琪的表述是正确的;
添加,,故陌陌的表述是正确的;
嘟嘟的表述不是完全平方公式,故是错误的.
故选:A.
【点睛】本题考查因式分解—公式法.熟练掌握因式分解的方法是解题的关键.
13.
【分析】将多项式因式分解,根据公因式的定义即可得出答案.
【详解】解:根据题意,则
=(x+5)(x5),
∵与为关联多项式,
∴b=±5.
故答案为:±5.
【点睛】本题考查了公因式,掌握多项式ma+mb+mc中,各项都含有一个公共的因式m,因式m叫做这个多项式各项的公因式是解题的关键.
14.
【分析】运用完全平方公式,结合“整体”思想.
【详解】解:;
故答案为:.
【点睛】本题考查完全平方公式;掌握完全平方公式的特征是解题的关键.
15.
【分析】把代数式变形整理成的形式,再运用整体代入法求解.
【详解】解:,
,
,
,
,
,
.
故答案为:.
【点睛】本题考查了提公因式法分解因式,对前两项提取公因式是解题的关键,然后利用“整体代入法”求代数式的值.
16.
【分析】本题主要考查了因式分解,解题的关键是熟练掌握完全平方公式,将看作一个整体,根据完全平方公式,分解因式即可.
【详解】解:.
故答案为:.
17.
【分析】前三项一个组合,用完全平方公式分解因式,再用平方差公式分解因式即可解答;
【详解】
=
=(a+2b+1)(a+2b-1)
故答案为:(a+2b+1)(a+2b-1).
【点睛】本题考查了公式法分解因式,本题先用完全平方公式,再用平方差公式,注意分解因式一定要彻底.
18.(1)不是因式分解
(2)不是因式分解
(3)是因式分解
(4)不是因式分解
(5)不是因式分解
【分析】本题考查了因式分解的意义,注意因式分解是针对多项式而言的,因式分解后,右边是整式积的形式.
根据分解因式的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式
【详解】(1)解:因式分解是针对多项式来说的,故不是因式分解;
(2)解:等号右边不是整式积的形式,不是因式分解;
(3)解:是因式分解;
(4)解:等号右边不是整式积的形式,不是因式分解;
(5)解:等号右边不是整式积的形式,不是因式分解.
19.(1),见解析;(2),见解析
【分析】本题考查了不等式性质的应用,因式分解的应用,熟练掌握相关知识是解题的关键.
(1)由不等式的性质,两边同时乘以得,两边同时加1得;
(2)利用平方差公式因式分解和不等式的性质即可解答.
【详解】解:(1),理由如下:
,
,
;
(2)∵,,
∴,
∴,
∴,
∴.
20.(1)
(2),理由见解析
【分析】(1)根据题意得:D=A+C,B=E-C,把各自的整式代入,去括号合并即可得到结果;
(2)利用作差法判断D与E的大小即可.
【详解】(1)解:∵,,
∴D=A+C
,
B=E-C
,
∴;
(2),理由如下:
∵
>0
【点睛】此题考查了整式的加减,运用完全平方公式因式分解,熟练掌握去括号法则与合并同类项法则是解本题的关键.
21.(1)
(2)
【分析】(1)先提公因式,然后根据平方差公式进行计算即可求解;
(2)先根据完全平方公式展开,然后根据完全平方公式与平方差公式因式分解即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了因式分解,掌握因式分解的方法以及乘法公式是解题的关键.
22.(1)
(2)
【分析】(1)利用平方差公式和多项式除以单项式法则计算,再合并;
(2)先提公因式,再利用平方差公式分解即可.
【详解】(1)解:
;
(2)
【点睛】本题考查了整式的混合运算,因式分解,解题的关键是掌握运算法则和因式分解的步骤.
23.(1)
(2)
【分析】(1)利用完全平方公式进行因式分解即可;
(2)先根据多项式乘多项式的法则,展开,再利用完全平方公式进行因式分解.
【详解】(1)解:原式
;
(2)原式
.
【点睛】本题考查因式分解.熟练掌握因式分解的方法,是解题的关键.
24.(1)S3=4x+x2
(2)-2x2+16x+32
【分析】(1)分别表示长方体的长和宽,可得S3;
(2)根据表面积公式代入可得答案.
【详解】(1)∵S2=4x x2=x(4 x),
∴长方体的宽=4-x,
∵S1=16 x2=(4 x)(4+x)
∴长方体的长=4+x,
∴S3=x(4+x)=4x+x2;
(2)长方体的表面积=2(4x+x2)+2(16-x2)+2(4x-x2)
=8x+2x2+32-2x2+8x-2x2
=-2x2+16x+32.
【点睛】本题考查了长方体,整式的加减,以及因式分解的应用,掌握长方形的面积=长×宽是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章因式分解
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列多项式不能分解因式的是( )
A. B.20 C. D.
2.分解因式的结果为( )
A. B.
C. D.
3.下列由左边到右边的变形,属于分解因式的是( )
A. B.
C. D.
4.在日常生活中,如取款、上网等都需要密码,有一种利用“因式分解”法生成的密码,方便记忆.如:对于多项式,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“”作为一个六位数的密码.对于多项式,取,时,用上述方法生成的密码可以是( )
A. B. C. D.
5.三个多项式:,,的最大公因式是( )
A. B. C. D.
6.下列各式中能用完全平方公式进行因式分解的是( )
A. B. C. D.
7.下列各式从左到右不属于因式分解的是( )
A. B.
C. D.
8.下列多项式中,能运用平方差公式分解因式的是( )
A. B. C. D.
9.多项式2ax2 4ax 2a因式分解为( )
A.a(2x-1)2 B.a(2x+1)2 C.2a(x+1)2 D.2a(x-1)2
10.下列等式中,从左到右的变形是因式分解的是( )
A. B.
C. D.
11.下列各式中不能用平方差公式分解的是( )
A. B. C. D.
12.在多项式添加一个单项式,使得到的多项式能运用完全平方公式分解因式,则下列表述正确的是( )
嘉琪:添加,
陌陌:添加,
嘟嘟:添加,
A.嘉琪和陌陌的做法正确 B.嘉琪和嘟嘟的做法正确
C.陌陌和嘟嘟的做法正确 D.三位同学的做法都不正确
二、填空题
13.若两个多项式有公因式,则称这两个多项式为关联多项式,若与为关联多项式,则为 .
14.用完全平方公式填空: .
15.如果,则代数式的值为 .
16.因式分解: .
17.分解因式 .
三、解答题
18.下列从左到右的变形中,哪些是因式分解?哪些不是?
(1);
(2);
(3);
(4);
(5).
19.(1)若,比较与的大小,写出你的理由;
(2)若,比较与的大小,写出你的理由.
20.甲、乙两人各持一张分别写有整式A、B的卡片.已知整式,下面是甲、乙二人的对话:
甲:我的卡片上写着整式,加上整式C后得到最简整式D; 乙:我用最简整式B加上整式C后得到整式.
根据以上信息,解决下列问题:
(1)求整式D和B;
(2)请判断整式D和整式E的大小,并说明理由.
21.因式分解:
(1)
(2)
22.按要求解答下列各题:
(1)计算:;
(2)因式分解:
23.分解因式:
(1);
(2).
24.如图的长方体中,已知高为x,S1=16﹣x2,S2=4x﹣x2.
(1)用x表示图中S3;
(2)求长方体的表面积.
《第八章因式分解》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D D D D B D D C
题号 11 12
答案 C A
1.D
【分析】根据公式法和提公因式计算各项即可判断.
【详解】A项,,故A项不符合题意;
B项,20是是一个数,而不是多项式,故B项不合题意;
C项,,故C项不符合题意;
D项,无法进行因式分解,故D项符合题意;
故选:D.
【点睛】本题考查了多项式的定义以及用提公因式法和公式法进行因式分解的知识,掌握因式分解的方法是解答本题的关键.几个单项式的和是多项式.
2.D
【分析】根据平方差公式因式分解即可求解,注意分解要彻底.
【详解】解:原式=,
故选D
【点睛】本题考查了平方差公式因式分解,掌握平方差公式是解题的关键.
3.D
【分析】根据因式分解的定义逐项分析判断即可求解.
【详解】解:A. ,不是因式分解,故该选项不正确,不符合题意;
B. ,是整式乘法,不是因式分解,故该选项不正确,不符合题意;
C. ,不是多项式的乘积的形式,不是因式分解,故该选项不正确,不符合题意;
D. ,属于因式分解,故该选项正确,符合题意;
故选:D.
【点睛】本题考查了因式分解的定义,解题的关键是熟练掌握因式分解的定义:把一个多项式化为几个最简整式的积的形式,这种变形叫做把这个多项式因式分解.
4.D
【分析】首先对多项式提公因式,再利用平方差公式分解因式,然后把数值代入计算,即可确定出密码.
【详解】解:
,
当,时,,,,
∴上述方法生成的密码可以是.
故选:D
【点睛】本题考查了因式分解的应用,涉及分解因式的方法有:提公因式法,以及平方差公式法,属于阅读型的新定义题,其中根据阅读材料得出产生密码的方法是解本题的关键.
5.D
【分析】先把三个多项式因式分解,再进行解答即可.
【详解】解:∵,,,
∴最大公因式是.
故选D.
【点睛】本题主要考查了最大公因式,熟练掌握最大公因式的定义,将三个多项式分解因式,是解题的关键.
6.D
【分析】能用完全平方公式分解的式子的特点是:三项;两项平方项的符号需相同;有一项是两平方项底数积的2倍,据此逐项分析即可.
【详解】A.不能用完全平方公式因式分解,故不符合题意;
B.不能用完全平方公式因式分解,故不符合题意;
C.不能用完全平方公式因式分解,故不符合题意;
D.,符合题意,
故选:D.
【点睛】本题考查了完全平方公式进行因式分解,熟练掌握是解答本题的关键.两个平方项的符号需相同;另一项是两底数积的2倍,是易错点.
7.B
【分析】根据因式分解的意义逐个判断即可.
【详解】解:A.属于因式分解,不符合题意;
B.右边不是几个整式积的形式,不属于因式分解,符合题意;
C.属于因式分解,不符合题意;
D.属于因式分解,不符合题意.
故选:B.
【点睛】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式.
8.D
【分析】利用平方差公式的结构特征判断即可.
【详解】解:能运用平方差公式分解因式的是:.
故选:D.
【点睛】此题考查了平方差公式的综合运用,熟练掌握平方差公式是解本题的关键.
9.D
【分析】提取公因式2a后,再运用公式法分解即可.
【详解】解:2ax2 4ax 2a
故选:D
【点睛】此题主要考查了提取公因式法和运用公式法分解因式,正确找出公因式是解题关键.
10.C
【详解】根据因式分解的定义(把一个多项式化成几个最简整式的乘积的形式,这种多项式的变形叫做因式分解)逐项判断即可得.
【解答】解:A、是整式的乘法,不是因式分解,故此选项不符合题意;
B、是整式的乘法,不是因式分解,故此选项不符合题意;
C、把一个多项式转化成几个整式乘积的形式,是因式分解,故此选项符合题意;
D、等式右边中的不是整式,不是因式分解,故此选项不符合题意.
故选:C.
【点睛】本题考查了因式分解的意义;严格按照因式分解的定义去验证每个选项是正确解答本题的关键.
11.C
【分析】此题考查了因式分解运用公式法,熟练掌握平方差公式是解本题的关键.
利用平方差公式的结构特征判断即可.
【详解】A.,具备平方差公式的结构特征,故此多项式能用平方差公式分解,不符合题意;
B.,具备平方差公式的结构特征,故此多项式能用平方差公式分解,不符合题意;
C.,不具备平方差公式的结构特征,故此多项式不能用平方差公式分解,符合题意;
D.,具备平方差公式的结构特征,故此多项式能用平方差公式分解,不符合题意.
故选:C.
12.A
【分析】利用完全平方公式分解即可.
【详解】解:添加,,故嘉琪的表述是正确的;
添加,,故陌陌的表述是正确的;
嘟嘟的表述不是完全平方公式,故是错误的.
故选:A.
【点睛】本题考查因式分解—公式法.熟练掌握因式分解的方法是解题的关键.
13.
【分析】将多项式因式分解,根据公因式的定义即可得出答案.
【详解】解:根据题意,则
=(x+5)(x5),
∵与为关联多项式,
∴b=±5.
故答案为:±5.
【点睛】本题考查了公因式,掌握多项式ma+mb+mc中,各项都含有一个公共的因式m,因式m叫做这个多项式各项的公因式是解题的关键.
14.
【分析】运用完全平方公式,结合“整体”思想.
【详解】解:;
故答案为:.
【点睛】本题考查完全平方公式;掌握完全平方公式的特征是解题的关键.
15.
【分析】把代数式变形整理成的形式,再运用整体代入法求解.
【详解】解:,
,
,
,
,
,
.
故答案为:.
【点睛】本题考查了提公因式法分解因式,对前两项提取公因式是解题的关键,然后利用“整体代入法”求代数式的值.
16.
【分析】本题主要考查了因式分解,解题的关键是熟练掌握完全平方公式,将看作一个整体,根据完全平方公式,分解因式即可.
【详解】解:.
故答案为:.
17.
【分析】前三项一个组合,用完全平方公式分解因式,再用平方差公式分解因式即可解答;
【详解】
=
=(a+2b+1)(a+2b-1)
故答案为:(a+2b+1)(a+2b-1).
【点睛】本题考查了公式法分解因式,本题先用完全平方公式,再用平方差公式,注意分解因式一定要彻底.
18.(1)不是因式分解
(2)不是因式分解
(3)是因式分解
(4)不是因式分解
(5)不是因式分解
【分析】本题考查了因式分解的意义,注意因式分解是针对多项式而言的,因式分解后,右边是整式积的形式.
根据分解因式的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式
【详解】(1)解:因式分解是针对多项式来说的,故不是因式分解;
(2)解:等号右边不是整式积的形式,不是因式分解;
(3)解:是因式分解;
(4)解:等号右边不是整式积的形式,不是因式分解;
(5)解:等号右边不是整式积的形式,不是因式分解.
19.(1),见解析;(2),见解析
【分析】本题考查了不等式性质的应用,因式分解的应用,熟练掌握相关知识是解题的关键.
(1)由不等式的性质,两边同时乘以得,两边同时加1得;
(2)利用平方差公式因式分解和不等式的性质即可解答.
【详解】解:(1),理由如下:
,
,
;
(2)∵,,
∴,
∴,
∴,
∴.
20.(1)
(2),理由见解析
【分析】(1)根据题意得:D=A+C,B=E-C,把各自的整式代入,去括号合并即可得到结果;
(2)利用作差法判断D与E的大小即可.
【详解】(1)解:∵,,
∴D=A+C
,
B=E-C
,
∴;
(2),理由如下:
∵
>0
【点睛】此题考查了整式的加减,运用完全平方公式因式分解,熟练掌握去括号法则与合并同类项法则是解本题的关键.
21.(1)
(2)
【分析】(1)先提公因式,然后根据平方差公式进行计算即可求解;
(2)先根据完全平方公式展开,然后根据完全平方公式与平方差公式因式分解即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了因式分解,掌握因式分解的方法以及乘法公式是解题的关键.
22.(1)
(2)
【分析】(1)利用平方差公式和多项式除以单项式法则计算,再合并;
(2)先提公因式,再利用平方差公式分解即可.
【详解】(1)解:
;
(2)
【点睛】本题考查了整式的混合运算,因式分解,解题的关键是掌握运算法则和因式分解的步骤.
23.(1)
(2)
【分析】(1)利用完全平方公式进行因式分解即可;
(2)先根据多项式乘多项式的法则,展开,再利用完全平方公式进行因式分解.
【详解】(1)解:原式
;
(2)原式
.
【点睛】本题考查因式分解.熟练掌握因式分解的方法,是解题的关键.
24.(1)S3=4x+x2
(2)-2x2+16x+32
【分析】(1)分别表示长方体的长和宽,可得S3;
(2)根据表面积公式代入可得答案.
【详解】(1)∵S2=4x x2=x(4 x),
∴长方体的宽=4-x,
∵S1=16 x2=(4 x)(4+x)
∴长方体的长=4+x,
∴S3=x(4+x)=4x+x2;
(2)长方体的表面积=2(4x+x2)+2(16-x2)+2(4x-x2)
=8x+2x2+32-2x2+8x-2x2
=-2x2+16x+32.
【点睛】本题考查了长方体,整式的加减,以及因式分解的应用,掌握长方形的面积=长×宽是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
