第二单元折线统计图期末复习练(含解析)苏教版数学五年级下册
文档属性
| 名称 | 第二单元折线统计图期末复习练(含解析)苏教版数学五年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 809.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二单元折线统计图
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.要反映商场不同品牌空调的销售量情况,选择( )比较合适.
A.条形统计图 B.折线统计图
C.两种都可以
2.要反映本次考试优、良、中、差各段学生人数,应该绘制( )。
A.折线统计图 B.条形统计图 C.统计表
3.从一个城市的一周气温情况折线统计图中,不能看出( ).
A.这周气温变化趋势 B.这周哪天气温最高
C.气温变化的原因
4.星期天,小明的爸爸去了一趟相距15千米的老家看望奶奶。他出行的路程和时间的关系如图所示,下面对他的出行方式描述正确的是( )。
A.去时骑自行车,返回时乘公共汽车 B.去时骑自行车,返回时步行
C.去时步行,返回时乘公共汽车 D.去时乘公共汽车,返回时骑自行车
5.要了解小丽在六年级全年的数学成绩变化,选择( )较合适。
A.条形统计图 B.折线统计图 C.扇形统计图
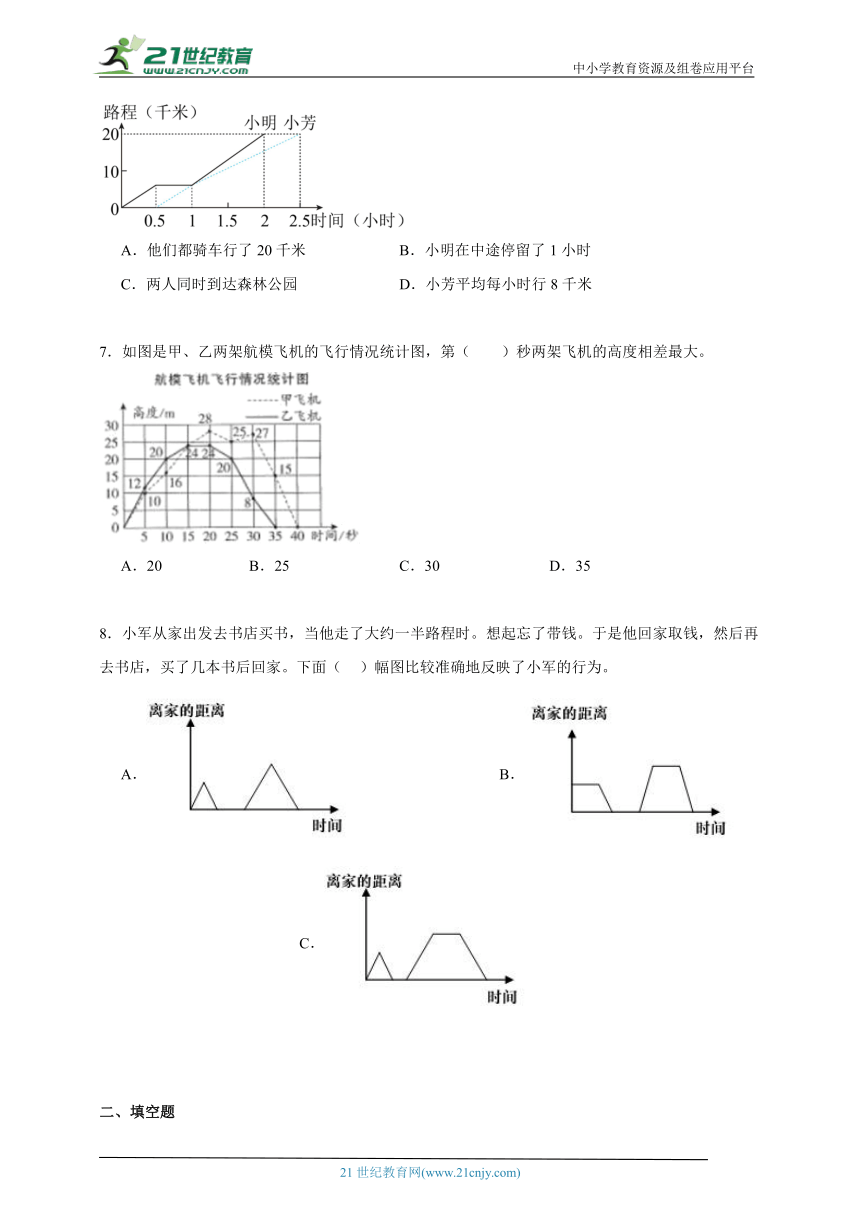
6.小明和小芳骑车从学校沿同一路线到20千米外的公园,已知小明比小芳先出发,他俩所行的路程与时间的关系如图所示。下面说法正确的是( )。
A.他们都骑车行了20千米 B.小明在中途停留了1小时
C.两人同时到达森林公园 D.小芳平均每小时行8千米
7.如图是甲、乙两架航模飞机的飞行情况统计图,第( )秒两架飞机的高度相差最大。
A.20 B.25 C.30 D.35
8.小军从家出发去书店买书,当他走了大约一半路程时。想起忘了带钱。于是他回家取钱,然后再去书店,买了几本书后回家。下面( )幅图比较准确地反映了小军的行为。
A. B. C.
二、填空题
9.统计一周内日平均气温的变化情况,应选择 统计图。
10.折线统计图有 和 两种。
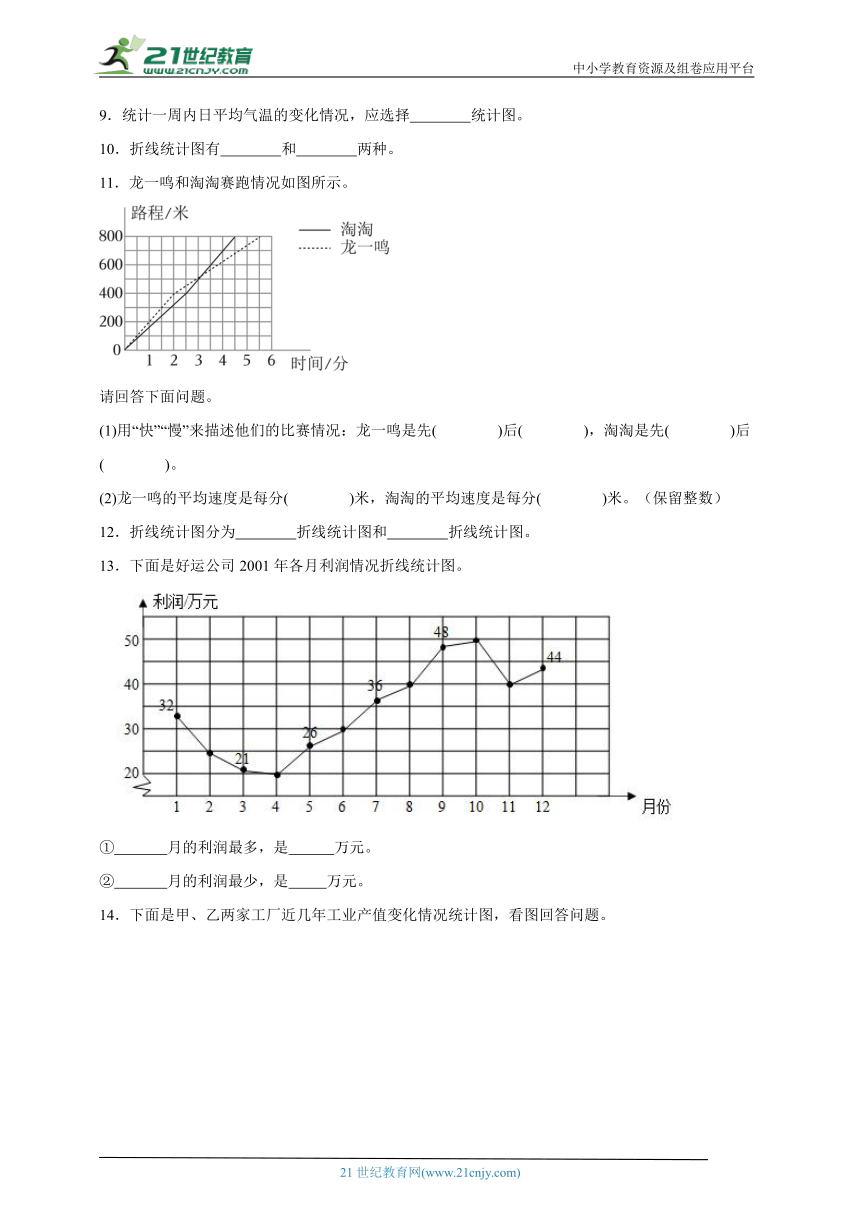
11.龙一鸣和淘淘赛跑情况如图所示。
请回答下面问题。
(1)用“快”“慢”来描述他们的比赛情况:龙一鸣是先( )后( ),淘淘是先( )后( )。
(2)龙一鸣的平均速度是每分( )米,淘淘的平均速度是每分( )米。(保留整数)
12.折线统计图分为 折线统计图和 折线统计图。
13.下面是好运公司2001年各月利润情况折线统计图。
① 月的利润最多,是 万元。
② 月的利润最少,是 万元。
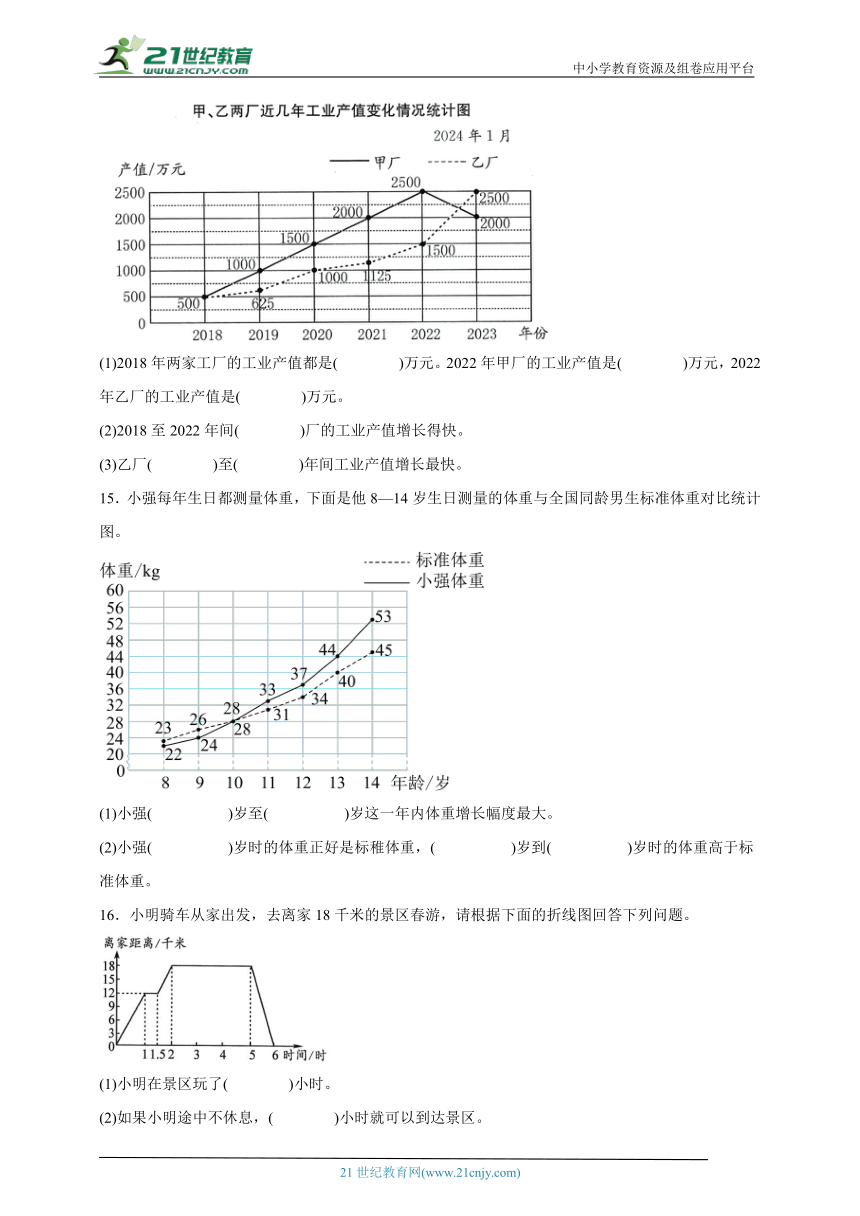
14.下面是甲、乙两家工厂近几年工业产值变化情况统计图,看图回答问题。
(1)2018年两家工厂的工业产值都是( )万元。2022年甲厂的工业产值是( )万元,2022年乙厂的工业产值是( )万元。
(2)2018至2022年间( )厂的工业产值增长得快。
(3)乙厂( )至( )年间工业产值增长最快。
15.小强每年生日都测量体重,下面是他8—14岁生日测量的体重与全国同龄男生标准体重对比统计图。
(1)小强( )岁至( )岁这一年内体重增长幅度最大。
(2)小强( )岁时的体重正好是标稚体重,( )岁到( )岁时的体重高于标准体重。
16.小明骑车从家出发,去离家18千米的景区春游,请根据下面的折线图回答下列问题。
(1)小明在景区玩了( )小时。
(2)如果小明途中不休息,( )小时就可以到达景区。
(3)小明返回时每小时行( )千米。
三、判断题
17.任意两个折线统计图都可以合成一个复式折线统计图。( )
18.在复式折线统计图中,两条折线相交的点表示数量相等。( )
19.要记录6月份每天的气温变化情况,选用折线统计图最合适。( )
20.折线统计图易看出数量的多少,条形统计图易看出数量的增减变化情况。( )
四、计算题
21.解方程。
五、解答题
22.在我国的南方和北方各选一座城市,了解这两座城市去年每月的降水量,完成下面的统计图。
根据图中的数据,你能得出什么结论?
23.甲市和乙市某天6~22时的气温变化情况如图所示。
(1)纵轴上每个单位长度表示( )℃。
(2)甲市和乙市这一天( )时气温相差最大,( )时气温相差最小。
(3)根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是( )℃。
24.小刚和小强赛跑情况如下图
(1)________先到达终点。
(2)请用“快”、“慢”来描述他们的比赛情况:小刚是________后________
(3)开赛初________领先,开赛________分后________领先,比赛中两人相距最远约是________米。
(4)两人的平均速度分别是每分多少米?(保留整数)
25.看统计图回答问题。
(1)九月销量比八月下降百分之几?
(2)每件游泳衣售价30元,按8%的税率缴纳营业税,商店五个月营业额的税后收入是多少元?
《第二单元折线统计图》参考答案
题号 1 2 3 4 5 6 7 8
答案 A B C D B A C C
1.A
【详解】略
2.B
【详解】因为条形统计图能很容易看出数量的多少,所以要反映本次考试优、良、中、差各段学生人数,应该绘制条形统计图。条形统计图能很容易看出数量的多少,关键是掌握条形统计图的特点。
故答案为:B
3.C
【详解】略
4.D
【分析】由路程、速度和时间三者之间的关系可知,速度=路程÷时间。根据题意可知,步行速度应小于骑自行车速度小于乘公共汽车的速度。在图中,当横轴代表时间,纵轴代表路程时,线段越陡,速度越快。据此解答。
【详解】小明家与奶奶家的距离为15千米,距离较远应骑自行车或乘公共汽车。
读图可知:
第一段线段,表示从家去奶奶家,所用时间较少,速度较快,应乘公共汽车;
第二段线段,表示在奶奶家停留,距离不发生变化;
第三段线段,表示从奶奶家返回,所用时间较长,速度较慢,应骑自行车;
所以,去时乘公共汽车,返回时骑自行车。
故答案为:D
5.B
【分析】条形统计图能直观反映出数据的多少,折线统计图不仅能反映数据的多少,还能体现出数据增减变化趋势,扇形统计图能反映出部分与整体之间的数量关系,据此即可得出答案。
【详解】要了解小丽在六年级全年的数学成绩变化,即要选择能反映数据增减变化趋势的统计图,则折线统计图较合适。
故答案为:B
6.A
【分析】A.观察复式折线统计图,数轴表示路程,小明和小芳数据点最高的位置表示总路程;
B.折线往上表示正在骑行,折线平缓无变化,表示中途停留,根据终点时间-起点时间=经过时间,计算出停留时间;
C.实线表示小明数据,虚线表示小芳数据,小明2小时到达公园,小芳2.5小时到达公园,据此分析;
D.先计算出小芳骑行时间,根据路程÷时间=速度,列式计算即可。
【详解】A.他们都骑车行了20千米,说法正确;
B.小明在中途停留了0.5小时,选项说法错误;
C.小明比小芳先到达森林公园,选项说法错误;
D.20÷(2.5-0.5)
=20÷2
=10(千米)
小芳平均每小时行10千米,选项说法错误。
说法正确的是他们都骑车行了20千米。
故答案为:A
7.C
【详解】在第30秒两架飞机的高度相差最大,相差27﹣8=19(米)。
故选:C.
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
8.C
【分析】离家的距离是随时间是这样变化的:
(1)先离家越来越远,到了最远距离一半的时候;(2)然后越来越近直到为0;(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;(4)然后再离家越来越远,直到书店;(5)在书店买书还要一段时间,所以离家最远的时候也是一条水平线段;(6)然后回家直到离家的距离为0。
【详解】符合小军这段时间离家距离变化的是C。
故选: C
【点睛】本题需要考虑到在家和在书店都有一段时间离家的距离不会变化。
9.折线
【详解】略
10. 单式折线统计图; 复式折线统计图
【详解】单式折线统计图只表示一种量,复式折线统计图表示两种或两种以上的量。
11.(1) 快 慢 慢 快
(2) 145 178
【分析】(1)实线表示淘淘,虚线表示龙一鸣,根据折线统计图可知,在400米时,淘淘用了2.5分钟,龙一鸣用了2分钟,到达终点时,淘淘用了4.5分钟,龙一鸣用了5.5分钟,所以龙一鸣的比赛情况是先快后慢;淘淘是先慢后快,据此解答即可;
(2)可根据路程÷时间=速度进行计算即可得到答案。
【详解】(1)龙一鸣先快后慢,淘淘是先慢后快。
(2)800÷5.5≈145(米/分)
800÷4.5≈178(米/分)
即龙一鸣的平均速度是145米/分,淘淘的平均速度是178米/分。
【点睛】此题主要考查的是如何从折线统计图中获取信息,然后再分析计算即可。
12. 单式 复式
【详解】以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图,折线统计图可以分为单式折线统计和复式折线统计图两种。
13. 10 50 4 20
【分析】从折线图中可以直接看出和读出数据。
【详解】横轴表示的是月份,纵轴表示的是利润,所以从图中可以直接出,10月的利润最多,是50万元;4月的利润最少,是20万元。
14.(1) 500 2500 1500
(2)甲
(3) 2022 2023
【分析】(1)观察统计图中折线的走势和对应的数据点来回答问题;先从统计图中读取特定年份的产值数据回答:
(2)分别计算甲、乙两厂在2018-2022年间的产值增长量,再比较大小;
(3)最后计算乙厂各相邻年份间的产值增长量,找出增长最快的时间段。
【详解】(1)观察统计图可知,在2018年这个时间点,甲厂和乙厂对应的产值都是500万元。
在统计图中,2022年甲厂对应的产值是2500万元,2022年乙厂对应的产值是1500万元。
(2)2500-500=2000(万元)
1500-500=1000(万元)
2000>1000
所以2018至2022年间甲厂的工业产值增长得快。
(3)2018-2019年乙厂产值为625万元,2018年为500万元,增长量:625-500=125(万元)。
计算乙厂2019-2020年间的产值增长量:2020年乙厂产值为1000万元,2019年为625万元,增长量=1000-625=375(万元)。
计算乙厂2020-2021年间的产值增长量:2021年乙厂产值为1125万元,2020年为1000万元,增长量=1125-1000=125(万元)。
计算乙厂2021-2022年间的产值增长量:2022年乙厂产值为1500万元,2021年为1125万元,增长量=1500-1125 = 375(万元)。
计算乙厂2022-2023年间的产值增长量:2022年乙厂产值为1500万元,2023年为2500万元,增长量:2500-1500=1000(万元)
比较各时间段的增长量125<375<1000,可知:2022-2023年间增长量最大,所以乙厂2022至2023年间工业产值增长最快。
15.(1) 13 14
(2) 10 10 14
【分析】(1)分别算出每个年龄小强的体重增长量,再比较大小即可确定几岁至几岁体重增长幅度最大;
(2)根据统计图可知,找出图中实线和虚线的交点对应的年龄就是小强的体重正好是标稚体重的年龄;实线在虚线上方的部分就是小强的体重高于标准体重的年龄段,据此解答。
【详解】(1)24-22=2(千克)
28-24=4(千克)
33-28=5(千克)
37-33=4(千克)
44-37=7(千克)
53-44=9(千克)
2<4<5<7<9
小强13岁至14岁这一年内体重增长幅度最大。
(2)小强10岁时的体重正好是标稚体重,10岁到14岁时的体重高于标准体重。
16.(1)3
(2)1.5
(3)18
【分析】(1)观察折线统计图可知,从第2小时到第5小时小明一直在离家18千米的景区,求出时间差就是小明在景区玩耍的时间;
(2)观察折线统计图可知,小明从家到景区用了2小时,其中第1小时到第1.5小时小明在休息,用总时间减去休息时间就是小明不休息从家到景区用的时间;
(3)第5小时小明从景区出发直接回家,第6小时到家,中间刚好1个小时,小明的行驶路程是从家到景区的距离,据此解答。
【详解】(1)5-2=3(小时)
所以,小明在景区玩了3小时。
(2)2-(1.5-1)
=2-0.5
=1.5(小时)
所以,如果小明途中不休息,1.5小时就可以到达景区。
(3)分析可知,小明返回时每小时行18千米。
17.×
【分析】根据折线统计图的特点及作用,折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段把各点顺次连接起来;折线统计图不仅可以表示数量的多少,还能清楚地反映熟练的增减变化的趋势。据此判断。
【详解】任何一幅复式折线统计图都能分成两幅单式折线统计图,但是任意两个单式折线统计图不一定合成一个复式折线统计图,只有两个有联系的单式统计图才能合成一个复式统计图。
因此,任意两个折线统计图都可以合成一个复式折线统计图。这种说法是错误的。
故答案为:×。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用。
18.√
【分析】复式折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,以折线的上升或下降来表示统计数量增减变化。
【详解】根据分析可知,在复式折线统计图中,两条折线相交的点表示数量相等。
故答案为:√
【点睛】折线统计图不但可以表示出数量的多少,而且还能够清楚的表示出数量增减变化的情况。
19.√
【分析】折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况。
【详解】因为要记录气温的增减变化情况,所以用折线统计图合适。原题说法正确。
故答案为:正确。
【点睛】掌握各种统计图的特点是解题关键。
20.×
【详解】折线统计图易看出数量的增减变化情况,条形统计图易看出数量的多少。
故答案为:×
21.x=50;x=0.11;x=1.1
【分析】(1)根据等式的性质1,方程两边同时加上25,再减去18即可解答;
(2)先把方程左边化简为11x,再根据等式的性质2,方程两边同时除以11即可解答;
(3)先计算0.7×5=3.5,根据等式的性质1,方程两边同时减去3.5,再根据等式的性质2,方程两边同时除以5即可解出方程。
【详解】
解:
x+18=68
x+18-18=68-18
x=50
解:11x=1.21
11x÷11=1.21÷11
x=0.11
解:3.5+5x=9
3.5+5x-3.5=9-3.5
5x=5.5
5x÷5=5.5÷5
x=1.1
22.见详解
【分析】任意选择一个北方的城市以及南方的城市一年中的每个月的降水量,再根据统计图的数据得出结论即可(此题答案不唯一)。
【详解】
根据图中的数据,能获得我国南方降水量比北方多,不论是南方还是北方,总的来说,降水主要集中在夏季(此题答案不唯一)。
23.(1)5
(2)6;22
(3)16.6
【分析】(1)由统计图纵轴数据观察可知,纵轴上每个单位长度表示5℃;
(2)由统计图观察并计算出各个时间段的温度差然后比较大小;
(3)把甲市从6时至22时5个时间段的温度加在一起,用总温度数除以5就是甲市这一天的平均气温。
【详解】(1)纵轴上每个单位长度表示5℃。
(2)6时:14-7=7℃
10时:18-12=6℃
14时:24-18=6℃
18时:16-10=6℃
22时:11-7=4℃
甲市和乙市这一天6时气温相差最大,22时气温相差最小。
(3)(14+18+24+16+11)÷5
=83÷5
=16.6(℃)
所以,根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是16.6℃。
24.(1)小强
(2)先快;慢
(3)小刚;3;小强;100
(4)178米/分;145米/分。
【分析】观察折线统计图可以得出每个时间阶段小刚和小强行驶的路程,由此可以解决问题。此题考查了利用折线统计图表达行驶路程与时间关系及利用统计图中数据解决实际问题的方法。
【详解】(1)行驶800米小强用了4.5分钟,小刚用了5.5分钟,所以小强先到达终点。
(2)根据观察折线统计图发现,比赛时小刚是先快后慢。
(3)开赛初小刚领先,开赛3分钟后小强领先,当小强到达终点时,两人相距最远约为800﹣700=100(米),
(4)800÷4.5≈178(米/分),
800÷5.5≈145(米/分);
答:小强的平均速度是178米/分,小刚的平均速度是145米/分。
25.(1)50%;(2)14904元
【分析】(1)求九月销量比八月下降百分之几,也就是求九月比八月下降了的占八月份销量的百分之几;
(2)先求出商店五个月的总销售量,进而求得营业额,再求出税后收入即可。
【详解】(1)(160﹣80)÷160,
=80÷160,
=50%;
答:九月销量比八月下降50%。
(2)(60+90+150+160+80)×30×(1﹣8%),
=540×30×92%,
=16200×0.92,
=14904(元);
答:商店五个月营业额的税后收入是14904元。
【点睛】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元折线统计图
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.要反映商场不同品牌空调的销售量情况,选择( )比较合适.
A.条形统计图 B.折线统计图
C.两种都可以
2.要反映本次考试优、良、中、差各段学生人数,应该绘制( )。
A.折线统计图 B.条形统计图 C.统计表
3.从一个城市的一周气温情况折线统计图中,不能看出( ).
A.这周气温变化趋势 B.这周哪天气温最高
C.气温变化的原因
4.星期天,小明的爸爸去了一趟相距15千米的老家看望奶奶。他出行的路程和时间的关系如图所示,下面对他的出行方式描述正确的是( )。
A.去时骑自行车,返回时乘公共汽车 B.去时骑自行车,返回时步行
C.去时步行,返回时乘公共汽车 D.去时乘公共汽车,返回时骑自行车
5.要了解小丽在六年级全年的数学成绩变化,选择( )较合适。
A.条形统计图 B.折线统计图 C.扇形统计图
6.小明和小芳骑车从学校沿同一路线到20千米外的公园,已知小明比小芳先出发,他俩所行的路程与时间的关系如图所示。下面说法正确的是( )。
A.他们都骑车行了20千米 B.小明在中途停留了1小时
C.两人同时到达森林公园 D.小芳平均每小时行8千米
7.如图是甲、乙两架航模飞机的飞行情况统计图,第( )秒两架飞机的高度相差最大。
A.20 B.25 C.30 D.35
8.小军从家出发去书店买书,当他走了大约一半路程时。想起忘了带钱。于是他回家取钱,然后再去书店,买了几本书后回家。下面( )幅图比较准确地反映了小军的行为。
A. B. C.
二、填空题
9.统计一周内日平均气温的变化情况,应选择 统计图。
10.折线统计图有 和 两种。
11.龙一鸣和淘淘赛跑情况如图所示。
请回答下面问题。
(1)用“快”“慢”来描述他们的比赛情况:龙一鸣是先( )后( ),淘淘是先( )后( )。
(2)龙一鸣的平均速度是每分( )米,淘淘的平均速度是每分( )米。(保留整数)
12.折线统计图分为 折线统计图和 折线统计图。
13.下面是好运公司2001年各月利润情况折线统计图。
① 月的利润最多,是 万元。
② 月的利润最少,是 万元。
14.下面是甲、乙两家工厂近几年工业产值变化情况统计图,看图回答问题。
(1)2018年两家工厂的工业产值都是( )万元。2022年甲厂的工业产值是( )万元,2022年乙厂的工业产值是( )万元。
(2)2018至2022年间( )厂的工业产值增长得快。
(3)乙厂( )至( )年间工业产值增长最快。
15.小强每年生日都测量体重,下面是他8—14岁生日测量的体重与全国同龄男生标准体重对比统计图。
(1)小强( )岁至( )岁这一年内体重增长幅度最大。
(2)小强( )岁时的体重正好是标稚体重,( )岁到( )岁时的体重高于标准体重。
16.小明骑车从家出发,去离家18千米的景区春游,请根据下面的折线图回答下列问题。
(1)小明在景区玩了( )小时。
(2)如果小明途中不休息,( )小时就可以到达景区。
(3)小明返回时每小时行( )千米。
三、判断题
17.任意两个折线统计图都可以合成一个复式折线统计图。( )
18.在复式折线统计图中,两条折线相交的点表示数量相等。( )
19.要记录6月份每天的气温变化情况,选用折线统计图最合适。( )
20.折线统计图易看出数量的多少,条形统计图易看出数量的增减变化情况。( )
四、计算题
21.解方程。
五、解答题
22.在我国的南方和北方各选一座城市,了解这两座城市去年每月的降水量,完成下面的统计图。
根据图中的数据,你能得出什么结论?
23.甲市和乙市某天6~22时的气温变化情况如图所示。
(1)纵轴上每个单位长度表示( )℃。
(2)甲市和乙市这一天( )时气温相差最大,( )时气温相差最小。
(3)根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是( )℃。
24.小刚和小强赛跑情况如下图
(1)________先到达终点。
(2)请用“快”、“慢”来描述他们的比赛情况:小刚是________后________
(3)开赛初________领先,开赛________分后________领先,比赛中两人相距最远约是________米。
(4)两人的平均速度分别是每分多少米?(保留整数)
25.看统计图回答问题。
(1)九月销量比八月下降百分之几?
(2)每件游泳衣售价30元,按8%的税率缴纳营业税,商店五个月营业额的税后收入是多少元?
《第二单元折线统计图》参考答案
题号 1 2 3 4 5 6 7 8
答案 A B C D B A C C
1.A
【详解】略
2.B
【详解】因为条形统计图能很容易看出数量的多少,所以要反映本次考试优、良、中、差各段学生人数,应该绘制条形统计图。条形统计图能很容易看出数量的多少,关键是掌握条形统计图的特点。
故答案为:B
3.C
【详解】略
4.D
【分析】由路程、速度和时间三者之间的关系可知,速度=路程÷时间。根据题意可知,步行速度应小于骑自行车速度小于乘公共汽车的速度。在图中,当横轴代表时间,纵轴代表路程时,线段越陡,速度越快。据此解答。
【详解】小明家与奶奶家的距离为15千米,距离较远应骑自行车或乘公共汽车。
读图可知:
第一段线段,表示从家去奶奶家,所用时间较少,速度较快,应乘公共汽车;
第二段线段,表示在奶奶家停留,距离不发生变化;
第三段线段,表示从奶奶家返回,所用时间较长,速度较慢,应骑自行车;
所以,去时乘公共汽车,返回时骑自行车。
故答案为:D
5.B
【分析】条形统计图能直观反映出数据的多少,折线统计图不仅能反映数据的多少,还能体现出数据增减变化趋势,扇形统计图能反映出部分与整体之间的数量关系,据此即可得出答案。
【详解】要了解小丽在六年级全年的数学成绩变化,即要选择能反映数据增减变化趋势的统计图,则折线统计图较合适。
故答案为:B
6.A
【分析】A.观察复式折线统计图,数轴表示路程,小明和小芳数据点最高的位置表示总路程;
B.折线往上表示正在骑行,折线平缓无变化,表示中途停留,根据终点时间-起点时间=经过时间,计算出停留时间;
C.实线表示小明数据,虚线表示小芳数据,小明2小时到达公园,小芳2.5小时到达公园,据此分析;
D.先计算出小芳骑行时间,根据路程÷时间=速度,列式计算即可。
【详解】A.他们都骑车行了20千米,说法正确;
B.小明在中途停留了0.5小时,选项说法错误;
C.小明比小芳先到达森林公园,选项说法错误;
D.20÷(2.5-0.5)
=20÷2
=10(千米)
小芳平均每小时行10千米,选项说法错误。
说法正确的是他们都骑车行了20千米。
故答案为:A
7.C
【详解】在第30秒两架飞机的高度相差最大,相差27﹣8=19(米)。
故选:C.
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
8.C
【分析】离家的距离是随时间是这样变化的:
(1)先离家越来越远,到了最远距离一半的时候;(2)然后越来越近直到为0;(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;(4)然后再离家越来越远,直到书店;(5)在书店买书还要一段时间,所以离家最远的时候也是一条水平线段;(6)然后回家直到离家的距离为0。
【详解】符合小军这段时间离家距离变化的是C。
故选: C
【点睛】本题需要考虑到在家和在书店都有一段时间离家的距离不会变化。
9.折线
【详解】略
10. 单式折线统计图; 复式折线统计图
【详解】单式折线统计图只表示一种量,复式折线统计图表示两种或两种以上的量。
11.(1) 快 慢 慢 快
(2) 145 178
【分析】(1)实线表示淘淘,虚线表示龙一鸣,根据折线统计图可知,在400米时,淘淘用了2.5分钟,龙一鸣用了2分钟,到达终点时,淘淘用了4.5分钟,龙一鸣用了5.5分钟,所以龙一鸣的比赛情况是先快后慢;淘淘是先慢后快,据此解答即可;
(2)可根据路程÷时间=速度进行计算即可得到答案。
【详解】(1)龙一鸣先快后慢,淘淘是先慢后快。
(2)800÷5.5≈145(米/分)
800÷4.5≈178(米/分)
即龙一鸣的平均速度是145米/分,淘淘的平均速度是178米/分。
【点睛】此题主要考查的是如何从折线统计图中获取信息,然后再分析计算即可。
12. 单式 复式
【详解】以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图,折线统计图可以分为单式折线统计和复式折线统计图两种。
13. 10 50 4 20
【分析】从折线图中可以直接看出和读出数据。
【详解】横轴表示的是月份,纵轴表示的是利润,所以从图中可以直接出,10月的利润最多,是50万元;4月的利润最少,是20万元。
14.(1) 500 2500 1500
(2)甲
(3) 2022 2023
【分析】(1)观察统计图中折线的走势和对应的数据点来回答问题;先从统计图中读取特定年份的产值数据回答:
(2)分别计算甲、乙两厂在2018-2022年间的产值增长量,再比较大小;
(3)最后计算乙厂各相邻年份间的产值增长量,找出增长最快的时间段。
【详解】(1)观察统计图可知,在2018年这个时间点,甲厂和乙厂对应的产值都是500万元。
在统计图中,2022年甲厂对应的产值是2500万元,2022年乙厂对应的产值是1500万元。
(2)2500-500=2000(万元)
1500-500=1000(万元)
2000>1000
所以2018至2022年间甲厂的工业产值增长得快。
(3)2018-2019年乙厂产值为625万元,2018年为500万元,增长量:625-500=125(万元)。
计算乙厂2019-2020年间的产值增长量:2020年乙厂产值为1000万元,2019年为625万元,增长量=1000-625=375(万元)。
计算乙厂2020-2021年间的产值增长量:2021年乙厂产值为1125万元,2020年为1000万元,增长量=1125-1000=125(万元)。
计算乙厂2021-2022年间的产值增长量:2022年乙厂产值为1500万元,2021年为1125万元,增长量=1500-1125 = 375(万元)。
计算乙厂2022-2023年间的产值增长量:2022年乙厂产值为1500万元,2023年为2500万元,增长量:2500-1500=1000(万元)
比较各时间段的增长量125<375<1000,可知:2022-2023年间增长量最大,所以乙厂2022至2023年间工业产值增长最快。
15.(1) 13 14
(2) 10 10 14
【分析】(1)分别算出每个年龄小强的体重增长量,再比较大小即可确定几岁至几岁体重增长幅度最大;
(2)根据统计图可知,找出图中实线和虚线的交点对应的年龄就是小强的体重正好是标稚体重的年龄;实线在虚线上方的部分就是小强的体重高于标准体重的年龄段,据此解答。
【详解】(1)24-22=2(千克)
28-24=4(千克)
33-28=5(千克)
37-33=4(千克)
44-37=7(千克)
53-44=9(千克)
2<4<5<7<9
小强13岁至14岁这一年内体重增长幅度最大。
(2)小强10岁时的体重正好是标稚体重,10岁到14岁时的体重高于标准体重。
16.(1)3
(2)1.5
(3)18
【分析】(1)观察折线统计图可知,从第2小时到第5小时小明一直在离家18千米的景区,求出时间差就是小明在景区玩耍的时间;
(2)观察折线统计图可知,小明从家到景区用了2小时,其中第1小时到第1.5小时小明在休息,用总时间减去休息时间就是小明不休息从家到景区用的时间;
(3)第5小时小明从景区出发直接回家,第6小时到家,中间刚好1个小时,小明的行驶路程是从家到景区的距离,据此解答。
【详解】(1)5-2=3(小时)
所以,小明在景区玩了3小时。
(2)2-(1.5-1)
=2-0.5
=1.5(小时)
所以,如果小明途中不休息,1.5小时就可以到达景区。
(3)分析可知,小明返回时每小时行18千米。
17.×
【分析】根据折线统计图的特点及作用,折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段把各点顺次连接起来;折线统计图不仅可以表示数量的多少,还能清楚地反映熟练的增减变化的趋势。据此判断。
【详解】任何一幅复式折线统计图都能分成两幅单式折线统计图,但是任意两个单式折线统计图不一定合成一个复式折线统计图,只有两个有联系的单式统计图才能合成一个复式统计图。
因此,任意两个折线统计图都可以合成一个复式折线统计图。这种说法是错误的。
故答案为:×。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用。
18.√
【分析】复式折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,以折线的上升或下降来表示统计数量增减变化。
【详解】根据分析可知,在复式折线统计图中,两条折线相交的点表示数量相等。
故答案为:√
【点睛】折线统计图不但可以表示出数量的多少,而且还能够清楚的表示出数量增减变化的情况。
19.√
【分析】折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况。
【详解】因为要记录气温的增减变化情况,所以用折线统计图合适。原题说法正确。
故答案为:正确。
【点睛】掌握各种统计图的特点是解题关键。
20.×
【详解】折线统计图易看出数量的增减变化情况,条形统计图易看出数量的多少。
故答案为:×
21.x=50;x=0.11;x=1.1
【分析】(1)根据等式的性质1,方程两边同时加上25,再减去18即可解答;
(2)先把方程左边化简为11x,再根据等式的性质2,方程两边同时除以11即可解答;
(3)先计算0.7×5=3.5,根据等式的性质1,方程两边同时减去3.5,再根据等式的性质2,方程两边同时除以5即可解出方程。
【详解】
解:
x+18=68
x+18-18=68-18
x=50
解:11x=1.21
11x÷11=1.21÷11
x=0.11
解:3.5+5x=9
3.5+5x-3.5=9-3.5
5x=5.5
5x÷5=5.5÷5
x=1.1
22.见详解
【分析】任意选择一个北方的城市以及南方的城市一年中的每个月的降水量,再根据统计图的数据得出结论即可(此题答案不唯一)。
【详解】
根据图中的数据,能获得我国南方降水量比北方多,不论是南方还是北方,总的来说,降水主要集中在夏季(此题答案不唯一)。
23.(1)5
(2)6;22
(3)16.6
【分析】(1)由统计图纵轴数据观察可知,纵轴上每个单位长度表示5℃;
(2)由统计图观察并计算出各个时间段的温度差然后比较大小;
(3)把甲市从6时至22时5个时间段的温度加在一起,用总温度数除以5就是甲市这一天的平均气温。
【详解】(1)纵轴上每个单位长度表示5℃。
(2)6时:14-7=7℃
10时:18-12=6℃
14时:24-18=6℃
18时:16-10=6℃
22时:11-7=4℃
甲市和乙市这一天6时气温相差最大,22时气温相差最小。
(3)(14+18+24+16+11)÷5
=83÷5
=16.6(℃)
所以,根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是16.6℃。
24.(1)小强
(2)先快;慢
(3)小刚;3;小强;100
(4)178米/分;145米/分。
【分析】观察折线统计图可以得出每个时间阶段小刚和小强行驶的路程,由此可以解决问题。此题考查了利用折线统计图表达行驶路程与时间关系及利用统计图中数据解决实际问题的方法。
【详解】(1)行驶800米小强用了4.5分钟,小刚用了5.5分钟,所以小强先到达终点。
(2)根据观察折线统计图发现,比赛时小刚是先快后慢。
(3)开赛初小刚领先,开赛3分钟后小强领先,当小强到达终点时,两人相距最远约为800﹣700=100(米),
(4)800÷4.5≈178(米/分),
800÷5.5≈145(米/分);
答:小强的平均速度是178米/分,小刚的平均速度是145米/分。
25.(1)50%;(2)14904元
【分析】(1)求九月销量比八月下降百分之几,也就是求九月比八月下降了的占八月份销量的百分之几;
(2)先求出商店五个月的总销售量,进而求得营业额,再求出税后收入即可。
【详解】(1)(160﹣80)÷160,
=80÷160,
=50%;
答:九月销量比八月下降50%。
(2)(60+90+150+160+80)×30×(1﹣8%),
=540×30×92%,
=16200×0.92,
=14904(元);
答:商店五个月营业额的税后收入是14904元。
【点睛】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
