北师大版2024—2025学年八年级下学期数学期末复习押题卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年八年级下学期数学期末复习押题卷(含答案) | 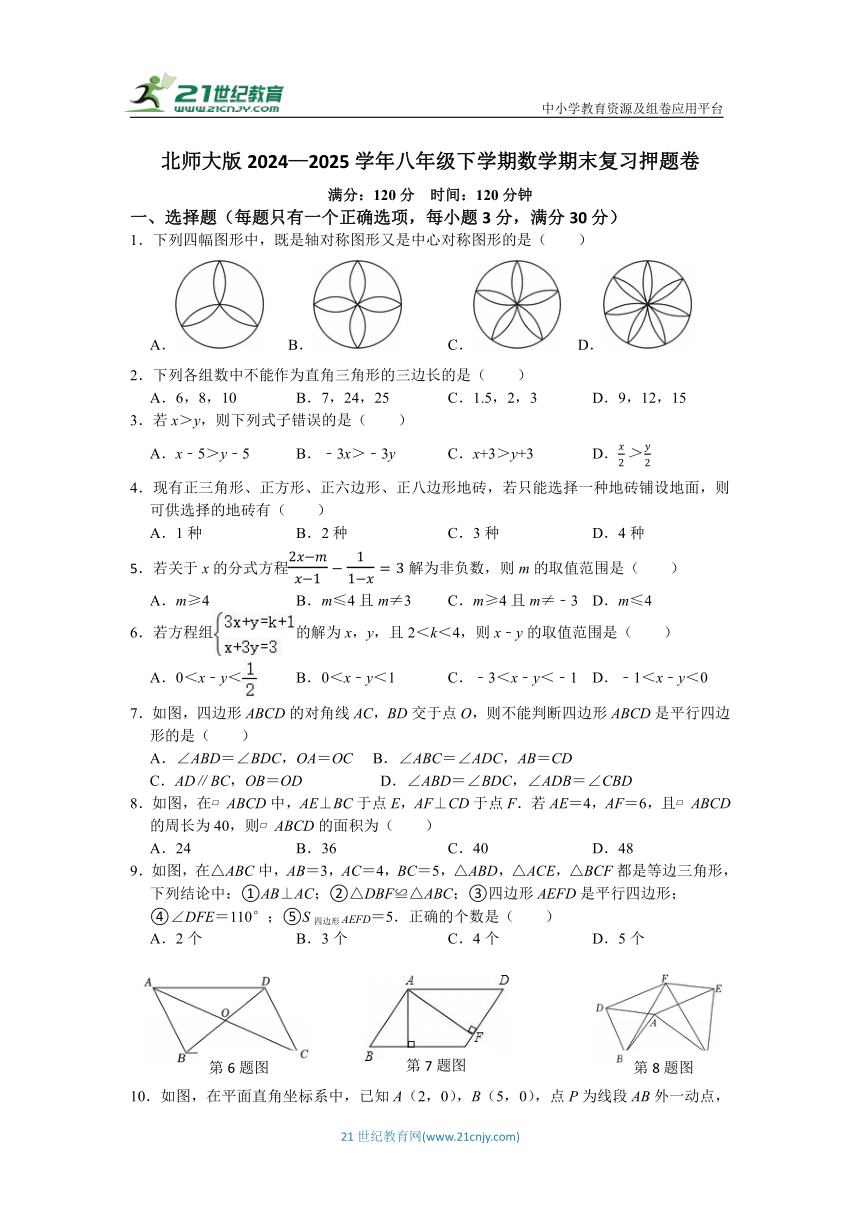 | |
| 格式 | docx | ||
| 文件大小 | 636.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 21:05:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年八年级下学期数学期末复习押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四幅图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
3.若x>y,则下列式子错误的是( )
A.x﹣5>y﹣5 B.﹣3x>﹣3y C.x+3>y+3 D.
4.现有正三角形、正方形、正六边形、正八边形地砖,若只能选择一种地砖铺设地面,则可供选择的地砖有( )
A.1种 B.2种 C.3种 D.4种
5.若关于x的分式方程解为非负数,则m的取值范围是( )
A.m≥4 B.m≤4且m≠3 C.m≥4且m≠﹣3 D.m≤4
6.若方程组的解为x,y,且2<k<4,则x﹣y的取值范围是( )
A.0<x﹣y< B.0<x﹣y<1 C.﹣3<x﹣y<﹣1 D.﹣1<x﹣y<0
7.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD D.∠ABD=∠BDC,∠ADB=∠CBD
8.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
9.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②△DBF≌△ABC;③四边形AEFD是平行四边形;
④∠DFE=110°;⑤S四边形AEFD=5.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
10.如图,在平面直角坐标系中,已知A(2,0),B(5,0),点P为线段AB外一动点,且PA=2,以PB为边作等边△PBM,则线段AM的最大值为( )
A.3 B.5 C.7 D.
二、填空题(每小题3分,满分18分)
11.若不等式(m﹣2024)x>m﹣2024两边同时除以(m﹣2024),得x<1,则m的取值范围是 .
12.若点P(a﹣2,5)在第二象限,且a为正整数,则a的值为 .
13.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= .
14.如图,已知BO平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,AC=18,则△AMN的周长是 .
15.若关于x的不等式组无解,则a的取值范围为 .
16.某种商品的进价为400元,出售时标价为500元,商店准备打折出售,但要保持利润率不低于10%,则至多可以打 折.
第II卷
北师大版2024—2025学年八年级下学期数学期末复习押题卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
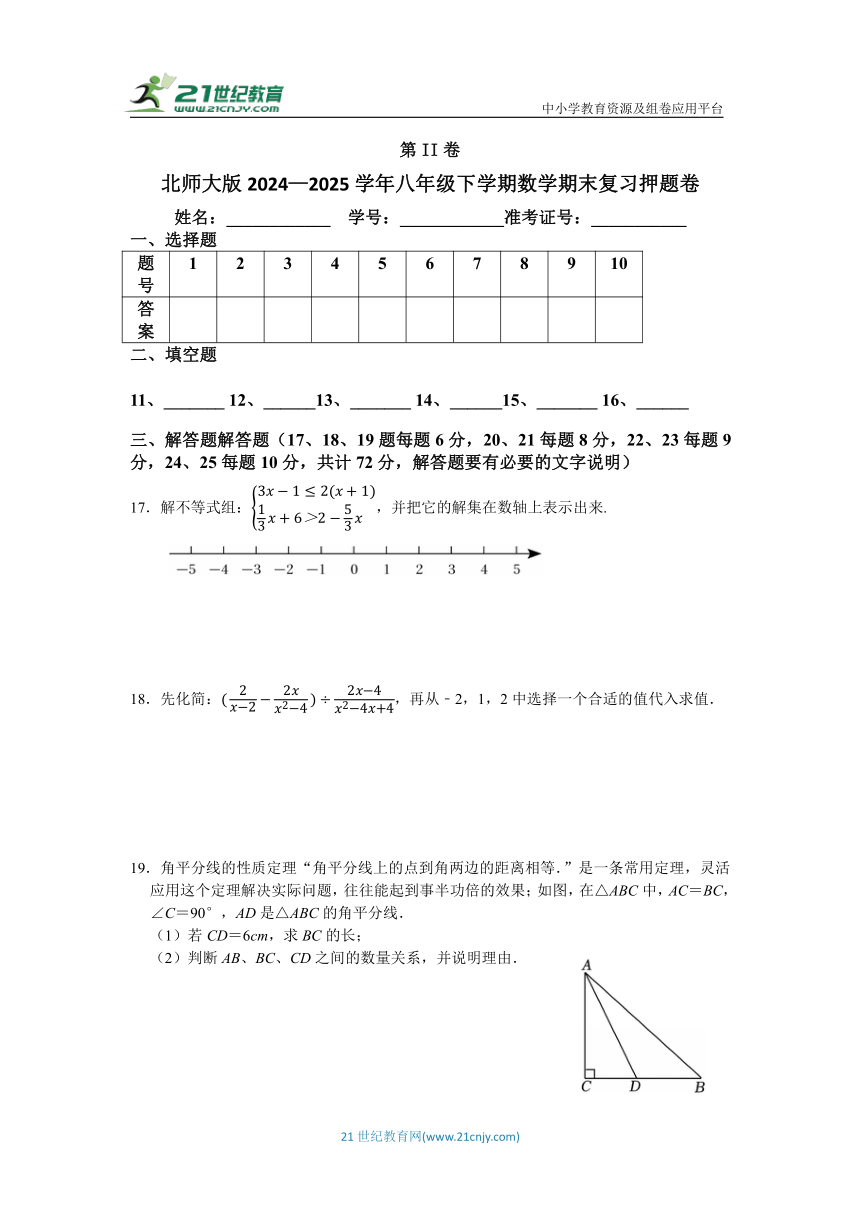
17.解不等式组:,并把它的解集在数轴上表示出来.
18.先化简:,再从﹣2,1,2中选择一个合适的值代入求值.
19.角平分线的性质定理“角平分线上的点到角两边的距离相等.”是一条常用定理,灵活应用这个定理解决实际问题,往往能起到事半功倍的效果;如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线.
(1)若CD=6cm,求BC的长;
(2)判断AB、BC、CD之间的数量关系,并说明理由.
20.如图,在平面直角坐标系中xOy,已知△ABC三个顶点的坐标分别为A(1,3),B(﹣1,1),C(﹣2,2).
(1)画出△ABC绕原点O顺时针旋转90°得到的△A1B1C1;
(2)在y轴上取点P,使△ABP的面积是△ABC面积的倍,求点P的坐标.
21.2024年汤尤杯比赛于4月27日至5月5日在成都高新体育中心举行.作为世界羽毛球界的重要赛事,它的周边产品(如熊猫挂件)深受球迷喜爱.已知每件A型熊猫挂件比每件B型熊猫挂件多15元,用1200元购买的A型熊猫挂件与900元购买的B型熊猫挂件数量相同.
(1)每件A型熊猫挂件与每件B型熊猫挂件的售价是多少元?
(2)若某球迷决定用不超过2000元购买A,B两种型号的熊猫挂件共40件,则最多购买A型熊猫挂件多少件?
22.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边在AB上方作等边△ABD,点F是线段AD的中点,连接CF.
(1)若AC=3,求AD的长;
(2)求证:四边形BCFD是平行四边形.
23.定义新运算:x*y=ax+by,且1*2=0,(﹣1)*1=3.
(1)求a,b的值;
(2)若0<c*(c+3)<2,求c的取值范围;
(3)图中的数轴上墨迹恰好遮住了关于m的不等式|(2m﹣1)*(2﹣m)|<n+1的所有整数解,求整数n的值.
24.如图,已知 ABCD的周长为4+4,ABAD.
(1)求线段BC的长;
(2)若∠ABC=45°,连接BD,在线段BD上取一点E,连接CE.
(ⅰ)当△CDE是以CD为斜边的直角三角形时,求CE的长;
(ⅱ)作 DECF,连接AF,试问:是否存在点E,使得CF+DFAF?若存在,求出此时AF的长;若不存在,请说明理由.
25.新定义:如果两个实数a,b使得关于x的分式方程的解是成立,那么我们就把实数a,b组成的数对[a,b]称为关于x的分式方程的一个“关联数对”.
例如:a=2,b=﹣5使得关于x的分式方程的解是成立,所以数对[2,﹣5]就是关于x的分式方程的一个“关联数对”.
(1)判断下列数对是否为关于x的分式方程的“关联数对”,若是,请在括号内打“√”;若不是,打“×”.①[3,﹣5]( );②[1,﹣2]( ).
(2)若数对是关于x的分式方程的“关联数对”,求n的值.
(3)若数对[2m+k,﹣k](,且m≠0,k≠﹣1)是关于x的分式方程的“关联数对”,且关于x的方程有整数解,求整数m的值.
参考答案
一、选择题
1—10:BCBCB CBDBB
二、填空题
11.【解答】解:由题意得:m﹣2024<0,
解得:m<2024,
故答案为:m<2024.
12.【解答】解:∵点P(a﹣2,5)在第二象限,
∴a﹣2<0,
解得a<2,
∵a为正整数,
∴a=1,
故答案为:1.
13.【解答】解:∵△ABC为等边三角形,BD为△ABC的高,
∴点D为AC的中点,AC=BC,
∵CE=CD=1,
∴AC=2CD=2,
∴BC=2,
∴BE=BC+CE=2+1=3,
故答案为:3.
14.【解答】解:∵BO平分∠CBA,CO平分∠ACB,
∴∠NBO=∠OBC,∠OCM=∠OCB,
∵MN∥BC,
∴∠NOB=∠OBC,∠MOC=∠OCB,
∴∠NBO=∠NOB,∠MOC=∠MCO,
∴MO=MC,NO=NB,
∵AB=12,AC=18,
∴△AMN的周长=AM+MN+AN=AM+OM+ON+AN=AB+AC=18+12=30,
故答案为:30.
15.【解答】解:∵关于x的不等式组无解,
∴a﹣1≥2,
∴a≥3,
故答案为:a≥3.
16.【解答】解:要保持利润率不低于10%,设可打x折.
则500400≥400×10%,
解得x≥8.8.
故答案为:8.8.
三、解答题
17.【解答】解:∵解不等式3x﹣1≤2(x+1)得:x≤3,
解不等式x+6>2x得:x>﹣2,
∴不等式组的解集是﹣2<x≤3,
在数轴上表示不等式组的解集是.
18.【解答】解:
,
∵x≠2,﹣2,
∴x=1,
∴原式.
19.【解答】解:(1)过D点作DE⊥AB于点E,则∠AED=∠BED=90°,
在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线.
∴DE=CD=6cm,∠B=45°,
∴△BDE为等腰直角三角形,
∴BE=DE=6cm,
∴BD(cm),
∴BC=CD+BD=()cm;
(2)AB=BC+CD,
理由:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,
∵BE=DE=CD,
∴AB=AE+BE=AC+CD=BC+CD,
20.【解答】解:(1)如图,△A1B1C1即为所求.
(2)△ABC的面积为(1+2)×32=2.
设点P的坐标为(0,m),
∵△ABP的面积是△ABC面积的倍,
∴,
解得m=5或﹣1,
21.【解答】解:(1)设每件B型熊猫挂件的售价是x元,则每件A型熊猫挂件的售价是(x+15)元,
根据题意得:,
解得:x=45,
经检验,x=45是所列方程的解,且符合题意,
∴x+15=45+15=60.
答:每件A型熊猫挂件的售价是60元,每件B型熊猫挂件的售价是45元;
(2)设购买y件A型熊猫挂件,则购买(40﹣y)件B型熊猫挂件,
根据题意得:60y+45(40﹣y)≤2000,
解得:y,
又∵y为正整数,
∴y的最大值为13.
答:最多购买A型熊猫挂件13件.
22.【解答】(1)解:∵∠ACB=90°,∠CAB=30°,
∴BCAB,
设BC=x,则AB=2x,
∴BC2+AC2=AB2,
即x2+32=(2x)2,
解得x(舍去负值),
即BC,AB=2,
∵△ABD是等边三角形,
∴AB=AD=2;
(2)证明:∵∠ACB=90°,∠CAB=30°,
∴BCAB,∠ABC=60°,
∵△ABD是等边三角形,
∴∠ABD=∠BAD=60°,AB=AD,
∴∠ABC=∠BAD,
∴BC∥DA,
∵点E是线段AB的中点,
∴CEAB=BE=AE,
∵∠ABC=60°,即∠EBC=60°,
∴△BCE是等边三角形,
∴∠BEC=60°=∠ABD,
∴BD∥CF,且BC∥DA
∴四边形BCFD为平行四边形.
23.【解答】解:(1)依题意,有,
解得;
(2)由(1)得x*y=﹣2x+y,
∵0<c*(c+3)<2,
∴0<﹣2c+(c+3)<2,
解得1<c<3;
(3)∵|(2m﹣1)*(2﹣m)|<n+1,
∴|﹣2(2m﹣1)+(2﹣m)|=|﹣5m+4|<n+1,
∴﹣n﹣1<﹣5m+4<n+1,
解得<m<,
∴数轴上墨迹遮住的整数有﹣2,﹣1,1,0,1,2,3,
∴<m<的整数解为﹣2,﹣1,1,0,1,2,3,
,
解得:13<n≤15,
∴整数n的值为14或15.
24.【解答】解:(1)∵ ABCD的周长为4+4,
∴2(AB+AD)=4+4,
∴AB+AD,
∵ABAD,
∴AD=2,AB,
∴BC=AD=2;
(2)(i)过点D作DH⊥BC交BC延长线于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DCH=∠ABC=45°,
∴DH=CH,
∴BH=BC+CH=4,
∴BD,
∵,
∴,
∴CE;
(ii)由(i)得DH=2,AB,
∴AC=2,即AC⊥BC,
∴∠BAC=45°,
∴∠DAC=90°,
将△ADF绕点A顺时针旋转90°,得到△ACG,若F,G,C三点共线,则CF+DFAF成立.
∵∠DAC=90°,
∴当∠DFC=90°时,F,G,C三点共线,
即当CE⊥BD时,成立,
此时CECG,
∴BE,
∴DE,
∴FG,
∴AF.
25.【解答】解:(1)当a=3,b=﹣5时,
分式方程,解得,
∵,
∴①的答案是√;
当a=1,b=﹣2时,
分式方程,解得,
∵,
∴②的答案是×;
故答案为:√;×;
(2)∵数对是关于x的分式方程的“关联数对”,
∴a=﹣n,,
∴,解得,
∵,
∴,
解得n=3;
(3)∵数对[2m+k,﹣k]是关于x的分式方程的“关联数对”,
∴a=2m+k,b=﹣k,
∵k≠﹣1,m≠0,
∴,,
∵,
∴,
当时,解得,
将化简得:(2m﹣1)2x=(1﹣2m)(1+2m),
∵,
解得,
∵关于x的方程有整数解,且m为整数,
∴2m﹣1=±1或±2,
即2m﹣1=﹣1或2m﹣1=1或2m﹣1=﹣2或2m﹣1=2,
解得m=0或m=1或(不是整数,舍去)或(不是整数,舍去),
∵m≠0,
∴m=1.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年八年级下学期数学期末复习押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四幅图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
3.若x>y,则下列式子错误的是( )
A.x﹣5>y﹣5 B.﹣3x>﹣3y C.x+3>y+3 D.
4.现有正三角形、正方形、正六边形、正八边形地砖,若只能选择一种地砖铺设地面,则可供选择的地砖有( )
A.1种 B.2种 C.3种 D.4种
5.若关于x的分式方程解为非负数,则m的取值范围是( )
A.m≥4 B.m≤4且m≠3 C.m≥4且m≠﹣3 D.m≤4
6.若方程组的解为x,y,且2<k<4,则x﹣y的取值范围是( )
A.0<x﹣y< B.0<x﹣y<1 C.﹣3<x﹣y<﹣1 D.﹣1<x﹣y<0
7.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD D.∠ABD=∠BDC,∠ADB=∠CBD
8.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
9.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②△DBF≌△ABC;③四边形AEFD是平行四边形;
④∠DFE=110°;⑤S四边形AEFD=5.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
10.如图,在平面直角坐标系中,已知A(2,0),B(5,0),点P为线段AB外一动点,且PA=2,以PB为边作等边△PBM,则线段AM的最大值为( )
A.3 B.5 C.7 D.
二、填空题(每小题3分,满分18分)
11.若不等式(m﹣2024)x>m﹣2024两边同时除以(m﹣2024),得x<1,则m的取值范围是 .
12.若点P(a﹣2,5)在第二象限,且a为正整数,则a的值为 .
13.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= .
14.如图,已知BO平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,AC=18,则△AMN的周长是 .
15.若关于x的不等式组无解,则a的取值范围为 .
16.某种商品的进价为400元,出售时标价为500元,商店准备打折出售,但要保持利润率不低于10%,则至多可以打 折.
第II卷
北师大版2024—2025学年八年级下学期数学期末复习押题卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解不等式组:,并把它的解集在数轴上表示出来.
18.先化简:,再从﹣2,1,2中选择一个合适的值代入求值.
19.角平分线的性质定理“角平分线上的点到角两边的距离相等.”是一条常用定理,灵活应用这个定理解决实际问题,往往能起到事半功倍的效果;如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线.
(1)若CD=6cm,求BC的长;
(2)判断AB、BC、CD之间的数量关系,并说明理由.
20.如图,在平面直角坐标系中xOy,已知△ABC三个顶点的坐标分别为A(1,3),B(﹣1,1),C(﹣2,2).
(1)画出△ABC绕原点O顺时针旋转90°得到的△A1B1C1;
(2)在y轴上取点P,使△ABP的面积是△ABC面积的倍,求点P的坐标.
21.2024年汤尤杯比赛于4月27日至5月5日在成都高新体育中心举行.作为世界羽毛球界的重要赛事,它的周边产品(如熊猫挂件)深受球迷喜爱.已知每件A型熊猫挂件比每件B型熊猫挂件多15元,用1200元购买的A型熊猫挂件与900元购买的B型熊猫挂件数量相同.
(1)每件A型熊猫挂件与每件B型熊猫挂件的售价是多少元?
(2)若某球迷决定用不超过2000元购买A,B两种型号的熊猫挂件共40件,则最多购买A型熊猫挂件多少件?
22.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边在AB上方作等边△ABD,点F是线段AD的中点,连接CF.
(1)若AC=3,求AD的长;
(2)求证:四边形BCFD是平行四边形.
23.定义新运算:x*y=ax+by,且1*2=0,(﹣1)*1=3.
(1)求a,b的值;
(2)若0<c*(c+3)<2,求c的取值范围;
(3)图中的数轴上墨迹恰好遮住了关于m的不等式|(2m﹣1)*(2﹣m)|<n+1的所有整数解,求整数n的值.
24.如图,已知 ABCD的周长为4+4,ABAD.
(1)求线段BC的长;
(2)若∠ABC=45°,连接BD,在线段BD上取一点E,连接CE.
(ⅰ)当△CDE是以CD为斜边的直角三角形时,求CE的长;
(ⅱ)作 DECF,连接AF,试问:是否存在点E,使得CF+DFAF?若存在,求出此时AF的长;若不存在,请说明理由.
25.新定义:如果两个实数a,b使得关于x的分式方程的解是成立,那么我们就把实数a,b组成的数对[a,b]称为关于x的分式方程的一个“关联数对”.
例如:a=2,b=﹣5使得关于x的分式方程的解是成立,所以数对[2,﹣5]就是关于x的分式方程的一个“关联数对”.
(1)判断下列数对是否为关于x的分式方程的“关联数对”,若是,请在括号内打“√”;若不是,打“×”.①[3,﹣5]( );②[1,﹣2]( ).
(2)若数对是关于x的分式方程的“关联数对”,求n的值.
(3)若数对[2m+k,﹣k](,且m≠0,k≠﹣1)是关于x的分式方程的“关联数对”,且关于x的方程有整数解,求整数m的值.
参考答案
一、选择题
1—10:BCBCB CBDBB
二、填空题
11.【解答】解:由题意得:m﹣2024<0,
解得:m<2024,
故答案为:m<2024.
12.【解答】解:∵点P(a﹣2,5)在第二象限,
∴a﹣2<0,
解得a<2,
∵a为正整数,
∴a=1,
故答案为:1.
13.【解答】解:∵△ABC为等边三角形,BD为△ABC的高,
∴点D为AC的中点,AC=BC,
∵CE=CD=1,
∴AC=2CD=2,
∴BC=2,
∴BE=BC+CE=2+1=3,
故答案为:3.
14.【解答】解:∵BO平分∠CBA,CO平分∠ACB,
∴∠NBO=∠OBC,∠OCM=∠OCB,
∵MN∥BC,
∴∠NOB=∠OBC,∠MOC=∠OCB,
∴∠NBO=∠NOB,∠MOC=∠MCO,
∴MO=MC,NO=NB,
∵AB=12,AC=18,
∴△AMN的周长=AM+MN+AN=AM+OM+ON+AN=AB+AC=18+12=30,
故答案为:30.
15.【解答】解:∵关于x的不等式组无解,
∴a﹣1≥2,
∴a≥3,
故答案为:a≥3.
16.【解答】解:要保持利润率不低于10%,设可打x折.
则500400≥400×10%,
解得x≥8.8.
故答案为:8.8.
三、解答题
17.【解答】解:∵解不等式3x﹣1≤2(x+1)得:x≤3,
解不等式x+6>2x得:x>﹣2,
∴不等式组的解集是﹣2<x≤3,
在数轴上表示不等式组的解集是.
18.【解答】解:
,
∵x≠2,﹣2,
∴x=1,
∴原式.
19.【解答】解:(1)过D点作DE⊥AB于点E,则∠AED=∠BED=90°,
在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线.
∴DE=CD=6cm,∠B=45°,
∴△BDE为等腰直角三角形,
∴BE=DE=6cm,
∴BD(cm),
∴BC=CD+BD=()cm;
(2)AB=BC+CD,
理由:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,
∵BE=DE=CD,
∴AB=AE+BE=AC+CD=BC+CD,
20.【解答】解:(1)如图,△A1B1C1即为所求.
(2)△ABC的面积为(1+2)×32=2.
设点P的坐标为(0,m),
∵△ABP的面积是△ABC面积的倍,
∴,
解得m=5或﹣1,
21.【解答】解:(1)设每件B型熊猫挂件的售价是x元,则每件A型熊猫挂件的售价是(x+15)元,
根据题意得:,
解得:x=45,
经检验,x=45是所列方程的解,且符合题意,
∴x+15=45+15=60.
答:每件A型熊猫挂件的售价是60元,每件B型熊猫挂件的售价是45元;
(2)设购买y件A型熊猫挂件,则购买(40﹣y)件B型熊猫挂件,
根据题意得:60y+45(40﹣y)≤2000,
解得:y,
又∵y为正整数,
∴y的最大值为13.
答:最多购买A型熊猫挂件13件.
22.【解答】(1)解:∵∠ACB=90°,∠CAB=30°,
∴BCAB,
设BC=x,则AB=2x,
∴BC2+AC2=AB2,
即x2+32=(2x)2,
解得x(舍去负值),
即BC,AB=2,
∵△ABD是等边三角形,
∴AB=AD=2;
(2)证明:∵∠ACB=90°,∠CAB=30°,
∴BCAB,∠ABC=60°,
∵△ABD是等边三角形,
∴∠ABD=∠BAD=60°,AB=AD,
∴∠ABC=∠BAD,
∴BC∥DA,
∵点E是线段AB的中点,
∴CEAB=BE=AE,
∵∠ABC=60°,即∠EBC=60°,
∴△BCE是等边三角形,
∴∠BEC=60°=∠ABD,
∴BD∥CF,且BC∥DA
∴四边形BCFD为平行四边形.
23.【解答】解:(1)依题意,有,
解得;
(2)由(1)得x*y=﹣2x+y,
∵0<c*(c+3)<2,
∴0<﹣2c+(c+3)<2,
解得1<c<3;
(3)∵|(2m﹣1)*(2﹣m)|<n+1,
∴|﹣2(2m﹣1)+(2﹣m)|=|﹣5m+4|<n+1,
∴﹣n﹣1<﹣5m+4<n+1,
解得<m<,
∴数轴上墨迹遮住的整数有﹣2,﹣1,1,0,1,2,3,
∴<m<的整数解为﹣2,﹣1,1,0,1,2,3,
,
解得:13<n≤15,
∴整数n的值为14或15.
24.【解答】解:(1)∵ ABCD的周长为4+4,
∴2(AB+AD)=4+4,
∴AB+AD,
∵ABAD,
∴AD=2,AB,
∴BC=AD=2;
(2)(i)过点D作DH⊥BC交BC延长线于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DCH=∠ABC=45°,
∴DH=CH,
∴BH=BC+CH=4,
∴BD,
∵,
∴,
∴CE;
(ii)由(i)得DH=2,AB,
∴AC=2,即AC⊥BC,
∴∠BAC=45°,
∴∠DAC=90°,
将△ADF绕点A顺时针旋转90°,得到△ACG,若F,G,C三点共线,则CF+DFAF成立.
∵∠DAC=90°,
∴当∠DFC=90°时,F,G,C三点共线,
即当CE⊥BD时,成立,
此时CECG,
∴BE,
∴DE,
∴FG,
∴AF.
25.【解答】解:(1)当a=3,b=﹣5时,
分式方程,解得,
∵,
∴①的答案是√;
当a=1,b=﹣2时,
分式方程,解得,
∵,
∴②的答案是×;
故答案为:√;×;
(2)∵数对是关于x的分式方程的“关联数对”,
∴a=﹣n,,
∴,解得,
∵,
∴,
解得n=3;
(3)∵数对[2m+k,﹣k]是关于x的分式方程的“关联数对”,
∴a=2m+k,b=﹣k,
∵k≠﹣1,m≠0,
∴,,
∵,
∴,
当时,解得,
将化简得:(2m﹣1)2x=(1﹣2m)(1+2m),
∵,
解得,
∵关于x的方程有整数解,且m为整数,
∴2m﹣1=±1或±2,
即2m﹣1=﹣1或2m﹣1=1或2m﹣1=﹣2或2m﹣1=2,
解得m=0或m=1或(不是整数,舍去)或(不是整数,舍去),
∵m≠0,
∴m=1.
21世纪教育网(www.21cnjy.com)
同课章节目录
