北师大版2024—2025学年八年级下册数学期末考试预测卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年八年级下册数学期末考试预测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 626.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年八年级下册数学期末考试预测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.把5(a﹣b)+m(b﹣a)提公因式后一个因式是(a﹣b),则另一个因式是( )
A.5﹣m B.5+m C.m﹣5 D.﹣m﹣5
2.若等腰三角形的周长为16cm,其中一边长为4cm,则该等腰三角形的底边为( )
A.4cm B.6cm C.4cm或8cm D.8cm
3.下列不能判定△ABC是直角三角形的是( )
A.a2+b2﹣c2=0 B.a:b:c=3:4:5
C.∠A:∠B:∠C=3:4:5 D.∠A+∠B=∠C
4.分式的值为0,则x的值为( )
A.3 B.﹣3 C.±3 D.9
5.不等式组的解集是( )
A.x>1 B.x≤4 C.x>1或x≤4 D.1<x≤4
6.在平面直角坐标系中,点P(1,2)关于坐标原点的对称点P′的坐标为( )
A.(﹣1,﹣2) B.(﹣1,2) C.(1,﹣2) D.(1,2)
7.若ab=2,,则多项式a3b+2a2b2+ab3的值为( )
A.6 B.12 C.16 D.18
8.关于x的分式方程的解是正数,则m的取值范围是( )
A.m>2且m≠3 B.m>2 C.m≥2且m≠3 D.m≥2
9.已知△ABC的三边长a、b、c满足条件:a4﹣b4=a2c2﹣b2c2,则△ABC的形状是( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
10.如图,四边形ABCD中,∠C=∠BAD=90°,∠B=60°,若CD=2,AD=1,则四边形ABCD的面积为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.若关于x的二次三项式x2﹣px﹣12含有因式(x﹣3),则实数p的值是 .
12.若3mx|2m﹣1|﹣7≥9是关于x的一元一次不等式,则m= .
13.关于x的不等式组的解集为﹣1<x<2,则a﹣b的值为 .
14.如果一个正多边形的内角和为1800°,那么这个正多边形共有对角线 条.
15.如图,Rt△ABC和Rt△DEF重叠在一起,将△DEF沿点B到点C的方向平移到如图位置,已知AB=9.图中阴影部分的面积为15,DH=3,则平移距离为 .
16.如图:在△ABC中,AB=AC=10,BC=12,P是BC边上的动点,过点P作PD⊥AB过于点D,PE⊥AC于点E,则PD+PE的长是 .
第II卷
北师大版2024—2025学年八年级下册数学期末考试预测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
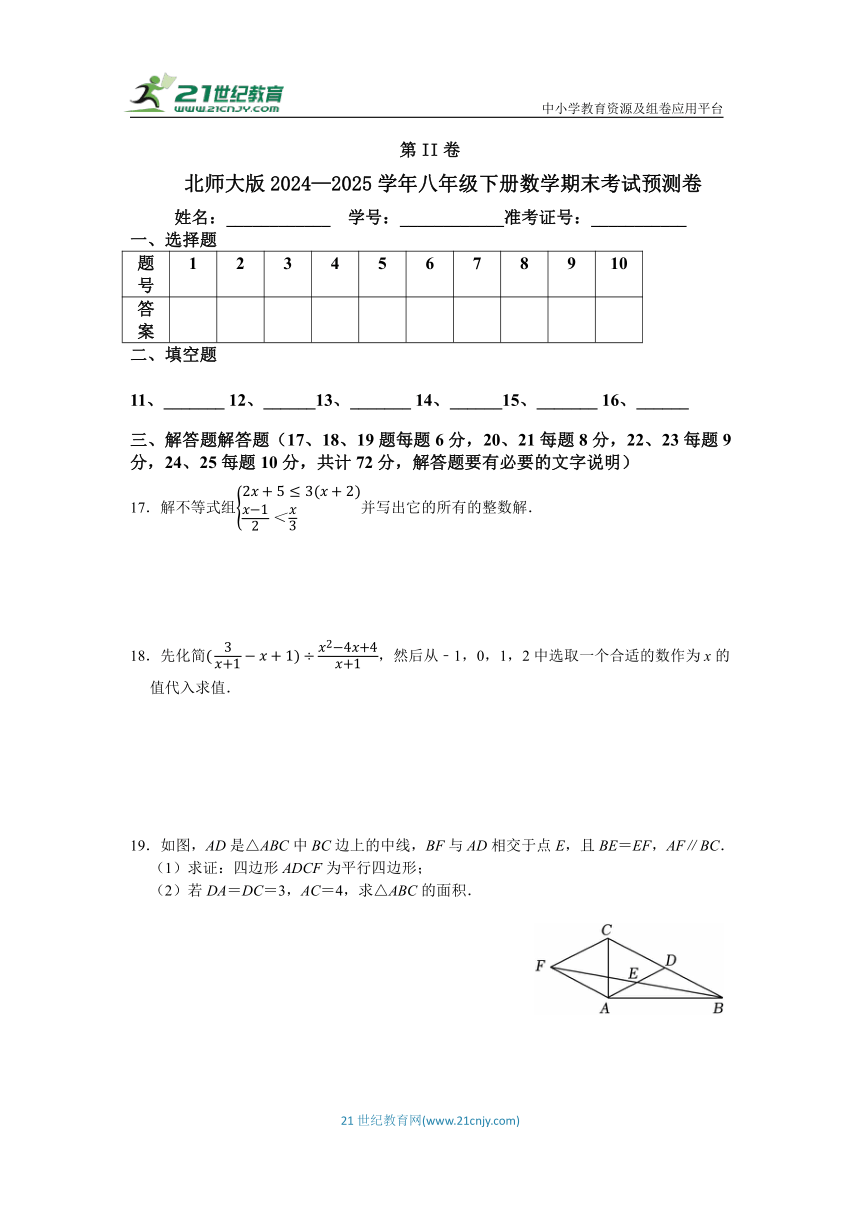
17.解不等式组并写出它的所有的整数解.
18.先化简,然后从﹣1,0,1,2中选取一个合适的数作为x的值代入求值.
19.如图,AD是△ABC中BC边上的中线,BF与AD相交于点E,且BE=EF,AF∥BC.
(1)求证:四边形ADCF为平行四边形;
(2)若DA=DC=3,AC=4,求△ABC的面积.
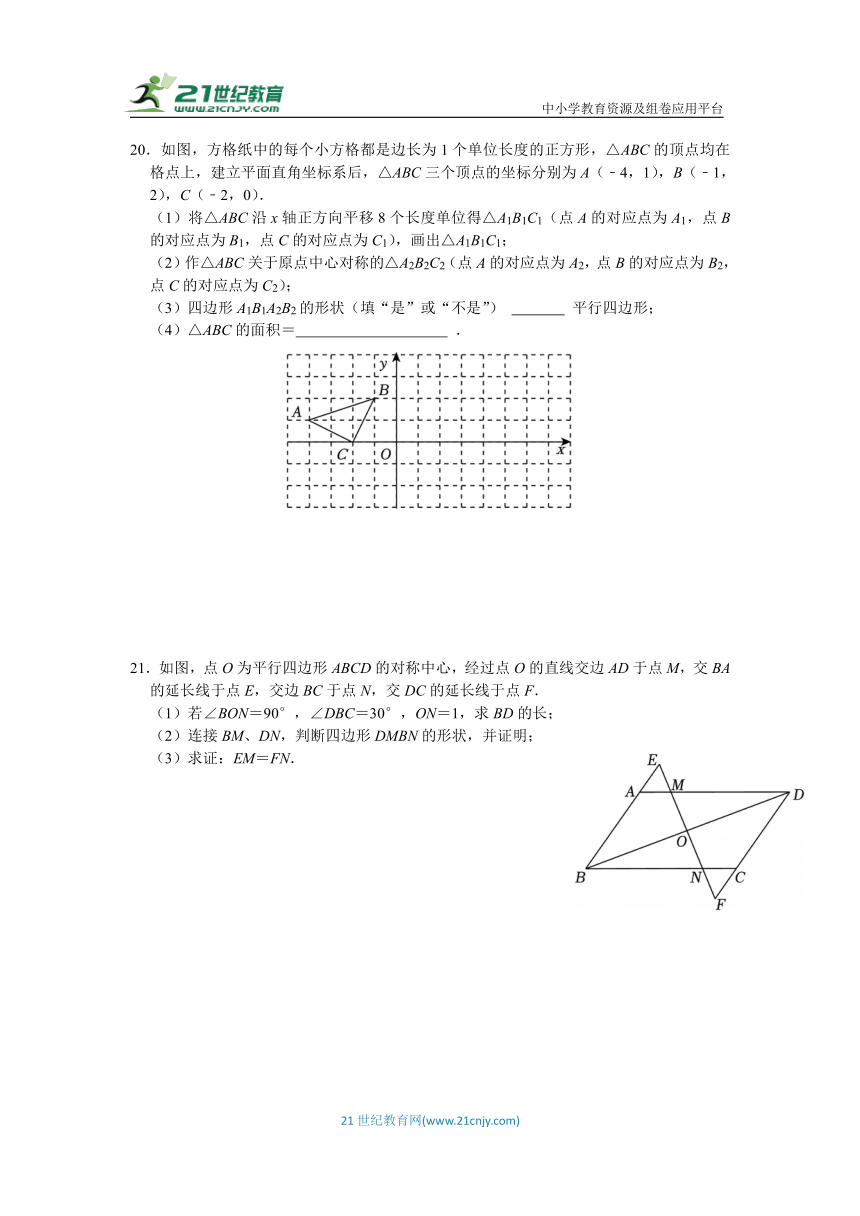
20.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(﹣4,1),B(﹣1,2),C(﹣2,0).
(1)将△ABC沿x轴正方向平移8个长度单位得△A1B1C1(点A的对应点为A1,点B的对应点为B1,点C的对应点为C1),画出△A1B1C1;
(2)作△ABC关于原点中心对称的△A2B2C2(点A的对应点为A2,点B的对应点为B2,点C的对应点为C2);
(3)四边形A1B1A2B2的形状(填“是”或“不是”) 平行四边形;
(4)△ABC的面积= .
21.如图,点O为平行四边形ABCD的对称中心,经过点O的直线交边AD于点M,交BA的延长线于点E,交边BC于点N,交DC的延长线于点F.
(1)若∠BON=90°,∠DBC=30°,ON=1,求BD的长;
(2)连接BM、DN,判断四边形DMBN的形状,并证明;
(3)求证:EM=FN.
22.在△ABC中,∠C=90°,点M是线段BC上的一点,连接AM.
(1)如图1,AC=BC,AM是△ABC的角平分线,ME⊥AB于点E.
①当CM=4时,求AB的长;
②若△ABC的中线CO交AM于点F,判断CF与ME的关系,并说明理由;
(2)如图2,若BM=AC,点N是AC上的一点,且AN=CM,连接BN交AM于点P,求∠BPM的度数.
23.《义务教育劳动课程标准》提出,将多种劳动技能纳入课程,发挥好劳动教育独特的育人价值.为让学生体验农耕劳动,某校计划购买甲、乙两种中药树苗种植.已知甲种中药树苗进价是乙种中药树苗进价的1.5倍,若用360元购进甲种中药树苗的数量比用320元购进乙种中药树苗的数量少8棵.
(1)甲、乙两种中药树苗的进价分别为每棵多少元;
(2)学校计划购买甲、乙两种中药树苗共100课,且甲树苗数量不少于乙树苗数量的3倍.请你设计一种购买树苗方案,让购买树苗的总费用最低,并求出最低费用.
24.定义:若一元一次方程的解也是一元一次不等式组的解,则称此一元一次方程为此一元一次不等式组的子方程.例如:方程4x﹣16=0的解为x=4,不等式组的解集为2<x<5,因2<4<5,故方程4x﹣16=0是不等式组的子方程.
(1)在方程①5x+2=0,②x+1=0,③x﹣(3x+1)=﹣5中,不等式组的子方程是 (填序号);
(2)若不等式组的一个子方程的解为整数,则此子方程的解是 ;
(3)若方程2x+3=x+6,2x+5(x+4)都是关于x的不等式组的子方程,求m的取值范围.
25.在平面直角坐标系xOy中,直线l1:y=﹣x+4分别与x轴,y轴相交于A,B两点,直线l2:y=kx+2k(k≠0)与x轴相交于点C,与直线l1相交于点D,连接BC.
(1)分别求点A,B,C的坐标;
(2)设△BCD的面积为S1,△ACD的面积为S2,若,求直线l2的函数表达式;
(3)以BC,CD为边作 BCDE,连接CE,交BD于点F,分别取DE的中点M,BE的中点N,连接FM,FN,当FM+FN取得最小值时,求此时 BCDE的面积.
参考答案
一、选择题
1—10:ABCAD ADADD
二、填空题
11.【解答】解:(x﹣3)(x+4)=x2+x﹣12,
所以p的数值是﹣1.
故答案为:﹣1.
12.【解答】解:∵3mx|2m﹣1|﹣7≥9是关于x的一元一次不等式,
∴|2m﹣1|=1且m≠0,
整理得,2m=2,
解得m=1,
所以m的值为1,
故答案为:1.
13.【解答】解:,
解不等式①得:x<2+a,
解不等式②得:,
∵不等式组的解集为:﹣1<x<2,
∴,
解得:a=0,b=3,
∴a﹣b=0﹣3=﹣3,
故答案为:﹣3.
14.【解答】解:设该正多边形的边数为n,根据多边形的内角和定理可得:
(n﹣2) 180°=1800°,
解得:n=12,
∴对角线为:(条),
故答案为:54.
15.【解答】解:根据平移可得DE=AB=9,DE∥AB,S△ABC=S△DEF,
∴EH=9﹣3=6,S阴影DHCF=S梯形ABEH=15,
∴(EH+AB) BE=15,
∴(6+9) BE=15,
∴BE=2,
即平移的距离为2.
故答案为:2.
16.【解答】解:过A点作AF⊥BC于F,连接AP,如图.
∵△ABC中,AB=AC=10,BC=12,
∴BF=FCBC=6,
∴△ABF中,AF8,
∵S△ABC=S△ABP+S△ACP,
∴12×810×PD10×PE,
∴4810×(PD+PE),
PD+PE.
故答案为.
三、解答题
17.【解答】解:,
解①得:x≥﹣1,
解②得:x<3.
则不等式组的解集是:﹣1≤x<3.
则整数解是:﹣1,0,1,2.
18.【解答】解:原式=()
,
∵x+1≠0,x﹣2≠0,
∴x≠﹣1,x≠2,
∴当x=0时,原式1;
当x=1时,原式3.
19.【解答】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
又∵FE=BE,∠AEF=∠DEB,
∴△AEF≌△DEB(ASA),
∴AF=DB,
∵AD是△ABC中BC边上的中线,
∴DB=DC,
∴AF=DC,
∴四边形ADCF为平行四边形;
(2)解:∵DA=DC=3,DB=DC,
∴DA=DC=DBBC,BC=6,
∴△ABC是直角三角形,且∠BAC=90°,
∴AB2,
∴S△ABCAB AC24=4.
20.【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)∵△ABC沿x轴正方向平移8个长度单位得△A1B1C1,
∴AB∥A1B1,且AB=A1B1,
∵△ABC与△A2B2C2关于原点中心对称,
∴AB∥A2B2,且AB=A2B2,
∴A1B1∥A2B2,且A1B1=A2B2,
∴四边形A1B1A2B2是平行四边形.
故答案为:是.
(4)△ABC的面积为1﹣1.
故答案为:.
21.【解答】(1)解:∵∠BON=90°,∠DBC=30°,ON=1,
∴BN=2ON=2,
∴OB,
∵点O为平行四边形ABCD的对称中心,
∴OB=OD,
∴BD=2;
(2)解:四边形DMBN是平行四边形,理由如下:
如图1,四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵OB=OD,∠DOM=∠BON,
∴△BON≌△DOM(ASA),
∴BN=DM,
∴四边形DMBN是平行四边形;
(3)证明:由(2)知:△BON≌△DOM,
∴OM=ON,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠FDO,∠E=∠F,
∵OB=OD,
∴△EBO≌△FDO(AAS),
∴OE=OF,
∴OE﹣OM=OF﹣ON,
即EM=FN.
22.【解答】解:(1)①设AC=BC=x,
∵AM是△ABC的角平分线,ME⊥AB,
则CM=ME=4,则BM=x﹣4,
在等腰直角三角形BEM中,BMME,
即x﹣4=4,则x=4+4,
则ABx=8+4;
②CF=ME且CF∥ME,理由:
如图,∵CO为直线,△ABC为等腰直角三角形,
则CO⊥AB,
而ME⊥AB,则ME∥CO,即CF∥ME,
则∠EMA=∠MFC,
由①知,EM=CM,AM=AM,
则RtAME△≌Rt△AMC(HL),
则∠EMA=∠MFC=∠EMA,
则FC=CM=EM,
即CF=ME且CF∥ME;
(2)如图,过M作ME∥AN,使ME=AN,连NE,BE,
则四边形AMEN为平行四边形,
∴NE=AM,ME⊥BC,
∵AN=MC,
∴ME=CM,
在△BEM和△AMC中,
,
∴△BEM≌△AMC(SAS),
∴BE=AM=NE,∠1=∠2,∠3=∠4,
∵∠1+∠3=90°,
∴∠2+∠4=90°且BE=NE,
∴△BEN为等腰直角三角形,∠BNE=45°,
∵AM∥NE,
∴∠BPM=∠BNE=45°.
23.【解答】解:(1)设乙种中药树苗的进价为x元,则甲种中药树苗的进价为1.5x元,
根据题意得:8,
解得:x=10,
经检验,x=10是原方程的解,且符合题意,
∴1.5x=1.5×10=15,
答:甲种中药树苗的进价为15元,乙种中药树苗的进价为10元;
(2)设购买甲种中药树苗m棵,则购买乙种中药树苗(100﹣m)棵,
根据题意得:m≥3(100﹣m),
解得:m≥75,
设购买树苗的总费用为W元,
根据题意得:W=15m+10(100﹣m)=5m+1000,
∵5>0,
∴W随m的增大而增大.
∴m=75时,W有最小值=5×75+1000=1375,
此时100﹣m=100﹣75=25,
答:购买甲种中药树苗75棵,乙种中药树苗25棵的总费用最低,最低费用是1375元.
24.【解答】解:(1)解不等式组,得:1<x<4,
∵方程①5x﹣2=0的解为x;方程②x+1=0的解为x;方程③x﹣(3x+1)=﹣5的解为x=2,
∴不等式组的子方程是是③,
故答案为:③;
(2)解不等式组得:x,
所以不等式组的整数解为﹣1,0,
则此子方程的解是﹣1或0,
故答案为:﹣1或0;
(3),
解不等式①,得:x>m,
解不等式②,得:x≤m+2,
所以不等式组的解集为m<x≤m+2.
方程2x+3=x+6的解为x=3,
方程2x+5(x+4)的解为x=2,
所以m的取值范围是1≤m<2.
25.【解答】解:(1)对于直线l:y=﹣x+4,
当x=0时,y=4,
当y=0时,﹣x+4=0,
解得x=4,
∴A(4,0),B(0,4),
对于直线 l2:y=kx+2k(k≠0),
当y=0时,kx+2k=0,
解得:x=﹣2,
∴C(﹣2,0),
故A(4,0),B(0,4),C(﹣2,0);
(2)∵,
∴S1>S2
①当点D在线段BA上时,
AC=4﹣(﹣2)=6,OB=4,
∴12,
∴S2AC×yD=3yD,
∴S1=S△ABC﹣S2=12﹣3yD,
∵,
∴,
解得yD=1,
经检验:yD=1是方程的解,
∴﹣x+4=1,
解得x=3,
∴D(3,1),
∴3k+2k=1,
解得,
∴直线l2的函数表达式为:;
②当点D在线段BA的延长线上时,
3yD,
∴S1=S△ABC+S2=12﹣3yD,
∵,
∴3,
解得yD=﹣2,
经检验yD=﹣2是方程的解,
∴﹣x+4=﹣2,
解得x=6,
∴D(6,﹣2),
∴6k+2k=﹣2,
解得,
∴直线l2的函数表达式为:;
综上所述:直线l2的函数表达式为:或;
(3)如图,作DH⊥x轴交于H,
由(1)得,
∵四边形BCDE是平行四边形,
∴CF=EF,
∵N是BE的中点,M是DE的中点,
∴,,
∴FM+FN,
∴CD取最小值时,FM+FN取得最小值,当CD⊥AB时,CD取最小值,
∵OA=OB=4,
∴∠OAB=45°,
∴,
∴∠ACD=∠CAD=45°,
∴CD=AD,
∴,
∴AH=DH=3,
∴,,
∴BD,
∴6;
∴S BCDE=2S△BDC=6;
故 BCDE的面积为6.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年八年级下册数学期末考试预测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.把5(a﹣b)+m(b﹣a)提公因式后一个因式是(a﹣b),则另一个因式是( )
A.5﹣m B.5+m C.m﹣5 D.﹣m﹣5
2.若等腰三角形的周长为16cm,其中一边长为4cm,则该等腰三角形的底边为( )
A.4cm B.6cm C.4cm或8cm D.8cm
3.下列不能判定△ABC是直角三角形的是( )
A.a2+b2﹣c2=0 B.a:b:c=3:4:5
C.∠A:∠B:∠C=3:4:5 D.∠A+∠B=∠C
4.分式的值为0,则x的值为( )
A.3 B.﹣3 C.±3 D.9
5.不等式组的解集是( )
A.x>1 B.x≤4 C.x>1或x≤4 D.1<x≤4
6.在平面直角坐标系中,点P(1,2)关于坐标原点的对称点P′的坐标为( )
A.(﹣1,﹣2) B.(﹣1,2) C.(1,﹣2) D.(1,2)
7.若ab=2,,则多项式a3b+2a2b2+ab3的值为( )
A.6 B.12 C.16 D.18
8.关于x的分式方程的解是正数,则m的取值范围是( )
A.m>2且m≠3 B.m>2 C.m≥2且m≠3 D.m≥2
9.已知△ABC的三边长a、b、c满足条件:a4﹣b4=a2c2﹣b2c2,则△ABC的形状是( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
10.如图,四边形ABCD中,∠C=∠BAD=90°,∠B=60°,若CD=2,AD=1,则四边形ABCD的面积为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.若关于x的二次三项式x2﹣px﹣12含有因式(x﹣3),则实数p的值是 .
12.若3mx|2m﹣1|﹣7≥9是关于x的一元一次不等式,则m= .
13.关于x的不等式组的解集为﹣1<x<2,则a﹣b的值为 .
14.如果一个正多边形的内角和为1800°,那么这个正多边形共有对角线 条.
15.如图,Rt△ABC和Rt△DEF重叠在一起,将△DEF沿点B到点C的方向平移到如图位置,已知AB=9.图中阴影部分的面积为15,DH=3,则平移距离为 .
16.如图:在△ABC中,AB=AC=10,BC=12,P是BC边上的动点,过点P作PD⊥AB过于点D,PE⊥AC于点E,则PD+PE的长是 .
第II卷
北师大版2024—2025学年八年级下册数学期末考试预测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解不等式组并写出它的所有的整数解.
18.先化简,然后从﹣1,0,1,2中选取一个合适的数作为x的值代入求值.
19.如图,AD是△ABC中BC边上的中线,BF与AD相交于点E,且BE=EF,AF∥BC.
(1)求证:四边形ADCF为平行四边形;
(2)若DA=DC=3,AC=4,求△ABC的面积.
20.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(﹣4,1),B(﹣1,2),C(﹣2,0).
(1)将△ABC沿x轴正方向平移8个长度单位得△A1B1C1(点A的对应点为A1,点B的对应点为B1,点C的对应点为C1),画出△A1B1C1;
(2)作△ABC关于原点中心对称的△A2B2C2(点A的对应点为A2,点B的对应点为B2,点C的对应点为C2);
(3)四边形A1B1A2B2的形状(填“是”或“不是”) 平行四边形;
(4)△ABC的面积= .
21.如图,点O为平行四边形ABCD的对称中心,经过点O的直线交边AD于点M,交BA的延长线于点E,交边BC于点N,交DC的延长线于点F.
(1)若∠BON=90°,∠DBC=30°,ON=1,求BD的长;
(2)连接BM、DN,判断四边形DMBN的形状,并证明;
(3)求证:EM=FN.
22.在△ABC中,∠C=90°,点M是线段BC上的一点,连接AM.
(1)如图1,AC=BC,AM是△ABC的角平分线,ME⊥AB于点E.
①当CM=4时,求AB的长;
②若△ABC的中线CO交AM于点F,判断CF与ME的关系,并说明理由;
(2)如图2,若BM=AC,点N是AC上的一点,且AN=CM,连接BN交AM于点P,求∠BPM的度数.
23.《义务教育劳动课程标准》提出,将多种劳动技能纳入课程,发挥好劳动教育独特的育人价值.为让学生体验农耕劳动,某校计划购买甲、乙两种中药树苗种植.已知甲种中药树苗进价是乙种中药树苗进价的1.5倍,若用360元购进甲种中药树苗的数量比用320元购进乙种中药树苗的数量少8棵.
(1)甲、乙两种中药树苗的进价分别为每棵多少元;
(2)学校计划购买甲、乙两种中药树苗共100课,且甲树苗数量不少于乙树苗数量的3倍.请你设计一种购买树苗方案,让购买树苗的总费用最低,并求出最低费用.
24.定义:若一元一次方程的解也是一元一次不等式组的解,则称此一元一次方程为此一元一次不等式组的子方程.例如:方程4x﹣16=0的解为x=4,不等式组的解集为2<x<5,因2<4<5,故方程4x﹣16=0是不等式组的子方程.
(1)在方程①5x+2=0,②x+1=0,③x﹣(3x+1)=﹣5中,不等式组的子方程是 (填序号);
(2)若不等式组的一个子方程的解为整数,则此子方程的解是 ;
(3)若方程2x+3=x+6,2x+5(x+4)都是关于x的不等式组的子方程,求m的取值范围.
25.在平面直角坐标系xOy中,直线l1:y=﹣x+4分别与x轴,y轴相交于A,B两点,直线l2:y=kx+2k(k≠0)与x轴相交于点C,与直线l1相交于点D,连接BC.
(1)分别求点A,B,C的坐标;
(2)设△BCD的面积为S1,△ACD的面积为S2,若,求直线l2的函数表达式;
(3)以BC,CD为边作 BCDE,连接CE,交BD于点F,分别取DE的中点M,BE的中点N,连接FM,FN,当FM+FN取得最小值时,求此时 BCDE的面积.
参考答案
一、选择题
1—10:ABCAD ADADD
二、填空题
11.【解答】解:(x﹣3)(x+4)=x2+x﹣12,
所以p的数值是﹣1.
故答案为:﹣1.
12.【解答】解:∵3mx|2m﹣1|﹣7≥9是关于x的一元一次不等式,
∴|2m﹣1|=1且m≠0,
整理得,2m=2,
解得m=1,
所以m的值为1,
故答案为:1.
13.【解答】解:,
解不等式①得:x<2+a,
解不等式②得:,
∵不等式组的解集为:﹣1<x<2,
∴,
解得:a=0,b=3,
∴a﹣b=0﹣3=﹣3,
故答案为:﹣3.
14.【解答】解:设该正多边形的边数为n,根据多边形的内角和定理可得:
(n﹣2) 180°=1800°,
解得:n=12,
∴对角线为:(条),
故答案为:54.
15.【解答】解:根据平移可得DE=AB=9,DE∥AB,S△ABC=S△DEF,
∴EH=9﹣3=6,S阴影DHCF=S梯形ABEH=15,
∴(EH+AB) BE=15,
∴(6+9) BE=15,
∴BE=2,
即平移的距离为2.
故答案为:2.
16.【解答】解:过A点作AF⊥BC于F,连接AP,如图.
∵△ABC中,AB=AC=10,BC=12,
∴BF=FCBC=6,
∴△ABF中,AF8,
∵S△ABC=S△ABP+S△ACP,
∴12×810×PD10×PE,
∴4810×(PD+PE),
PD+PE.
故答案为.
三、解答题
17.【解答】解:,
解①得:x≥﹣1,
解②得:x<3.
则不等式组的解集是:﹣1≤x<3.
则整数解是:﹣1,0,1,2.
18.【解答】解:原式=()
,
∵x+1≠0,x﹣2≠0,
∴x≠﹣1,x≠2,
∴当x=0时,原式1;
当x=1时,原式3.
19.【解答】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
又∵FE=BE,∠AEF=∠DEB,
∴△AEF≌△DEB(ASA),
∴AF=DB,
∵AD是△ABC中BC边上的中线,
∴DB=DC,
∴AF=DC,
∴四边形ADCF为平行四边形;
(2)解:∵DA=DC=3,DB=DC,
∴DA=DC=DBBC,BC=6,
∴△ABC是直角三角形,且∠BAC=90°,
∴AB2,
∴S△ABCAB AC24=4.
20.【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)∵△ABC沿x轴正方向平移8个长度单位得△A1B1C1,
∴AB∥A1B1,且AB=A1B1,
∵△ABC与△A2B2C2关于原点中心对称,
∴AB∥A2B2,且AB=A2B2,
∴A1B1∥A2B2,且A1B1=A2B2,
∴四边形A1B1A2B2是平行四边形.
故答案为:是.
(4)△ABC的面积为1﹣1.
故答案为:.
21.【解答】(1)解:∵∠BON=90°,∠DBC=30°,ON=1,
∴BN=2ON=2,
∴OB,
∵点O为平行四边形ABCD的对称中心,
∴OB=OD,
∴BD=2;
(2)解:四边形DMBN是平行四边形,理由如下:
如图1,四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵OB=OD,∠DOM=∠BON,
∴△BON≌△DOM(ASA),
∴BN=DM,
∴四边形DMBN是平行四边形;
(3)证明:由(2)知:△BON≌△DOM,
∴OM=ON,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠FDO,∠E=∠F,
∵OB=OD,
∴△EBO≌△FDO(AAS),
∴OE=OF,
∴OE﹣OM=OF﹣ON,
即EM=FN.
22.【解答】解:(1)①设AC=BC=x,
∵AM是△ABC的角平分线,ME⊥AB,
则CM=ME=4,则BM=x﹣4,
在等腰直角三角形BEM中,BMME,
即x﹣4=4,则x=4+4,
则ABx=8+4;
②CF=ME且CF∥ME,理由:
如图,∵CO为直线,△ABC为等腰直角三角形,
则CO⊥AB,
而ME⊥AB,则ME∥CO,即CF∥ME,
则∠EMA=∠MFC,
由①知,EM=CM,AM=AM,
则RtAME△≌Rt△AMC(HL),
则∠EMA=∠MFC=∠EMA,
则FC=CM=EM,
即CF=ME且CF∥ME;
(2)如图,过M作ME∥AN,使ME=AN,连NE,BE,
则四边形AMEN为平行四边形,
∴NE=AM,ME⊥BC,
∵AN=MC,
∴ME=CM,
在△BEM和△AMC中,
,
∴△BEM≌△AMC(SAS),
∴BE=AM=NE,∠1=∠2,∠3=∠4,
∵∠1+∠3=90°,
∴∠2+∠4=90°且BE=NE,
∴△BEN为等腰直角三角形,∠BNE=45°,
∵AM∥NE,
∴∠BPM=∠BNE=45°.
23.【解答】解:(1)设乙种中药树苗的进价为x元,则甲种中药树苗的进价为1.5x元,
根据题意得:8,
解得:x=10,
经检验,x=10是原方程的解,且符合题意,
∴1.5x=1.5×10=15,
答:甲种中药树苗的进价为15元,乙种中药树苗的进价为10元;
(2)设购买甲种中药树苗m棵,则购买乙种中药树苗(100﹣m)棵,
根据题意得:m≥3(100﹣m),
解得:m≥75,
设购买树苗的总费用为W元,
根据题意得:W=15m+10(100﹣m)=5m+1000,
∵5>0,
∴W随m的增大而增大.
∴m=75时,W有最小值=5×75+1000=1375,
此时100﹣m=100﹣75=25,
答:购买甲种中药树苗75棵,乙种中药树苗25棵的总费用最低,最低费用是1375元.
24.【解答】解:(1)解不等式组,得:1<x<4,
∵方程①5x﹣2=0的解为x;方程②x+1=0的解为x;方程③x﹣(3x+1)=﹣5的解为x=2,
∴不等式组的子方程是是③,
故答案为:③;
(2)解不等式组得:x,
所以不等式组的整数解为﹣1,0,
则此子方程的解是﹣1或0,
故答案为:﹣1或0;
(3),
解不等式①,得:x>m,
解不等式②,得:x≤m+2,
所以不等式组的解集为m<x≤m+2.
方程2x+3=x+6的解为x=3,
方程2x+5(x+4)的解为x=2,
所以m的取值范围是1≤m<2.
25.【解答】解:(1)对于直线l:y=﹣x+4,
当x=0时,y=4,
当y=0时,﹣x+4=0,
解得x=4,
∴A(4,0),B(0,4),
对于直线 l2:y=kx+2k(k≠0),
当y=0时,kx+2k=0,
解得:x=﹣2,
∴C(﹣2,0),
故A(4,0),B(0,4),C(﹣2,0);
(2)∵,
∴S1>S2
①当点D在线段BA上时,
AC=4﹣(﹣2)=6,OB=4,
∴12,
∴S2AC×yD=3yD,
∴S1=S△ABC﹣S2=12﹣3yD,
∵,
∴,
解得yD=1,
经检验:yD=1是方程的解,
∴﹣x+4=1,
解得x=3,
∴D(3,1),
∴3k+2k=1,
解得,
∴直线l2的函数表达式为:;
②当点D在线段BA的延长线上时,
3yD,
∴S1=S△ABC+S2=12﹣3yD,
∵,
∴3,
解得yD=﹣2,
经检验yD=﹣2是方程的解,
∴﹣x+4=﹣2,
解得x=6,
∴D(6,﹣2),
∴6k+2k=﹣2,
解得,
∴直线l2的函数表达式为:;
综上所述:直线l2的函数表达式为:或;
(3)如图,作DH⊥x轴交于H,
由(1)得,
∵四边形BCDE是平行四边形,
∴CF=EF,
∵N是BE的中点,M是DE的中点,
∴,,
∴FM+FN,
∴CD取最小值时,FM+FN取得最小值,当CD⊥AB时,CD取最小值,
∵OA=OB=4,
∴∠OAB=45°,
∴,
∴∠ACD=∠CAD=45°,
∴CD=AD,
∴,
∴AH=DH=3,
∴,,
∴BD,
∴6;
∴S BCDE=2S△BDC=6;
故 BCDE的面积为6.
21世纪教育网(www.21cnjy.com)
同课章节目录
