北师大版2024—2025学年八年级下学期数学期末复习训练卷
文档属性
| 名称 | 北师大版2024—2025学年八年级下学期数学期末复习训练卷 |  | |
| 格式 | docx | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 20:42:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年八年级下学期数学期末复习训练卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
2.若x>y,则下列式子错误的是( )
A.x﹣5>y﹣5 B.﹣3x>﹣3y C.x+3>y+3 D.
3.如果直角三角形的两条边长分别是3和4,则第三边的长是( )
A.7 B.5 C. D.5或
4.如图,平行四边形ABCD的两条对角线交于点E,△BEC的周长比△ABE的周长大2cm,已知AD=5cm,则AB的长为( )
A.8cm B.5cm C.3cm D.2cm
5.如图,已知AB∥CD,增加下列条件可以使四边形ABCD成为平行四边形的是( )
A.∠1=∠2 B.AD=BC C.OA=OC D.AD=AB
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=1,AB=4,则△ABD的面积是( )
A.2 B. C.3 D.
7.已知m2+n2=25,mn=12,则mn3+m3n的值为( )
A.﹣84 B.84 C.±84 D.300
8.已知△ABC的三边长a、b、c满足条件:a4﹣b4=a2c2﹣b2c2,则△ABC的形状是( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
9.如图,P是∠AOB平分线上一点,OP=10,∠AOB=120°,在绕点P旋转的过程中始终保持∠MPN=60°不变,其两边和OA,OB分别相交于M,N,下列结论:①△PMN是等边三角形;②OM+ON=10;③MN的值不变;④四边形PMON面积随着点M、N的位置的变化而变化,其中正确结论的个数为( )
A.4 B.3 C.2 D.1
10.已知关于x的不等式组下列四个结论:
①若它的解集是1<x≤2,则a=3;
②若a=2,不等式组有解;
③若它的整数解仅有3个,则a的取值范围是5≤a≤6;
④若它无解,则a≤2.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(6小题,每题3分,共18分)
11.因式分解:x3﹣x= .
12.若不等式(m﹣3)y﹣1>0(m为常数,且m≠3)的解集为,则m的取值范围是 .
13.如图,直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(m,4),则关于x的不等式﹣2x+2<kx+b的解集为 .
14.如图,在 ABCD中,AB=6,BC=8,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,则线段EF的长为 .
15.已知等腰△ABC的两边长分别为3和7,则△ABC的周长为 .
16.关于x的不等式组有且仅有3个整数解,那么m的取值范围为 .
第II卷
北师大版2024—2025学年八年级下学期数学期末复习训练卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
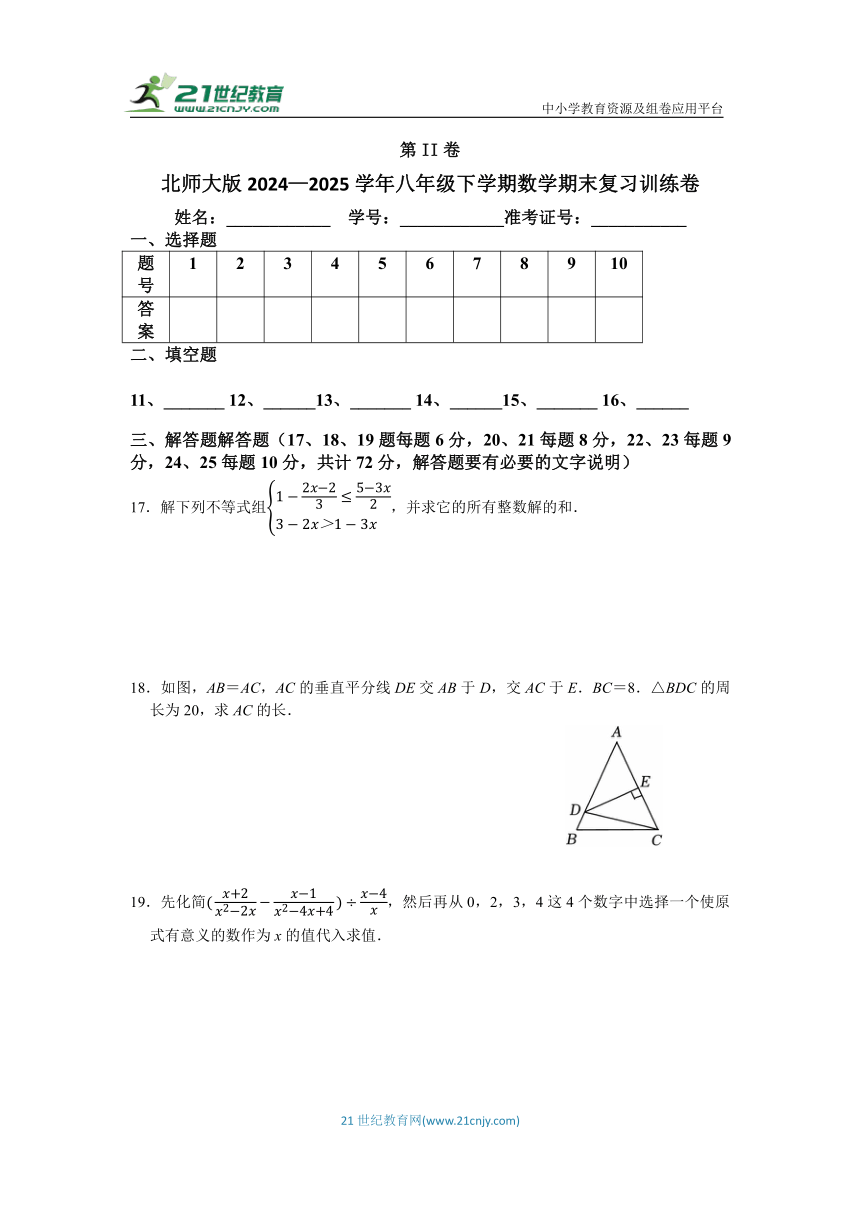
17.解下列不等式组,并求它的所有整数解的和.
18.如图,AB=AC,AC的垂直平分线DE交AB于D,交AC于E.BC=8.△BDC的周长为20,求AC的长.
19.先化简,然后再从0,2,3,4这4个数字中选择一个使原式有意义的数作为x的值代入求值.
20.解方程:
(1); (2).
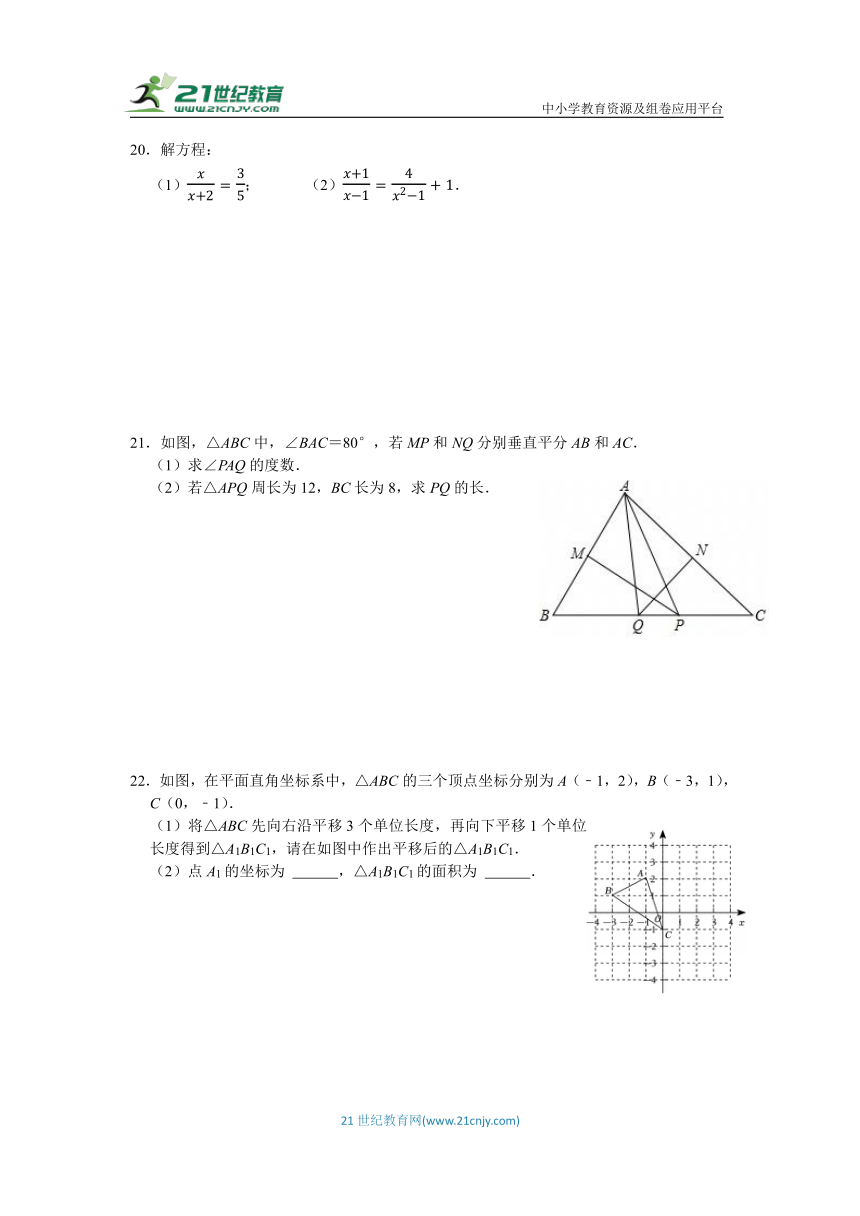
21.如图,△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数.
(2)若△APQ周长为12,BC长为8,求PQ的长.
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣1,2),B(﹣3,1),C(0,﹣1).
(1)将△ABC先向右沿平移3个单位长度,再向下平移1个单位长度得到△A1B1C1,请在如图中作出平移后的△A1B1C1.
(2)点A1的坐标为 ,△A1B1C1的面积为 .
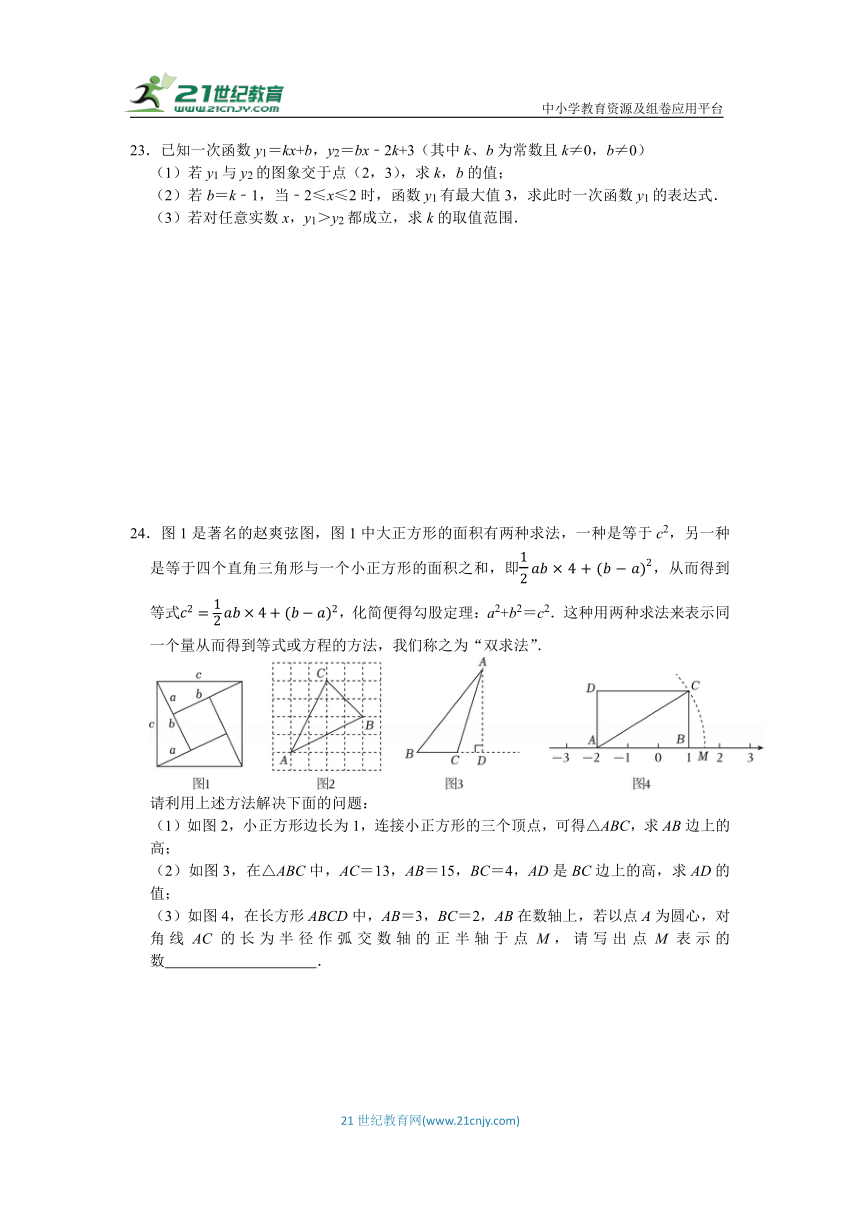
23.已知一次函数y1=kx+b,y2=bx﹣2k+3(其中k、b为常数且k≠0,b≠0)
(1)若y1与y2的图象交于点(2,3),求k,b的值;
(2)若b=k﹣1,当﹣2≤x≤2时,函数y1有最大值3,求此时一次函数y1的表达式.
(3)若对任意实数x,y1>y2都成立,求k的取值范围.
24.图1是著名的赵爽弦图,图1中大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得勾股定理:a2+b2=c2.这种用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
请利用上述方法解决下面的问题:
(1)如图2,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,求AB边上的高;
(2)如图3,在△ABC中,AC=13,AB=15,BC=4,AD是BC边上的高,求AD的值;
(3)如图4,在长方形ABCD中,AB=3,BC=2,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,请写出点M表示的数 .
25.如图,直线与x轴交于点A,直线l2:y=﹣2x+6与x轴交于点B,l1与l2交于点C.
(1)求△ABC的面积;
(2)在平面直角坐标系中是否存在一点D,使以A,B,C,D为顶点的四边形是平行四边形?若存在,请直接写出点D的坐标,若不存在,请说明理由;
(3)点P(m,0)是x轴上的动点,过点P作x轴的垂线,分别交直线l1,l2于点M,N.当PM=MN时,求m的值.
参考答案
一、选择题
1—10:CBDCC ADDCB
二、填空题
11.【解答】解:原式=x(x2﹣1)=x(x+1)(x﹣1),
故答案为:x(x+1)(x﹣1)
12.【解答】解:∵不等式(m﹣3)y﹣1>0(m为常数,且m≠3)的解集为,
∴m﹣3<0,
∴m<3.
故答案为:m<3.
13.【解答】解:∵直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(m,4),
∴4=﹣2m+2,
∴m=﹣1,
∴当x>﹣1时,﹣2x+2<kx+b,
∴不等式﹣2x+2<kx+b的解集为x>﹣1,
故答案为:x>﹣1.
14.【解答】解:∵四边形ABCD是平行四边形,
∴∠DFC=∠FCB,
又CF平分∠BCD,
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC,
同理可证:AE=AB,
∵AB=6,AD=BC=8,
∴2AB﹣BC=AE+FD﹣BC=EF=4.
故答案为:4.
15.【解答】解:由三角形三边关系可得,3为底,三角形的三边为3,7,7,可以构成三角形,周长为:3+7+7=17.
故答案为:17.
16.【解答】解:,
解不等式①得:x<m,
解不等式②得:x,
∵仅有3个整数解,
∴不等式组三个整数解为2,3,4.
∴4<m≤5.
故答案为:4<m≤5.
三、解答题
17.【解答】解:,
解①得:x≤1,
解②得:x>﹣2.
则不等式组的解集是:﹣2<x≤1,
整数解包括﹣1,0,1,
﹣1+0+1=0,
∴它的所有整数解的和为0.
18.【解答】解:∵DE垂直且平分AC,
∴AD=CD,
∴△BDC的周长=BC+BD+CD=20,
又∵BC=8,
∴AC=12.
19.【解答】解:
,
∵当x=0,2,4时,原分式无意义,
∴x=3,
当x=3时,原式.
20.【解答】解:(1),
去分母得:5x=3x+6,
解得:x=3,
检验:当x=3时,x+2≠0,
所以x=3是原方程的解;
(2),
去分母得:(x+1)2=4+x2,
解得:x=1,
检验:当x=1时,(x+1)(x﹣1)=0,
所以x=1是原方程的增根,原分式方程无解.
21.【解答】解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,
∵MP和NQ分别垂直平分AB和AC,
∴AP=PB,AQ=CQ,
∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y,
∵∠BAC=80°,
∴∠B+∠C=100°,
即x+y+z=80°,x+z+x+y=100°,
∴x=20°,
∴∠PAQ=20°;
(2)∵△APQ周长为12,
∴AQ+PQ+AP=12,
∵AQ=CQ,AP=PB,
∴CQ+PQ+PB=12,
即CQ+BQ+2PQ=12,
BC+2PQ=12,
∵BC=8,
∴PQ=2.
22.【解答】解:(1)如图,△A1B1C1即为所求作.
(2)点A1的坐标为(2,1),S△ABC=3×33×1﹣21×23×2=3.5.
故答案为:(2,1),3.5.
23.【解答】解:(1)把(2,3)代入y1,y2,得:
,解得:;
(2)若b=k﹣1,则:y1=kx+k﹣1,
①当k>0时,y随x的增大而增大,
∵﹣2≤x≤2,
∴当x=2时,y有最大值为2k+k﹣1=3,解得:;
∴;
①当k<0时,y随x的增大而减小,
∵﹣2≤x≤2,
∴当x=﹣2时,y有最大值为﹣2k+k﹣1=3,解得:k=﹣4;
∴y1=﹣4x﹣5
综上:或y1=﹣4x﹣5.
(3)由题意:两条直线平行且直线y1在直线y2的上方,
∴k=b,b>﹣2k+3,
∴k>﹣2k+3,
∴k>1.
24.【解答】解:(1)根据勾股定理可得,,
设AB边上的高为h,
∴,
∵S△ABC
=16﹣4﹣2﹣4=6,
∴,
∴;
(2)设CD=x,则BD=BC+CD=4+x,
∵AD是BC边上的高,
∴AD⊥BD,
∵AD2=AC2﹣CD2=132﹣x2,
AD2=AB2﹣BD2=152﹣(x+4)2,
∴132﹣x2=152﹣(x+4)2,
解得x=5,
∴;
(3)∵四边形ABCD是长方形,
∴∠ABC=90°,
∴,
∴AC=AM,
∵数轴上点A表示的数是﹣2,
∴点M表示的数为.
25.【解答】解:(1)对于直线 ,
令y=0,则,
解得:x=﹣2,
∴A(﹣2,0),
对于直线l2:y=﹣2x+6,
令y=0,则﹣2x+6=0,
解得:x=3,
∴B(3,0),
联立得,
解得:,
∴C(2,2);
∴;
(2)分三种情况:如图,
①以AB为对角线,BC,AC为边的平行四边形ACBD,
则AC沿CB平移可得DB,
∵C(2,2),B(3,0),
∴点C向右平移1个单位,向下平移2个单位,与点B重合.
∴点A向右平移1个单位,向下平移2个单位,得到点D,
∵A(﹣2,0),
∴D(﹣1,﹣2);
②以BC为对角线,AB,AC为边的平行四边形ABDC,
同理可得点D(7,2);
③以AC为对角线,AB,BC为边的平行四边形ABCD,
同理可得点D(﹣3,2).
综上,存在,点D的坐标为(﹣1,﹣2)或(7,2)或(﹣3,2);
(3)∵过点P作x轴的垂线,分别交直线l1,l2于点 M,N.P(m,0),
∴M、N的横坐标为m,
把x=m代入直线 ,得,
∴,
∴,
代入直线l2:y=﹣2x+6,得y=﹣2m+6,
∴N(m,﹣2m+6),
∴,
∵PM=MN,
∴,
解得:或3.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年八年级下学期数学期末复习训练卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.7,24,25 C.1.5,2,3 D.9,12,15
2.若x>y,则下列式子错误的是( )
A.x﹣5>y﹣5 B.﹣3x>﹣3y C.x+3>y+3 D.
3.如果直角三角形的两条边长分别是3和4,则第三边的长是( )
A.7 B.5 C. D.5或
4.如图,平行四边形ABCD的两条对角线交于点E,△BEC的周长比△ABE的周长大2cm,已知AD=5cm,则AB的长为( )
A.8cm B.5cm C.3cm D.2cm
5.如图,已知AB∥CD,增加下列条件可以使四边形ABCD成为平行四边形的是( )
A.∠1=∠2 B.AD=BC C.OA=OC D.AD=AB
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=1,AB=4,则△ABD的面积是( )
A.2 B. C.3 D.
7.已知m2+n2=25,mn=12,则mn3+m3n的值为( )
A.﹣84 B.84 C.±84 D.300
8.已知△ABC的三边长a、b、c满足条件:a4﹣b4=a2c2﹣b2c2,则△ABC的形状是( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
9.如图,P是∠AOB平分线上一点,OP=10,∠AOB=120°,在绕点P旋转的过程中始终保持∠MPN=60°不变,其两边和OA,OB分别相交于M,N,下列结论:①△PMN是等边三角形;②OM+ON=10;③MN的值不变;④四边形PMON面积随着点M、N的位置的变化而变化,其中正确结论的个数为( )
A.4 B.3 C.2 D.1
10.已知关于x的不等式组下列四个结论:
①若它的解集是1<x≤2,则a=3;
②若a=2,不等式组有解;
③若它的整数解仅有3个,则a的取值范围是5≤a≤6;
④若它无解,则a≤2.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(6小题,每题3分,共18分)
11.因式分解:x3﹣x= .
12.若不等式(m﹣3)y﹣1>0(m为常数,且m≠3)的解集为,则m的取值范围是 .
13.如图,直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(m,4),则关于x的不等式﹣2x+2<kx+b的解集为 .
14.如图,在 ABCD中,AB=6,BC=8,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,则线段EF的长为 .
15.已知等腰△ABC的两边长分别为3和7,则△ABC的周长为 .
16.关于x的不等式组有且仅有3个整数解,那么m的取值范围为 .
第II卷
北师大版2024—2025学年八年级下学期数学期末复习训练卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列不等式组,并求它的所有整数解的和.
18.如图,AB=AC,AC的垂直平分线DE交AB于D,交AC于E.BC=8.△BDC的周长为20,求AC的长.
19.先化简,然后再从0,2,3,4这4个数字中选择一个使原式有意义的数作为x的值代入求值.
20.解方程:
(1); (2).
21.如图,△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数.
(2)若△APQ周长为12,BC长为8,求PQ的长.
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣1,2),B(﹣3,1),C(0,﹣1).
(1)将△ABC先向右沿平移3个单位长度,再向下平移1个单位长度得到△A1B1C1,请在如图中作出平移后的△A1B1C1.
(2)点A1的坐标为 ,△A1B1C1的面积为 .
23.已知一次函数y1=kx+b,y2=bx﹣2k+3(其中k、b为常数且k≠0,b≠0)
(1)若y1与y2的图象交于点(2,3),求k,b的值;
(2)若b=k﹣1,当﹣2≤x≤2时,函数y1有最大值3,求此时一次函数y1的表达式.
(3)若对任意实数x,y1>y2都成立,求k的取值范围.
24.图1是著名的赵爽弦图,图1中大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得勾股定理:a2+b2=c2.这种用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
请利用上述方法解决下面的问题:
(1)如图2,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,求AB边上的高;
(2)如图3,在△ABC中,AC=13,AB=15,BC=4,AD是BC边上的高,求AD的值;
(3)如图4,在长方形ABCD中,AB=3,BC=2,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,请写出点M表示的数 .
25.如图,直线与x轴交于点A,直线l2:y=﹣2x+6与x轴交于点B,l1与l2交于点C.
(1)求△ABC的面积;
(2)在平面直角坐标系中是否存在一点D,使以A,B,C,D为顶点的四边形是平行四边形?若存在,请直接写出点D的坐标,若不存在,请说明理由;
(3)点P(m,0)是x轴上的动点,过点P作x轴的垂线,分别交直线l1,l2于点M,N.当PM=MN时,求m的值.
参考答案
一、选择题
1—10:CBDCC ADDCB
二、填空题
11.【解答】解:原式=x(x2﹣1)=x(x+1)(x﹣1),
故答案为:x(x+1)(x﹣1)
12.【解答】解:∵不等式(m﹣3)y﹣1>0(m为常数,且m≠3)的解集为,
∴m﹣3<0,
∴m<3.
故答案为:m<3.
13.【解答】解:∵直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(m,4),
∴4=﹣2m+2,
∴m=﹣1,
∴当x>﹣1时,﹣2x+2<kx+b,
∴不等式﹣2x+2<kx+b的解集为x>﹣1,
故答案为:x>﹣1.
14.【解答】解:∵四边形ABCD是平行四边形,
∴∠DFC=∠FCB,
又CF平分∠BCD,
∴∠DCF=∠FCB,
∴∠DFC=∠DCF,
∴DF=DC,
同理可证:AE=AB,
∵AB=6,AD=BC=8,
∴2AB﹣BC=AE+FD﹣BC=EF=4.
故答案为:4.
15.【解答】解:由三角形三边关系可得,3为底,三角形的三边为3,7,7,可以构成三角形,周长为:3+7+7=17.
故答案为:17.
16.【解答】解:,
解不等式①得:x<m,
解不等式②得:x,
∵仅有3个整数解,
∴不等式组三个整数解为2,3,4.
∴4<m≤5.
故答案为:4<m≤5.
三、解答题
17.【解答】解:,
解①得:x≤1,
解②得:x>﹣2.
则不等式组的解集是:﹣2<x≤1,
整数解包括﹣1,0,1,
﹣1+0+1=0,
∴它的所有整数解的和为0.
18.【解答】解:∵DE垂直且平分AC,
∴AD=CD,
∴△BDC的周长=BC+BD+CD=20,
又∵BC=8,
∴AC=12.
19.【解答】解:
,
∵当x=0,2,4时,原分式无意义,
∴x=3,
当x=3时,原式.
20.【解答】解:(1),
去分母得:5x=3x+6,
解得:x=3,
检验:当x=3时,x+2≠0,
所以x=3是原方程的解;
(2),
去分母得:(x+1)2=4+x2,
解得:x=1,
检验:当x=1时,(x+1)(x﹣1)=0,
所以x=1是原方程的增根,原分式方程无解.
21.【解答】解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,
∵MP和NQ分别垂直平分AB和AC,
∴AP=PB,AQ=CQ,
∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y,
∵∠BAC=80°,
∴∠B+∠C=100°,
即x+y+z=80°,x+z+x+y=100°,
∴x=20°,
∴∠PAQ=20°;
(2)∵△APQ周长为12,
∴AQ+PQ+AP=12,
∵AQ=CQ,AP=PB,
∴CQ+PQ+PB=12,
即CQ+BQ+2PQ=12,
BC+2PQ=12,
∵BC=8,
∴PQ=2.
22.【解答】解:(1)如图,△A1B1C1即为所求作.
(2)点A1的坐标为(2,1),S△ABC=3×33×1﹣21×23×2=3.5.
故答案为:(2,1),3.5.
23.【解答】解:(1)把(2,3)代入y1,y2,得:
,解得:;
(2)若b=k﹣1,则:y1=kx+k﹣1,
①当k>0时,y随x的增大而增大,
∵﹣2≤x≤2,
∴当x=2时,y有最大值为2k+k﹣1=3,解得:;
∴;
①当k<0时,y随x的增大而减小,
∵﹣2≤x≤2,
∴当x=﹣2时,y有最大值为﹣2k+k﹣1=3,解得:k=﹣4;
∴y1=﹣4x﹣5
综上:或y1=﹣4x﹣5.
(3)由题意:两条直线平行且直线y1在直线y2的上方,
∴k=b,b>﹣2k+3,
∴k>﹣2k+3,
∴k>1.
24.【解答】解:(1)根据勾股定理可得,,
设AB边上的高为h,
∴,
∵S△ABC
=16﹣4﹣2﹣4=6,
∴,
∴;
(2)设CD=x,则BD=BC+CD=4+x,
∵AD是BC边上的高,
∴AD⊥BD,
∵AD2=AC2﹣CD2=132﹣x2,
AD2=AB2﹣BD2=152﹣(x+4)2,
∴132﹣x2=152﹣(x+4)2,
解得x=5,
∴;
(3)∵四边形ABCD是长方形,
∴∠ABC=90°,
∴,
∴AC=AM,
∵数轴上点A表示的数是﹣2,
∴点M表示的数为.
25.【解答】解:(1)对于直线 ,
令y=0,则,
解得:x=﹣2,
∴A(﹣2,0),
对于直线l2:y=﹣2x+6,
令y=0,则﹣2x+6=0,
解得:x=3,
∴B(3,0),
联立得,
解得:,
∴C(2,2);
∴;
(2)分三种情况:如图,
①以AB为对角线,BC,AC为边的平行四边形ACBD,
则AC沿CB平移可得DB,
∵C(2,2),B(3,0),
∴点C向右平移1个单位,向下平移2个单位,与点B重合.
∴点A向右平移1个单位,向下平移2个单位,得到点D,
∵A(﹣2,0),
∴D(﹣1,﹣2);
②以BC为对角线,AB,AC为边的平行四边形ABDC,
同理可得点D(7,2);
③以AC为对角线,AB,BC为边的平行四边形ABCD,
同理可得点D(﹣3,2).
综上,存在,点D的坐标为(﹣1,﹣2)或(7,2)或(﹣3,2);
(3)∵过点P作x轴的垂线,分别交直线l1,l2于点 M,N.P(m,0),
∴M、N的横坐标为m,
把x=m代入直线 ,得,
∴,
∴,
代入直线l2:y=﹣2x+6,得y=﹣2m+6,
∴N(m,﹣2m+6),
∴,
∵PM=MN,
∴,
解得:或3.
21世纪教育网(www.21cnjy.com)
同课章节目录
