北师大版2024—2025学年八年级下册数学期末考试调研检测卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年八年级下册数学期末考试调研检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 874.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 20:39:53 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年八年级下册数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,是中心对称的图形是( )
A. B. C. D.
2.三角形的三边长分别为a、b、c,且满足等式:(a+b)2﹣c2=2ab,则此三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.等腰三角形
3.已知关于x的不等式>1的解都是不等式>0的解,则a的范围是( )
A.a=5 B.a≥5 C.a≤5 D.a<5
4.如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
5.如图,在△ABC中,DE,FG分别是线段AB,BC的垂直平分线,若∠ABC=100°,则∠DBF的度数是( )
A.20° B.30° C.40° D.50°
6.如图,OP平分∠AOB,PC⊥OA于点C,点D在OB上,若PC=3,OD=6,则△POD的面积为( )
A.3 B.6 C.9 D.18
7.用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45° B.每一个内角都小于45°
C.有一个内角大于等于45° D.每一个内角都大于等于45°
8.△ABC中,AB=13,AC=15,高AD=12,则BC的长为( )
A.14 B.4 C.14或4 D.以上都不对
9.关于x的分式方程的解是正数,则m的取值范围是( )
A.m>2且m≠3 B.m>2 C.m≥2且m≠3 D.m≥2
10.已知关于x的不等式组恰有3个整数解,则a的取值范围是( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.分解因式:ma2﹣2ma+m= .
12.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
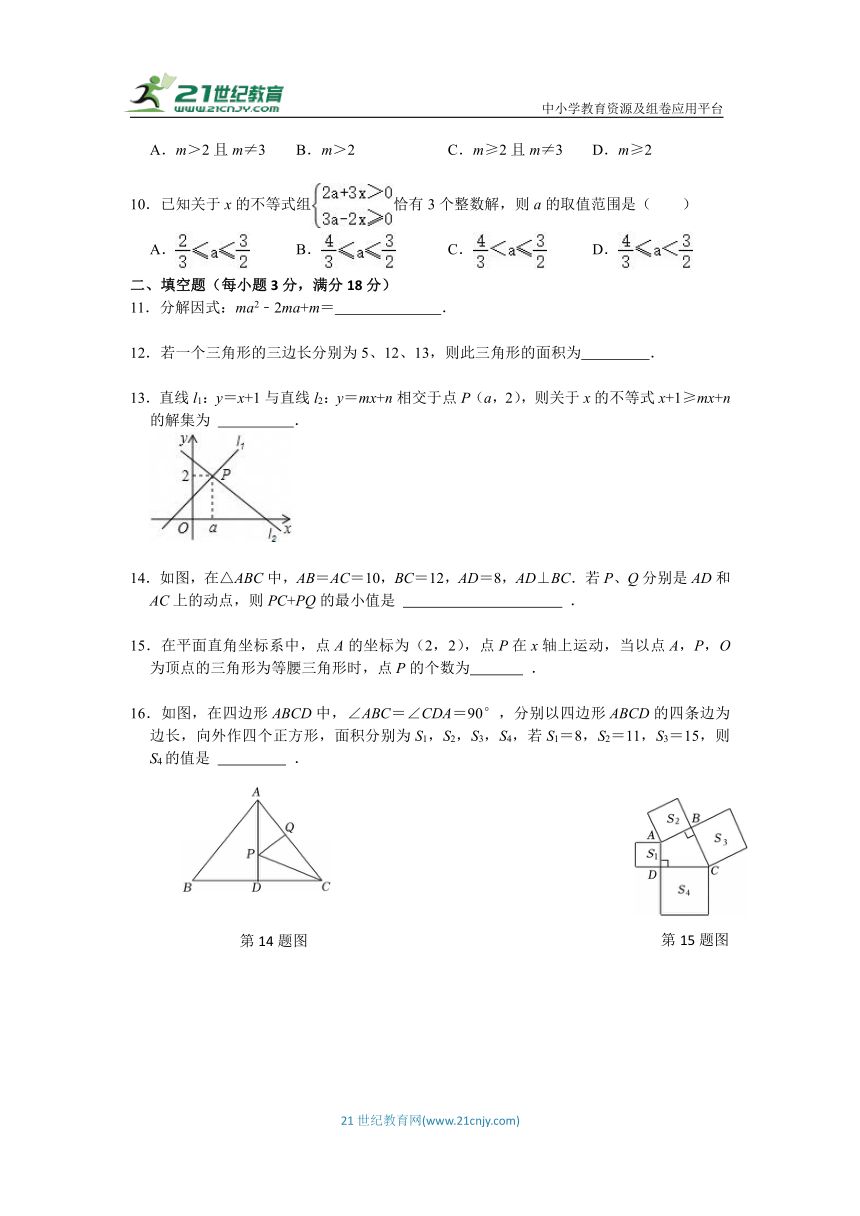
13.直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
14.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是 .
15.在平面直角坐标系中,点A的坐标为(2,2),点P在x轴上运动,当以点A,P,O为顶点的三角形为等腰三角形时,点P的个数为 .
16.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=8,S2=11,S3=15,则S4的值是 .
第II卷
北师大版2024—2025学年八年级下册数学期末考试调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
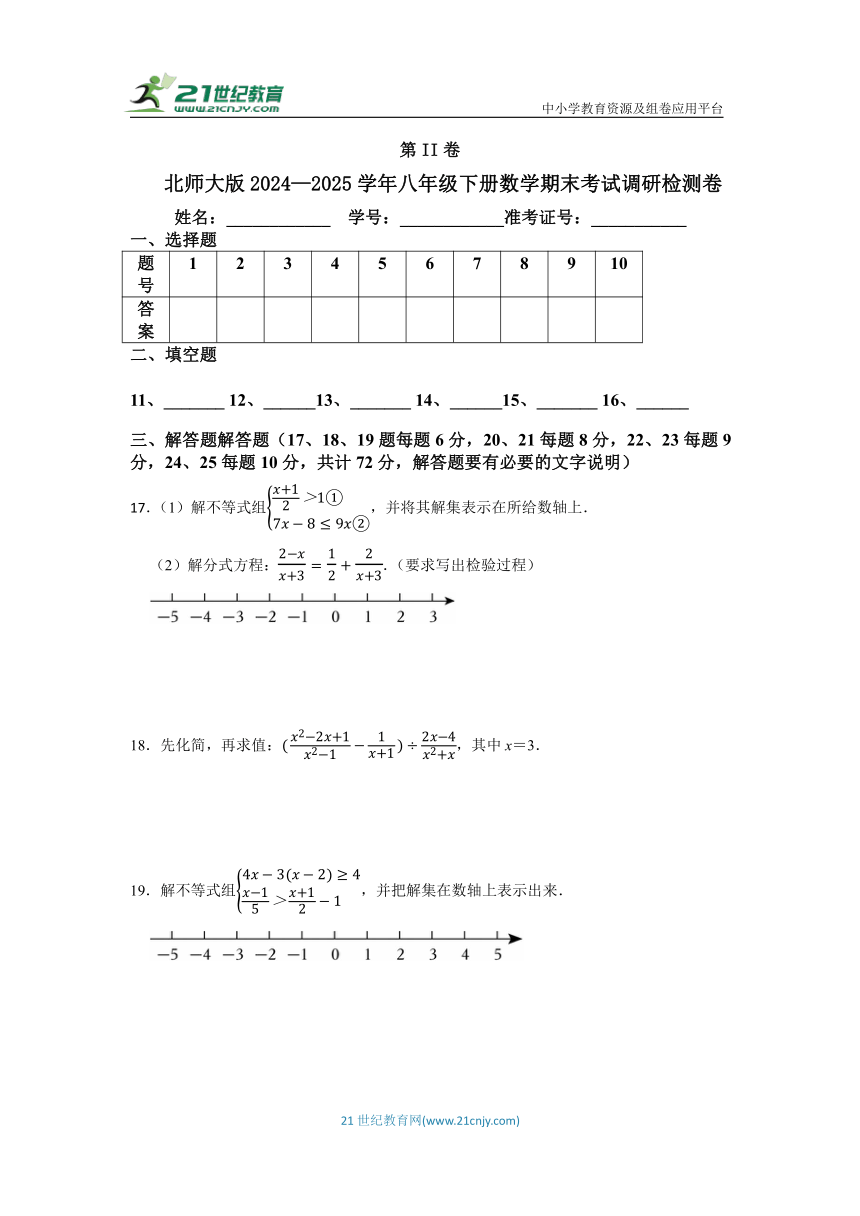
17.(1)解不等式组,并将其解集表示在所给数轴上.
(2)解分式方程:.(要求写出检验过程)
18.先化简,再求值:,其中x=3.
19.解不等式组,并把解集在数轴上表示出来.
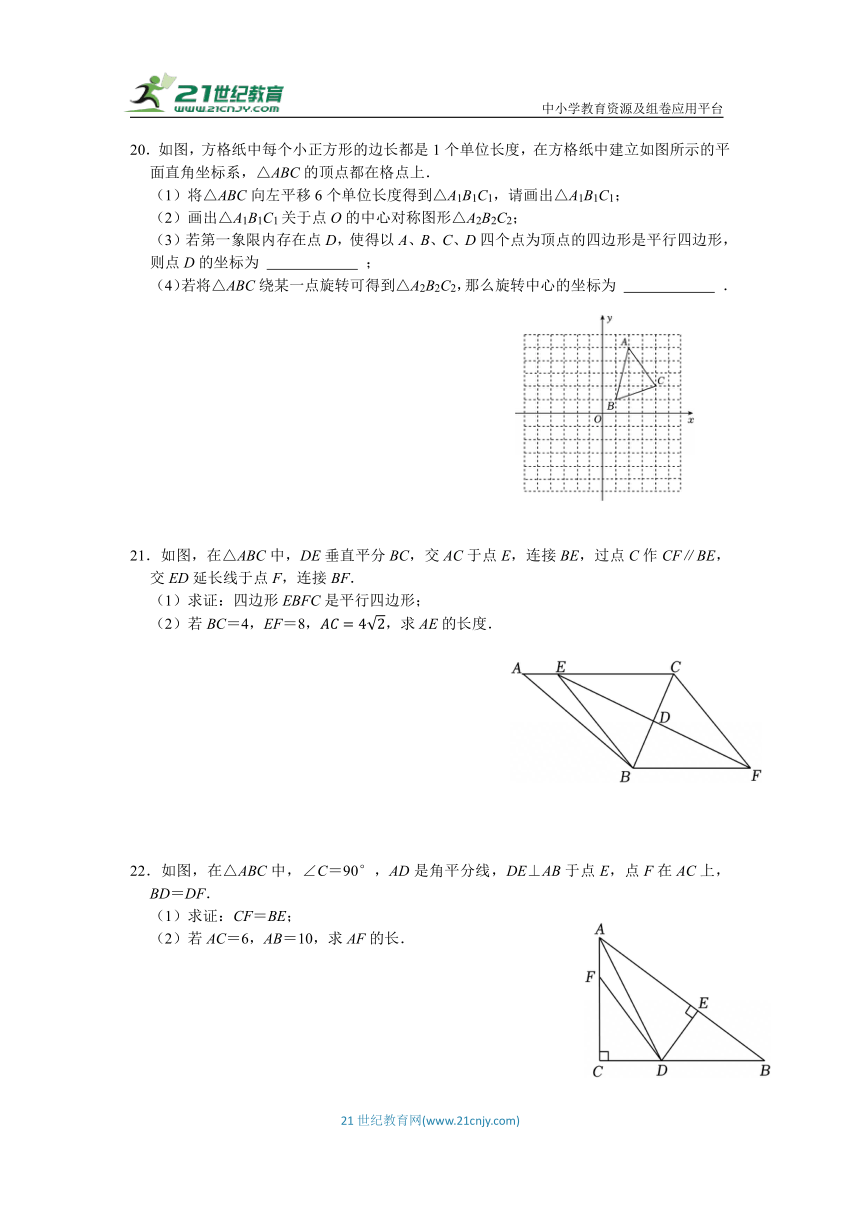
20.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向左平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若第一象限内存在点D,使得以A、B、C、D四个点为顶点的四边形是平行四边形,则点D的坐标为 ;
(4)若将△ABC绕某一点旋转可得到△A2B2C2,那么旋转中心的坐标为 .
21.如图,在△ABC中,DE垂直平分BC,交AC于点E,连接BE,过点C作CF∥BE,交ED延长线于点F,连接BF.
(1)求证:四边形EBFC是平行四边形;
(2)若BC=4,EF=8,,求AE的长度.
22.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=BE;
(2)若AC=6,AB=10,求AF的长.
23.定义:若一元一次方程的解也是一元一次不等式组的解,则称此一元一次方程为此一元一次不等式组的子方程.例如:方程4x﹣16=0的解为x=4,不等式组的解集为2<x<5,因2<4<5,故方程4x﹣16=0是不等式组的子方程.
(1)在方程①5x+2=0,②x+1=0,③x﹣(3x+1)=﹣5中,不等式组的子方程是 (填序号);
(2)若不等式组的一个子方程的解为整数,则此子方程的解是 ;
(3)若方程2x+3=x+6,2x+5(x+4)都是关于x的不等式组的子方程,求m的取值范围.
24.如图,在平面直角坐标系xOy中,直线y=kx+b与x轴、y轴分别交于A,B两点,∠OAB=45°,点A的坐标为(4,0).点C(m,n)是线段AB上一点,连接OC并延长至D,使DC=OC,连接BD.
(1)求直线AB的表达式;
(2)若△BCD是直角三角形,求点C的坐标;
(3)若直线y=mx+2n﹣18与△BCD的边有两个交点,求m的取值范围.
25.在平面直角坐标系xOy中,直线l1:y=﹣x+4分别与x轴,y轴相交于A,B两点,直线l2:y=kx+2k(k≠0)与x轴相交于点C,与直线l1相交于点D,连接BC.
(1)分别求点A,B,C的坐标;
(2)设△BCD的面积为S1,△ACD的面积为S2,若,求直线l2的函数表达式;
(3)以BC,CD为边作 BCDE,连接CE,交BD于点F,分别取DE的中点M,BE的中点N,连接FM,FN,当FM+FN取得最小值时,求此时 BCDE的面积.
参考答案
一、选择题
1—10:BCCDA CDCAB
二、填空题
11.【解答】解:ma2﹣2ma+m
=m(a2﹣2a+1)
=m(a﹣1)2,
故答案为:m(a﹣1)2.
12.【解答】解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为5×12=30.
13.【解答】解:将点P(a,2)坐标代入直线y=x+1,得a=1,
从图中直接看出,当x≥1时,x+1≥mx+n,
故答案为:x≥1.
14.【解答】解:如图,连接BP,
在△ABC中,AB=AC=10,BC=12,AD=8,
∴BD=DC,
∴BP=PC,
∴PC+PQ=BP+PQ=BQ,
∴当B,P,Q共线时,PC+PQ的值最小,
∴当BQ⊥AC时,BQ的值最小,
令AQ'=a,则CQ'=10﹣a,
∵BQ'⊥AC,
∴AB2﹣AQ'2=BC2﹣CQ'2,
即102﹣a2=122﹣(10﹣a)2,
解得a,
∴BQ',
∴PC+PQ的最小值为,
故答案为:.
15.【解答】解:如图:
如图,当OA=OP时,可得P1、P2满足条件;
当PA=PO时,可得P3满足条件;
当AO=AP时,可得P4满足条件.
满足条件的点P有四个.
故答案为:4.
16.【解答】解:如图,连接AC,
∵S1=8,S2=11,S3=15,
∴AD2=8,AB2=11,BC2=15,
在Rt△ABC与Rt△ADC中,由勾股定理得,
AC2=AB2+BC2=26,
∴CD2=AC2﹣AD2,
∴CD2=26﹣8=18,
∴S4=18,
故答案为:18.
三、解答题
17.【解答】解:(1)解不等式①得:x>1,
解不等式②得:x≥﹣4,
故原不等式组的解集为x>1,
将其解集在数轴上表示如图所示:
;
(2)原方程去分母得:4﹣2x=x+3+4,
解得:x=﹣1,
检验:当x=﹣1时,2(x+3)≠0,
故原方程的解为x=﹣1.
18.【解答】解:
=[]
=()
,
当x=3时,原式.
19.【解答】解:解不等式①,得:x≥﹣2,
解不等式②,得:x<1,
则不等式组的解集为﹣2≤x<1,
将不等式组的解集表示在数轴上如下:
20.【解答】解:(1)如图1,△A1B1C1即为所求.
(2)如图1,△A2B2C2即为所求.
(3)如图2,
故点D的坐标为(5,6);
(4)如图1,连接AA2,BB2,CC2,交于点M,
则△ABC绕点M旋转180°可得到△A2B2C2,
∴旋转中心M的坐标为(3,0).
故答案为:(3,0).
21.【解答】(1)证明:∵DE垂直平分BC,
∴DB=DC,
∵CF∥BE,
∴∠BED=∠CFD,∠EBD=∠FCD,
∴△EBD≌△FCD(AAS),
∴BE=CF,
∴四边形EBFC是平行四边形;
(2)解:由(1)可知,四边形EBFC是平行四边形,
∴DCBC=2,DE=DFEF=4,
∵DE垂直平分BC,
∴∠CDE=90°,
∴CE2,
∴AE=AC﹣CE=42,
即AE的长为42.
22.【解答】(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,∠BED=∠C=90°.
在Rt△CDF和Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=BE.
(2)在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵AC=6,AB=10,
∴BE=AB﹣AE=AB﹣AC=4.
∴AF=AC﹣CF=AC﹣BE=2.
23.【解答】解:(1)解不等式组,得:1<x<4,
∵方程①5x﹣2=0的解为x;方程②x+1=0的解为x;方程③x﹣(3x+1)=﹣5的解为x=2,
∴不等式组的子方程是是③,
故答案为:③;
(2)解不等式组得:x,
所以不等式组的整数解为﹣1,0,
则此子方程的解是﹣1或0,
故答案为:﹣1或0;
(3),
解不等式①,得:x>m,
解不等式②,得:x≤m+2,
所以不等式组的解集为m<x≤m+2.
方程2x+3=x+6的解为x=3,
方程2x+5(x+4)的解为x=2,
所以m的取值范围是1≤m<2.
24.【解答】解:(1)∵∠OAB=45°,点A的坐标为(4,0),则点B(0,4),即b=4,
则AB的表达式为:y=kx+4,
将点A的坐标代入上式得:0=4k+4,则k=﹣1,
故直线AB的表达式为:y=﹣x+4;
(2)设点C(m,﹣m+4),
∵DC=OC,则点D(2m,8﹣2m),
由B、C、D的坐标得,CD2=2m2﹣8m+16,BD2=8m2﹣16m+16,BC2=2m2,
当CD为斜边时,
则2m2﹣8m+16=8m2﹣16m+16+2m2,
解得:m=0(舍去)或1,即点C(1,3);
当BD或BC为斜边时,
同理可得:8m2﹣16m+16=2m2+2m2﹣8m+16或2m2﹣8m+16+8m2﹣16m+16=2m2,
解得:m=0(舍去)或2,即点C(2,2);
综上,点C(1,3)或(2,2);
(3)∵点C(m,n)是线段AB上一点,直线AB的表达式为y=﹣x+4,
∴n=﹣m+4,0≤m≤4,
∴y=mx+2n﹣18=m(x﹣2)﹣10,即直线过点(2,﹣10),
∵由(2)可知C是OD的中点,
∴D点坐标为(2m,2n),
∴D点坐标为(2m,8﹣2m),代入函数表达式得:8﹣2m=m (2m)+2(﹣m+4)﹣18,
解得:m=﹣3(舍去)或3,
∵0≤m≤4,
∴3<m≤4.
25.【解答】解:(1)对于直线l:y=﹣x+4,
当x=0时,y=4,
当y=0时,﹣x+4=0,
解得x=4,
∴A(4,0),B(0,4),
对于直线 l2:y=kx+2k(k≠0),
当y=0时,kx+2k=0,
解得:x=﹣2,
∴C(﹣2,0),
故A(4,0),B(0,4),C(﹣2,0);
(2)∵,
∴S1>S2
①当点D在线段BA上时,
AC=4﹣(﹣2)=6,OB=4,
∴12,
∴S2AC×yD=3yD,
∴S1=S△ABC﹣S2=12﹣3yD,
∵,
∴,
解得yD=1,
经检验:yD=1是方程的解,
∴﹣x+4=1,
解得x=3,
∴D(3,1),
∴3k+2k=1,
解得,
∴直线l2的函数表达式为:;
②当点D在线段BA的延长线上时,
3yD,
∴S1=S△ABC+S2=12﹣3yD,
∵,
∴3,
解得yD=﹣2,
经检验yD=﹣2是方程的解,
∴﹣x+4=﹣2,
解得x=6,
∴D(6,﹣2),
∴6k+2k=﹣2,
解得,
∴直线l2的函数表达式为:;
综上所述:直线l2的函数表达式为:或;
(3)如图,作DH⊥x轴交于H,
由(1)得,
∵四边形BCDE是平行四边形,
∴CF=EF,
∵N是BE的中点,M是DE的中点,
∴,,
∴FM+FN,
∴CD取最小值时,FM+FN取得最小值,当CD⊥AB时,CD取最小值,
∵OA=OB=4,
∴∠OAB=45°,
∴,
∴∠ACD=∠CAD=45°,
∴CD=AD,
∴,
∴AH=DH=3,
∴,,
∴BD,
∴6;
∴S BCDE=2S△BDC=6;
故 BCDE的面积为6.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年八年级下册数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,是中心对称的图形是( )
A. B. C. D.
2.三角形的三边长分别为a、b、c,且满足等式:(a+b)2﹣c2=2ab,则此三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.等腰三角形
3.已知关于x的不等式>1的解都是不等式>0的解,则a的范围是( )
A.a=5 B.a≥5 C.a≤5 D.a<5
4.如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
5.如图,在△ABC中,DE,FG分别是线段AB,BC的垂直平分线,若∠ABC=100°,则∠DBF的度数是( )
A.20° B.30° C.40° D.50°
6.如图,OP平分∠AOB,PC⊥OA于点C,点D在OB上,若PC=3,OD=6,则△POD的面积为( )
A.3 B.6 C.9 D.18
7.用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45° B.每一个内角都小于45°
C.有一个内角大于等于45° D.每一个内角都大于等于45°
8.△ABC中,AB=13,AC=15,高AD=12,则BC的长为( )
A.14 B.4 C.14或4 D.以上都不对
9.关于x的分式方程的解是正数,则m的取值范围是( )
A.m>2且m≠3 B.m>2 C.m≥2且m≠3 D.m≥2
10.已知关于x的不等式组恰有3个整数解,则a的取值范围是( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.分解因式:ma2﹣2ma+m= .
12.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
13.直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
14.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是 .
15.在平面直角坐标系中,点A的坐标为(2,2),点P在x轴上运动,当以点A,P,O为顶点的三角形为等腰三角形时,点P的个数为 .
16.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=8,S2=11,S3=15,则S4的值是 .
第II卷
北师大版2024—2025学年八年级下册数学期末考试调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)解不等式组,并将其解集表示在所给数轴上.
(2)解分式方程:.(要求写出检验过程)
18.先化简,再求值:,其中x=3.
19.解不等式组,并把解集在数轴上表示出来.
20.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向左平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若第一象限内存在点D,使得以A、B、C、D四个点为顶点的四边形是平行四边形,则点D的坐标为 ;
(4)若将△ABC绕某一点旋转可得到△A2B2C2,那么旋转中心的坐标为 .
21.如图,在△ABC中,DE垂直平分BC,交AC于点E,连接BE,过点C作CF∥BE,交ED延长线于点F,连接BF.
(1)求证:四边形EBFC是平行四边形;
(2)若BC=4,EF=8,,求AE的长度.
22.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=BE;
(2)若AC=6,AB=10,求AF的长.
23.定义:若一元一次方程的解也是一元一次不等式组的解,则称此一元一次方程为此一元一次不等式组的子方程.例如:方程4x﹣16=0的解为x=4,不等式组的解集为2<x<5,因2<4<5,故方程4x﹣16=0是不等式组的子方程.
(1)在方程①5x+2=0,②x+1=0,③x﹣(3x+1)=﹣5中,不等式组的子方程是 (填序号);
(2)若不等式组的一个子方程的解为整数,则此子方程的解是 ;
(3)若方程2x+3=x+6,2x+5(x+4)都是关于x的不等式组的子方程,求m的取值范围.
24.如图,在平面直角坐标系xOy中,直线y=kx+b与x轴、y轴分别交于A,B两点,∠OAB=45°,点A的坐标为(4,0).点C(m,n)是线段AB上一点,连接OC并延长至D,使DC=OC,连接BD.
(1)求直线AB的表达式;
(2)若△BCD是直角三角形,求点C的坐标;
(3)若直线y=mx+2n﹣18与△BCD的边有两个交点,求m的取值范围.
25.在平面直角坐标系xOy中,直线l1:y=﹣x+4分别与x轴,y轴相交于A,B两点,直线l2:y=kx+2k(k≠0)与x轴相交于点C,与直线l1相交于点D,连接BC.
(1)分别求点A,B,C的坐标;
(2)设△BCD的面积为S1,△ACD的面积为S2,若,求直线l2的函数表达式;
(3)以BC,CD为边作 BCDE,连接CE,交BD于点F,分别取DE的中点M,BE的中点N,连接FM,FN,当FM+FN取得最小值时,求此时 BCDE的面积.
参考答案
一、选择题
1—10:BCCDA CDCAB
二、填空题
11.【解答】解:ma2﹣2ma+m
=m(a2﹣2a+1)
=m(a﹣1)2,
故答案为:m(a﹣1)2.
12.【解答】解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为5×12=30.
13.【解答】解:将点P(a,2)坐标代入直线y=x+1,得a=1,
从图中直接看出,当x≥1时,x+1≥mx+n,
故答案为:x≥1.
14.【解答】解:如图,连接BP,
在△ABC中,AB=AC=10,BC=12,AD=8,
∴BD=DC,
∴BP=PC,
∴PC+PQ=BP+PQ=BQ,
∴当B,P,Q共线时,PC+PQ的值最小,
∴当BQ⊥AC时,BQ的值最小,
令AQ'=a,则CQ'=10﹣a,
∵BQ'⊥AC,
∴AB2﹣AQ'2=BC2﹣CQ'2,
即102﹣a2=122﹣(10﹣a)2,
解得a,
∴BQ',
∴PC+PQ的最小值为,
故答案为:.
15.【解答】解:如图:
如图,当OA=OP时,可得P1、P2满足条件;
当PA=PO时,可得P3满足条件;
当AO=AP时,可得P4满足条件.
满足条件的点P有四个.
故答案为:4.
16.【解答】解:如图,连接AC,
∵S1=8,S2=11,S3=15,
∴AD2=8,AB2=11,BC2=15,
在Rt△ABC与Rt△ADC中,由勾股定理得,
AC2=AB2+BC2=26,
∴CD2=AC2﹣AD2,
∴CD2=26﹣8=18,
∴S4=18,
故答案为:18.
三、解答题
17.【解答】解:(1)解不等式①得:x>1,
解不等式②得:x≥﹣4,
故原不等式组的解集为x>1,
将其解集在数轴上表示如图所示:
;
(2)原方程去分母得:4﹣2x=x+3+4,
解得:x=﹣1,
检验:当x=﹣1时,2(x+3)≠0,
故原方程的解为x=﹣1.
18.【解答】解:
=[]
=()
,
当x=3时,原式.
19.【解答】解:解不等式①,得:x≥﹣2,
解不等式②,得:x<1,
则不等式组的解集为﹣2≤x<1,
将不等式组的解集表示在数轴上如下:
20.【解答】解:(1)如图1,△A1B1C1即为所求.
(2)如图1,△A2B2C2即为所求.
(3)如图2,
故点D的坐标为(5,6);
(4)如图1,连接AA2,BB2,CC2,交于点M,
则△ABC绕点M旋转180°可得到△A2B2C2,
∴旋转中心M的坐标为(3,0).
故答案为:(3,0).
21.【解答】(1)证明:∵DE垂直平分BC,
∴DB=DC,
∵CF∥BE,
∴∠BED=∠CFD,∠EBD=∠FCD,
∴△EBD≌△FCD(AAS),
∴BE=CF,
∴四边形EBFC是平行四边形;
(2)解:由(1)可知,四边形EBFC是平行四边形,
∴DCBC=2,DE=DFEF=4,
∵DE垂直平分BC,
∴∠CDE=90°,
∴CE2,
∴AE=AC﹣CE=42,
即AE的长为42.
22.【解答】(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,∠BED=∠C=90°.
在Rt△CDF和Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=BE.
(2)在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵AC=6,AB=10,
∴BE=AB﹣AE=AB﹣AC=4.
∴AF=AC﹣CF=AC﹣BE=2.
23.【解答】解:(1)解不等式组,得:1<x<4,
∵方程①5x﹣2=0的解为x;方程②x+1=0的解为x;方程③x﹣(3x+1)=﹣5的解为x=2,
∴不等式组的子方程是是③,
故答案为:③;
(2)解不等式组得:x,
所以不等式组的整数解为﹣1,0,
则此子方程的解是﹣1或0,
故答案为:﹣1或0;
(3),
解不等式①,得:x>m,
解不等式②,得:x≤m+2,
所以不等式组的解集为m<x≤m+2.
方程2x+3=x+6的解为x=3,
方程2x+5(x+4)的解为x=2,
所以m的取值范围是1≤m<2.
24.【解答】解:(1)∵∠OAB=45°,点A的坐标为(4,0),则点B(0,4),即b=4,
则AB的表达式为:y=kx+4,
将点A的坐标代入上式得:0=4k+4,则k=﹣1,
故直线AB的表达式为:y=﹣x+4;
(2)设点C(m,﹣m+4),
∵DC=OC,则点D(2m,8﹣2m),
由B、C、D的坐标得,CD2=2m2﹣8m+16,BD2=8m2﹣16m+16,BC2=2m2,
当CD为斜边时,
则2m2﹣8m+16=8m2﹣16m+16+2m2,
解得:m=0(舍去)或1,即点C(1,3);
当BD或BC为斜边时,
同理可得:8m2﹣16m+16=2m2+2m2﹣8m+16或2m2﹣8m+16+8m2﹣16m+16=2m2,
解得:m=0(舍去)或2,即点C(2,2);
综上,点C(1,3)或(2,2);
(3)∵点C(m,n)是线段AB上一点,直线AB的表达式为y=﹣x+4,
∴n=﹣m+4,0≤m≤4,
∴y=mx+2n﹣18=m(x﹣2)﹣10,即直线过点(2,﹣10),
∵由(2)可知C是OD的中点,
∴D点坐标为(2m,2n),
∴D点坐标为(2m,8﹣2m),代入函数表达式得:8﹣2m=m (2m)+2(﹣m+4)﹣18,
解得:m=﹣3(舍去)或3,
∵0≤m≤4,
∴3<m≤4.
25.【解答】解:(1)对于直线l:y=﹣x+4,
当x=0时,y=4,
当y=0时,﹣x+4=0,
解得x=4,
∴A(4,0),B(0,4),
对于直线 l2:y=kx+2k(k≠0),
当y=0时,kx+2k=0,
解得:x=﹣2,
∴C(﹣2,0),
故A(4,0),B(0,4),C(﹣2,0);
(2)∵,
∴S1>S2
①当点D在线段BA上时,
AC=4﹣(﹣2)=6,OB=4,
∴12,
∴S2AC×yD=3yD,
∴S1=S△ABC﹣S2=12﹣3yD,
∵,
∴,
解得yD=1,
经检验:yD=1是方程的解,
∴﹣x+4=1,
解得x=3,
∴D(3,1),
∴3k+2k=1,
解得,
∴直线l2的函数表达式为:;
②当点D在线段BA的延长线上时,
3yD,
∴S1=S△ABC+S2=12﹣3yD,
∵,
∴3,
解得yD=﹣2,
经检验yD=﹣2是方程的解,
∴﹣x+4=﹣2,
解得x=6,
∴D(6,﹣2),
∴6k+2k=﹣2,
解得,
∴直线l2的函数表达式为:;
综上所述:直线l2的函数表达式为:或;
(3)如图,作DH⊥x轴交于H,
由(1)得,
∵四边形BCDE是平行四边形,
∴CF=EF,
∵N是BE的中点,M是DE的中点,
∴,,
∴FM+FN,
∴CD取最小值时,FM+FN取得最小值,当CD⊥AB时,CD取最小值,
∵OA=OB=4,
∴∠OAB=45°,
∴,
∴∠ACD=∠CAD=45°,
∴CD=AD,
∴,
∴AH=DH=3,
∴,,
∴BD,
∴6;
∴S BCDE=2S△BDC=6;
故 BCDE的面积为6.
21世纪教育网(www.21cnjy.com)
同课章节目录
