人教版2024—2025学年八年级下册数学期末考试仿真模拟试卷(含答案)
文档属性
| 名称 | 人教版2024—2025学年八年级下册数学期末考试仿真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 742.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 20:53:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年八年级下册数学期末考试仿真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.某校运动队为准备省运动会,对甲,乙两名同学100米短跑进行了6次测试,他们的成绩通过计算得:甲和乙的平均数相等,方差分别是,,则关于甲,乙两人在这次测试中成绩稳定性的描述正确的是( )
A.甲比乙稳定 B.乙比甲稳定
C.甲和乙一样稳定 D.无法比较
2.下列条件中,不能判断△ABC是直角三角形的是( )
A.a:b:c=3:4:5 B.∠A:∠B:∠C=3:4:5
C.∠A+∠B=∠C D.a:b:c=1:2:
3.下列各式中,一定是二次根式的是( )
A. B. C. D.
4.如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE的长为( )
A.4 B.6 C.8 D.10
5.如图, ABCD中,AE平分∠DAB,∠B=100°,则∠DAE=( )
A.100° B.80° C.60° D.40°
6.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.OA=OC,OB=OD
C.AD=BC,AB∥CD D.AB=CD,AD=BC
7.如图,则化简的结果为( )
A.﹣1 B.1 C.2a﹣1 D.1﹣2a
8.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量三个角是否为直角
9.已知,则代数式的值为( )
A. B. C. D.
10.当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,则实数m的值为( )
A.﹣3或0 B.0或1 C.﹣5或﹣3 D.﹣5或1
二、填空题(6小题,每题3分,共18分)
11.某校九(1)班全体学生上周末进行体育测试的成绩统计如下表:
成绩/分 45 50 55 60 65 68 70
人数/人 2 6 10 7 6 5 4
根据表中的信息判断,该班学生这次测试成绩的中位数是 分.
12.在平面直角坐标系中,直线沿x轴向左平移2个单位后,则所得直线的解析式为 .
13.已知点(m,n)在直线y=x+b(b为常数)上,若mn的最小值为﹣1,则b= .
14.如图,在△ABC中,已知点D,E,F分别是AB,AC,BC的中点,△ADE的面积为2,则四边形DBFE的面积为 .
15.如图,是一个长方体硬纸盒,现在A处有一只蚂蚁,想沿着长方体的外表面到达B处吃食物,则蚂蚁爬行的最短距离是 .
16.如图,在△ABC中,AB=5,AC=2,3∠B+∠C=180°,则S△ABC的值为 .
第II卷
人教版2024—2025学年八年级下册数学期末考试仿真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
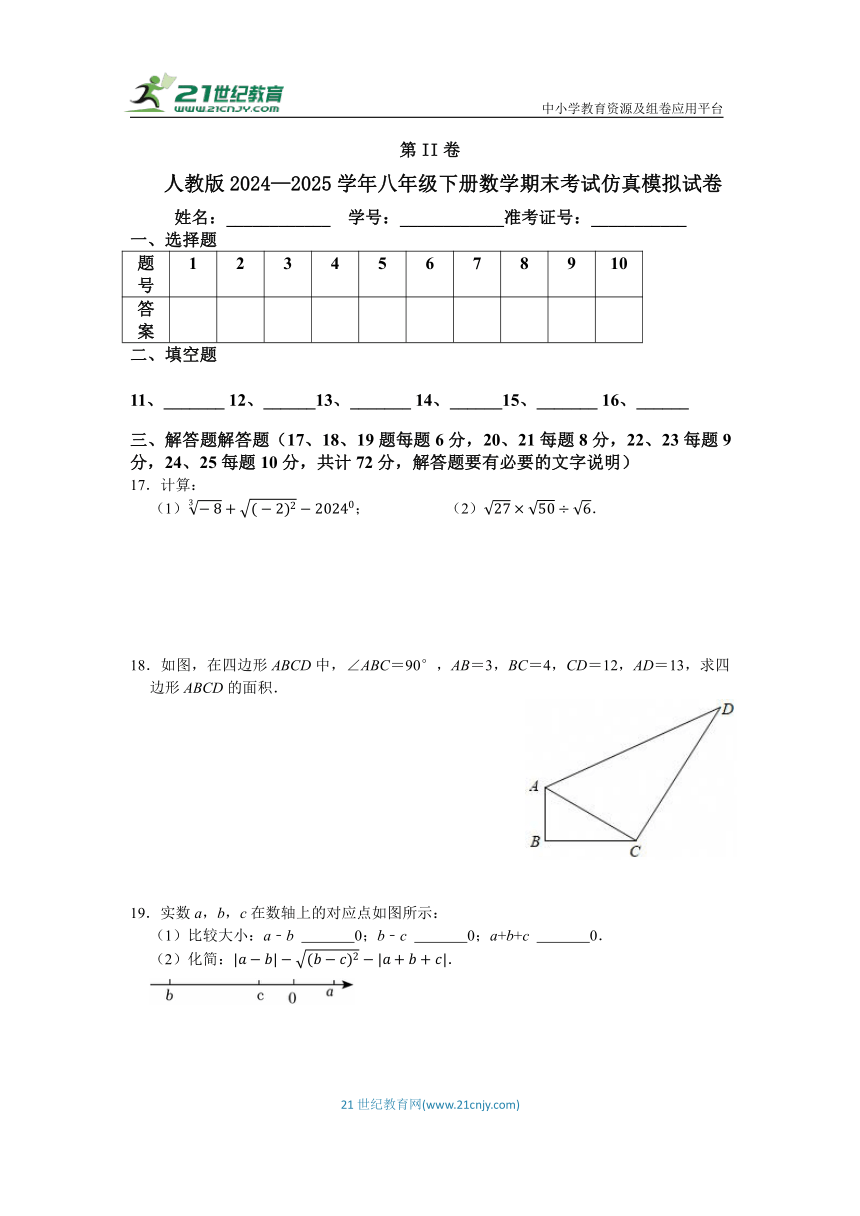
18.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
19.实数a,b,c在数轴上的对应点如图所示:
(1)比较大小:a﹣b 0;b﹣c 0;a+b+c 0.
(2)化简:.
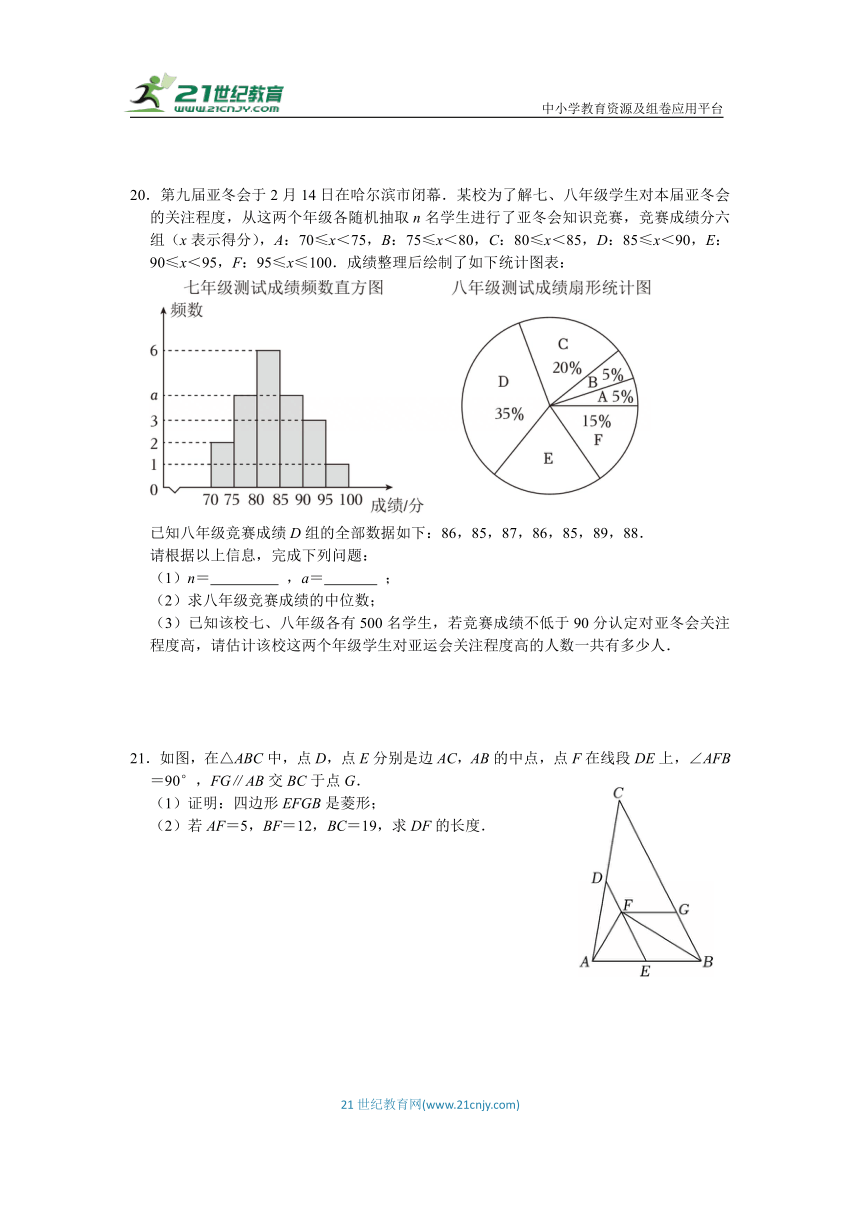
20.第九届亚冬会于2月14日在哈尔滨市闭幕.某校为了解七、八年级学生对本届亚冬会的关注程度,从这两个年级各随机抽取n名学生进行了亚冬会知识竞赛,竞赛成绩分六组(x表示得分),A:70≤x<75,B:75≤x<80,C:80≤x<85,D:85≤x<90,E:90≤x<95,F:95≤x≤100.成绩整理后绘制了如下统计图表:
已知八年级竞赛成绩D组的全部数据如下:86,85,87,86,85,89,88.
请根据以上信息,完成下列问题:
(1)n= ,a= ;
(2)求八年级竞赛成绩的中位数;
(3)已知该校七、八年级各有500名学生,若竞赛成绩不低于90分认定对亚冬会关注程度高,请估计该校这两个年级学生对亚运会关注程度高的人数一共有多少人.
21.如图,在△ABC中,点D,点E分别是边AC,AB的中点,点F在线段DE上,∠AFB=90°,FG∥AB交BC于点G.
(1)证明:四边形EFGB是菱形;
(2)若AF=5,BF=12,BC=19,求DF的长度.
22.如图,直线l分别交x轴和y轴于点A,B,A(3,0),.
(1)求点B的坐标;
(2)若点C在x轴的负半轴上,△ABC的面积为4,求直线BC的解析式.
23.《哪吒2魔童闹海》票房大卖,周边玩偶热销.小洋在网上开设相关周边专卖店,一次,小洋发现一张进货单上的一个信息是:款哪吒玩偶的进货单价比款哪吒玩偶少5元,花500元购进款哪吒玩偶的数量与花750元购进款哪吒玩偶的数量相同.
(1)问:、两款的进货单价分别是多少元?
(2)小洋决定将款玩偶的销售单价定为13元,将款玩偶的销售单价定为20元,小洋打算购进、两款玩偶共100个,且款的数量不小于款的,请你根据计算说明,当、两款各购进多少时,小洋获得的总利润最高,最高为多少?
24.如图1,在中,,,,.动点P从点A出发,沿边以每秒2个单位长的速度运动到点B,动点Q同时从点B出发,沿边以每秒1个单位长的速度运动到点C,设点P,Q运动时间为t(s).
(1)求的度数;
(2)当是等边三角形时,求t的值;
(3)在点P,Q的运动过程中,求当是直角三角形时t的值;
(4)如图2,若D是边的中点,连接,,请直接写出的最小值.
25.定义:对于平面直角坐标系中的点和直线,我们称点是直线的“友谊点”,直线是点的“友谊直线”.特别地,当时,直线(为常数)的“友谊点”为.
(1)已知点,则点的“友谊直线”的解析式为______________;直线的“友谊点”的坐标为_________________;
(2)两点关于轴对称,且点的“友谊直线”经过点和点,求该直线的解析式;
(3)直线不经过第二象限,为直线的“友谊点”.
①若为整数,求点的坐标;
②直线与轴,轴分别相交于两点,,为平面内一点,当以为顶点的四边形为平行四边形时,请直接写出点的坐标.
参考答案
一、选择题
1—10:ABDAD CDDCA
二、填空题
11.【解答】解:根据表格可知,九(1)班全体学生人数为:2+6+10+7+6+5+4=40(人),
第 20 和 21 名同学的成绩的平均值为中位数,(60+60)÷2=60.
故答案为:60.
12.【解答】解:将直线yx﹣3向左平移2个单位后,
得到直线y(x+2)﹣3,
yx,
即yx,
故答案为:yx.
13.【解答】解:将点(m,n)代入y=x+b得,
n=m+b,
则mn=m(m+b)=m2+mb.
因为mn的最小值为﹣1,
所以m>0,且当m时,mn取得最小值,
则,
解得b=±2.
故答案为:±2.
14.【解答】解:∵点D,E,F分别是AB,AC,BC的中点,
∴DE,EF是△ABC的中位线,
∴DE∥BC,EF∥AB,DE=BF=CFBC,EF=AD=BDAB,
∴∠ADE=∠B,∠AED=∠C,∠CEF=∠A,∠CFE=∠B,
∴△ADE≌△DBF≌△EFC(ASA),
∴S△ADE=S△DBF=S△EFC=2,DF=CE,
∴△DEF≌△BFD(SSS),
∴S△DEF=S△DBF=2,
∴四边形DBFE的面积为S△ABC﹣S△ADE﹣S△CEF=8﹣2﹣2=4,
故答案为:4.
15.【解答】解:第一种情况:把我们所看到的左面和上面组成一个平面,
则这个长方形的长和宽分别是18和6,
则所走的最短线段是AB6(cm).
第二种情况:把我们看到的前面与上面组成一个长方形,
则这个长方形的长和宽分别是14和10,
所以走的最短线段是AB2(cm).
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是16和8,
所以走的最短线段是AB8(cm).
∴它需要爬行的最短路径是2cm.
故答案为:2cm.
16.【解答】解:延长BA到D,使AD=AC,连接CD,作CH⊥AB于点H,
∵3∠B+∠C=180°,∠BAC+∠B+∠C=180°,
∴∠BAC=2∠B,
∵AD=AC,
∴∠D=∠ACD,
∴∠BAC=∠D+∠ACD=2∠D,
∴∠B=∠D,
∴CB=CD,
∵CH⊥AB,
∴BH=DH,
∵AB=5,AC=CD=2,
∴BD=7,
∴,
∴,
在Rt△ACH中,,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)
=﹣2+2﹣1
=﹣1;
(2)
=15.
18.【解答】解:∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACDAB BCAC CD3×45×12=36.
故四边形ABCD的面积是36.
19.【解答】解:(1)根据点在数轴上的位置,知:a>0,b<0,c<0;且|b|>|a|>|c|,
∴a﹣b>0,b﹣c<0,a+b+c<0,
故答案为:>,<,<;
(2)原式=a﹣b﹣(c﹣b)+a+b+c=a﹣b﹣c+b+a+b+c=2a+b.
20.【解答】解:(1)八年级测试成绩D组:85≤x<90的频数为7,由扇形统计图知D组占35%,
∴进行测试d 学生数为:n=7÷35%=20(人),
∴2a=20﹣1﹣2﹣3﹣6,
2a=8,
解得:a=4.
故答案为:20;4;
(2)A、B、C三组的频率之和为:5%+5%+20%=30%<50%,
A、B、C、D四组的频率之和为:30%+35%=65%>50%,
∴中位数在D组,将D组数据从小到大排序为85,85,86,86,87,88,89,
∵20×30%=6,第10与第11两个数据为86,87,
∴中位数为;
(3)八年级E:90≤x<95,F:95≤x≤100三组占1﹣30%﹣35%=35%,
共有20×35%=7人,
七年级E:90≤x<95,F:95≤x≤100两组人数为3+1=4人,
两年级共有7+4=11人,
两个年级对亚冬会关注程度稿的人数占样本的,
∴(人),
估计对亚运会关注程度高的人数一共有275人.
21.【解答】(1)证明:∵点D,点E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴EF∥BG,
∵FG∥AB,
∴四边形BEFG是平行四边形,
∵∠AFB=90°,
∴FE=BEAB,
∴四边形EFGB是菱形;
(2)解:∵点D,点E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴DEBC19,
在△ABF中,
∵∠AFB=90°,
∴EFAB13,
∴DF=DE﹣EF3.
22.【解答】解:(1)∵A(3,0),.
∴BO2,
∴B的坐标为(0,2);
(2)∵△ABC的面积为4,
∴4,
∴BC×2=4,即BC=4,
∵AO=3,
∴CO=4﹣3=1,
∴C(﹣1,0),
设直线BC的解析式为y=kx+b,则,
解得,
∴直线BC的解析式为y=2x+2.
23.【解答】解:(1)解:设款的进货单价是元,则款的进货单价是元,
根据题意,可得,解得
经检验,是该方程的解,
,
答:款的进货单价是10元,则款的进货单价是15元.
(2)解:设购进款个,则购进款个,
∵款的数量不小于款的,
,
解得:,
设总利润为,则
,
随的增大而减少,
当取得最小整数解25时,取得最大值,最大值为
此时,则
答:购进款个,购进款个时,获得的总利润最高,最高为450元.
24.【解答】解:(1)∵,,
∴,
∴是直角三角形,
∴;
(2)依题意得:, ,
∴,
∵,
∴当时,是等边三角形,
∴,
解得:,
∴当是等边三角形时,t的值为;
(3)当是直角三角形时,有以下两种情况:
①当时,如图1所示:
∵,
∴,
在中,,
∴,
解得:;
②当时,如图2所示:
∵,
∴,
∴,
∴,
解得:,
综上所述:当是直角三角形时,t的值为5或8;
(4)过点C作于点F,在的延长线上取一点E,使,连接,,,如图3所示:
∴是线段的垂直平分线,
∴,,
∴是等腰三角形,,
∴,
由(1)可知:,
又∵,
∴,
∴,
∴等腰三角形是等边三角形,
∴,
∵点D是的中点,
∴,,
在中,由勾股定理得:,
根据“两点之间线段最短”得:,
∴,
∴的最小值为15,
∵,
∴的最小值为15.
25.【解答】解:(1)解:由题意得,点的“友谊直线”的解析式为,
∵,
∴直线的解析式为,
∴直线的“友谊点”的坐标为.
(2)解:将代入,得,解得,
∴直线解析式为,
根据定义,的“友谊点”的坐标为,
∵两点关于轴对称,
∴点的坐标为,
将代入,得,
解得,
∴直线的解析式为.
(3)解:①∵直线不经过第二象限,
∴,
解得,
又∵为整数,
∴的值为2,
根据题意,直线的“友谊点”的坐标为,
∴点的坐标为.
②当时,,
∴点的坐标为,
当时,即,
解得,
∴点的坐标为,
∵直线不经过第二象限,
∴,
∴,
∵,
∴,
解得,
∴,
∴,
当为对角线时,则,
∴,
∴点N的坐标为;
当为对角线时,则,
∴,
∴点N的坐标为;
当为对角线时,则,
∴,
∴点N的坐标为;
综上所述,点的坐标为或或.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年八年级下册数学期末考试仿真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.某校运动队为准备省运动会,对甲,乙两名同学100米短跑进行了6次测试,他们的成绩通过计算得:甲和乙的平均数相等,方差分别是,,则关于甲,乙两人在这次测试中成绩稳定性的描述正确的是( )
A.甲比乙稳定 B.乙比甲稳定
C.甲和乙一样稳定 D.无法比较
2.下列条件中,不能判断△ABC是直角三角形的是( )
A.a:b:c=3:4:5 B.∠A:∠B:∠C=3:4:5
C.∠A+∠B=∠C D.a:b:c=1:2:
3.下列各式中,一定是二次根式的是( )
A. B. C. D.
4.如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE的长为( )
A.4 B.6 C.8 D.10
5.如图, ABCD中,AE平分∠DAB,∠B=100°,则∠DAE=( )
A.100° B.80° C.60° D.40°
6.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.OA=OC,OB=OD
C.AD=BC,AB∥CD D.AB=CD,AD=BC
7.如图,则化简的结果为( )
A.﹣1 B.1 C.2a﹣1 D.1﹣2a
8.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量三个角是否为直角
9.已知,则代数式的值为( )
A. B. C. D.
10.当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,则实数m的值为( )
A.﹣3或0 B.0或1 C.﹣5或﹣3 D.﹣5或1
二、填空题(6小题,每题3分,共18分)
11.某校九(1)班全体学生上周末进行体育测试的成绩统计如下表:
成绩/分 45 50 55 60 65 68 70
人数/人 2 6 10 7 6 5 4
根据表中的信息判断,该班学生这次测试成绩的中位数是 分.
12.在平面直角坐标系中,直线沿x轴向左平移2个单位后,则所得直线的解析式为 .
13.已知点(m,n)在直线y=x+b(b为常数)上,若mn的最小值为﹣1,则b= .
14.如图,在△ABC中,已知点D,E,F分别是AB,AC,BC的中点,△ADE的面积为2,则四边形DBFE的面积为 .
15.如图,是一个长方体硬纸盒,现在A处有一只蚂蚁,想沿着长方体的外表面到达B处吃食物,则蚂蚁爬行的最短距离是 .
16.如图,在△ABC中,AB=5,AC=2,3∠B+∠C=180°,则S△ABC的值为 .
第II卷
人教版2024—2025学年八年级下册数学期末考试仿真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
19.实数a,b,c在数轴上的对应点如图所示:
(1)比较大小:a﹣b 0;b﹣c 0;a+b+c 0.
(2)化简:.
20.第九届亚冬会于2月14日在哈尔滨市闭幕.某校为了解七、八年级学生对本届亚冬会的关注程度,从这两个年级各随机抽取n名学生进行了亚冬会知识竞赛,竞赛成绩分六组(x表示得分),A:70≤x<75,B:75≤x<80,C:80≤x<85,D:85≤x<90,E:90≤x<95,F:95≤x≤100.成绩整理后绘制了如下统计图表:
已知八年级竞赛成绩D组的全部数据如下:86,85,87,86,85,89,88.
请根据以上信息,完成下列问题:
(1)n= ,a= ;
(2)求八年级竞赛成绩的中位数;
(3)已知该校七、八年级各有500名学生,若竞赛成绩不低于90分认定对亚冬会关注程度高,请估计该校这两个年级学生对亚运会关注程度高的人数一共有多少人.
21.如图,在△ABC中,点D,点E分别是边AC,AB的中点,点F在线段DE上,∠AFB=90°,FG∥AB交BC于点G.
(1)证明:四边形EFGB是菱形;
(2)若AF=5,BF=12,BC=19,求DF的长度.
22.如图,直线l分别交x轴和y轴于点A,B,A(3,0),.
(1)求点B的坐标;
(2)若点C在x轴的负半轴上,△ABC的面积为4,求直线BC的解析式.
23.《哪吒2魔童闹海》票房大卖,周边玩偶热销.小洋在网上开设相关周边专卖店,一次,小洋发现一张进货单上的一个信息是:款哪吒玩偶的进货单价比款哪吒玩偶少5元,花500元购进款哪吒玩偶的数量与花750元购进款哪吒玩偶的数量相同.
(1)问:、两款的进货单价分别是多少元?
(2)小洋决定将款玩偶的销售单价定为13元,将款玩偶的销售单价定为20元,小洋打算购进、两款玩偶共100个,且款的数量不小于款的,请你根据计算说明,当、两款各购进多少时,小洋获得的总利润最高,最高为多少?
24.如图1,在中,,,,.动点P从点A出发,沿边以每秒2个单位长的速度运动到点B,动点Q同时从点B出发,沿边以每秒1个单位长的速度运动到点C,设点P,Q运动时间为t(s).
(1)求的度数;
(2)当是等边三角形时,求t的值;
(3)在点P,Q的运动过程中,求当是直角三角形时t的值;
(4)如图2,若D是边的中点,连接,,请直接写出的最小值.
25.定义:对于平面直角坐标系中的点和直线,我们称点是直线的“友谊点”,直线是点的“友谊直线”.特别地,当时,直线(为常数)的“友谊点”为.
(1)已知点,则点的“友谊直线”的解析式为______________;直线的“友谊点”的坐标为_________________;
(2)两点关于轴对称,且点的“友谊直线”经过点和点,求该直线的解析式;
(3)直线不经过第二象限,为直线的“友谊点”.
①若为整数,求点的坐标;
②直线与轴,轴分别相交于两点,,为平面内一点,当以为顶点的四边形为平行四边形时,请直接写出点的坐标.
参考答案
一、选择题
1—10:ABDAD CDDCA
二、填空题
11.【解答】解:根据表格可知,九(1)班全体学生人数为:2+6+10+7+6+5+4=40(人),
第 20 和 21 名同学的成绩的平均值为中位数,(60+60)÷2=60.
故答案为:60.
12.【解答】解:将直线yx﹣3向左平移2个单位后,
得到直线y(x+2)﹣3,
yx,
即yx,
故答案为:yx.
13.【解答】解:将点(m,n)代入y=x+b得,
n=m+b,
则mn=m(m+b)=m2+mb.
因为mn的最小值为﹣1,
所以m>0,且当m时,mn取得最小值,
则,
解得b=±2.
故答案为:±2.
14.【解答】解:∵点D,E,F分别是AB,AC,BC的中点,
∴DE,EF是△ABC的中位线,
∴DE∥BC,EF∥AB,DE=BF=CFBC,EF=AD=BDAB,
∴∠ADE=∠B,∠AED=∠C,∠CEF=∠A,∠CFE=∠B,
∴△ADE≌△DBF≌△EFC(ASA),
∴S△ADE=S△DBF=S△EFC=2,DF=CE,
∴△DEF≌△BFD(SSS),
∴S△DEF=S△DBF=2,
∴四边形DBFE的面积为S△ABC﹣S△ADE﹣S△CEF=8﹣2﹣2=4,
故答案为:4.
15.【解答】解:第一种情况:把我们所看到的左面和上面组成一个平面,
则这个长方形的长和宽分别是18和6,
则所走的最短线段是AB6(cm).
第二种情况:把我们看到的前面与上面组成一个长方形,
则这个长方形的长和宽分别是14和10,
所以走的最短线段是AB2(cm).
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是16和8,
所以走的最短线段是AB8(cm).
∴它需要爬行的最短路径是2cm.
故答案为:2cm.
16.【解答】解:延长BA到D,使AD=AC,连接CD,作CH⊥AB于点H,
∵3∠B+∠C=180°,∠BAC+∠B+∠C=180°,
∴∠BAC=2∠B,
∵AD=AC,
∴∠D=∠ACD,
∴∠BAC=∠D+∠ACD=2∠D,
∴∠B=∠D,
∴CB=CD,
∵CH⊥AB,
∴BH=DH,
∵AB=5,AC=CD=2,
∴BD=7,
∴,
∴,
在Rt△ACH中,,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)
=﹣2+2﹣1
=﹣1;
(2)
=15.
18.【解答】解:∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACDAB BCAC CD3×45×12=36.
故四边形ABCD的面积是36.
19.【解答】解:(1)根据点在数轴上的位置,知:a>0,b<0,c<0;且|b|>|a|>|c|,
∴a﹣b>0,b﹣c<0,a+b+c<0,
故答案为:>,<,<;
(2)原式=a﹣b﹣(c﹣b)+a+b+c=a﹣b﹣c+b+a+b+c=2a+b.
20.【解答】解:(1)八年级测试成绩D组:85≤x<90的频数为7,由扇形统计图知D组占35%,
∴进行测试d 学生数为:n=7÷35%=20(人),
∴2a=20﹣1﹣2﹣3﹣6,
2a=8,
解得:a=4.
故答案为:20;4;
(2)A、B、C三组的频率之和为:5%+5%+20%=30%<50%,
A、B、C、D四组的频率之和为:30%+35%=65%>50%,
∴中位数在D组,将D组数据从小到大排序为85,85,86,86,87,88,89,
∵20×30%=6,第10与第11两个数据为86,87,
∴中位数为;
(3)八年级E:90≤x<95,F:95≤x≤100三组占1﹣30%﹣35%=35%,
共有20×35%=7人,
七年级E:90≤x<95,F:95≤x≤100两组人数为3+1=4人,
两年级共有7+4=11人,
两个年级对亚冬会关注程度稿的人数占样本的,
∴(人),
估计对亚运会关注程度高的人数一共有275人.
21.【解答】(1)证明:∵点D,点E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴EF∥BG,
∵FG∥AB,
∴四边形BEFG是平行四边形,
∵∠AFB=90°,
∴FE=BEAB,
∴四边形EFGB是菱形;
(2)解:∵点D,点E分别是边AC,AB的中点,
∴DE是△ABC的中位线,
∴DEBC19,
在△ABF中,
∵∠AFB=90°,
∴EFAB13,
∴DF=DE﹣EF3.
22.【解答】解:(1)∵A(3,0),.
∴BO2,
∴B的坐标为(0,2);
(2)∵△ABC的面积为4,
∴4,
∴BC×2=4,即BC=4,
∵AO=3,
∴CO=4﹣3=1,
∴C(﹣1,0),
设直线BC的解析式为y=kx+b,则,
解得,
∴直线BC的解析式为y=2x+2.
23.【解答】解:(1)解:设款的进货单价是元,则款的进货单价是元,
根据题意,可得,解得
经检验,是该方程的解,
,
答:款的进货单价是10元,则款的进货单价是15元.
(2)解:设购进款个,则购进款个,
∵款的数量不小于款的,
,
解得:,
设总利润为,则
,
随的增大而减少,
当取得最小整数解25时,取得最大值,最大值为
此时,则
答:购进款个,购进款个时,获得的总利润最高,最高为450元.
24.【解答】解:(1)∵,,
∴,
∴是直角三角形,
∴;
(2)依题意得:, ,
∴,
∵,
∴当时,是等边三角形,
∴,
解得:,
∴当是等边三角形时,t的值为;
(3)当是直角三角形时,有以下两种情况:
①当时,如图1所示:
∵,
∴,
在中,,
∴,
解得:;
②当时,如图2所示:
∵,
∴,
∴,
∴,
解得:,
综上所述:当是直角三角形时,t的值为5或8;
(4)过点C作于点F,在的延长线上取一点E,使,连接,,,如图3所示:
∴是线段的垂直平分线,
∴,,
∴是等腰三角形,,
∴,
由(1)可知:,
又∵,
∴,
∴,
∴等腰三角形是等边三角形,
∴,
∵点D是的中点,
∴,,
在中,由勾股定理得:,
根据“两点之间线段最短”得:,
∴,
∴的最小值为15,
∵,
∴的最小值为15.
25.【解答】解:(1)解:由题意得,点的“友谊直线”的解析式为,
∵,
∴直线的解析式为,
∴直线的“友谊点”的坐标为.
(2)解:将代入,得,解得,
∴直线解析式为,
根据定义,的“友谊点”的坐标为,
∵两点关于轴对称,
∴点的坐标为,
将代入,得,
解得,
∴直线的解析式为.
(3)解:①∵直线不经过第二象限,
∴,
解得,
又∵为整数,
∴的值为2,
根据题意,直线的“友谊点”的坐标为,
∴点的坐标为.
②当时,,
∴点的坐标为,
当时,即,
解得,
∴点的坐标为,
∵直线不经过第二象限,
∴,
∴,
∵,
∴,
解得,
∴,
∴,
当为对角线时,则,
∴,
∴点N的坐标为;
当为对角线时,则,
∴,
∴点N的坐标为;
当为对角线时,则,
∴,
∴点N的坐标为;
综上所述,点的坐标为或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
