苏科版2024—2025学年八年级下册数学期末考试仿真模拟试卷(含答案)
文档属性
| 名称 | 苏科版2024—2025学年八年级下册数学期末考试仿真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 665.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 21:06:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏科版2024—2025学年八年级下册数学期末考试仿真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列式子中,不属于二次根式的是( )
A. B. C. D.
2.剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,摸到黑球是( )
A.必然事件 B.随机事件
C.不可能事件 D.以上事件都有可能
4.已知长方形的两条边长为x、y,面积是4,那么y关于x的函数的图象是( )
A. B. C. D.
5.调查某班30名同学的跳高成绩时,在收集到的数据中,不足1.50米的数出现的频率是0.82,则达到或超过1.50米的数出现的频率是( )
A.0.82 B.0.18 C.30 D.1
6.如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
7.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当∠ABC=90°,平行四边形ABCD是矩形
B.当AC=BD,平行四边形ABCD是矩形
C.当AB=BC,平行四边形ABCD是菱形
D.当AC⊥BD,平行四边形ABCD是正方形
8.如图,菱形ABCD的对角线AC、BD交于点O,菱形ABCD的周长为40,直线EF过点O,且与AD,BC分别交于点E、F,若OE=5,则四边形ABFE的周长是( )
A.30 B.25 C.20 D.15
9.如图,将△ABC绕点A逆时针旋转70°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小是( )
A.45° B.55° C.60° D.100°
10.若分式方程无解,则m的值是( )
A.0 B.﹣1 C.﹣2 D.﹣1或﹣2
二、填空题(6小题,每题3分,共18分)
11.分别写有数字、、﹣1、0、π的五张大小和质地均相同的卡片,从中任意抽取一张,抽到无理数的概率是 .
12.从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中有 个白球.
13.计算: .
14.如图,点P是等边三角形ABC内的一点,,PB=3,,则S△ABP+S△BPC= .
15.如图,四边形ABCD 为平行四边形,且DB平分∠ABC,作DE⊥BC,垂足为E.若BD=24,AC=10,则DE= .
16.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=5,则GH的最小值是 .
第II卷
苏科版2024—2025学年八年级下册数学期末考试仿真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再取一个合适的整数x,使得分式的值为整数,并求此时分式的值.
18.计算:
(1);
(2).
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
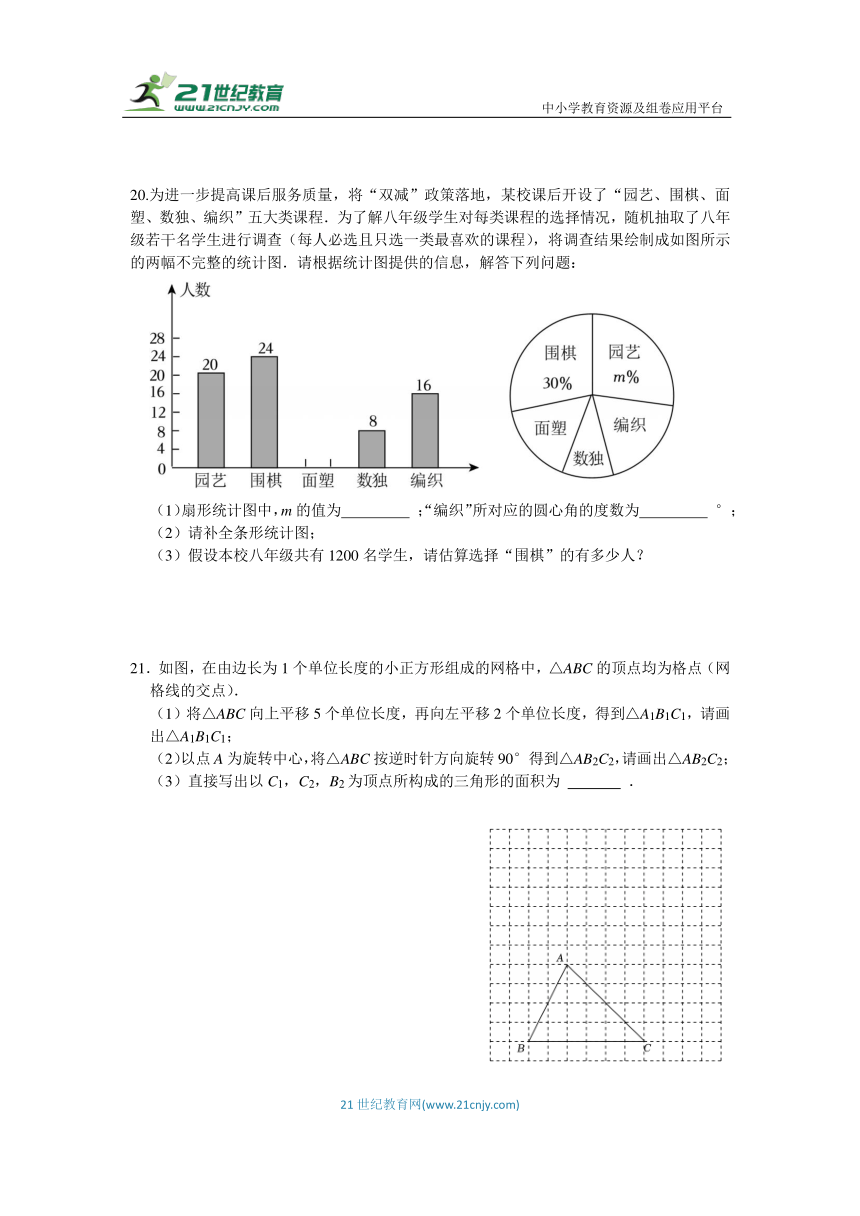
20.为进一步提高课后服务质量,将“双减”政策落地,某校课后开设了“园艺、围棋、面塑、数独、编织”五大类课程.为了解八年级学生对每类课程的选择情况,随机抽取了八年级若干名学生进行调查(每人必选且只选一类最喜欢的课程),将调查结果绘制成如图所示的两幅不完整的统计图.请根据统计图提供的信息,解答下列问题:
(1)扇形统计图中,m的值为 ;“编织”所对应的圆心角的度数为 °;
(2)请补全条形统计图;
(3)假设本校八年级共有1200名学生,请估算选择“围棋”的有多少人?
21.如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向上平移5个单位长度,再向左平移2个单位长度,得到△A1B1C1,请画出△A1B1C1;
(2)以点A为旋转中心,将△ABC按逆时针方向旋转90°得到△AB2C2,请画出△AB2C2;
(3)直接写出以C1,C2,B2为顶点所构成的三角形的面积为 .
22.如图,在 ABCD中,点E,F分别在BA,DC的延长线上,且BE=DF.连结AF,交BC于点H,连结EC.
(1)求证:四边形EAFC是平行四边形.
(2)若∠E=∠D=70°,求∠AHB的度数.
23.“开心水果店”用3200元购进一批糖心苹果,很快售完.该店又用3000元购进第二批这种糖心苹果,已知第二批的进货价比第一批的进货价每千克少了1元,第一批购进数量比第二批少20%.
(1)求第一批购进的苹果每千克多少元.
(2)该水果店销售第一批苹果时,每千克的售价为6元,全部售完后购进第二批苹果,发现第二批苹果品质不如第一批,该店主决定降价销售,在销售过程中仍有5%的苹果出现了腐坏现象、不能销售、若该水果店售完这两批苹果后,总获利不低于2875元,则第二批销售最多能降价多少元?
24.如图,在平面直角坐标系内,一次函数与反比例函数交于C(2,m)、D(6,n)两点.
(1)求反比例函数的解析式;
(2)若一次函数与x轴、y轴分别交于A、B两点,过△AOB的顶点能不能画出直线把△AOB分成面积相等的两部分?若能,请求出这样的直线所对应的函数表达式.
25.新定义:如果两个实数a,b使得关于x的分式方程的解是成立,那么我们就把实数a,b组成的数对[a,b]称为关于x的分式方程的一个“关联数对”.
例如:a=2,b=﹣5使得关于x的分式方程的解是成立,所以数对[2,﹣5]就是关于x的分式方程的一个“关联数对”.
(1)判断下列数对是否为关于x的分式方程的“关联数对”,若是,请在括号内打“√”.若不是,打“×”.
①[﹣1,﹣1] ;②[3,4] ;
③[2,﹣5] ; ④[1,1] ;
(2)若数对[n2﹣3,﹣n2]是关于x的分式方程的“关联数对”,求n的值;
(3)若数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,且关于x的方程有整数解,求整数m的值.
参考答案
选择题
1—10:CABCB BDABD
二、填空题
11.【解答】解:∵写有数字、、﹣1、0、π的五张大小和质地均相同的卡片,、π是无理数,
∴从中任意抽取一张,抽到无理数的概率是:.
故答案为:.
12.【解答】解:摸了150次,其中有50次摸到黑球,则摸到黑球的频率是,
设口袋中大约有x个白球,则,
解得x=20.
故答案为:20.
13.【解答】解:原式
=1,
故答案为:1.
14.【解答】解:将△APC绕点A旋转60°得到△AEB,过点B作BF⊥AP于点F,
∴AE=AP,BE=PC=3,∠PAE=60°,
∴△AEP是等边三角形,
∴EP=AP,∠APE=60°,
∵BE2=12,PB2+PE2=9+3=12,
∴BE2=PE2+PB2,
∴∠BPE=90°,
∴∠APB=150°,
∴∠BPF=30°,
∴BFPB,
∵BE=2PE,∠BPE=90°,
∴∠EBP=30°,
∴∠BEP=90°﹣30°=60°,
∵∠AEP=60°,
∴∠APC=∠AEB=120°,
∴∠BPC=360°﹣150°﹣120°=90°,
∴S△APB+S△PBC3×2.
故答案为:.
15.【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵DB平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴OBBD=4,OCAC=5,AC⊥BD,
∴∠BOC=90°,
∴BC13,
∵DE⊥BC,
∴菱形ABCD的面积=BC DEAC BD,
即13DE10×24,
解得:DE,
故答案为:.
16.【解答】解:连接AC、AP、CP,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,∠BAD=∠B=∠C=90°,
∴AC10,
∵P是线段EF的中点,
∴APEF=2.5,
∵PG⊥BC,PH⊥CD,
∴∠PGC=∠PHC=90°,
∴四边形PGCH是矩形,
∴GH=CP,
当A、P、C三点共线时,CP最小=AC﹣AP=10﹣2.5=7.5,
∴GH的最小值是7.5,
故答案为:7.5.
三、解答题
17.【解答】解:
,
∵当x=±2时,原分式无意义,
∴x可以为1,
当x=1时,原式2(答案不唯一).
18.【解答】解:(1)原式=(53)
=2
;
(2)原式=1﹣2
=1.
19.【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
20.【解答】解:(1)用选择围棋的人数除以其人数占比可得:24÷30%=80(人),
∴本次共调查了80人,
∴,
∴m=25;
“编织”所对应的圆心角的度数为;
故答案为:25,72;
(2)选择面塑的人数为80﹣20﹣24﹣8﹣16=12(人),
补全统计图如下:
(3)1200×30%=360(人),
答:估计选择“围棋”的有360人.
21.【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△AB2C2;即为所求;
(3)以C1,C2,B2为顶点所构成的三角形的面积6×2=6.
故答案为:6.
22.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AE∥CF,
∵BE=DF,
∴BE﹣AB=DF﹣CD,
即AE=CF
∴四边形EAFC是平行四边形;
(2)解:∵四边形EAFC是平行四边形,
∴∠B=∠D,AF∥EC,
∴∠BAH=∠E=70°,
∵∠D=∠E=70°,
∴∠BAH=∠B=70°,
∴∠AHB=40°.
23.【解答】解:(1)设第一批购进的苹果每千克x元,则第二批购进的苹果每千克(x﹣1)元,
根据题意得:,
解得:x=4,
经检验,x=4是原方程的解,且符合题意,
答:第一批购进的苹果每千克4元;
(2)由(1)可知,第一批购进苹果数量为3200÷4=800(千克),
第二批购进苹果数量为3000÷(4﹣1)=1000(千克),
设第二批销售能降价a元,
根据题意得:6×800﹣3200+(6﹣a)×1000(1﹣5%)﹣3000≥2875,
解得:a≤1.5,
答:第二批销售最多能降价1.5元.
24.【解答】解:(1)由题意可得:,
∴,代入,
得:,
∴;
(2)对于,
当x=0时,y=﹣2,当y=0时,,解得,x=8,
∴A(8,0),B(0,﹣2),
∵直线把△AOB分成面积相等的两部分,
设△AOB三边OA、OB、AB的中点分别为E,F,G,则有:
E(4,0),F(0,﹣1),即G(4,﹣1),
设直线BE的解析式为y=k1x+b,
把B(0,﹣2),E(4,0)代入y=k1x+b,得:
,
解得,
∴直;
同理可求直线AF的解析式为;直线OG的解析式为;
如图,
25.【解答】解:(1)当a=﹣1,b=﹣1时,分式方程为,,
∵,
∴①[﹣1,﹣1]不是关于x的分式方程的“关联数对”;
当a=3,b=4时,分式方程为,
解得:x=1,
∵,
∴②[3,4]不是关于x的分式方程的“关联数对”;
当a=2,b=﹣5时,分式方程为,
解得,
∵,
∴③[2,﹣5]是关于x的分式方程的“关联数对”;
当a=1,b=1时,分式方程为,
此方程无解,
∴④[1,1]是关于x的分式方程的“关联数对”;
故答案为:①×;②×;③√;④×.
(2)∵数对[n2﹣3,﹣n2]是关于x的分式方程的“关联数对”,
∴,
解得:,
∴,
解得;
(3)∵数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,
∴,,
∴m(m﹣k)+1=k,
解得,
∵可化为k(m+1)x﹣m(m+1)+(m+1)=﹣2mx,
∴(m+1)2x=(m+1)(m﹣1),
解得:,
∵方程有整数解,
∴整数m+1=±1,±2,即m=0,﹣2,1,﹣3,
又m≠0,k≠1,
∴m+1≠m2+1
∴m=﹣2,﹣3.
21世纪教育网(www.21cnjy.com)
苏科版2024—2025学年八年级下册数学期末考试仿真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列式子中,不属于二次根式的是( )
A. B. C. D.
2.剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,摸到黑球是( )
A.必然事件 B.随机事件
C.不可能事件 D.以上事件都有可能
4.已知长方形的两条边长为x、y,面积是4,那么y关于x的函数的图象是( )
A. B. C. D.
5.调查某班30名同学的跳高成绩时,在收集到的数据中,不足1.50米的数出现的频率是0.82,则达到或超过1.50米的数出现的频率是( )
A.0.82 B.0.18 C.30 D.1
6.如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
7.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当∠ABC=90°,平行四边形ABCD是矩形
B.当AC=BD,平行四边形ABCD是矩形
C.当AB=BC,平行四边形ABCD是菱形
D.当AC⊥BD,平行四边形ABCD是正方形
8.如图,菱形ABCD的对角线AC、BD交于点O,菱形ABCD的周长为40,直线EF过点O,且与AD,BC分别交于点E、F,若OE=5,则四边形ABFE的周长是( )
A.30 B.25 C.20 D.15
9.如图,将△ABC绕点A逆时针旋转70°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小是( )
A.45° B.55° C.60° D.100°
10.若分式方程无解,则m的值是( )
A.0 B.﹣1 C.﹣2 D.﹣1或﹣2
二、填空题(6小题,每题3分,共18分)
11.分别写有数字、、﹣1、0、π的五张大小和质地均相同的卡片,从中任意抽取一张,抽到无理数的概率是 .
12.从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中有 个白球.
13.计算: .
14.如图,点P是等边三角形ABC内的一点,,PB=3,,则S△ABP+S△BPC= .
15.如图,四边形ABCD 为平行四边形,且DB平分∠ABC,作DE⊥BC,垂足为E.若BD=24,AC=10,则DE= .
16.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=5,则GH的最小值是 .
第II卷
苏科版2024—2025学年八年级下册数学期末考试仿真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再取一个合适的整数x,使得分式的值为整数,并求此时分式的值.
18.计算:
(1);
(2).
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
20.为进一步提高课后服务质量,将“双减”政策落地,某校课后开设了“园艺、围棋、面塑、数独、编织”五大类课程.为了解八年级学生对每类课程的选择情况,随机抽取了八年级若干名学生进行调查(每人必选且只选一类最喜欢的课程),将调查结果绘制成如图所示的两幅不完整的统计图.请根据统计图提供的信息,解答下列问题:
(1)扇形统计图中,m的值为 ;“编织”所对应的圆心角的度数为 °;
(2)请补全条形统计图;
(3)假设本校八年级共有1200名学生,请估算选择“围棋”的有多少人?
21.如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向上平移5个单位长度,再向左平移2个单位长度,得到△A1B1C1,请画出△A1B1C1;
(2)以点A为旋转中心,将△ABC按逆时针方向旋转90°得到△AB2C2,请画出△AB2C2;
(3)直接写出以C1,C2,B2为顶点所构成的三角形的面积为 .
22.如图,在 ABCD中,点E,F分别在BA,DC的延长线上,且BE=DF.连结AF,交BC于点H,连结EC.
(1)求证:四边形EAFC是平行四边形.
(2)若∠E=∠D=70°,求∠AHB的度数.
23.“开心水果店”用3200元购进一批糖心苹果,很快售完.该店又用3000元购进第二批这种糖心苹果,已知第二批的进货价比第一批的进货价每千克少了1元,第一批购进数量比第二批少20%.
(1)求第一批购进的苹果每千克多少元.
(2)该水果店销售第一批苹果时,每千克的售价为6元,全部售完后购进第二批苹果,发现第二批苹果品质不如第一批,该店主决定降价销售,在销售过程中仍有5%的苹果出现了腐坏现象、不能销售、若该水果店售完这两批苹果后,总获利不低于2875元,则第二批销售最多能降价多少元?
24.如图,在平面直角坐标系内,一次函数与反比例函数交于C(2,m)、D(6,n)两点.
(1)求反比例函数的解析式;
(2)若一次函数与x轴、y轴分别交于A、B两点,过△AOB的顶点能不能画出直线把△AOB分成面积相等的两部分?若能,请求出这样的直线所对应的函数表达式.
25.新定义:如果两个实数a,b使得关于x的分式方程的解是成立,那么我们就把实数a,b组成的数对[a,b]称为关于x的分式方程的一个“关联数对”.
例如:a=2,b=﹣5使得关于x的分式方程的解是成立,所以数对[2,﹣5]就是关于x的分式方程的一个“关联数对”.
(1)判断下列数对是否为关于x的分式方程的“关联数对”,若是,请在括号内打“√”.若不是,打“×”.
①[﹣1,﹣1] ;②[3,4] ;
③[2,﹣5] ; ④[1,1] ;
(2)若数对[n2﹣3,﹣n2]是关于x的分式方程的“关联数对”,求n的值;
(3)若数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,且关于x的方程有整数解,求整数m的值.
参考答案
选择题
1—10:CABCB BDABD
二、填空题
11.【解答】解:∵写有数字、、﹣1、0、π的五张大小和质地均相同的卡片,、π是无理数,
∴从中任意抽取一张,抽到无理数的概率是:.
故答案为:.
12.【解答】解:摸了150次,其中有50次摸到黑球,则摸到黑球的频率是,
设口袋中大约有x个白球,则,
解得x=20.
故答案为:20.
13.【解答】解:原式
=1,
故答案为:1.
14.【解答】解:将△APC绕点A旋转60°得到△AEB,过点B作BF⊥AP于点F,
∴AE=AP,BE=PC=3,∠PAE=60°,
∴△AEP是等边三角形,
∴EP=AP,∠APE=60°,
∵BE2=12,PB2+PE2=9+3=12,
∴BE2=PE2+PB2,
∴∠BPE=90°,
∴∠APB=150°,
∴∠BPF=30°,
∴BFPB,
∵BE=2PE,∠BPE=90°,
∴∠EBP=30°,
∴∠BEP=90°﹣30°=60°,
∵∠AEP=60°,
∴∠APC=∠AEB=120°,
∴∠BPC=360°﹣150°﹣120°=90°,
∴S△APB+S△PBC3×2.
故答案为:.
15.【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵DB平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴OBBD=4,OCAC=5,AC⊥BD,
∴∠BOC=90°,
∴BC13,
∵DE⊥BC,
∴菱形ABCD的面积=BC DEAC BD,
即13DE10×24,
解得:DE,
故答案为:.
16.【解答】解:连接AC、AP、CP,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,∠BAD=∠B=∠C=90°,
∴AC10,
∵P是线段EF的中点,
∴APEF=2.5,
∵PG⊥BC,PH⊥CD,
∴∠PGC=∠PHC=90°,
∴四边形PGCH是矩形,
∴GH=CP,
当A、P、C三点共线时,CP最小=AC﹣AP=10﹣2.5=7.5,
∴GH的最小值是7.5,
故答案为:7.5.
三、解答题
17.【解答】解:
,
∵当x=±2时,原分式无意义,
∴x可以为1,
当x=1时,原式2(答案不唯一).
18.【解答】解:(1)原式=(53)
=2
;
(2)原式=1﹣2
=1.
19.【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
20.【解答】解:(1)用选择围棋的人数除以其人数占比可得:24÷30%=80(人),
∴本次共调查了80人,
∴,
∴m=25;
“编织”所对应的圆心角的度数为;
故答案为:25,72;
(2)选择面塑的人数为80﹣20﹣24﹣8﹣16=12(人),
补全统计图如下:
(3)1200×30%=360(人),
答:估计选择“围棋”的有360人.
21.【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△AB2C2;即为所求;
(3)以C1,C2,B2为顶点所构成的三角形的面积6×2=6.
故答案为:6.
22.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AE∥CF,
∵BE=DF,
∴BE﹣AB=DF﹣CD,
即AE=CF
∴四边形EAFC是平行四边形;
(2)解:∵四边形EAFC是平行四边形,
∴∠B=∠D,AF∥EC,
∴∠BAH=∠E=70°,
∵∠D=∠E=70°,
∴∠BAH=∠B=70°,
∴∠AHB=40°.
23.【解答】解:(1)设第一批购进的苹果每千克x元,则第二批购进的苹果每千克(x﹣1)元,
根据题意得:,
解得:x=4,
经检验,x=4是原方程的解,且符合题意,
答:第一批购进的苹果每千克4元;
(2)由(1)可知,第一批购进苹果数量为3200÷4=800(千克),
第二批购进苹果数量为3000÷(4﹣1)=1000(千克),
设第二批销售能降价a元,
根据题意得:6×800﹣3200+(6﹣a)×1000(1﹣5%)﹣3000≥2875,
解得:a≤1.5,
答:第二批销售最多能降价1.5元.
24.【解答】解:(1)由题意可得:,
∴,代入,
得:,
∴;
(2)对于,
当x=0时,y=﹣2,当y=0时,,解得,x=8,
∴A(8,0),B(0,﹣2),
∵直线把△AOB分成面积相等的两部分,
设△AOB三边OA、OB、AB的中点分别为E,F,G,则有:
E(4,0),F(0,﹣1),即G(4,﹣1),
设直线BE的解析式为y=k1x+b,
把B(0,﹣2),E(4,0)代入y=k1x+b,得:
,
解得,
∴直;
同理可求直线AF的解析式为;直线OG的解析式为;
如图,
25.【解答】解:(1)当a=﹣1,b=﹣1时,分式方程为,,
∵,
∴①[﹣1,﹣1]不是关于x的分式方程的“关联数对”;
当a=3,b=4时,分式方程为,
解得:x=1,
∵,
∴②[3,4]不是关于x的分式方程的“关联数对”;
当a=2,b=﹣5时,分式方程为,
解得,
∵,
∴③[2,﹣5]是关于x的分式方程的“关联数对”;
当a=1,b=1时,分式方程为,
此方程无解,
∴④[1,1]是关于x的分式方程的“关联数对”;
故答案为:①×;②×;③√;④×.
(2)∵数对[n2﹣3,﹣n2]是关于x的分式方程的“关联数对”,
∴,
解得:,
∴,
解得;
(3)∵数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,
∴,,
∴m(m﹣k)+1=k,
解得,
∵可化为k(m+1)x﹣m(m+1)+(m+1)=﹣2mx,
∴(m+1)2x=(m+1)(m﹣1),
解得:,
∵方程有整数解,
∴整数m+1=±1,±2,即m=0,﹣2,1,﹣3,
又m≠0,k≠1,
∴m+1≠m2+1
∴m=﹣2,﹣3.
21世纪教育网(www.21cnjy.com)
同课章节目录
