北师大版2024—2025学年七年级下册数学期末复习综合训练(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下册数学期末复习综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 642.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 21:28:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年七年级下册数学期末复习综合训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图案中,是轴对称图形的是( )
A. B. C. D.
2.下列图象中,表示y是x的函数的个数的有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法中正确的是( )
A.不相交的两条直线是平行线
B.同一平面内,不相交的两条射线叫作平行线
C.同一平面内,两条直线不相交就重合
D.同一平面内,无公共点的两条直线是平行线
4.现有两根长度分别为3cm和5cm的小棒,再从5根长度分别为2cm,3cm,4cm,5cm,8cm小棒中随机选择一根,能围成三角形的概率是( )
A. B. C. D.
5.下列算式能用平方差公式计算的是( )
A.(2a+b)(2b﹣a) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(﹣3x+y) D.(﹣x﹣y)(﹣x+y)
6.已知a1,a2, ,a2025都是正数,设M=(a1+a2+ +a2024)(a2+a3 +a2025),N=(a1+a2+ +a2025)(a2+a3 +a2024),那么M与N的大小关系是( )
A.M<N B.M=N C.M>N D.不确定
7.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
8.若将(2x+a)(2x﹣b)展开的结果中不含有x项,则a,b满足的关系式是( )
A.ab=1 B.ab=0 C.a﹣b=0 D.a+b=0
9.如果x3,那么x2( )
A.5 B.7 C.9 D.11
10.观察下列各式及其展开式
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
请你猜想(2x﹣1)8的展开式中含x2项的系数是( )
A.224 B.180 C.112 D.48
二、填空题(每小题3分,满分18分)
11.李老师将1个黑球和若干个白球(球除颜色外其他均相同)放入一个不透明的口袋并搅拌均匀,让学生进行摸球试验,学生每次从中随机摸出一个球,记下颜色后放回.重复该试验,得到如下表所示的一组统计数据:
摸球的次数n 100 300 500 800 1000
摸到黑球的次数m 23 81 130 204 250
摸到黑球的频率 0.23 0.27 0.26 0.255 0.25
根据表中数据估计袋中白球有 个.
12.x2+mx+4是关于x的完全平方式,则m= .
13.已知三角形两边的长分别为1cm,5cm,第三边长为整数,则第三边的长为 .
14.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置点A、B分别落在直线m、n上.若∠1=70°,则∠2的度数为 .
15.如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=60°,∠C=40°,则∠DAE= 度.
16.如图,在△ABC中,∠ACB=90°,∠A=26°,点D是AC边上一动点,将△ABD沿直线BD翻折,使点A落在点F处,连接BF,交AC于点E,当△DEF是直角三角形时,则∠BDC的度数为 .
北师大版2024—2025学年七年级下册数学期末复习综合训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:[(2a+3b)(2a﹣3b)﹣(2a﹣b)2﹣3ab]÷(﹣2b),其中a=2,b=﹣1.
18.计算:
(1); (2)(3x2y)2 (﹣2xy3)÷(﹣6x4y5).
19.如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图所示,四边形ABCD就是一个“格点四边形”.
(1)作出四边形ABCD关于直线BD对称的四边形A′B′C′D′;
(2)四边形ABCD的面积为 .
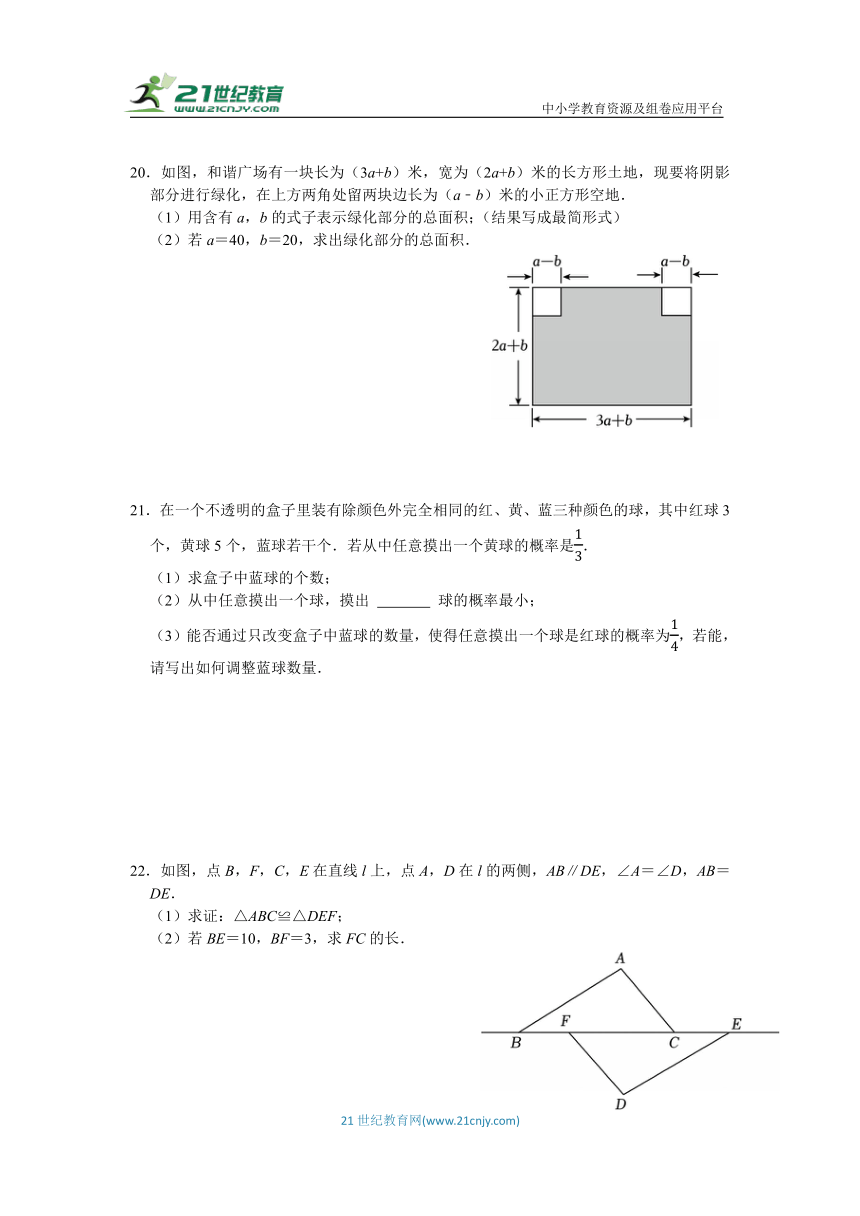
20.如图,和谐广场有一块长为(3a+b)米,宽为(2a+b)米的长方形土地,现要将阴影部分进行绿化,在上方两角处留两块边长为(a﹣b)米的小正方形空地.
(1)用含有a,b的式子表示绿化部分的总面积;(结果写成最简形式)
(2)若a=40,b=20,求出绿化部分的总面积.
21.在一个不透明的盒子里装有除颜色外完全相同的红、黄、蓝三种颜色的球,其中红球3个,黄球5个,蓝球若干个.若从中任意摸出一个黄球的概率是.
(1)求盒子中蓝球的个数;
(2)从中任意摸出一个球,摸出 球的概率最小;
(3)能否通过只改变盒子中蓝球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整蓝球数量.
22.如图,点B,F,C,E在直线l上,点A,D在l的两侧,AB∥DE,∠A=∠D,AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=10,BF=3,求FC的长.
23.已知计算:
(1)的值;
(2)的值;
(3)之间的数量关系.
24.如图1,两个正方形、的边长分别是、,将这两个正方形分别按不同的方式摆放,回答下列问题:
(1)如图2,将两个正方形叠合摆放,点与点重合,点、分别在、上,并将不重叠的阴影部分沿虚线剪开,重新拼接后,得到一个长方形,用两种不同的方法表示阴影部分面积,可以验证等式_______________.
A. B.
C. D.
(2)如图3,将两个正方形如图摆放,点与点重合,点在上,连接,若它们边长之和为14,面积之和为100,求阴影部分面积.
(3)如图4,将两个正方形如图摆放,点与点重合,点、分别在、的延长线上,若它们边长之和为14,阴影部分面积为45,求这两个正方形的面积之差.
25.定义:若多项式,,满足(其中,,是常数,且),则称多项式,,为“和谐多项式群”,常数叫做多项式,,的“和谐值”.例如多项式,,满足,那么多项式,,叫做“和谐多项式群”,常数1叫做多项式,,的“和谐值”.
(1)试判定多项式,,是否是“和谐多项式群”?若是,求出“和谐值”;若不是,请说明理由;
(2)若多项式,,为“和谐多项式群”(其中,,是常数,且),“和谐值”为.
①试说明,,满足的数量关系;
②设,试说明:;
(3),,为“和谐多项式群”,,满足且(,为常数),“和谐值”为,求出所有符合条件的,的值.
参考答案
一、选择题
1—10:ABDCD CBCDC
二、填空题
11.【解答】解:设袋中白球有x个,
由表中数据估计从口袋中随机摸出一个球是黑球的概率约为0.25,
则,
解得x=3,
经检验,x=3是所列分式方程的解.
故答案为:3.
12.【解答】解:∵x2+mx+4是关于x的完全平方式,
∴m=±2×2=±4,
故答案为:±4.
13.【解答】解:设第三边的长为x cm,
∴5﹣1<x<5+1,
∴4<x<6,
∵第三边长为整数,
∴第三边的长为5cm.
故答案为:5cm.
14.【解答】解:如图:
∵m∥n,
∴∠ABD=∠1=70°,
∴∠2=70°﹣30°=40°.
故答案为:40°.
15.【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
又∵AE平分∠BAC,
∴∠BAE∠BAC80°=40°.
∵AD是BC上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10.
16.【解答】解:由翻折得∠F=∠A=26°,∠ABD=∠EBD,
当△DEF为直角三角形,且∠EDF=90°时,如图1,
∴∠DEF=90°﹣∠F=90°﹣26°=64°,
∴∠ABE=∠DEF﹣∠F=64°﹣26°=38°,
∴,
∴∠BDC=∠ABD+∠A=19°+26°=45°;
当△DEF为直角三角形,且∠DEF=90° 时,如图2,此时点E与点C重合,
∴∠DEB=90°,且BE,CF共线,
∵∠ABE=90°﹣∠A=90°﹣26°=64°
∴,
∴∠BDC=90°﹣∠DBE=90°﹣32°=58°,
综上所述:∠BCD的度数为45°或58°,
故答案为:45°或58°.
三、解答题
17.【解答】解:原式=[4a2﹣9b2﹣(4a2﹣4ab+b2)﹣3ab]÷(﹣2b)
=(4a2﹣9b2﹣4a2+4ab﹣b2﹣3ab)÷(﹣2b)
=(﹣10b2+ab)÷(﹣2b)
=5ba,
当a=2,b=﹣1时,
原式=5×(﹣1)2
=﹣5﹣1
=﹣6.
18.【解答】解:(1)原式=﹣8+9﹣1
=0;
(2)原式=9x4y2 (﹣2xy3)÷(﹣6x4y5)
=﹣18x5y5÷(﹣6x4y5)
=3x.
19.【解答】解:(1)如图所示,四边形A′B′C′D′即为所求;
(2),
故答案为:12.
20.【解答】解:(1)用含有a,b的式子表示绿化部分的总面积=(3a+b)(2a+b)﹣2(a﹣b)2
=6a2+5ab+b2﹣2(a2﹣2ab+b2)
=6a2+5ab+b2﹣2a2+4ab﹣2b2
=(4a2+9ab﹣b2)平方米.
答:用含有a,b的式子表示绿化部分的总面积为(4a2+9ab﹣b2)平方米.
(2)当a=40,b=20时,
4a2+9ab﹣b2=4×402+9×40×20﹣202=13200(平方米).
答:绿化部分的总面积为13200平方米.
21.【解答】解:(1)由题意知,盒子中篮球的个数为5(3+5)=7(个);
(2)由题意知,盒子中红球个数为3,黄球个数为5,篮球个数为7,红球的个数最少,
所以从中任意摸出一个球,摸出红球的概率最小,
故答案为:红;
(3)∵任意摸出一个球是红球的概率为,
∴此时盒子中球的总个数为312(个),
则需要减少篮球3个.
22.【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA);
(2)解:∵△ABC≌△DEF,
∴BC=EF.
∴BF=EC.
∵BE=10,BF=3,
∴FC=BE﹣BF﹣EC=4.
23.【解答】(1)解:.
(2)解:.
(3)解:因为,
所以
因为,
所以
所以.
24.【解答】(1)解:由图2可得,
拼接后阴影部分面积为,
拼接前阴影部分面积为,
拼接前后,阴影部分面积相等,
故选:C.
(2)解:由题意得,,,
,
,
阴影部分面积为.
(3)解:如图,连接,
由题意得,阴影部分面积,,
,
,
,
,
这两个正方形的面积之差为56.
25.【解答】(1)不是
它们不是“和谐多项式群”.
(2)①
,,为“和谐多项式群”
②,,为“和谐多项式群”,“和谐值”为
(3)①当时
,
,(舍)
②当时
,
解得.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年七年级下册数学期末复习综合训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图案中,是轴对称图形的是( )
A. B. C. D.
2.下列图象中,表示y是x的函数的个数的有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法中正确的是( )
A.不相交的两条直线是平行线
B.同一平面内,不相交的两条射线叫作平行线
C.同一平面内,两条直线不相交就重合
D.同一平面内,无公共点的两条直线是平行线
4.现有两根长度分别为3cm和5cm的小棒,再从5根长度分别为2cm,3cm,4cm,5cm,8cm小棒中随机选择一根,能围成三角形的概率是( )
A. B. C. D.
5.下列算式能用平方差公式计算的是( )
A.(2a+b)(2b﹣a) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(﹣3x+y) D.(﹣x﹣y)(﹣x+y)
6.已知a1,a2, ,a2025都是正数,设M=(a1+a2+ +a2024)(a2+a3 +a2025),N=(a1+a2+ +a2025)(a2+a3 +a2024),那么M与N的大小关系是( )
A.M<N B.M=N C.M>N D.不确定
7.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
8.若将(2x+a)(2x﹣b)展开的结果中不含有x项,则a,b满足的关系式是( )
A.ab=1 B.ab=0 C.a﹣b=0 D.a+b=0
9.如果x3,那么x2( )
A.5 B.7 C.9 D.11
10.观察下列各式及其展开式
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
请你猜想(2x﹣1)8的展开式中含x2项的系数是( )
A.224 B.180 C.112 D.48
二、填空题(每小题3分,满分18分)
11.李老师将1个黑球和若干个白球(球除颜色外其他均相同)放入一个不透明的口袋并搅拌均匀,让学生进行摸球试验,学生每次从中随机摸出一个球,记下颜色后放回.重复该试验,得到如下表所示的一组统计数据:
摸球的次数n 100 300 500 800 1000
摸到黑球的次数m 23 81 130 204 250
摸到黑球的频率 0.23 0.27 0.26 0.255 0.25
根据表中数据估计袋中白球有 个.
12.x2+mx+4是关于x的完全平方式,则m= .
13.已知三角形两边的长分别为1cm,5cm,第三边长为整数,则第三边的长为 .
14.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置点A、B分别落在直线m、n上.若∠1=70°,则∠2的度数为 .
15.如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=60°,∠C=40°,则∠DAE= 度.
16.如图,在△ABC中,∠ACB=90°,∠A=26°,点D是AC边上一动点,将△ABD沿直线BD翻折,使点A落在点F处,连接BF,交AC于点E,当△DEF是直角三角形时,则∠BDC的度数为 .
北师大版2024—2025学年七年级下册数学期末复习综合训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:[(2a+3b)(2a﹣3b)﹣(2a﹣b)2﹣3ab]÷(﹣2b),其中a=2,b=﹣1.
18.计算:
(1); (2)(3x2y)2 (﹣2xy3)÷(﹣6x4y5).
19.如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图所示,四边形ABCD就是一个“格点四边形”.
(1)作出四边形ABCD关于直线BD对称的四边形A′B′C′D′;
(2)四边形ABCD的面积为 .
20.如图,和谐广场有一块长为(3a+b)米,宽为(2a+b)米的长方形土地,现要将阴影部分进行绿化,在上方两角处留两块边长为(a﹣b)米的小正方形空地.
(1)用含有a,b的式子表示绿化部分的总面积;(结果写成最简形式)
(2)若a=40,b=20,求出绿化部分的总面积.
21.在一个不透明的盒子里装有除颜色外完全相同的红、黄、蓝三种颜色的球,其中红球3个,黄球5个,蓝球若干个.若从中任意摸出一个黄球的概率是.
(1)求盒子中蓝球的个数;
(2)从中任意摸出一个球,摸出 球的概率最小;
(3)能否通过只改变盒子中蓝球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整蓝球数量.
22.如图,点B,F,C,E在直线l上,点A,D在l的两侧,AB∥DE,∠A=∠D,AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=10,BF=3,求FC的长.
23.已知计算:
(1)的值;
(2)的值;
(3)之间的数量关系.
24.如图1,两个正方形、的边长分别是、,将这两个正方形分别按不同的方式摆放,回答下列问题:
(1)如图2,将两个正方形叠合摆放,点与点重合,点、分别在、上,并将不重叠的阴影部分沿虚线剪开,重新拼接后,得到一个长方形,用两种不同的方法表示阴影部分面积,可以验证等式_______________.
A. B.
C. D.
(2)如图3,将两个正方形如图摆放,点与点重合,点在上,连接,若它们边长之和为14,面积之和为100,求阴影部分面积.
(3)如图4,将两个正方形如图摆放,点与点重合,点、分别在、的延长线上,若它们边长之和为14,阴影部分面积为45,求这两个正方形的面积之差.
25.定义:若多项式,,满足(其中,,是常数,且),则称多项式,,为“和谐多项式群”,常数叫做多项式,,的“和谐值”.例如多项式,,满足,那么多项式,,叫做“和谐多项式群”,常数1叫做多项式,,的“和谐值”.
(1)试判定多项式,,是否是“和谐多项式群”?若是,求出“和谐值”;若不是,请说明理由;
(2)若多项式,,为“和谐多项式群”(其中,,是常数,且),“和谐值”为.
①试说明,,满足的数量关系;
②设,试说明:;
(3),,为“和谐多项式群”,,满足且(,为常数),“和谐值”为,求出所有符合条件的,的值.
参考答案
一、选择题
1—10:ABDCD CBCDC
二、填空题
11.【解答】解:设袋中白球有x个,
由表中数据估计从口袋中随机摸出一个球是黑球的概率约为0.25,
则,
解得x=3,
经检验,x=3是所列分式方程的解.
故答案为:3.
12.【解答】解:∵x2+mx+4是关于x的完全平方式,
∴m=±2×2=±4,
故答案为:±4.
13.【解答】解:设第三边的长为x cm,
∴5﹣1<x<5+1,
∴4<x<6,
∵第三边长为整数,
∴第三边的长为5cm.
故答案为:5cm.
14.【解答】解:如图:
∵m∥n,
∴∠ABD=∠1=70°,
∴∠2=70°﹣30°=40°.
故答案为:40°.
15.【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
又∵AE平分∠BAC,
∴∠BAE∠BAC80°=40°.
∵AD是BC上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10.
16.【解答】解:由翻折得∠F=∠A=26°,∠ABD=∠EBD,
当△DEF为直角三角形,且∠EDF=90°时,如图1,
∴∠DEF=90°﹣∠F=90°﹣26°=64°,
∴∠ABE=∠DEF﹣∠F=64°﹣26°=38°,
∴,
∴∠BDC=∠ABD+∠A=19°+26°=45°;
当△DEF为直角三角形,且∠DEF=90° 时,如图2,此时点E与点C重合,
∴∠DEB=90°,且BE,CF共线,
∵∠ABE=90°﹣∠A=90°﹣26°=64°
∴,
∴∠BDC=90°﹣∠DBE=90°﹣32°=58°,
综上所述:∠BCD的度数为45°或58°,
故答案为:45°或58°.
三、解答题
17.【解答】解:原式=[4a2﹣9b2﹣(4a2﹣4ab+b2)﹣3ab]÷(﹣2b)
=(4a2﹣9b2﹣4a2+4ab﹣b2﹣3ab)÷(﹣2b)
=(﹣10b2+ab)÷(﹣2b)
=5ba,
当a=2,b=﹣1时,
原式=5×(﹣1)2
=﹣5﹣1
=﹣6.
18.【解答】解:(1)原式=﹣8+9﹣1
=0;
(2)原式=9x4y2 (﹣2xy3)÷(﹣6x4y5)
=﹣18x5y5÷(﹣6x4y5)
=3x.
19.【解答】解:(1)如图所示,四边形A′B′C′D′即为所求;
(2),
故答案为:12.
20.【解答】解:(1)用含有a,b的式子表示绿化部分的总面积=(3a+b)(2a+b)﹣2(a﹣b)2
=6a2+5ab+b2﹣2(a2﹣2ab+b2)
=6a2+5ab+b2﹣2a2+4ab﹣2b2
=(4a2+9ab﹣b2)平方米.
答:用含有a,b的式子表示绿化部分的总面积为(4a2+9ab﹣b2)平方米.
(2)当a=40,b=20时,
4a2+9ab﹣b2=4×402+9×40×20﹣202=13200(平方米).
答:绿化部分的总面积为13200平方米.
21.【解答】解:(1)由题意知,盒子中篮球的个数为5(3+5)=7(个);
(2)由题意知,盒子中红球个数为3,黄球个数为5,篮球个数为7,红球的个数最少,
所以从中任意摸出一个球,摸出红球的概率最小,
故答案为:红;
(3)∵任意摸出一个球是红球的概率为,
∴此时盒子中球的总个数为312(个),
则需要减少篮球3个.
22.【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA);
(2)解:∵△ABC≌△DEF,
∴BC=EF.
∴BF=EC.
∵BE=10,BF=3,
∴FC=BE﹣BF﹣EC=4.
23.【解答】(1)解:.
(2)解:.
(3)解:因为,
所以
因为,
所以
所以.
24.【解答】(1)解:由图2可得,
拼接后阴影部分面积为,
拼接前阴影部分面积为,
拼接前后,阴影部分面积相等,
故选:C.
(2)解:由题意得,,,
,
,
阴影部分面积为.
(3)解:如图,连接,
由题意得,阴影部分面积,,
,
,
,
,
这两个正方形的面积之差为56.
25.【解答】(1)不是
它们不是“和谐多项式群”.
(2)①
,,为“和谐多项式群”
②,,为“和谐多项式群”,“和谐值”为
(3)①当时
,
,(舍)
②当时
,
解得.
21世纪教育网(www.21cnjy.com)
同课章节目录
