北师大版2024—2025学年七年级下学期数学期末复习强化提分练习(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下学期数学期末复习强化提分练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 665.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 21:19:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年七年级下学期数学期末复习强化提分练习
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图案中,是轴对称图形的是( )
A. B. C. D.
2.芯片内部有数以亿计的晶体管,为追求更高质量的芯片和更低的电力功耗,需要设计体积更小的晶体管.某芯片的晶体管栅极的宽度为0.0000014cm.将数据0.0000014用科学记数法表示为( )
A.14×10﹣7 B.1.4×10﹣6 C.0.14×10﹣5 D.1.4×10﹣5
3.计算的结果是( )
A. B. C. D.
4.下面的图象中,可以大致刻画匀速行驶的汽车的速度随时间变化情况的是( )
A. B. C. D.
5.如果事件A发生的概率是,那么在相同条件下重复试验,下列说法正确的是( )
A.做200次这种试验,事件A必发生1次B.做200次这种试验,事件A发生的频率是
C.做200次这种试验,事件A可能发生1次
D.做200次这种试验,前199次事件A没发生,最后1次事件A才发生
6.若是正整数,且满足,则与的关系正确的是
A. B. C. D.
7.如果的乘积中不含x的一次项,则m为( )
A. B.3 C. D.
8.如表是一位同学在罚球线上投篮的试验结果,根据表中数据回答下列问题:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 124 153 252
估计这位同学投篮一次,投中的概率约是( )(精确到0.1)
A.0.4 B.0.5 C.0.55 D.0.6
9.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
10.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,AB=8cm,点P从B出发,沿折线BE﹣ED﹣DC匀速运动,运动到点C停止,P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的关系图象如图②,则a、b的值分别为( )
A.6,10 B.6,11 C.7,11 D.7,12
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.某书店对外租赁图书,收费办法是:每本书在租赁后的头两天每天按0.5元收费,以后每天按0.7元收费(不足一天按一天计算)(元)和租赁天数(x≥2)之间的关系式为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
16.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
第II卷
北师大版2024—2025学年七年级下学期数学期末复习强化提分练习
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值,其中.
18.计算:.
19.为了调查学生对海南自贸港建设知识的了解程度,普及海南自贸港建设的相关知识.某校随机抽取若干名学生进行了测试,根据测试成绩分布情况,他们将全部测试成绩分成A,B,C,D四组,绘制了如下不完整的统计图表:
问卷测试成绩统计表:
组别 分数/分
A 60<x≤70
B 70<x≤80
C 80<x≤90
D 90<x≤100
(1)本次调查采用的调查方式为 (填写“普查”或“抽样调查”);
(2)在这次调查中,抽取的学生一共有 人;扇形统计图中n的值为 ;
(3)样本的D组50名学生中有20名男生和30名女生.若从这50名学生中随机抽取1名学生代表学校参加市里的演讲比赛,则恰好抽到女生的概率是 ;
(4)若该校共有1000名学生参加测试,则估计问卷测试成绩在80<x≤90之间的学生有 人.
20.在计算(2x+a)(x+b)时,甲错把b看成了6,得到结果是:2x2+8x﹣24;乙错把a看成了﹣a,得到结果:2x2+14x+20.
(1)求出a,b的值;
(2)在(1)的条件下,计算(2x+a)(x+b)的结果.
21.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
(1)求∠APB度数;
(2)求证:△ABP≌△FBP;
(3)求证:AH+BD=AB.
22.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
23.已知ab=2,ac=4,ak=32(a≠0).
(1)求a2b+2c﹣k的值;
(2)求k﹣3b﹣c的值.
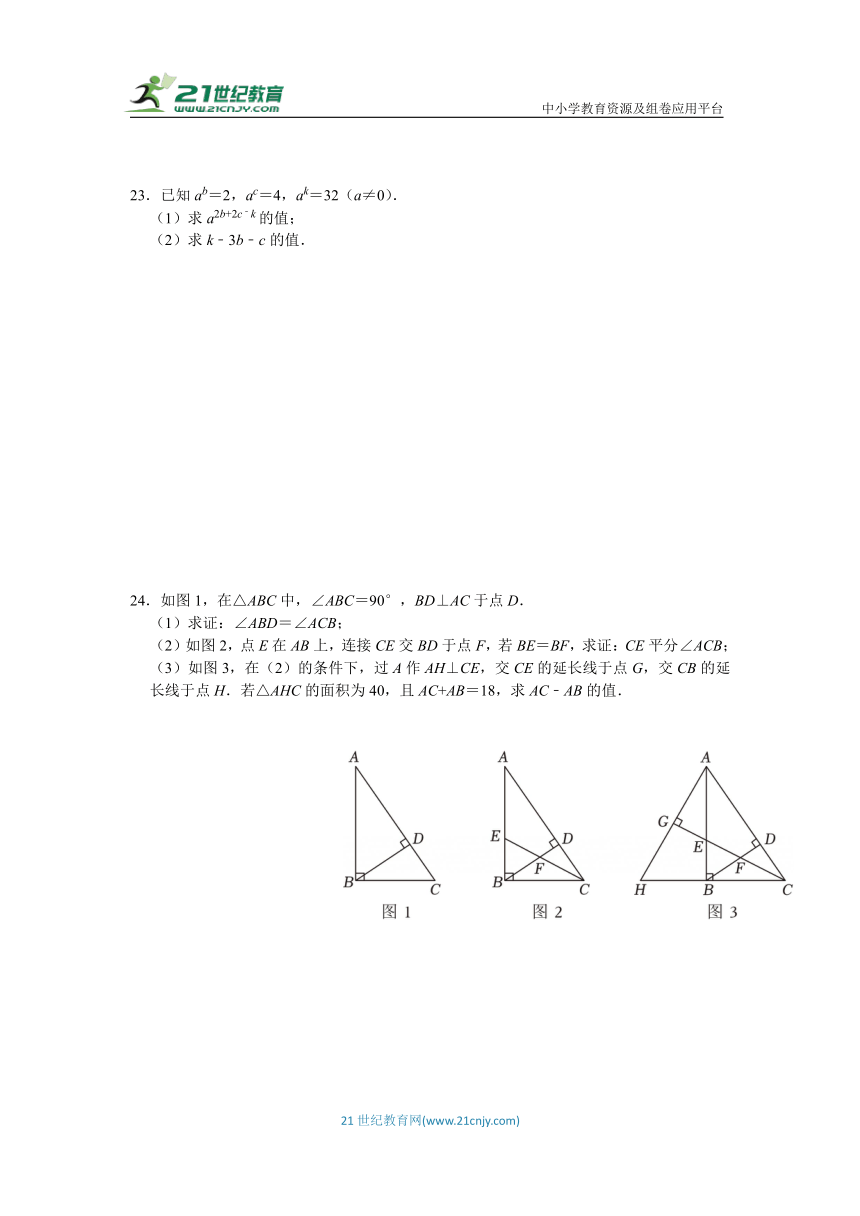
24.如图1,在△ABC中,∠ABC=90°,BD⊥AC于点D.
(1)求证:∠ABD=∠ACB;
(2)如图2,点E在AB上,连接CE交BD于点F,若BE=BF,求证:CE平分∠ACB;
(3)如图3,在(2)的条件下,过A作AH⊥CE,交CE的延长线于点G,交CB的延长线于点H.若△AHC的面积为40,且AC+AB=18,求AC﹣AB的值.
25.如图1,点分别在直线和上,,射线从射线的位置开始,绕点以每秒的速度逆时针旋转,同时射线从射线的位置开始,绕点以每秒的速度逆时针旋转,射线旋转到的位置时,两者停止运动.设旋转时间为秒.
(1)①的度数为___________(用的代数式表示);
②当射线经过点时,此时的度数为____________.
(2)在转动过程中,是否存在某个时刻,使得射线与射线所在直线的夹角为?若存在,求出的值;若不存在,请说明理由.
(3)在转动过程中,若射线与射线交于点,过点作交直线于点,与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
参考答案
一、选择题
1—10:ABAAB BBBDC
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:y与x的关系式为y=45﹣6x.
故答案为:y=45﹣6x.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
故答案为:15.
14.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
15.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
16.【解答】解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=6,BP=CQ时,△BPE与△CQP全等,
此时,6=8﹣3t,
解得t,
∴BP=CQ=2,
此时,点Q的运动速度为23厘米/秒;
②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t,
∴点Q的运动速度为6厘米/秒;
故答案为:3或.
三、解答题
17.【解答】解:
=(4a2+4ab+b2﹣3a2+4ab﹣b2﹣a)÷(a)
=(a2+8ab﹣a)÷(a)
=﹣2a﹣16b+2,
当时,原式=﹣2×(﹣1)﹣162
=2﹣8+2
=﹣4.
18.【解答】解:原式=4+1﹣3
=5﹣3
=2.
19.【解答】解:(1)∵某校随机抽取若干名学生进行了测试,
∴本次调查采用的调查方式为抽样调查,
故答案为:抽样调查;
(2)20÷10%=200人,
∴在这次调查中,抽取的学生一共有200人,
∴,
∴n=35,
故答案为:200;35;
(3),
∴从这50名学生中随机抽取1名学生代表学校参加市里的演讲比赛,则恰好抽到女生的概率是,
故答案为:;
(4)1000×35%=350人,
∴估计估计问卷测试成绩在80<x≤90之间的学生有350人,
故答案为:350.
20.【解答】解:(1)甲错把b看成了6,
(2x+a)(x+6)
=2x2+12x+ax+6a
=2x2+(12+a)x+6a
=2x2+8x﹣24,
∴12+a=8,
解得:a=﹣4;
乙错把a看成了﹣a,
(2x﹣a)(x+b)
=2x2+2bx﹣ax﹣ab
=2x2+(﹣a+2b)x﹣ab
=2x2+14x+20,
∴2b﹣a=14,
把a=﹣4代入,得b=5;
(2)当a=﹣4,b=5时,
(2x+a)(x+b)
=(2x﹣4)(x+5)
=2x2+10x﹣4x﹣20
=2x2+6x﹣20.
21.【解答】解:(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA(∠ABC+∠BAC)=45°,
∴∠APB=180°﹣45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
22.【解答】(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
23.【解答】解:(1)∵ab=2,ac=4,ak=32,
∴a2b+2c﹣k
=a2b a2c÷ak
=(ab)2 (ac)2÷ak
=22×42÷32
=4×16÷32
=2;
(2)ak﹣3b﹣c
=ak÷a3b÷ac
=ak÷(ab)3÷ac
=32÷23÷4
=32÷8÷4
=1,
∵ab=2,
∴a≠±1,
∵ak﹣3b﹣c=1(a≠0,a≠±1),
∴k﹣3b﹣c=0.
24.【解答】(1)证明:∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
∵BD⊥AC,
∴∠ACB+∠CBD=90°,
∴∠ABD=∠ACB;
(2)证明:同(1)的方法可得:∠A=∠CBD,
∵BE=BF,
∴∠BEF=∠BFE,
∵∠BEF=∠A+∠ACE,∠BFE=∠CBD+∠BCE,
∴∠ACE=∠BCE,
∴CE平分∠ACB;
(3)解:在△ACG和△HCG中,
,
∴△ACG≌△HCG(ASA),
∴AC=CH,
∵△AHC的面积为40,
∴AB HC=40,
∴2AB HC=160,
∴2AB AC=160,
∵AC+AB=18,
∴(AC+AB)2=324,
∴AC2+2AB AC+AB2=324,
∴AC2﹣2AB AC+AB2=4,
∴(AC﹣AB)2=4,
∴AC﹣AB=2.
25.【解答】解:(1)解:①如图,
∵射线从射线的位置开始,绕点以每秒的速度逆时针旋转,
∴
故答案为:;
②如图:
∵
∴
∴,
解得:,
∴
∴
故答案为:.
(2)解:当射线与射线的反向延长线相交于G,且时 ,如图,
∵
∴
∵,
∴
解得:;
当射线与射线相交于G,且时,如图,
∵,,
∴
解得:(不符合题意,舍去);
当射线与射线相交于G,且时,如图,
∵
∴
解得:;
综上,存在,射线与射线所在直线的夹角为,t值为秒或秒.
(3)解:与的数量关系要发生变化.
理由:当时,射线与射线交于点,如图,
∵
∴
∵,,
∴
∴
∴
∴与的数量关系要随着t的发生而变化.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年七年级下学期数学期末复习强化提分练习
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图案中,是轴对称图形的是( )
A. B. C. D.
2.芯片内部有数以亿计的晶体管,为追求更高质量的芯片和更低的电力功耗,需要设计体积更小的晶体管.某芯片的晶体管栅极的宽度为0.0000014cm.将数据0.0000014用科学记数法表示为( )
A.14×10﹣7 B.1.4×10﹣6 C.0.14×10﹣5 D.1.4×10﹣5
3.计算的结果是( )
A. B. C. D.
4.下面的图象中,可以大致刻画匀速行驶的汽车的速度随时间变化情况的是( )
A. B. C. D.
5.如果事件A发生的概率是,那么在相同条件下重复试验,下列说法正确的是( )
A.做200次这种试验,事件A必发生1次B.做200次这种试验,事件A发生的频率是
C.做200次这种试验,事件A可能发生1次
D.做200次这种试验,前199次事件A没发生,最后1次事件A才发生
6.若是正整数,且满足,则与的关系正确的是
A. B. C. D.
7.如果的乘积中不含x的一次项,则m为( )
A. B.3 C. D.
8.如表是一位同学在罚球线上投篮的试验结果,根据表中数据回答下列问题:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 124 153 252
估计这位同学投篮一次,投中的概率约是( )(精确到0.1)
A.0.4 B.0.5 C.0.55 D.0.6
9.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
10.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,AB=8cm,点P从B出发,沿折线BE﹣ED﹣DC匀速运动,运动到点C停止,P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的关系图象如图②,则a、b的值分别为( )
A.6,10 B.6,11 C.7,11 D.7,12
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.某书店对外租赁图书,收费办法是:每本书在租赁后的头两天每天按0.5元收费,以后每天按0.7元收费(不足一天按一天计算)(元)和租赁天数(x≥2)之间的关系式为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
16.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
第II卷
北师大版2024—2025学年七年级下学期数学期末复习强化提分练习
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值,其中.
18.计算:.
19.为了调查学生对海南自贸港建设知识的了解程度,普及海南自贸港建设的相关知识.某校随机抽取若干名学生进行了测试,根据测试成绩分布情况,他们将全部测试成绩分成A,B,C,D四组,绘制了如下不完整的统计图表:
问卷测试成绩统计表:
组别 分数/分
A 60<x≤70
B 70<x≤80
C 80<x≤90
D 90<x≤100
(1)本次调查采用的调查方式为 (填写“普查”或“抽样调查”);
(2)在这次调查中,抽取的学生一共有 人;扇形统计图中n的值为 ;
(3)样本的D组50名学生中有20名男生和30名女生.若从这50名学生中随机抽取1名学生代表学校参加市里的演讲比赛,则恰好抽到女生的概率是 ;
(4)若该校共有1000名学生参加测试,则估计问卷测试成绩在80<x≤90之间的学生有 人.
20.在计算(2x+a)(x+b)时,甲错把b看成了6,得到结果是:2x2+8x﹣24;乙错把a看成了﹣a,得到结果:2x2+14x+20.
(1)求出a,b的值;
(2)在(1)的条件下,计算(2x+a)(x+b)的结果.
21.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
(1)求∠APB度数;
(2)求证:△ABP≌△FBP;
(3)求证:AH+BD=AB.
22.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
23.已知ab=2,ac=4,ak=32(a≠0).
(1)求a2b+2c﹣k的值;
(2)求k﹣3b﹣c的值.
24.如图1,在△ABC中,∠ABC=90°,BD⊥AC于点D.
(1)求证:∠ABD=∠ACB;
(2)如图2,点E在AB上,连接CE交BD于点F,若BE=BF,求证:CE平分∠ACB;
(3)如图3,在(2)的条件下,过A作AH⊥CE,交CE的延长线于点G,交CB的延长线于点H.若△AHC的面积为40,且AC+AB=18,求AC﹣AB的值.
25.如图1,点分别在直线和上,,射线从射线的位置开始,绕点以每秒的速度逆时针旋转,同时射线从射线的位置开始,绕点以每秒的速度逆时针旋转,射线旋转到的位置时,两者停止运动.设旋转时间为秒.
(1)①的度数为___________(用的代数式表示);
②当射线经过点时,此时的度数为____________.
(2)在转动过程中,是否存在某个时刻,使得射线与射线所在直线的夹角为?若存在,求出的值;若不存在,请说明理由.
(3)在转动过程中,若射线与射线交于点,过点作交直线于点,与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
参考答案
一、选择题
1—10:ABAAB BBBDC
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:y与x的关系式为y=45﹣6x.
故答案为:y=45﹣6x.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
故答案为:15.
14.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
15.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
16.【解答】解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=6,BP=CQ时,△BPE与△CQP全等,
此时,6=8﹣3t,
解得t,
∴BP=CQ=2,
此时,点Q的运动速度为23厘米/秒;
②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t,
∴点Q的运动速度为6厘米/秒;
故答案为:3或.
三、解答题
17.【解答】解:
=(4a2+4ab+b2﹣3a2+4ab﹣b2﹣a)÷(a)
=(a2+8ab﹣a)÷(a)
=﹣2a﹣16b+2,
当时,原式=﹣2×(﹣1)﹣162
=2﹣8+2
=﹣4.
18.【解答】解:原式=4+1﹣3
=5﹣3
=2.
19.【解答】解:(1)∵某校随机抽取若干名学生进行了测试,
∴本次调查采用的调查方式为抽样调查,
故答案为:抽样调查;
(2)20÷10%=200人,
∴在这次调查中,抽取的学生一共有200人,
∴,
∴n=35,
故答案为:200;35;
(3),
∴从这50名学生中随机抽取1名学生代表学校参加市里的演讲比赛,则恰好抽到女生的概率是,
故答案为:;
(4)1000×35%=350人,
∴估计估计问卷测试成绩在80<x≤90之间的学生有350人,
故答案为:350.
20.【解答】解:(1)甲错把b看成了6,
(2x+a)(x+6)
=2x2+12x+ax+6a
=2x2+(12+a)x+6a
=2x2+8x﹣24,
∴12+a=8,
解得:a=﹣4;
乙错把a看成了﹣a,
(2x﹣a)(x+b)
=2x2+2bx﹣ax﹣ab
=2x2+(﹣a+2b)x﹣ab
=2x2+14x+20,
∴2b﹣a=14,
把a=﹣4代入,得b=5;
(2)当a=﹣4,b=5时,
(2x+a)(x+b)
=(2x﹣4)(x+5)
=2x2+10x﹣4x﹣20
=2x2+6x﹣20.
21.【解答】解:(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA(∠ABC+∠BAC)=45°,
∴∠APB=180°﹣45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
22.【解答】(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
23.【解答】解:(1)∵ab=2,ac=4,ak=32,
∴a2b+2c﹣k
=a2b a2c÷ak
=(ab)2 (ac)2÷ak
=22×42÷32
=4×16÷32
=2;
(2)ak﹣3b﹣c
=ak÷a3b÷ac
=ak÷(ab)3÷ac
=32÷23÷4
=32÷8÷4
=1,
∵ab=2,
∴a≠±1,
∵ak﹣3b﹣c=1(a≠0,a≠±1),
∴k﹣3b﹣c=0.
24.【解答】(1)证明:∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
∵BD⊥AC,
∴∠ACB+∠CBD=90°,
∴∠ABD=∠ACB;
(2)证明:同(1)的方法可得:∠A=∠CBD,
∵BE=BF,
∴∠BEF=∠BFE,
∵∠BEF=∠A+∠ACE,∠BFE=∠CBD+∠BCE,
∴∠ACE=∠BCE,
∴CE平分∠ACB;
(3)解:在△ACG和△HCG中,
,
∴△ACG≌△HCG(ASA),
∴AC=CH,
∵△AHC的面积为40,
∴AB HC=40,
∴2AB HC=160,
∴2AB AC=160,
∵AC+AB=18,
∴(AC+AB)2=324,
∴AC2+2AB AC+AB2=324,
∴AC2﹣2AB AC+AB2=4,
∴(AC﹣AB)2=4,
∴AC﹣AB=2.
25.【解答】解:(1)解:①如图,
∵射线从射线的位置开始,绕点以每秒的速度逆时针旋转,
∴
故答案为:;
②如图:
∵
∴
∴,
解得:,
∴
∴
故答案为:.
(2)解:当射线与射线的反向延长线相交于G,且时 ,如图,
∵
∴
∵,
∴
解得:;
当射线与射线相交于G,且时,如图,
∵,,
∴
解得:(不符合题意,舍去);
当射线与射线相交于G,且时,如图,
∵
∴
解得:;
综上,存在,射线与射线所在直线的夹角为,t值为秒或秒.
(3)解:与的数量关系要发生变化.
理由:当时,射线与射线交于点,如图,
∵
∴
∵,,
∴
∴
∴
∴与的数量关系要随着t的发生而变化.
21世纪教育网(www.21cnjy.com)
同课章节目录
