北师大版2024—2025学年七年级下学期数学期末考试押题卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下学期数学期末考试押题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 802.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 21:15:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年七年级下学期数学期末考试押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.深圳作为科技创新之城,有很多知名品牌,以下深圳品牌标志,其中是轴对称图形的是( )
A. B. C. D.
2.“一夜秋风起,天地桂花香.”桂花是仙游县的县花,其花粉的直径约为米,将数据用科学记数法表示为( )
A. B. C. D.
3.下列事件中,是必然事件的为( )
A.天内下雨 B.打开电视机,正在播放广告
C.人中至少有人的生日相同 D.抛掷硬币,正面向上
4.全家观影已成为过年新民俗.据悉2025年春节档共有四部重磅影片上映,分别是《射雕英雄传:侠之大者》、《封神第二部:战火西岐》、《哪吒之魔童闹海》、《:重启未来》.若小明从这四部影片中随机选择一部影片观看,则选中《哪吒之魔童闹海》的概率是( )
A. B. C. D.
5.若,则m与n之间的关系为( )
A. B. C. D.
6.下列长度的三条线段,能组成三角形的是( )
A.4,4,5 B.1,3,4 C.5,6,12 D.1,6,8
7.不论为何值,等式都成立,则代数式的值为( )
A. B. C.6 D.4
8.如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠DCE D.∠D+∠1+∠3=180°
9.已知x满足(x﹣2020)(x﹣2024)=516,则(x﹣2022)2的值是( )
A.512 B.516 C.520 D.1032
10.定义,以下说法正确的有( )个.
①若不含x的二次项,则.
②若为正整数,、、为自然数,,则满足条件的整式共计有9种.
③若(i为自然数),,,则.
④若,,则.
A.0 B.1 C.2 D.3
二、填空题(每小题3分,满分18分)
11.若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .
12.如图,在△ABC中,AD平分∠BAC,DE=1,则S△ACD= .
13.二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨)(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),则抽到的节气在夏季的概率为 .
14.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置点A、B分别落在直线m、n上.若∠1=70°,则∠2的度数为 .
15.如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=60°,∠C=40°,则∠DAE= 度.
16.如图,在△ABC中,∠ACB=90°,∠A=26°,点D是AC边上一动点,将△ABD沿直线BD翻折,使点A落在点F处,连接BF,交AC于点E,当△DEF是直角三角形时,则∠BDC的度数为 .
北师大版2024—2025学年七年级下学期数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:[(2x﹣y)2﹣y(2x+y)]÷2x,其中x=2,y=﹣1.
18.已知(mx﹣3)(﹣x+n)的展开式中不含x项,且常数项是﹣3.求下列各式的值:
(1)m3+n3;
(2)(m+n)(m2﹣mn+n2).
19.已知5a=2,5b=6,5c=48.
(1)求53a的值;
(2)求5c﹣2b的值;
(3)求出字母a、b、c之间的数量关系 .
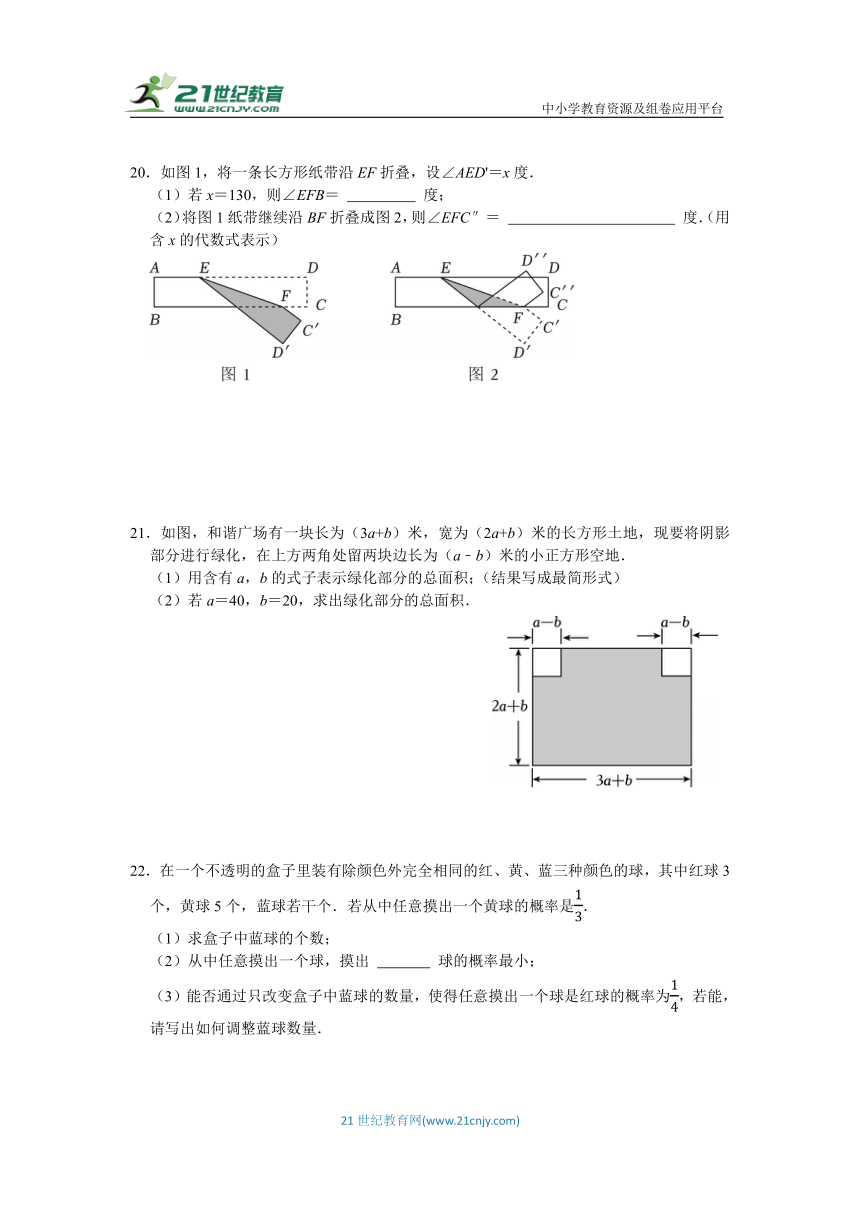
20.如图1,将一条长方形纸带沿EF折叠,设∠AED'=x度.
(1)若x=130,则∠EFB= 度;
(2)将图1纸带继续沿BF折叠成图2,则∠EFC″= 度.(用含x的代数式表示)
21.如图,和谐广场有一块长为(3a+b)米,宽为(2a+b)米的长方形土地,现要将阴影部分进行绿化,在上方两角处留两块边长为(a﹣b)米的小正方形空地.
(1)用含有a,b的式子表示绿化部分的总面积;(结果写成最简形式)
(2)若a=40,b=20,求出绿化部分的总面积.
22.在一个不透明的盒子里装有除颜色外完全相同的红、黄、蓝三种颜色的球,其中红球3个,黄球5个,蓝球若干个.若从中任意摸出一个黄球的概率是.
(1)求盒子中蓝球的个数;
(2)从中任意摸出一个球,摸出 球的概率最小;
(3)能否通过只改变盒子中蓝球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整蓝球数量.
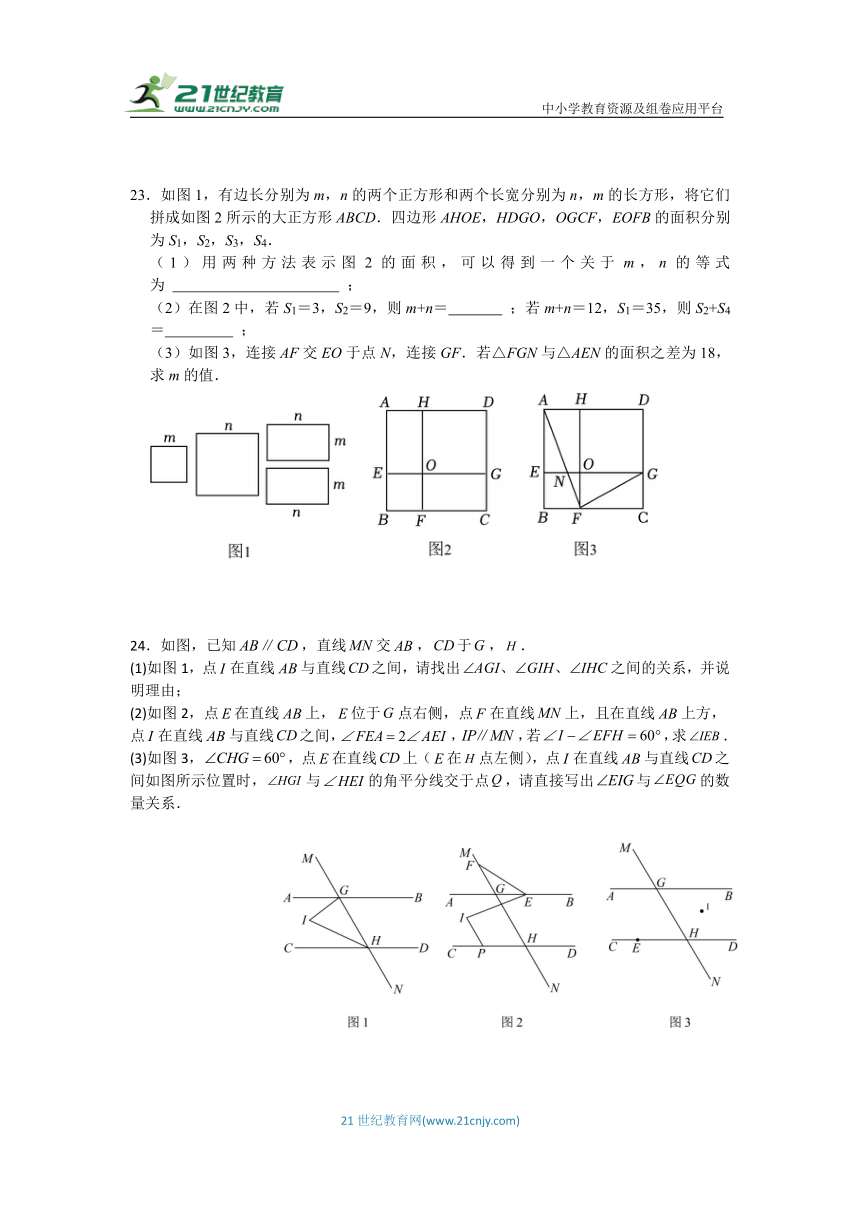
23.如图1,有边长分别为m,n的两个正方形和两个长宽分别为n,m的长方形,将它们拼成如图2所示的大正方形ABCD.四边形AHOE,HDGO,OGCF,EOFB的面积分别为S1,S2,S3,S4.
(1)用两种方法表示图2的面积,可以得到一个关于m,n的等式为 ;
(2)在图2中,若S1=3,S2=9,则m+n= ;若m+n=12,S1=35,则S2+S4= ;
(3)如图3,连接AF交EO于点N,连接GF.若△FGN与△AEN的面积之差为18,求m的值.
24.如图,已知,直线交,于,.
(1)如图1,点在直线与直线之间,请找出之间的关系,并说明理由;
(2)如图2,点在直线上,位于点右侧,点在直线上,且在直线上方,点在直线与直线之间,,,若,求.
(3)如图3,,点在直线上(在点左侧),点在直线与直线之间如图所示位置时,与的角平分线交于点,请直接写出与的数量关系.
25.定义:若多项式,,满足(其中,,是常数,且),则称多项式,,为“和谐多项式群”,常数叫做多项式,,的“和谐值”.例如多项式,,满足,那么多项式,,叫做“和谐多项式群”,常数1叫做多项式,,的“和谐值”.
(1)试判定多项式,,是否是“和谐多项式群”?若是,求出“和谐值”;若不是,请说明理由;
(2)若多项式,,为“和谐多项式群”(其中,,是常数,且),“和谐值”为.
①试说明,,满足的数量关系;
②设,试说明:;
(3),,为“和谐多项式群”,,满足且(,为常数),“和谐值”为,求出所有符合条件的,的值.
参考答案
一、选择题
1—10:ABCBD ABBCA
二、填空题
11.【解答】解:①5是腰长时,三角形的三边分别为5、3,2,
能组成三角形,
周长=5+6+2=12,
②5是底边时,三角形的三边分别为7、2、5,
不能组成三角形,
故答案为:12.
12.【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,
∴DE=DF=1,
∵AC=2,
∴S△ACD=AC DF
=×2×1
=8,
故答案为:1.
13.【解答】解:从二十四个节气中选一个节气,则抽到的节气在夏季的概率为=,
故答案为:.
14.【解答】解:如图:
∵m∥n,
∴∠ABD=∠1=70°,
∴∠2=70°﹣30°=40°.
故答案为:40°.
15.【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
又∵AE平分∠BAC,
∴∠BAE∠BAC80°=40°.
∵AD是BC上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10.
16.【解答】解:由翻折得∠F=∠A=26°,∠ABD=∠EBD,
当△DEF为直角三角形,且∠EDF=90°时,如图1,
∴∠DEF=90°﹣∠F=90°﹣26°=64°,
∴∠ABE=∠DEF﹣∠F=64°﹣26°=38°,
∴,
∴∠BDC=∠ABD+∠A=19°+26°=45°;
当△DEF为直角三角形,且∠DEF=90° 时,如图2,此时点E与点C重合,
∴∠DEB=90°,且BE,CF共线,
∵∠ABE=90°﹣∠A=90°﹣26°=64°
∴,
∴∠BDC=90°﹣∠DBE=90°﹣32°=58°,
综上所述:∠BCD的度数为45°或58°,
故答案为:45°或58°.
三、解答题
17.【解答】解:原式=(4x2﹣4xy+y2﹣2xy﹣y2)÷2x
=(4x2﹣6xy)÷2x
=2x﹣3y.
当x=2,y=﹣1时,原式=2×2﹣3×(﹣1)=7.
18.【解答】解:(1)(mx﹣3)(﹣x+n)
=﹣mx2+mnx+3x﹣3n
=﹣mx2+(mn+3)x﹣3n,
∵(mx﹣3)(﹣x+n)的展开式中不含x项,且常数项是﹣3,
∴mn+3=0,﹣3n=﹣3,
解得:m=﹣3,n=1,
∴m3+n3
=(﹣3)3+13
=﹣27+1
=﹣26;
(2)由(1)可知m=﹣3,n=1,
∴(m+n)(m2﹣mn+n2)
=m3﹣m2n+mn2+m2n﹣mn2+n3
=m3+n3
=(﹣3)3+13
=﹣27+1
=﹣26.
19.【解答】解:(1)∵5a=2,
∴53a=(5a)3=23=8;
(2)∵5b=6,5c=48,
∴5c﹣2b=5c÷52b=5c÷(5b)2=48÷62;
(3)∵(5a)3=23=8,
又∵8×6=48,
∴(5a)3×5b=5c,
即53a×5b=5c,
∴3a+b=c.
故答案为:3a+b=c.
20.【解答】解:(1)由题意可得∠AED′=130°,
∴∠DED′=180°﹣∠AED′=50°,
由折叠性质可得:,
∴∠DEF=∠EFB=25°,
故答案为:25;
(2)设ED′与BC相交于点G,
∵∠AED′=x°,
∴∠DED′=180°﹣∠AED′=(180﹣x)°,
由折叠得:,
由条件可知,∠AED′=∠EGF=x°,
∴∠EGF=∠GFC′=x°,
由条件可知:∠GFC″=∠GFC′=x°,
∴,
故答案为:.
21.【解答】解:(1)用含有a,b的式子表示绿化部分的总面积=(3a+b)(2a+b)﹣2(a﹣b)2
=6a2+5ab+b2﹣2(a2﹣2ab+b2)
=6a2+5ab+b2﹣2a2+4ab﹣2b2
=(4a2+9ab﹣b2)平方米.
答:用含有a,b的式子表示绿化部分的总面积为(4a2+9ab﹣b2)平方米.
(2)当a=40,b=20时,
4a2+9ab﹣b2=4×402+9×40×20﹣202=13200(平方米).
答:绿化部分的总面积为13200平方米.
22.【解答】解:(1)由题意知,盒子中篮球的个数为5(3+5)=7(个);
(2)由题意知,盒子中红球个数为3,黄球个数为5,篮球个数为7,红球的个数最少,
所以从中任意摸出一个球,摸出红球的概率最小,
故答案为:红;
(3)∵任意摸出一个球是红球的概率为,
∴此时盒子中球的总个数为312(个),
则需要减少篮球3个.
23.【解答】解:(1)∵S1=S3=mn,S2=n2,S4=m2,AD=AB=m+n,
∴(m+n)2=mn+n2+mn+m2=m2+2mn+n2,
故答案为:(m+n)2=m2+2mn+n2;
(2)若S1=3,S2=9,则mn=3,n2=9,
∴n=3,m=1,
∴m+n=1+3=4;
若m+n=12,S1=35,
∴m+n=12,mn=35,
∴m=5,n=7,
∴S2=72=49,S4=52=25,
∴S2+S4=49+25=74;
故答案为:4;74;
(3)∵△FGN与△AEN的面积之差为18,
∴S△FGN﹣S△AEN=18,
∴(S△FGN+S梯形BENF)﹣(S△AEN+S梯形BENF)=18,
即S梯形BEGF﹣S△ABF=18,
∴m(2m+n)m(m+n)=18,
∴m[(2m+n)﹣(m+n)]=18,
∴m2=36,
∴m=6或m=﹣6(负值舍去),
故m的值为6.
24.【解答】解:(1)解:,理由如下:
如图所示,过点作
∴
∵
∴
∴
∴;
(2)解:如图所示,过点作,
设,
∵
∴
设
∵,
∴,
∴,
∴
∵
∴
由(1)可得
∵
∴
∴
∴;
(3)解:∵,
∴,
设,
∵与的角平分线交于点,
设
如图所示,
由(1)可得,
∴
综上所述,
25.【解答】解:(1)不是
它们不是“和谐多项式群”.
(2)①
,,为“和谐多项式群”
②,,为“和谐多项式群”,“和谐值”为
(3)①当时
,
,(舍)
②当时
,
解得
.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年七年级下学期数学期末考试押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.深圳作为科技创新之城,有很多知名品牌,以下深圳品牌标志,其中是轴对称图形的是( )
A. B. C. D.
2.“一夜秋风起,天地桂花香.”桂花是仙游县的县花,其花粉的直径约为米,将数据用科学记数法表示为( )
A. B. C. D.
3.下列事件中,是必然事件的为( )
A.天内下雨 B.打开电视机,正在播放广告
C.人中至少有人的生日相同 D.抛掷硬币,正面向上
4.全家观影已成为过年新民俗.据悉2025年春节档共有四部重磅影片上映,分别是《射雕英雄传:侠之大者》、《封神第二部:战火西岐》、《哪吒之魔童闹海》、《:重启未来》.若小明从这四部影片中随机选择一部影片观看,则选中《哪吒之魔童闹海》的概率是( )
A. B. C. D.
5.若,则m与n之间的关系为( )
A. B. C. D.
6.下列长度的三条线段,能组成三角形的是( )
A.4,4,5 B.1,3,4 C.5,6,12 D.1,6,8
7.不论为何值,等式都成立,则代数式的值为( )
A. B. C.6 D.4
8.如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠DCE D.∠D+∠1+∠3=180°
9.已知x满足(x﹣2020)(x﹣2024)=516,则(x﹣2022)2的值是( )
A.512 B.516 C.520 D.1032
10.定义,以下说法正确的有( )个.
①若不含x的二次项,则.
②若为正整数,、、为自然数,,则满足条件的整式共计有9种.
③若(i为自然数),,,则.
④若,,则.
A.0 B.1 C.2 D.3
二、填空题(每小题3分,满分18分)
11.若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .
12.如图,在△ABC中,AD平分∠BAC,DE=1,则S△ACD= .
13.二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨)(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),则抽到的节气在夏季的概率为 .
14.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置点A、B分别落在直线m、n上.若∠1=70°,则∠2的度数为 .
15.如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=60°,∠C=40°,则∠DAE= 度.
16.如图,在△ABC中,∠ACB=90°,∠A=26°,点D是AC边上一动点,将△ABD沿直线BD翻折,使点A落在点F处,连接BF,交AC于点E,当△DEF是直角三角形时,则∠BDC的度数为 .
北师大版2024—2025学年七年级下学期数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:[(2x﹣y)2﹣y(2x+y)]÷2x,其中x=2,y=﹣1.
18.已知(mx﹣3)(﹣x+n)的展开式中不含x项,且常数项是﹣3.求下列各式的值:
(1)m3+n3;
(2)(m+n)(m2﹣mn+n2).
19.已知5a=2,5b=6,5c=48.
(1)求53a的值;
(2)求5c﹣2b的值;
(3)求出字母a、b、c之间的数量关系 .
20.如图1,将一条长方形纸带沿EF折叠,设∠AED'=x度.
(1)若x=130,则∠EFB= 度;
(2)将图1纸带继续沿BF折叠成图2,则∠EFC″= 度.(用含x的代数式表示)
21.如图,和谐广场有一块长为(3a+b)米,宽为(2a+b)米的长方形土地,现要将阴影部分进行绿化,在上方两角处留两块边长为(a﹣b)米的小正方形空地.
(1)用含有a,b的式子表示绿化部分的总面积;(结果写成最简形式)
(2)若a=40,b=20,求出绿化部分的总面积.
22.在一个不透明的盒子里装有除颜色外完全相同的红、黄、蓝三种颜色的球,其中红球3个,黄球5个,蓝球若干个.若从中任意摸出一个黄球的概率是.
(1)求盒子中蓝球的个数;
(2)从中任意摸出一个球,摸出 球的概率最小;
(3)能否通过只改变盒子中蓝球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整蓝球数量.
23.如图1,有边长分别为m,n的两个正方形和两个长宽分别为n,m的长方形,将它们拼成如图2所示的大正方形ABCD.四边形AHOE,HDGO,OGCF,EOFB的面积分别为S1,S2,S3,S4.
(1)用两种方法表示图2的面积,可以得到一个关于m,n的等式为 ;
(2)在图2中,若S1=3,S2=9,则m+n= ;若m+n=12,S1=35,则S2+S4= ;
(3)如图3,连接AF交EO于点N,连接GF.若△FGN与△AEN的面积之差为18,求m的值.
24.如图,已知,直线交,于,.
(1)如图1,点在直线与直线之间,请找出之间的关系,并说明理由;
(2)如图2,点在直线上,位于点右侧,点在直线上,且在直线上方,点在直线与直线之间,,,若,求.
(3)如图3,,点在直线上(在点左侧),点在直线与直线之间如图所示位置时,与的角平分线交于点,请直接写出与的数量关系.
25.定义:若多项式,,满足(其中,,是常数,且),则称多项式,,为“和谐多项式群”,常数叫做多项式,,的“和谐值”.例如多项式,,满足,那么多项式,,叫做“和谐多项式群”,常数1叫做多项式,,的“和谐值”.
(1)试判定多项式,,是否是“和谐多项式群”?若是,求出“和谐值”;若不是,请说明理由;
(2)若多项式,,为“和谐多项式群”(其中,,是常数,且),“和谐值”为.
①试说明,,满足的数量关系;
②设,试说明:;
(3),,为“和谐多项式群”,,满足且(,为常数),“和谐值”为,求出所有符合条件的,的值.
参考答案
一、选择题
1—10:ABCBD ABBCA
二、填空题
11.【解答】解:①5是腰长时,三角形的三边分别为5、3,2,
能组成三角形,
周长=5+6+2=12,
②5是底边时,三角形的三边分别为7、2、5,
不能组成三角形,
故答案为:12.
12.【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,
∴DE=DF=1,
∵AC=2,
∴S△ACD=AC DF
=×2×1
=8,
故答案为:1.
13.【解答】解:从二十四个节气中选一个节气,则抽到的节气在夏季的概率为=,
故答案为:.
14.【解答】解:如图:
∵m∥n,
∴∠ABD=∠1=70°,
∴∠2=70°﹣30°=40°.
故答案为:40°.
15.【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
又∵AE平分∠BAC,
∴∠BAE∠BAC80°=40°.
∵AD是BC上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10.
16.【解答】解:由翻折得∠F=∠A=26°,∠ABD=∠EBD,
当△DEF为直角三角形,且∠EDF=90°时,如图1,
∴∠DEF=90°﹣∠F=90°﹣26°=64°,
∴∠ABE=∠DEF﹣∠F=64°﹣26°=38°,
∴,
∴∠BDC=∠ABD+∠A=19°+26°=45°;
当△DEF为直角三角形,且∠DEF=90° 时,如图2,此时点E与点C重合,
∴∠DEB=90°,且BE,CF共线,
∵∠ABE=90°﹣∠A=90°﹣26°=64°
∴,
∴∠BDC=90°﹣∠DBE=90°﹣32°=58°,
综上所述:∠BCD的度数为45°或58°,
故答案为:45°或58°.
三、解答题
17.【解答】解:原式=(4x2﹣4xy+y2﹣2xy﹣y2)÷2x
=(4x2﹣6xy)÷2x
=2x﹣3y.
当x=2,y=﹣1时,原式=2×2﹣3×(﹣1)=7.
18.【解答】解:(1)(mx﹣3)(﹣x+n)
=﹣mx2+mnx+3x﹣3n
=﹣mx2+(mn+3)x﹣3n,
∵(mx﹣3)(﹣x+n)的展开式中不含x项,且常数项是﹣3,
∴mn+3=0,﹣3n=﹣3,
解得:m=﹣3,n=1,
∴m3+n3
=(﹣3)3+13
=﹣27+1
=﹣26;
(2)由(1)可知m=﹣3,n=1,
∴(m+n)(m2﹣mn+n2)
=m3﹣m2n+mn2+m2n﹣mn2+n3
=m3+n3
=(﹣3)3+13
=﹣27+1
=﹣26.
19.【解答】解:(1)∵5a=2,
∴53a=(5a)3=23=8;
(2)∵5b=6,5c=48,
∴5c﹣2b=5c÷52b=5c÷(5b)2=48÷62;
(3)∵(5a)3=23=8,
又∵8×6=48,
∴(5a)3×5b=5c,
即53a×5b=5c,
∴3a+b=c.
故答案为:3a+b=c.
20.【解答】解:(1)由题意可得∠AED′=130°,
∴∠DED′=180°﹣∠AED′=50°,
由折叠性质可得:,
∴∠DEF=∠EFB=25°,
故答案为:25;
(2)设ED′与BC相交于点G,
∵∠AED′=x°,
∴∠DED′=180°﹣∠AED′=(180﹣x)°,
由折叠得:,
由条件可知,∠AED′=∠EGF=x°,
∴∠EGF=∠GFC′=x°,
由条件可知:∠GFC″=∠GFC′=x°,
∴,
故答案为:.
21.【解答】解:(1)用含有a,b的式子表示绿化部分的总面积=(3a+b)(2a+b)﹣2(a﹣b)2
=6a2+5ab+b2﹣2(a2﹣2ab+b2)
=6a2+5ab+b2﹣2a2+4ab﹣2b2
=(4a2+9ab﹣b2)平方米.
答:用含有a,b的式子表示绿化部分的总面积为(4a2+9ab﹣b2)平方米.
(2)当a=40,b=20时,
4a2+9ab﹣b2=4×402+9×40×20﹣202=13200(平方米).
答:绿化部分的总面积为13200平方米.
22.【解答】解:(1)由题意知,盒子中篮球的个数为5(3+5)=7(个);
(2)由题意知,盒子中红球个数为3,黄球个数为5,篮球个数为7,红球的个数最少,
所以从中任意摸出一个球,摸出红球的概率最小,
故答案为:红;
(3)∵任意摸出一个球是红球的概率为,
∴此时盒子中球的总个数为312(个),
则需要减少篮球3个.
23.【解答】解:(1)∵S1=S3=mn,S2=n2,S4=m2,AD=AB=m+n,
∴(m+n)2=mn+n2+mn+m2=m2+2mn+n2,
故答案为:(m+n)2=m2+2mn+n2;
(2)若S1=3,S2=9,则mn=3,n2=9,
∴n=3,m=1,
∴m+n=1+3=4;
若m+n=12,S1=35,
∴m+n=12,mn=35,
∴m=5,n=7,
∴S2=72=49,S4=52=25,
∴S2+S4=49+25=74;
故答案为:4;74;
(3)∵△FGN与△AEN的面积之差为18,
∴S△FGN﹣S△AEN=18,
∴(S△FGN+S梯形BENF)﹣(S△AEN+S梯形BENF)=18,
即S梯形BEGF﹣S△ABF=18,
∴m(2m+n)m(m+n)=18,
∴m[(2m+n)﹣(m+n)]=18,
∴m2=36,
∴m=6或m=﹣6(负值舍去),
故m的值为6.
24.【解答】解:(1)解:,理由如下:
如图所示,过点作
∴
∵
∴
∴
∴;
(2)解:如图所示,过点作,
设,
∵
∴
设
∵,
∴,
∴,
∴
∵
∴
由(1)可得
∵
∴
∴
∴;
(3)解:∵,
∴,
设,
∵与的角平分线交于点,
设
如图所示,
由(1)可得,
∴
综上所述,
25.【解答】解:(1)不是
它们不是“和谐多项式群”.
(2)①
,,为“和谐多项式群”
②,,为“和谐多项式群”,“和谐值”为
(3)①当时
,
,(舍)
②当时
,
解得
.
21世纪教育网(www.21cnjy.com)
同课章节目录
