北师大版2024—2025学年八年级下学期数学期末复习调研检测卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年八年级下学期数学期末复习调研检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 681.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年八年级下学期数学期末复习调研检测卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若a>b﹣1,则下列结论一定正确的是( )
A.a+1<b B.a﹣1<b C.a>b D.a+1>b
2.下列各式中,能用完全平方公式进行因式分解的是( )
A.x2+2x﹣1 B.
C.x2+2x+4 D.x2﹣6x+9
3.剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.为了激发学生学习数学的积极性,某校举行了主题为“学数学、用数学、爱数学”的知识竞赛活动,共20道题,答对一题得5分,答错或不答扣2分,大赛规定总分不低于80分获奖,亮亮想获奖,至少答对( )道题.
A.15 B.16 C.17 D.18
5.某项工程,若甲工程队单独做可提前3天完成,若乙工程队单独做要需要甲工程队的两倍时间才能完成,现该工程先由甲乙两工程队合做5天,余下的由乙工程队独做,正好如期完成,若设工程期限为x天,则下面所列方程正确的是( )
A. B. C. D.
6.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
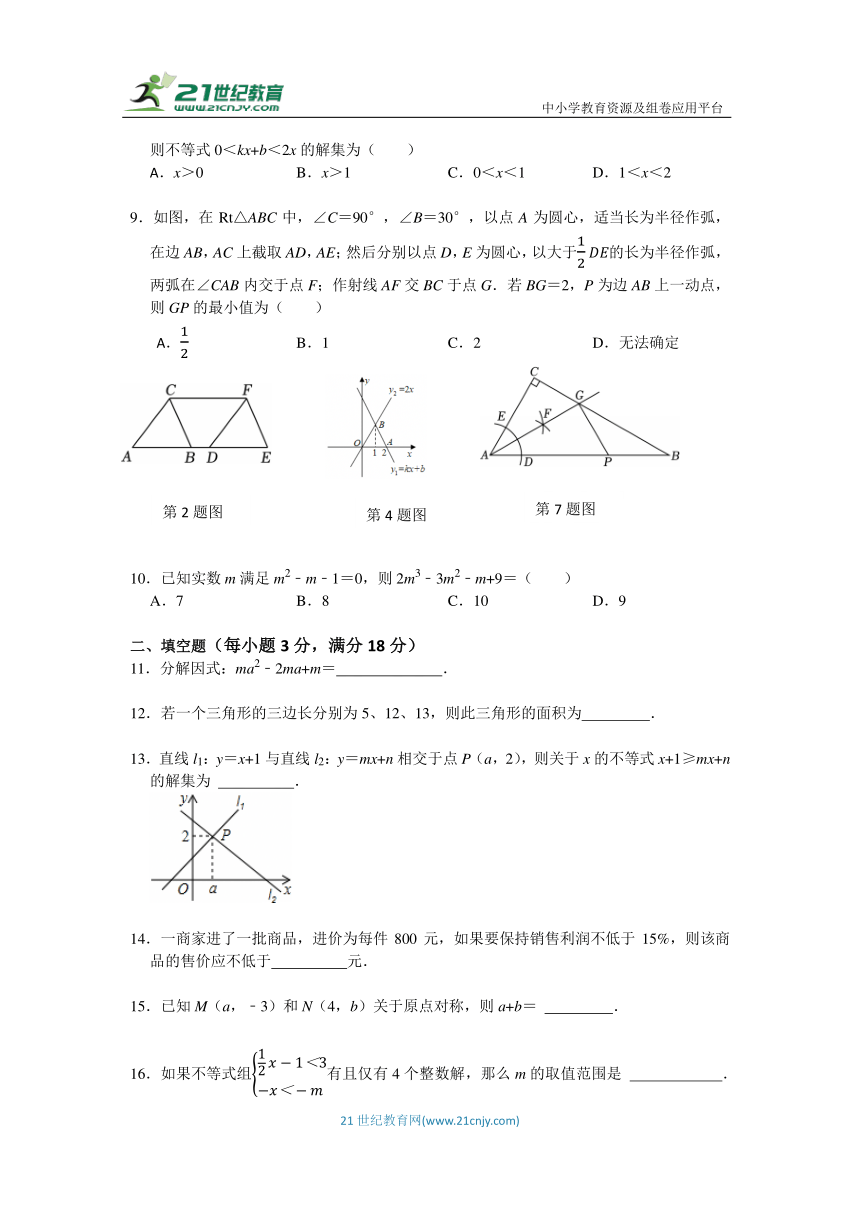
7.如图,将△ABC沿AB所在直线的方向平移至△DEF,若AE长11厘米,BD长1厘米,则平移的距离是( )
A.10厘米 B.6厘米 C.5厘米 D.4厘米
8.如图,一次函数y1=kx+b图象经过点A(2,0),与正比例函数y2=2x的图象交于点B,则不等式0<kx+b<2x的解集为( )
x>0 B.x>1 C.0<x<1 D.1<x<2
9.如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径作弧,在边AB,AC上截取AD,AE;然后分别以点D,E为圆心,以大于的长为半径作弧,两弧在∠CAB内交于点F;作射线AF交BC于点G.若BG=2,P为边AB上一动点,则GP的最小值为( )
B.1 C.2 D.无法确定
10.已知实数m满足m2﹣m﹣1=0,则2m3﹣3m2﹣m+9=( )
A.7 B.8 C.10 D.9
二、填空题(每小题3分,满分18分)
11.分解因式:ma2﹣2ma+m= .
12.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
13.直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
14.一商家进了一批商品,进价为每件800元,如果要保持销售利润不低于15%,则该商品的售价应不低于 元.
15.已知M(a,﹣3)和N(4,b)关于原点对称,则a+b= .
16.如果不等式组有且仅有4个整数解,那么m的取值范围是 .
北师大版2024—2025学年八年级下学期数学期末复习调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列不等式或不等式组,并将解集在数轴上表示出来.
(1)3x<5(x+2);(2).
18.如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
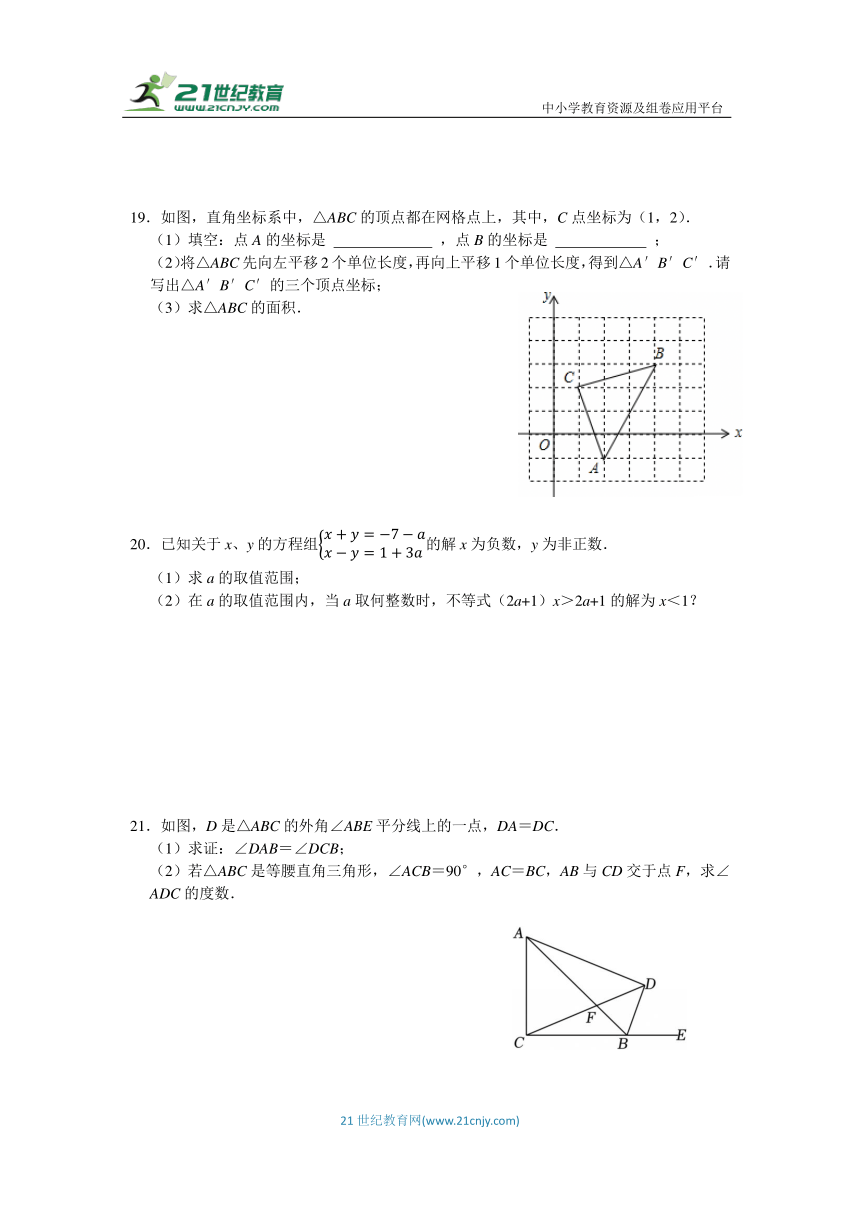
19.如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3)求△ABC的面积.
20.已知关于x、y的方程组的解x为负数,y为非正数.
(1)求a的取值范围;
(2)在a的取值范围内,当a取何整数时,不等式(2a+1)x>2a+1的解为x<1?
21.如图,D是△ABC的外角∠ABE平分线上的一点,DA=DC.
(1)求证:∠DAB=∠DCB;
(2)若△ABC是等腰直角三角形,∠ACB=90°,AC=BC,AB与CD交于点F,求∠ADC的度数.
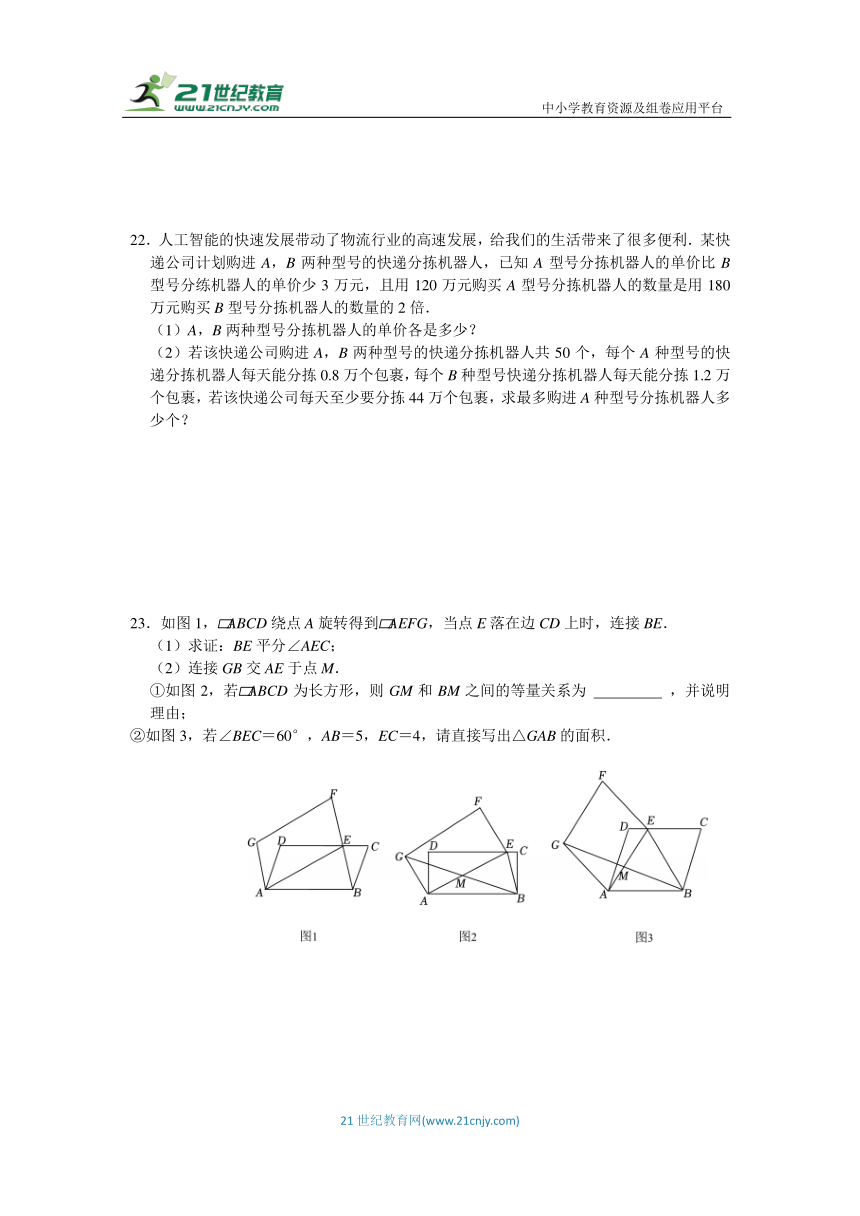
22.人工智能的快速发展带动了物流行业的高速发展,给我们的生活带来了很多便利.某快递公司计划购进A,B两种型号的快递分拣机器人,已知A型号分拣机器人的单价比B型号分练机器人的单价少3万元,且用120万元购买A型号分拣机器人的数量是用180万元购买B型号分拣机器人的数量的2倍.
(1)A,B两种型号分拣机器人的单价各是多少?
(2)若该快递公司购进A,B两种型号的快递分拣机器人共50个,每个A种型号的快递分拣机器人每天能分拣0.8万个包裹,每个B种型号快递分拣机器人每天能分拣1.2万个包裹,若该快递公司每天至少要分拣44万个包裹,求最多购进A种型号分拣机器人多少个?
23.如图1, ABCD绕点A旋转得到 AEFG,当点E落在边CD上时,连接BE.
(1)求证:BE平分∠AEC;
(2)连接GB交AE于点M.
①如图2,若 ABCD为长方形,则GM和BM之间的等量关系为 ,并说明理由;
②如图3,若∠BEC=60°,AB=5,EC=4,请直接写出△GAB的面积.
24.在平面直角坐标系xOy中,直线l1:y=﹣x+4分别与x轴,y轴相交于A,B两点,直线l2:y=kx+2k(k≠0)与x轴相交于点C,与直线l1相交于点D,连接BC.
(1)分别求点A,B,C的坐标;
(2)设△BCD的面积为S1,△ACD的面积为S2,若,求直线l2的函数表达式;
(3)以BC,CD为边作 BCDE,连接CE,交BD于点F,分别取DE的中点M,BE的中点N,连接FM,FN,当FM+FN取得最小值时,求此时 BCDE的面积.
25.给出定义:如果两个实数m,n使得关于x的分式方程的解是成立,那么我们就把实数m,n组成的数对<m,n>称为关于x的分式方程的一个“梦想数对”.
例如:当m=3,n=2时,使得关于x的分式方程的解是成立,所以数对(3,2)称为关于x的分式方程的一个“梦想数对”.
(1)在数对①<1,0>;②<﹣2,3>;③,中, (只填序号)是关于x的分式方程的“梦想数对”.
(2)若数对<a﹣3,2+a>是关于x的分式方程的一个“梦想数对”,求a的值.
(3)若数对<c+d,d>(c≠±1且c≠0)是关于x的分式方程的一个“梦想数对”,且关于y的方程dy﹣c+1=0有整数解,直接写出整数c的值.
参考答案
一、选择题
1—10:DDDDA BBDBB
二、填空题
11.【解答】解:ma2﹣2ma+m
=m(a2﹣2a+1)
=m(a﹣1)2,
故答案为:m(a﹣1)2.
12.【解答】解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为5×12=30.
13.【解答】解:将点P(a,2)坐标代入直线y=x+1,得a=1,
从图中直接看出,当x≥1时,x+1≥mx+n,
故答案为:x≥1.
14.【解答】解:设售价应x元,则(x﹣800)÷800≥15%,解得x≥920元.
15.【解答】解:∵M(a,﹣3)和N(4,b)关于原点对称,
∴a=﹣4,b=3,
则a+b=﹣4+3=﹣1.
故答案为:﹣1.
16.【解答】解:,
解不等式x﹣1<3,得x<8,
解不等式﹣x<﹣m,得x>m,
不等式组的解集是m<x<8,
∵不等式组有且仅有4个整数解,这3个整数解是4,5,6,7,
∴3≤m<4,
故答案为:3≤m<4.
三、解答题
17.【解答】解:(1)去括号得:3x<5x+10,
移项,合并同类项得:﹣2x<10,
系数化为1得:x>﹣5,
将解集表示在数轴上,如图所示:
(2),
解不等式①得:x>﹣1,
解不等式②得:x≤6,
∴不等式组的解集为:﹣1<x≤6,
如图所示:解集表示在数轴上,
18.【解答】(1)证明:由旋转得,CD=CE.
∵∠DCE=∠ACB,
∴∠DCE﹣∠DCB=∠ACB﹣∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠CBA=60°,CA=CB,
∴△ABC是等边三角形,
∴∠CAB=60°.
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
19.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1),(4,3);
(2)如图,△A′B′C′为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)△ABC的面积=3×42×43×13×1=5.
20.【解答】解:(1)解方程组得,
由题意知,
解不等式①,得:a<3,
解不等式②,得:a≥﹣2,
则不等式组的解集为﹣2≤a<3;
(2)∵不等式(2a+1)x>2a+1的解为x<1,
∴2a+1<0,
解得a<﹣0.5,
又﹣2≤a<3且a为整数,
所以a=﹣2或﹣1.
21.【解答】(1)证明:如下图,过点D作DG⊥AB于点G,作DH⊥BE于点H,
∴∠DGA=∠DHC=90°,
∵BD平分∠ABE,DG⊥AB,DH⊥BE,
∴DG=DH,
在Rt△DGA和Rt△DHC中,
,
∴Rt△DGA≌Rt△DHC(HL),
∴∠DAB=∠DCB;
(2)证明:∵DA=DC,
∴∠DCA=∠DAC=∠BAC+∠BAD,
∵∠ACB=90°,AC=BC,
∴,
∴∠ABE=180°﹣∠ABC=135°,
又∵BD平分∠ABE,
∴,
∴∠BDG=∠BDH=90°﹣67.5°=22.5°,
∴∠GDH=∠BDG+∠BDH=45°,
由(1)可知,Rt△DGA≌Rt△DHC,
∴∠ADG=∠CDH,即∠ADF+∠FDG=∠FDG+∠GDH,
∴∠ADF=∠GDH=45°,
∴∠ADF=∠BAC=45°.
22.【解答】解:(1)设A型号分拣机器人的单价是x万元,则B型号分拣机器人的单价是(x+3)万元,
根据题意得:2,
解得:x=1.5,
经检验,x=1.5是所列方程的解,且符合题意,
∴x+3=1.5+3=4.5.
答:A型号分拣机器人的单价是1.5万元,B型号分拣机器人的单价是4.5万元;
(2)设购进A种型号分拣机器人m个,则购进B种型号分拣机器人(50﹣m)个,
根据题意得:0.8m+1.2(50﹣m)≥44,
解得:m≤40,
∴m的最大值为40.
答:最多购进A种型号分拣机器人40个.
23.【解答】(1)证明:∵AB∥CD,
则∠EBA=∠BEC,
∵AB=AE,则∠ABE=∠AEB=CEB,
即BE平分∠AEC;
(2)解:①过点B作BT⊥AE于点T,
由(1)知,BE平分∠AEC,
则BT=BC=AG,
∵∠GAM=∠BTM=90°,∠AMG=∠BMT,
∴△AMG≌△TMB(AAS),
∴MG=MB,
故答案为:相等;
②作射线DL,
∵∠BEC=60°,AB=AE,
则△ABE为等边三角形,则∠EAB=∠AEB=∠EBA=60°=∠CEB,AE=BE,
故∠DEN=60°=∠AEB,
在AE上取EN=ED,连接BN、GN,
则△ADE≌△BNE(SAS),
∴BN=AD=AG,∠ADE=∠BNE,
则∠ANB=∠LDA,
∵AB∥CD,则∠LDA=∠DAB
由图形的旋转知,∠DAB=∠GAE,
则∠GAE=∠BAN,
∵∠GMA=∠BMN,BN=AG,
∴△AMG≌△NMB(AAS),
则∠AGB=∠NBM,
则GA∥BN,
则四边形ABNC为平行四边形,
则△GAB的面积=△NAB的面积,
∵AB=5,EC=4,则DE=1=EN,
过点N作NT⊥AB于点T,
在Rt△ANT中,∠NAB=60°,AN=AE﹣EN=5﹣1=4,
则NT2,
则△GAB的面积=△NAB的面积AB×NT5×25.
24.【解答】解:(1)对于直线l:y=﹣x+4,
当x=0时,y=4,
当y=0时,﹣x+4=0,
解得x=4,
∴A(4,0),B(0,4),
对于直线 l2:y=kx+2k(k≠0),
当y=0时,kx+2k=0,
解得:x=﹣2,
∴C(﹣2,0),
故A(4,0),B(0,4),C(﹣2,0);
(2)∵,
∴S1>S2
①当点D在线段BA上时,
AC=4﹣(﹣2)=6,OB=4,
∴12,
∴S2AC×yD=3yD,
∴S1=S△ABC﹣S2=12﹣3yD,
∵,
∴,
解得yD=1,
经检验:yD=1是方程的解,
∴﹣x+4=1,
解得x=3,
∴D(3,1),
∴3k+2k=1,
解得,
∴直线l2的函数表达式为:;
②当点D在线段BA的延长线上时,
3yD,
∴S1=S△ABC+S2=12﹣3yD,
∵,
∴3,
解得yD=﹣2,
经检验yD=﹣2是方程的解,
∴﹣x+4=﹣2,
解得x=6,
∴D(6,﹣2),
∴6k+2k=﹣2,
解得,
∴直线l2的函数表达式为:;
综上所述:直线l2的函数表达式为:或;
(3)如图,作DH⊥x轴交于H,
由(1)得,
∵四边形BCDE是平行四边形,
∴CF=EF,
∵N是BE的中点,M是DE的中点,
∴,,
∴FM+FN,
∴CD取最小值时,FM+FN取得最小值,当CD⊥AB时,CD取最小值,
∵OA=OB=4,
∴∠OAB=45°,
∴,
∴∠ACD=∠CAD=45°,
∴CD=AD,
∴,
∴AH=DH=3,
∴,,
∴BD,
∴6;
∴S BCDE=2S△BDC=6;
故 BCDE的面积为6.
25.【解答】解:(1)当m=1,n=0时,使得关于x的分式方程的解是1成立,所以数对(1,0)是关于x的分式方程的一个“梦想数对”,故①正确;
当m=﹣2,n=3时,使得关于x的分式方程1的解是,不是成立,所以数对(﹣2,3)不是关于x的分式方程的一个“梦想数对”,故②错误;
当,时,使得关于x的分式方程的解是x成立,所以数对是关于x的分式方程的一个“梦想数对”,故③正确;
故答案为:①③;
(2)根据定义,分式方程1的解为,
故,
解得a=2;
(3)根据数对(c+d,d)(c≠±1且c≠0)是关于x的分式方程的一个“梦想数对”,得关于x的分式方程的解是,回代方程,得c2+cd﹣d=1,
整理,得(c﹣1)(c+1)+d(c﹣1)=0,
∴(c﹣1)(c+d+1)=0,
∵c≠±1且c≠0,
∴c+d+1=0,
∴c=﹣d﹣1,
∵方程dy﹣c+1=0的解为y,
∴,
∵方程有整数解,
∴d=±1,d=±2,
当d=±1时,c=﹣2,c=0(舍去);
当d=±2时,c=﹣3,c=1(舍去);
故c=﹣2或c=﹣3.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年八年级下学期数学期末复习调研检测卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若a>b﹣1,则下列结论一定正确的是( )
A.a+1<b B.a﹣1<b C.a>b D.a+1>b
2.下列各式中,能用完全平方公式进行因式分解的是( )
A.x2+2x﹣1 B.
C.x2+2x+4 D.x2﹣6x+9
3.剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.为了激发学生学习数学的积极性,某校举行了主题为“学数学、用数学、爱数学”的知识竞赛活动,共20道题,答对一题得5分,答错或不答扣2分,大赛规定总分不低于80分获奖,亮亮想获奖,至少答对( )道题.
A.15 B.16 C.17 D.18
5.某项工程,若甲工程队单独做可提前3天完成,若乙工程队单独做要需要甲工程队的两倍时间才能完成,现该工程先由甲乙两工程队合做5天,余下的由乙工程队独做,正好如期完成,若设工程期限为x天,则下面所列方程正确的是( )
A. B. C. D.
6.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
7.如图,将△ABC沿AB所在直线的方向平移至△DEF,若AE长11厘米,BD长1厘米,则平移的距离是( )
A.10厘米 B.6厘米 C.5厘米 D.4厘米
8.如图,一次函数y1=kx+b图象经过点A(2,0),与正比例函数y2=2x的图象交于点B,则不等式0<kx+b<2x的解集为( )
x>0 B.x>1 C.0<x<1 D.1<x<2
9.如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径作弧,在边AB,AC上截取AD,AE;然后分别以点D,E为圆心,以大于的长为半径作弧,两弧在∠CAB内交于点F;作射线AF交BC于点G.若BG=2,P为边AB上一动点,则GP的最小值为( )
B.1 C.2 D.无法确定
10.已知实数m满足m2﹣m﹣1=0,则2m3﹣3m2﹣m+9=( )
A.7 B.8 C.10 D.9
二、填空题(每小题3分,满分18分)
11.分解因式:ma2﹣2ma+m= .
12.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
13.直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
14.一商家进了一批商品,进价为每件800元,如果要保持销售利润不低于15%,则该商品的售价应不低于 元.
15.已知M(a,﹣3)和N(4,b)关于原点对称,则a+b= .
16.如果不等式组有且仅有4个整数解,那么m的取值范围是 .
北师大版2024—2025学年八年级下学期数学期末复习调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列不等式或不等式组,并将解集在数轴上表示出来.
(1)3x<5(x+2);(2).
18.如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
19.如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3)求△ABC的面积.
20.已知关于x、y的方程组的解x为负数,y为非正数.
(1)求a的取值范围;
(2)在a的取值范围内,当a取何整数时,不等式(2a+1)x>2a+1的解为x<1?
21.如图,D是△ABC的外角∠ABE平分线上的一点,DA=DC.
(1)求证:∠DAB=∠DCB;
(2)若△ABC是等腰直角三角形,∠ACB=90°,AC=BC,AB与CD交于点F,求∠ADC的度数.
22.人工智能的快速发展带动了物流行业的高速发展,给我们的生活带来了很多便利.某快递公司计划购进A,B两种型号的快递分拣机器人,已知A型号分拣机器人的单价比B型号分练机器人的单价少3万元,且用120万元购买A型号分拣机器人的数量是用180万元购买B型号分拣机器人的数量的2倍.
(1)A,B两种型号分拣机器人的单价各是多少?
(2)若该快递公司购进A,B两种型号的快递分拣机器人共50个,每个A种型号的快递分拣机器人每天能分拣0.8万个包裹,每个B种型号快递分拣机器人每天能分拣1.2万个包裹,若该快递公司每天至少要分拣44万个包裹,求最多购进A种型号分拣机器人多少个?
23.如图1, ABCD绕点A旋转得到 AEFG,当点E落在边CD上时,连接BE.
(1)求证:BE平分∠AEC;
(2)连接GB交AE于点M.
①如图2,若 ABCD为长方形,则GM和BM之间的等量关系为 ,并说明理由;
②如图3,若∠BEC=60°,AB=5,EC=4,请直接写出△GAB的面积.
24.在平面直角坐标系xOy中,直线l1:y=﹣x+4分别与x轴,y轴相交于A,B两点,直线l2:y=kx+2k(k≠0)与x轴相交于点C,与直线l1相交于点D,连接BC.
(1)分别求点A,B,C的坐标;
(2)设△BCD的面积为S1,△ACD的面积为S2,若,求直线l2的函数表达式;
(3)以BC,CD为边作 BCDE,连接CE,交BD于点F,分别取DE的中点M,BE的中点N,连接FM,FN,当FM+FN取得最小值时,求此时 BCDE的面积.
25.给出定义:如果两个实数m,n使得关于x的分式方程的解是成立,那么我们就把实数m,n组成的数对<m,n>称为关于x的分式方程的一个“梦想数对”.
例如:当m=3,n=2时,使得关于x的分式方程的解是成立,所以数对(3,2)称为关于x的分式方程的一个“梦想数对”.
(1)在数对①<1,0>;②<﹣2,3>;③,中, (只填序号)是关于x的分式方程的“梦想数对”.
(2)若数对<a﹣3,2+a>是关于x的分式方程的一个“梦想数对”,求a的值.
(3)若数对<c+d,d>(c≠±1且c≠0)是关于x的分式方程的一个“梦想数对”,且关于y的方程dy﹣c+1=0有整数解,直接写出整数c的值.
参考答案
一、选择题
1—10:DDDDA BBDBB
二、填空题
11.【解答】解:ma2﹣2ma+m
=m(a2﹣2a+1)
=m(a﹣1)2,
故答案为:m(a﹣1)2.
12.【解答】解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为5×12=30.
13.【解答】解:将点P(a,2)坐标代入直线y=x+1,得a=1,
从图中直接看出,当x≥1时,x+1≥mx+n,
故答案为:x≥1.
14.【解答】解:设售价应x元,则(x﹣800)÷800≥15%,解得x≥920元.
15.【解答】解:∵M(a,﹣3)和N(4,b)关于原点对称,
∴a=﹣4,b=3,
则a+b=﹣4+3=﹣1.
故答案为:﹣1.
16.【解答】解:,
解不等式x﹣1<3,得x<8,
解不等式﹣x<﹣m,得x>m,
不等式组的解集是m<x<8,
∵不等式组有且仅有4个整数解,这3个整数解是4,5,6,7,
∴3≤m<4,
故答案为:3≤m<4.
三、解答题
17.【解答】解:(1)去括号得:3x<5x+10,
移项,合并同类项得:﹣2x<10,
系数化为1得:x>﹣5,
将解集表示在数轴上,如图所示:
(2),
解不等式①得:x>﹣1,
解不等式②得:x≤6,
∴不等式组的解集为:﹣1<x≤6,
如图所示:解集表示在数轴上,
18.【解答】(1)证明:由旋转得,CD=CE.
∵∠DCE=∠ACB,
∴∠DCE﹣∠DCB=∠ACB﹣∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠CBA=60°,CA=CB,
∴△ABC是等边三角形,
∴∠CAB=60°.
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
19.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1),(4,3);
(2)如图,△A′B′C′为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)△ABC的面积=3×42×43×13×1=5.
20.【解答】解:(1)解方程组得,
由题意知,
解不等式①,得:a<3,
解不等式②,得:a≥﹣2,
则不等式组的解集为﹣2≤a<3;
(2)∵不等式(2a+1)x>2a+1的解为x<1,
∴2a+1<0,
解得a<﹣0.5,
又﹣2≤a<3且a为整数,
所以a=﹣2或﹣1.
21.【解答】(1)证明:如下图,过点D作DG⊥AB于点G,作DH⊥BE于点H,
∴∠DGA=∠DHC=90°,
∵BD平分∠ABE,DG⊥AB,DH⊥BE,
∴DG=DH,
在Rt△DGA和Rt△DHC中,
,
∴Rt△DGA≌Rt△DHC(HL),
∴∠DAB=∠DCB;
(2)证明:∵DA=DC,
∴∠DCA=∠DAC=∠BAC+∠BAD,
∵∠ACB=90°,AC=BC,
∴,
∴∠ABE=180°﹣∠ABC=135°,
又∵BD平分∠ABE,
∴,
∴∠BDG=∠BDH=90°﹣67.5°=22.5°,
∴∠GDH=∠BDG+∠BDH=45°,
由(1)可知,Rt△DGA≌Rt△DHC,
∴∠ADG=∠CDH,即∠ADF+∠FDG=∠FDG+∠GDH,
∴∠ADF=∠GDH=45°,
∴∠ADF=∠BAC=45°.
22.【解答】解:(1)设A型号分拣机器人的单价是x万元,则B型号分拣机器人的单价是(x+3)万元,
根据题意得:2,
解得:x=1.5,
经检验,x=1.5是所列方程的解,且符合题意,
∴x+3=1.5+3=4.5.
答:A型号分拣机器人的单价是1.5万元,B型号分拣机器人的单价是4.5万元;
(2)设购进A种型号分拣机器人m个,则购进B种型号分拣机器人(50﹣m)个,
根据题意得:0.8m+1.2(50﹣m)≥44,
解得:m≤40,
∴m的最大值为40.
答:最多购进A种型号分拣机器人40个.
23.【解答】(1)证明:∵AB∥CD,
则∠EBA=∠BEC,
∵AB=AE,则∠ABE=∠AEB=CEB,
即BE平分∠AEC;
(2)解:①过点B作BT⊥AE于点T,
由(1)知,BE平分∠AEC,
则BT=BC=AG,
∵∠GAM=∠BTM=90°,∠AMG=∠BMT,
∴△AMG≌△TMB(AAS),
∴MG=MB,
故答案为:相等;
②作射线DL,
∵∠BEC=60°,AB=AE,
则△ABE为等边三角形,则∠EAB=∠AEB=∠EBA=60°=∠CEB,AE=BE,
故∠DEN=60°=∠AEB,
在AE上取EN=ED,连接BN、GN,
则△ADE≌△BNE(SAS),
∴BN=AD=AG,∠ADE=∠BNE,
则∠ANB=∠LDA,
∵AB∥CD,则∠LDA=∠DAB
由图形的旋转知,∠DAB=∠GAE,
则∠GAE=∠BAN,
∵∠GMA=∠BMN,BN=AG,
∴△AMG≌△NMB(AAS),
则∠AGB=∠NBM,
则GA∥BN,
则四边形ABNC为平行四边形,
则△GAB的面积=△NAB的面积,
∵AB=5,EC=4,则DE=1=EN,
过点N作NT⊥AB于点T,
在Rt△ANT中,∠NAB=60°,AN=AE﹣EN=5﹣1=4,
则NT2,
则△GAB的面积=△NAB的面积AB×NT5×25.
24.【解答】解:(1)对于直线l:y=﹣x+4,
当x=0时,y=4,
当y=0时,﹣x+4=0,
解得x=4,
∴A(4,0),B(0,4),
对于直线 l2:y=kx+2k(k≠0),
当y=0时,kx+2k=0,
解得:x=﹣2,
∴C(﹣2,0),
故A(4,0),B(0,4),C(﹣2,0);
(2)∵,
∴S1>S2
①当点D在线段BA上时,
AC=4﹣(﹣2)=6,OB=4,
∴12,
∴S2AC×yD=3yD,
∴S1=S△ABC﹣S2=12﹣3yD,
∵,
∴,
解得yD=1,
经检验:yD=1是方程的解,
∴﹣x+4=1,
解得x=3,
∴D(3,1),
∴3k+2k=1,
解得,
∴直线l2的函数表达式为:;
②当点D在线段BA的延长线上时,
3yD,
∴S1=S△ABC+S2=12﹣3yD,
∵,
∴3,
解得yD=﹣2,
经检验yD=﹣2是方程的解,
∴﹣x+4=﹣2,
解得x=6,
∴D(6,﹣2),
∴6k+2k=﹣2,
解得,
∴直线l2的函数表达式为:;
综上所述:直线l2的函数表达式为:或;
(3)如图,作DH⊥x轴交于H,
由(1)得,
∵四边形BCDE是平行四边形,
∴CF=EF,
∵N是BE的中点,M是DE的中点,
∴,,
∴FM+FN,
∴CD取最小值时,FM+FN取得最小值,当CD⊥AB时,CD取最小值,
∵OA=OB=4,
∴∠OAB=45°,
∴,
∴∠ACD=∠CAD=45°,
∴CD=AD,
∴,
∴AH=DH=3,
∴,,
∴BD,
∴6;
∴S BCDE=2S△BDC=6;
故 BCDE的面积为6.
25.【解答】解:(1)当m=1,n=0时,使得关于x的分式方程的解是1成立,所以数对(1,0)是关于x的分式方程的一个“梦想数对”,故①正确;
当m=﹣2,n=3时,使得关于x的分式方程1的解是,不是成立,所以数对(﹣2,3)不是关于x的分式方程的一个“梦想数对”,故②错误;
当,时,使得关于x的分式方程的解是x成立,所以数对是关于x的分式方程的一个“梦想数对”,故③正确;
故答案为:①③;
(2)根据定义,分式方程1的解为,
故,
解得a=2;
(3)根据数对(c+d,d)(c≠±1且c≠0)是关于x的分式方程的一个“梦想数对”,得关于x的分式方程的解是,回代方程,得c2+cd﹣d=1,
整理,得(c﹣1)(c+1)+d(c﹣1)=0,
∴(c﹣1)(c+d+1)=0,
∵c≠±1且c≠0,
∴c+d+1=0,
∴c=﹣d﹣1,
∵方程dy﹣c+1=0的解为y,
∴,
∵方程有整数解,
∴d=±1,d=±2,
当d=±1时,c=﹣2,c=0(舍去);
当d=±2时,c=﹣3,c=1(舍去);
故c=﹣2或c=﹣3.
21世纪教育网(www.21cnjy.com)
同课章节目录
