华东师大版2024—2025学年七年级下册数学期末考试模拟试卷(含答案)
文档属性
| 名称 | 华东师大版2024—2025学年七年级下册数学期末考试模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 21:11:36 | ||
图片预览




文档简介
华东师大版2024—2025学年七年级下册数学期末考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.不等式组,的解集在数轴上表示为( )
A. B.
C. D.
3.若a>b,则下列不等式不一定成立的是( )
A.3a>3b B.a﹣1>b﹣2 C.a2>b2 D.1﹣3a<1﹣3b
4.解方程时,去分母结果正确的是( )
A. B.
C. D.
5.电影哪吒之魔童闹海的热映,推动了我国国产动画电影发展,提升了中国文化影响力,下列哪吒图片的变换顺序描述正确的是( )
A.轴对称,平移,旋转 B.旋转,轴对称,平移
C.轴对称,旋转,平移 D.平移,旋转,轴对称
6.明代大数学家程大位著的《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问君多少能完成 ”也就是说:有根短竹,每根短竹可制成毛笔的笔管个或笔套个,怎样安排制作笔管或笔套的短竹数量,使制成的笔管数量与笔套数量正好配套 下列说法正确的是( )
A.设用于制作笔管的短竹数为x根,则可列方程为
B.设用于制作笔管的短竹数为x根,则可列方程为
C.设用于制作笔套的短竹数为y根,则可列方程为
D.设用于制作笔套的短竹数为y根,则可列方程为
7.关于x的一元一次不等式中,m的值应为( )
A.0 B.1 C.2 D.0或2
8.已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
9.如图,已知长方形纸片,点,在边上,点,在边上,分别沿,折叠,使点和点都落在点处,若,则的度数为( )
A. B. C. D.
10.关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.已知方程(m﹣2)x|m|﹣1+8=0是关于x的一元一次方程,则m的值为 .
12.如果,那么x+y+z的值为 .
13.一种运算:x*y=ax+by(a,b为常数),若3*4=2,5*(﹣1)=11,则2*6= .
14.若且abc≠0,则 .
15.若关于x的不等式组仅有5个整数解,则a的取值范围为 .
16.若关于x的一元一次方程的解为x=1,则关于y的一元一次方程ay+b=2y+c的解为y= .
第II卷
华东师大版2024—2025学年七年级下册数学期末考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程组:
(1); (2).
18.(1)解不等式组: (2)解不等式组:
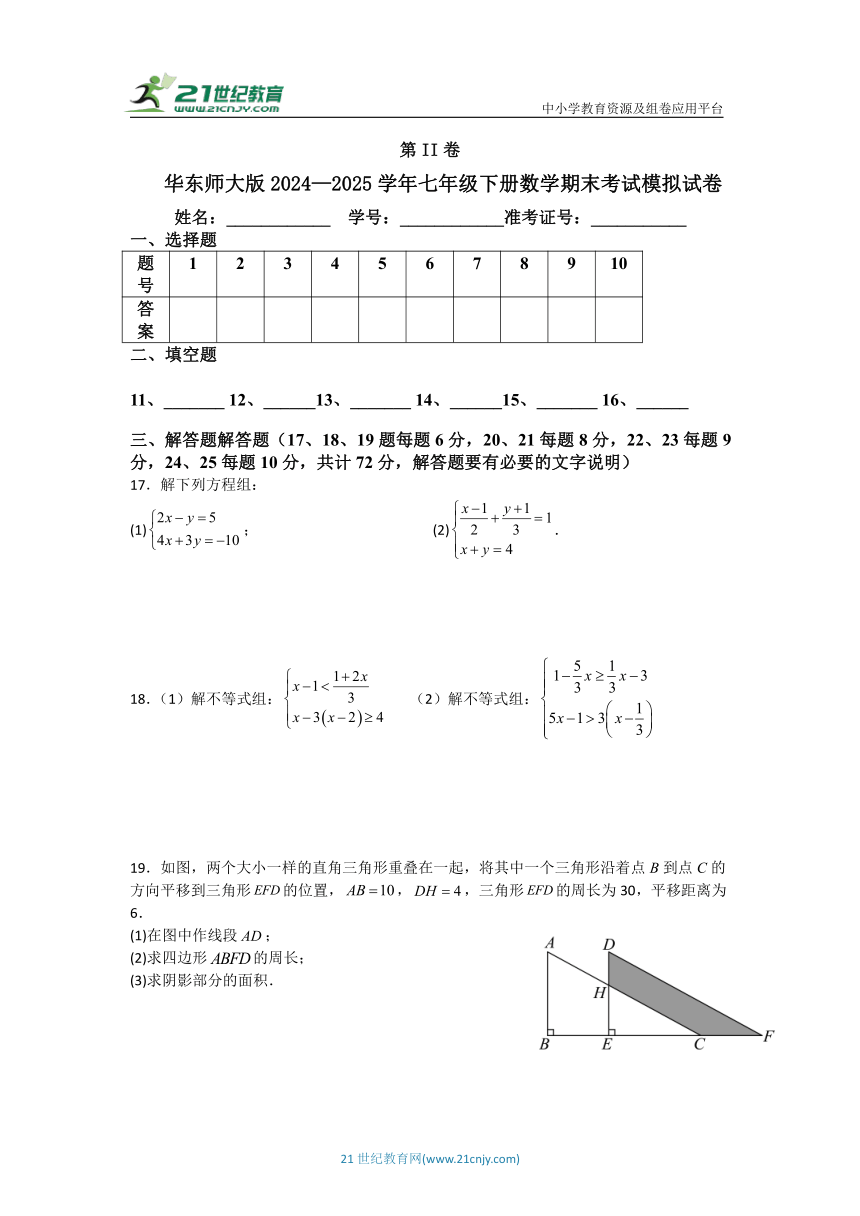
19.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形的位置,,,三角形的周长为30,平移距离为6.
(1)在图中作线段;
(2)求四边形的周长;
(3)求阴影部分的面积.
20.广西平陆运河北起横州市西津水电站库区平塘江口,南止于钦江出海口沙井港航道,在一航道建设中,某渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方.已知5辆大型渣土运输车与2辆小型渣土运输车一次共运输土方吨,6辆大型渣土运输车与4辆小型渣土运输车一次共运输土方吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨
(2)该渣土运输公司决定派出大、小两种型号渣土运输车共辆参与把吨土方全部运走,那么大型渣土运输车至少需要多少辆
21.已知关于x、y的方程满足方程组.
(1)若,求m的值;
(2)若x、y均为非负数,求m的取值范围.
22.在中,过点作交其延长线于点,作的平分线交于点,过点作交于点、交于点.
(1)求证:.
(2)连接,若平分,,求的度数.
23.【阅读】若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”.
【举例】方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“关联方程”.
【问题】
(1)方程是不是不等式组的“关联方程”?请说明理由.
(2)若关于的方程是不等式组的“关联方程”,求的取值范围;
(3)若关于的方程是关于的不等式组的“关联方程”,且此时不等式组有4个整数解,试求的取值范围.
24.已知,直线与交于点,与交于点,点,均不与点重合,平分平分.
(1)如图1,求的度数;
(2)如图2,延长与交于点,过作射线与交于点,且满足.求证:;
(3)如图3,过点作是的外角平分线所在直线,与射线交于点,与交于点.在中,如果有一个角的度数是另一个角的3倍,请直接写出的度数.
25.如图,等腰的对称轴与底边交于点,,,其中、是二元一次方程组的解,,点是边上的一个动点,过点作于点,作于点.
(1)求的面积;
(2)当点在线段上运动时,求的值;
(3)当点在线段的延长线上运动时连接,当时,请补全图形,求此时线段的长.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1—10:DBCDA BDACB
二、填空题
11.【解答】解:由题意可得:|m|﹣1=1且m﹣2≠0,
解得m=﹣2.
故答案为:﹣2.
12.【解答】解:三个方程相加可得:2x+2y+2z=18,
所以x+y+z=9,
故答案为:9
13.【解答】解:∵3*4=2,5*(﹣1)=11,
,
解得:a=2,b=﹣1,
∴2*6=2×2+6×(﹣1)=﹣2,
故答案为:﹣2.
14.【解答】解:设k,
则a=2k,b=3k,c=4k,
所以
=3.
故答案为:3.
15.【解答】解:,
解不等式①得:,
解不等式②得:x≤3,
∵不等式组有5个整数解,即:﹣1,0,1,2,3,
∴,
∴﹣6≤a<﹣3,
故答案为:﹣6≤a<﹣3.
16.【解答】解:,
,
∵关于x的一元一次方程的解为x=1,
∴关于y的一元一次方程ay+b=2y+c的解为:,
故答案为:.
三、解答题
17.(1)解:,
,得,
解得:,
将代入①,得,
解得:,
∴原方程组的解为;
(2)解:,
整理得
由②得,
把③代入①,得,
去括号,得,
解得:,
将代入②,得,
解得:,
∴原方程组的解为.
18.解:(1),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
(1),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
19.(1)解:线段如图所示;
(2)解:∵三角形的周长为30,平移距离为6,
∴,,,
∴四边形的周长
;
(3)解:∵平移得到,
∴,,,
∴,即:梯形的面积等于阴影部分的面积,
∵,
∴梯形的面积为,
∴阴影部分的面积为.
20.(1)解:设一辆大型渣土运输车一次运输土方 x 吨,一辆小型渣土运输车一次运输土方y 吨,
根据题意得 :
解得:.
答:一辆大型渣土运输车一次运输土方吨,一辆小型渣土运输车一次运输土方 5 吨;
(2)解:设需要安排 m 辆大型渣土运输车,则安排辆小型渣土运输车,
根据题意得:,
解得:.
又∵,且为正整数,
∴,
答:至少需要大型渣土车辆.
21.(1)解:,
得:,
,
解得:;
(2)解:
得:,解得,
把代入②得:,解得,
∴原方程组的解为,
、均为非负数,
,,
∴,
解得:.
22.(1)证明:∵平分,
∴,即,
∵,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:由()得:,
∵,
∴,
∴,
∵平分,
∴,
∴.
23.(1)解:方程是不是不等式组的“关联方程”.
理由:由方程,
解得:,
解不等式组,
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:,
∵在的范围内,
∴方程是不等式组的“关联方程”.
(2)解:,
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:,
由方程,
解得:.
∵关于的方程是不等式组的“关联方程”,
,解得:;
(3)解:由关于的方程,
解得:;
,
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:,
∵不等式组有4个整数解,
∴整数的值为1,2,3,4,
∴,
.
∵关于的方程是关于的不等式组的“关联方程”,
,
解得:,
∴的取值范围:.
24.(1)解:∵,平分,平分,
∴,
∴,
∴;
(2)解:∵平分,平分,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴,
∴;
(3)分情况讨论;①当时,
∵,即,
∴,
∴.
∵是的外角平分线所在的直线,
∴.
∵是的外角,
∴.
∵平分,
∴,
∴.
∵平分,
∴;
当时,
∴.
∵是的外角平分线所在的直线,
∴,
∴.
∵平分,
∴,
∴.
∵平分,
∴.
综上所述,的度数为或.
24.(1)解:解方程组
①②得
解得:,
将代入②得,
解得:
是等腰三角形,对称轴与底边交于点,
∴,
根据等腰三角形三线合一,,
则,,
根据三角形面积公式;
(2)连接,如图所示:
∵,
;
(3)画出点在延长线上,,,如图所示:
过点作于点,
由()可得当重合时,
设
,则
,
,,,
解得:
,
设,
解得:
∴.
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.不等式组,的解集在数轴上表示为( )
A. B.
C. D.
3.若a>b,则下列不等式不一定成立的是( )
A.3a>3b B.a﹣1>b﹣2 C.a2>b2 D.1﹣3a<1﹣3b
4.解方程时,去分母结果正确的是( )
A. B.
C. D.
5.电影哪吒之魔童闹海的热映,推动了我国国产动画电影发展,提升了中国文化影响力,下列哪吒图片的变换顺序描述正确的是( )
A.轴对称,平移,旋转 B.旋转,轴对称,平移
C.轴对称,旋转,平移 D.平移,旋转,轴对称
6.明代大数学家程大位著的《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问君多少能完成 ”也就是说:有根短竹,每根短竹可制成毛笔的笔管个或笔套个,怎样安排制作笔管或笔套的短竹数量,使制成的笔管数量与笔套数量正好配套 下列说法正确的是( )
A.设用于制作笔管的短竹数为x根,则可列方程为
B.设用于制作笔管的短竹数为x根,则可列方程为
C.设用于制作笔套的短竹数为y根,则可列方程为
D.设用于制作笔套的短竹数为y根,则可列方程为
7.关于x的一元一次不等式中,m的值应为( )
A.0 B.1 C.2 D.0或2
8.已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
9.如图,已知长方形纸片,点,在边上,点,在边上,分别沿,折叠,使点和点都落在点处,若,则的度数为( )
A. B. C. D.
10.关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.已知方程(m﹣2)x|m|﹣1+8=0是关于x的一元一次方程,则m的值为 .
12.如果,那么x+y+z的值为 .
13.一种运算:x*y=ax+by(a,b为常数),若3*4=2,5*(﹣1)=11,则2*6= .
14.若且abc≠0,则 .
15.若关于x的不等式组仅有5个整数解,则a的取值范围为 .
16.若关于x的一元一次方程的解为x=1,则关于y的一元一次方程ay+b=2y+c的解为y= .
第II卷
华东师大版2024—2025学年七年级下册数学期末考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程组:
(1); (2).
18.(1)解不等式组: (2)解不等式组:
19.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形的位置,,,三角形的周长为30,平移距离为6.
(1)在图中作线段;
(2)求四边形的周长;
(3)求阴影部分的面积.
20.广西平陆运河北起横州市西津水电站库区平塘江口,南止于钦江出海口沙井港航道,在一航道建设中,某渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方.已知5辆大型渣土运输车与2辆小型渣土运输车一次共运输土方吨,6辆大型渣土运输车与4辆小型渣土运输车一次共运输土方吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨
(2)该渣土运输公司决定派出大、小两种型号渣土运输车共辆参与把吨土方全部运走,那么大型渣土运输车至少需要多少辆
21.已知关于x、y的方程满足方程组.
(1)若,求m的值;
(2)若x、y均为非负数,求m的取值范围.
22.在中,过点作交其延长线于点,作的平分线交于点,过点作交于点、交于点.
(1)求证:.
(2)连接,若平分,,求的度数.
23.【阅读】若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”.
【举例】方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“关联方程”.
【问题】
(1)方程是不是不等式组的“关联方程”?请说明理由.
(2)若关于的方程是不等式组的“关联方程”,求的取值范围;
(3)若关于的方程是关于的不等式组的“关联方程”,且此时不等式组有4个整数解,试求的取值范围.
24.已知,直线与交于点,与交于点,点,均不与点重合,平分平分.
(1)如图1,求的度数;
(2)如图2,延长与交于点,过作射线与交于点,且满足.求证:;
(3)如图3,过点作是的外角平分线所在直线,与射线交于点,与交于点.在中,如果有一个角的度数是另一个角的3倍,请直接写出的度数.
25.如图,等腰的对称轴与底边交于点,,,其中、是二元一次方程组的解,,点是边上的一个动点,过点作于点,作于点.
(1)求的面积;
(2)当点在线段上运动时,求的值;
(3)当点在线段的延长线上运动时连接,当时,请补全图形,求此时线段的长.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1—10:DBCDA BDACB
二、填空题
11.【解答】解:由题意可得:|m|﹣1=1且m﹣2≠0,
解得m=﹣2.
故答案为:﹣2.
12.【解答】解:三个方程相加可得:2x+2y+2z=18,
所以x+y+z=9,
故答案为:9
13.【解答】解:∵3*4=2,5*(﹣1)=11,
,
解得:a=2,b=﹣1,
∴2*6=2×2+6×(﹣1)=﹣2,
故答案为:﹣2.
14.【解答】解:设k,
则a=2k,b=3k,c=4k,
所以
=3.
故答案为:3.
15.【解答】解:,
解不等式①得:,
解不等式②得:x≤3,
∵不等式组有5个整数解,即:﹣1,0,1,2,3,
∴,
∴﹣6≤a<﹣3,
故答案为:﹣6≤a<﹣3.
16.【解答】解:,
,
∵关于x的一元一次方程的解为x=1,
∴关于y的一元一次方程ay+b=2y+c的解为:,
故答案为:.
三、解答题
17.(1)解:,
,得,
解得:,
将代入①,得,
解得:,
∴原方程组的解为;
(2)解:,
整理得
由②得,
把③代入①,得,
去括号,得,
解得:,
将代入②,得,
解得:,
∴原方程组的解为.
18.解:(1),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
(1),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
19.(1)解:线段如图所示;
(2)解:∵三角形的周长为30,平移距离为6,
∴,,,
∴四边形的周长
;
(3)解:∵平移得到,
∴,,,
∴,即:梯形的面积等于阴影部分的面积,
∵,
∴梯形的面积为,
∴阴影部分的面积为.
20.(1)解:设一辆大型渣土运输车一次运输土方 x 吨,一辆小型渣土运输车一次运输土方y 吨,
根据题意得 :
解得:.
答:一辆大型渣土运输车一次运输土方吨,一辆小型渣土运输车一次运输土方 5 吨;
(2)解:设需要安排 m 辆大型渣土运输车,则安排辆小型渣土运输车,
根据题意得:,
解得:.
又∵,且为正整数,
∴,
答:至少需要大型渣土车辆.
21.(1)解:,
得:,
,
解得:;
(2)解:
得:,解得,
把代入②得:,解得,
∴原方程组的解为,
、均为非负数,
,,
∴,
解得:.
22.(1)证明:∵平分,
∴,即,
∵,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:由()得:,
∵,
∴,
∴,
∵平分,
∴,
∴.
23.(1)解:方程是不是不等式组的“关联方程”.
理由:由方程,
解得:,
解不等式组,
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:,
∵在的范围内,
∴方程是不等式组的“关联方程”.
(2)解:,
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:,
由方程,
解得:.
∵关于的方程是不等式组的“关联方程”,
,解得:;
(3)解:由关于的方程,
解得:;
,
解不等式①得:,
解不等式②得:,
∴原不等式组的解集为:,
∵不等式组有4个整数解,
∴整数的值为1,2,3,4,
∴,
.
∵关于的方程是关于的不等式组的“关联方程”,
,
解得:,
∴的取值范围:.
24.(1)解:∵,平分,平分,
∴,
∴,
∴;
(2)解:∵平分,平分,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴,
∴;
(3)分情况讨论;①当时,
∵,即,
∴,
∴.
∵是的外角平分线所在的直线,
∴.
∵是的外角,
∴.
∵平分,
∴,
∴.
∵平分,
∴;
当时,
∴.
∵是的外角平分线所在的直线,
∴,
∴.
∵平分,
∴,
∴.
∵平分,
∴.
综上所述,的度数为或.
24.(1)解:解方程组
①②得
解得:,
将代入②得,
解得:
是等腰三角形,对称轴与底边交于点,
∴,
根据等腰三角形三线合一,,
则,,
根据三角形面积公式;
(2)连接,如图所示:
∵,
;
(3)画出点在延长线上,,,如图所示:
过点作于点,
由()可得当重合时,
设
,则
,
,,,
解得:
,
设,
解得:
∴.
同课章节目录
